
KEY DISTRIBUTION BASED ON QUANTUM FOURIER
TRANSFORM
Marius Nagy, Selim G. Akl and Sean Kershaw
School of Computing, Queen’s University, Kingston, Ontario, Canada
Keywords:
Key distribution, protocols, phase shift, quantum Fourier transform, disturbance amplification, eavesdropping
detection.
Abstract:
The data dependencies brought about by the Quantum Fourier Transform can be harnessed to design novel key
distribution protocols with improved performance. Such a protocol maximizes an eavesdropper’s uncertainty
over the information transmitted, while amplifying the disturbance caused by the act of eavesdropping, thus
offering better chances of detecting the intrusion. This is due to the fact that a tested qubit may reveal the
presence of an eavesdropper even if that particular qubit was not ”touched” while in transit.
1 INTRODUCTION
In this paper we explore the feasibility and advantages
offered by a novel approach to quantum key distribu-
tion (QKD). We consider the situation in which Bob
stores the qubits received from Alice until he acquires
more information about how to measure them. This
assumption is motivated by recent advances in lay-
ing the foundation for quantum networks (Cirac et al.,
1997; Blinov et al., 2004) and allows for the creation
of conceptually new protocols for QKD. These new
protocols have the potential to outperform the previ-
ous ones in terms of the total volume of communica-
tion required and (more important, perhaps) the intru-
sion detection rate. The price to pay for these benefits
is a more complex processing of the qubits transmit-
ted.
The remainder of the paper is structured as fol-
lows. Next section is intended as a reference for the
comparison we will make between the new protocol
developed in this paper and the well-known BB84
quantum protocol for key distribution (Bennett and
Brassard, 1984). The section describes a generic
protocol based on phase manipulation, which can be
seen as an abstraction of BB84. Section 3 takes the
idea of phase shifts to a deeper level, as it appears
in the computation of the Quantum Fourier Trans-
form and shows how the interdependencies between
qubits can be exploited to detect eavesdropping activ-
ity in a quantum key distribution protocol. Section
4 demonstrates the improvement in intrusion detec-
tion and security of the novel protocol with respect to
BB84 through a series of simulations. Conclusions
and prospects for future research are presented in sec-
tion 5.
2 RANDOM
π
2
PHASE SHIFT
PROTOCOL
We first describe a BB84 equivalent protocol that we
will use as a building block in designing a QKD
scheme based on the Quantum Fourier Transform.
The main idea of the protocol described in this sec-
tion is to encode each transmitted bit (0 or 1) into the
relative phase between the |0i and |1i components of
a balanced superposition and then encrypt the result-
ing qubit by applying a random phase shift gate, as
depicted in Figure 1. The Hadamard gate provides
the encoding alphabet
“0” 7→
1
√
2
(|0i+ |1i)
“1” 7→
1
√
2
(|0i−|1i)
and the R
θ
gate rotates the relative phase with an angle
θ
R
θ
=
1 0
0 e
iθ
, θ ∈ {0,
π
2
}.
263
Nagy M., G. Akl S. and Kershaw S. (2008).
KEY DISTRIBUTION BASED ON QUANTUM FOURIER TRANSFORM.
In Proceedings of the International Conference on Security and Cryptography, pages 263-269
DOI: 10.5220/0001916802630269
Copyright
c
SciTePress

Eve
BobAlice
H
θ
R
θ
R
H
Figure 1: Schematics of random phase shift protocol for QKD.
Note that R
0
does not affect the state of the qubit onto
which the gate is applied, while R
π/2
rotates the qubit
halfway between the two symbols of the encoding al-
phabet. The gate R
†
θ
denotes the inverse of R
θ
.
Random
π
2
phase shift protocol for QKD
Stage 1: Communication over a quantum channel
Step 1. Alice flips a fair coin to generate a ran-
dom binary sequence that she intends to share
with Bob.
Step 2. For each bit j in the sequence, Alice
chooses , again at random, an angle θ = 0 or
θ = π/2. She then prepares, accordingly, a
qubit in the state |ψi = R
θ
H|ji that she sends
over to Bob.
Step 3. Bob applies the necessary procedures for
safely storing the qubits received from Alice
until the second stage of the protocol, when
he gains knowledge of which qubits have been
phase shifted.
Stage 2: Communication over a public channel
Phase 1. Raw key extraction
Step 1. Alice informs Bob about her choice of
θ for each transmitted bit.
Step 2. Knowing the relative phase shift θ
for each stored qubit |ψi, Bob recovers the
original bit transmitted, by computing |ji =
HR
†
θ
|ψi and then measuring |ji in the normal
computational basis {|0i,|1i}. Following this
procedure, Bob obtains a binary sequence that
should be identical to the one randomly gen-
erated by Alice, provided no eavesdropping or
errors interfered with the quantum transmis-
sion.
Phase 2. Error estimation
Step 1. Over the public channel, Alice and
Bob compare portions of their raw keys to es-
timate the error rate Err. The bits tested are
deleted from their raw keys. If Err = 0 the
remaining bits form their final secret key.
Step 2. If Err > 0, but still sufficiently small,
Alice and Bob may decide to apply privacy
amplification techniques to minimize Eve’s
knowledge about their final secret key. Other-
wise, if Err exceeds a certain threshold, they
discard the whole sequence and start all over
again.
The analogy with BB84 becomes apparent if we
assimilate the encoding alphabet with the horizon-
tal/vertical basis and the π/2 relative phase shift with
the oblique basis. For each qubit Eve decides to tam-
per with, there is a certain chance (25% in our case, as
well as for BB84) that she will be caught. It is impor-
tant to emphasize that this probability is independent
of the actions performed on the other qubits transmit-
ted through the quantum channel. The only way Eve
can be detected is to test one of the qubits she decided
to spy on. In half of the cases, when she is lucky, the
quantum state retransmitted to Bob is identical to the
one intercepted from Alice, so she gains knowledge
of the bit transmitted without any possibility of being
detected. On the other hand, if she gets unlucky, then
her uncertainty about the bit transmitted is total and,
in addition, she disturbs the state of the qubit, intro-
ducing an error rate in Bob’s raw key.
Consequently, Eve could settle for a low level of
eavesdropping, trying to gain only partial knowledge
of the secret key, while minimizing the chances of
being detected. She could even take advantage of
the imperfections in the quantum channel, trying to
hide behind the “noise”. In the next section, we pro-
pose a conceptually new kind of QKD scheme that
aims to maximize Eve’s uncertainty about the bits
she eavesdropped on, even after the public discus-
sion between Alice and Bob, while giving Bob higher
chances of detecting Eve, even for a smaller number
of bits tested. The main idea of the protocol is to prop-
agate the disruption caused by Eve when measuring a
qubit to other qubits in the sequence as well. To this
end we take advantage of the data dependencies in-
troduced by the application of the Quantum Fourier
Transform.
3 QKD SCHEME BASED ON THE
FOURIER TRANSFORM
The Quantum Fourier Transform (QFT) is a very
powerful tool, allowing the design of quantum al-
gorithms that are exponentially faster than their best
SECRYPT 2008 - International Conference on Security and Cryptography
264

classical counterparts, as in the case of Shor’s quan-
tum algorithms for factoring integers and computing
discrete logarithms (Shor, 1997). We show herein that
the QFT and its inverse can also be successfully used
to build quantum key distribution protocols that offer
improved eavesdropping detection rates while max-
imizing the eavesdropper’s uncertainty about the bi-
nary sequence transmitted.
The QFT is a linear operator whose action on any
of the computational basis vectors |0i,|1i,···, |2
n
−1i
associated with an n-qubit register is described by the
following transformation:
|ji −→
1
√
2
n
2
n
−1
∑
k=0
e
2πijk/2
n
|ki, 0 ≤ j ≤2
n
−1. (1)
Equation (1) can be rewritten as a tensor product of
the n qubits involved, as follows:
|j
1
j
2
··· j
n
i −→
(|0i+e
2πi0. j
n
|1i) ⊗···⊗(|0i+ e
2πi0. j
1
j
2
···j
n
|1i)
2
n/2
.
(2)
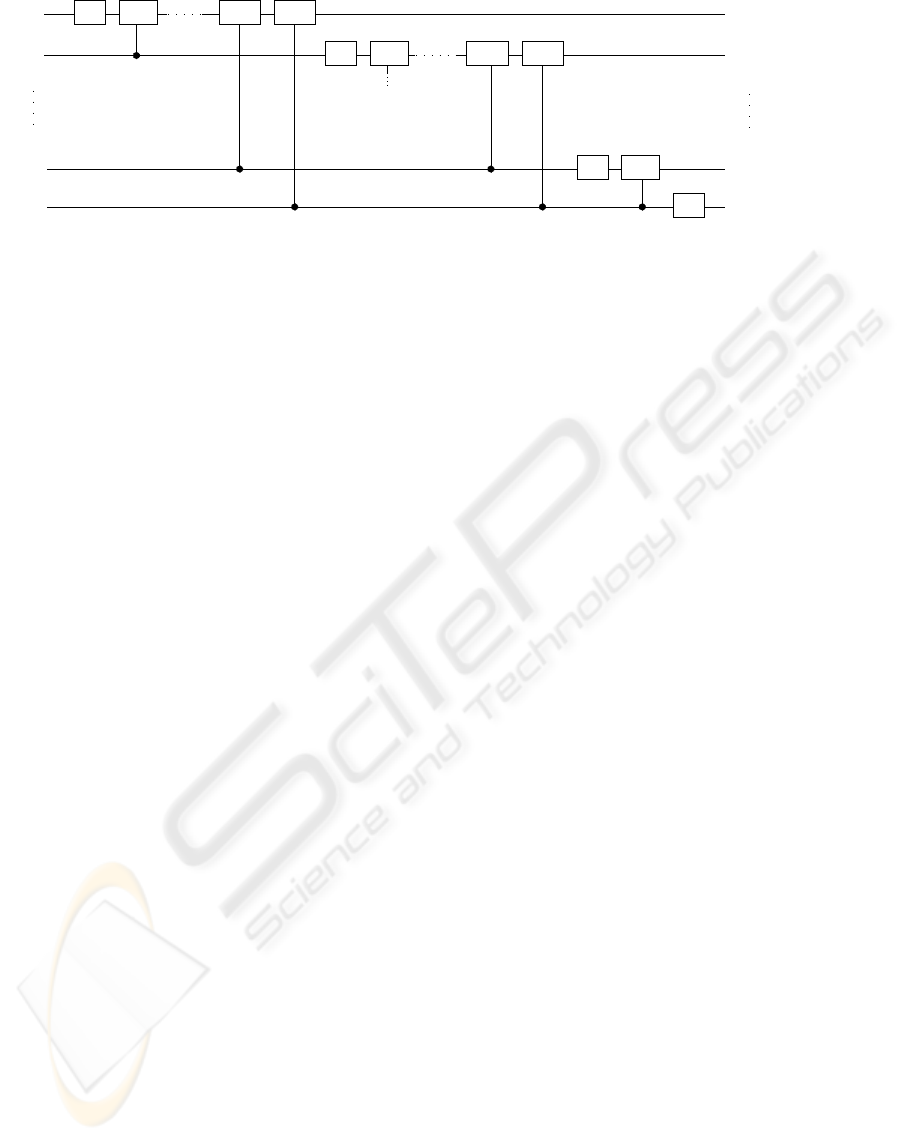
Equation (2) provides the blueprint for devising a cir-
cuit implementing the QFT that requires only Θ(n
2
)
elementary quantum gates (see Figure 2).
In the case of each qubit, the 0 or π phase in-
duced by its own binary value is implemented through
a Hadamard gate. The dependency on the previous
qubits is reflected in the use of controlled phase shifts,
as depicted in Figure 2. Reversing each gate in Fig-
ure 2 gives us an efficient quantum circuit for per-
forming the inverse Fourier transform.
Because of the interdependencies introduced by
the controlled rotations, the procedure must start by
computing |j
n
i and then work its way up to |j
1
i. The
value of |j
n
i is needed in the computation of |j
n−1
i.
Both |j
n
i and |j
n−1
i are required in order to obtain
|j
n−2
i. This continues in the same manner, until fi-
nally, the values of all the higher rank bits are used to
determine |j
1
i precisely.
This fixed order of execution can be exploited to
design secure QKD schemes. The protocol that we
describe in the following can be seen as a general-
ization of the random π/2 phase shift protocol, both
relying on encapsulating information in the relative
phase between the two components in a superposi-
tion. However, the Fourier transform brings into play
the rank of a qubit in the sequence, thus giving a con-
text to each qubit transmitted.
Employing the Fourier transform instead of the ran-
dom π/2 phase shift as the encryption method does
not alter the main structure of the protocol, so we will
just point out the differences relative to the descrip-
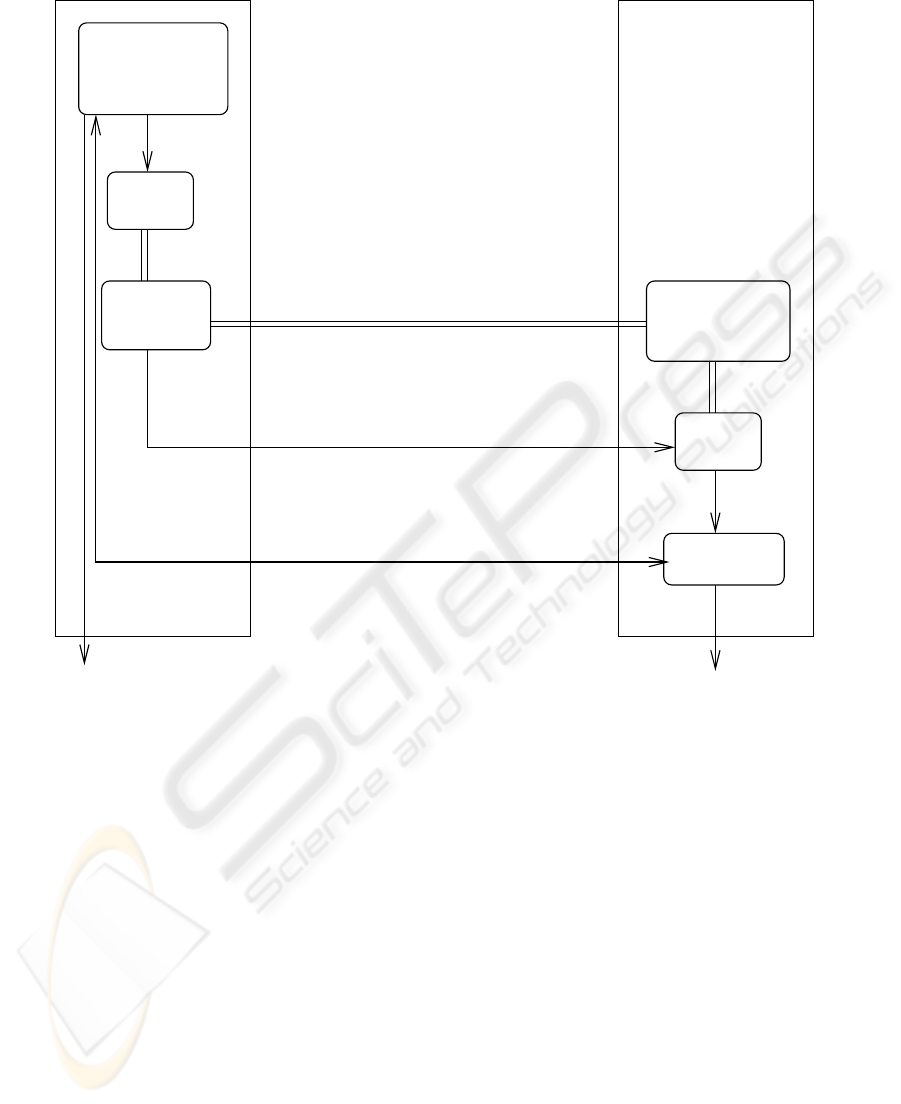
tion we provided in the previous section. Figure 3
gives a pictorial representation of the entire protocol,
with time flowing downwards.
In step 2 of the quantum communication stage, Al-
ice applies the QFT to the binary sequence generated
in the previous step, by passing it through the quan-
tum circuit depicted in Figure 2. Then, she scrambles
the resulting qubit sequence by choosing an arbitrary
permutation of the qubits and sends them to Bob.
In the second stage of the protocol (involvingclas-
sical communication), Alice informs Bob of the cor-
rect order in which he must place the received qubits
(in other words, the rank of each qubit is disclosed).
Consequently,the raw keyextraction step can proceed
with Bob applying the inverse Fourier transform to
the properly re-arranged qubit sequence. In the ab-
sence of any eavesdropping or transmission errors,
Bob must end up with the same bit sequence that Al-
ice randomly produced at the outset of the protocol.
When Eve decides to spy on an arbitrary qubit in
the sequence, she doesn’t know its rank and is there-
fore ignorant of the influence exerted on it by the pre-
vious qubits in the ordered sequence. Without ac-
cess to this additional information (the qubit’s con-
text), Eve can have no confidencein the outcome of an
eventual measurement in the Hadamard basis pointing
to a 0 or a 1.
3.1 An Example
Suppose that the bit string that Alice wants to convey
to Bob is 10011010, so that j
1
= 1 and j
8
= 0. Con-
sider what happens if Eve intercepts the qubit of rank
6 and measures it in the Hadamard basis. Since its
state is
|0i+ e
2πi0.010
|1i = |0i+ e
π
2
i
|1i, (3)
exactly halfway between |0i and |1i (relative phase
π/2), there is an equal probability for either outcome
to be realized. Consequently, even after learning its
context, Eve’s uncertainty over this bit is total. Fol-
lowing her measurement, Eve can either send H|0i or
H|1i to Bob. In any case, Bob will undo the π/2 rota-
tion supposedly caused by j
7
= 1, therefore having a
50% chance of detecting Eve, provided he and Alice
choose to test bit j
6
. But if Bob measures bit j
6
as 1,
then the error introduced by Eve’s action is still de-
tectable, even if the qubit whose state she disturbed is
not checked by Alice and Bob. Thus, when applying
the inverse Fourier transform on the qubit of rank 5,
its quantum state becomes
|0i+ e
(π+
π
4
−
π
4
−
π
2
)i
|1i (4)
and in 50% of the cases Alice and Bob will discover
a mismatch in their values for this bit. An erroneous
KEY DISTRIBUTION BASED ON QUANTUM FOURIER TRANSFORM
265
R
2
H
2
RH
n-1
R
n-2
R
2
RH
n
R
n-1
RH
π2
|0> + e |1>
2
i0.j ... j
n
π2
|0> + e |1>
|0> + e |1>
π2 i0.j ... j
1 n
n
|j >
|j >
n-1
2
|j >
|j >
1
n-1
n
i0.jπ2
|0> + e |1>
n
i0.j j
Figure 2: Quantum circuit performing the discrete Fourier transform.
bit j
6
will continue to influence the outcome of the
following bits, up to j
1
. The strength of this influence
decreases with the rank and probably becomes negli-
gible in a few steps. Nevertheless, if the error in j
6
propagates to one of its neighbors, then this bit acts
as a new source of error, creating the mechanism for
the initial disturbance to propagate indefinitely. So,
unlike other QKD schemes, in this case, eavesdrop-
ping on one qubit has the potential to introduce a large
number of errors. In general, for an arbitrary qubit
of rank k (0 < k ≤ n), the relative phase shift caused
by errors in the previous bits (from n to k + 1) varies
between 0 and
∑
n−k
i=1
π/2
i
, as the errors induced may
interfere with each other, adding up or canceling out.
Since Eve’s uncertainty over an observed value is
based on her ignorance about the context involved, it
appears that the weak spot of the protocol lies in the
high rank qubits. The highest rank qubit, for instance,
is context-free (having no predecessors), so Eve can
be certain of its value, provided she has performed
a measurement on it. But because she doesn’t know
the ranks of the qubits transmitted during the quantum
communication stage, she must eavesdrop on many
qubits to increase her chances of learning the value
of j
n
. This, in turn, will cause more disturbance and
therefore increase the risk of being detected.
In our example, by learning that the value of j
8
equals 0, Eve also becomes aware that j
8
has no influ-
ence on j
7
, so her measurement on j
7
(if performed)
must have yielded its true value. However, since
j
7
= 1, there is an equal probability that a hypothetical
measurement on j
6
has revealed the correct or incor-
rect value. For an arbitrary bit string j
1
··· j
n
, Eve can
end up knowing the values of the last k bits, where
j
n−k+1
= 1 and j
n−k+2
,··· , j
n−1
, j
n
are all zeroes, as-
suming that she performed all the necessary measure-
ments on the qubits in transit. In practice, since the
binary sequence transmitted is chosen at random, the
probability of it ending in more than two or three con-
secutive zeroes is very low.
One immediate solution is for Alice and Bob to
discard those bits from their raw keys. Alterna-
tively, the protocol described above, and based on the
Fourier transform, could be combined with the ran-
dom π/2 phase shift protocol presented in the previ-
ous section. In this way, each qubit may get an ad-
ditional π/2 relative phase shift, increasing Eve’s un-
certainty about the trailing bits in the sequence while
maintaining the uncertainty level for the others.
4 SIMULATIONS
In order to better assess the improvement in perfor-
mance brought by the QFT-based protocol with re-
spect to the traditional BB84 protocol, a series of sim-
ulations for various input parameters were performed.
To ensure a fair comparison between the two pro-
tocols, we assumed that Bob has knowledge of the
encoding bases chosen by Alice, such that no qubits
are discarded in the BB84 protocol because of a mis-
match between the encoding and decoding bases. A
series of 1000 simulations were performed for each
possible configuration allowed by varying the follow-
ing input parameters:
- total number of qubits transmitted (128, 256, 512),
- percentage of qubits eavesdropped on by Eve (10,
25, 50),
- percentage of qubits checked for eavesdropping by
Alice and Bob (10, 25, 50).
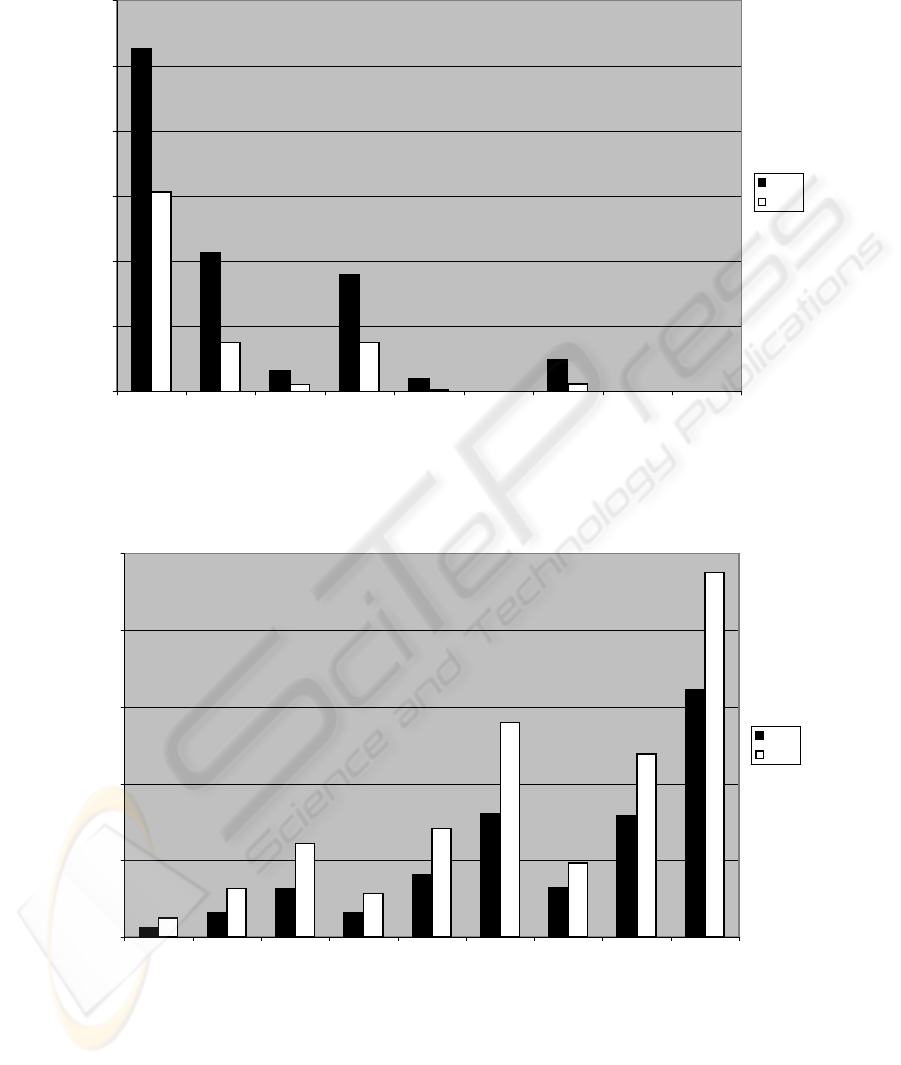
Figure 4 shows the results in terms of the number of
times Eve managed to remain undetected during each
batch of 1000 simulations of the two protocols. For
the same number of qubits eavesdropped on and the
same number of qubits checked, the QFT-based pro-
tocol consistently outperforms BB84 because the er-
rors introduced by eavesdropping propagate to other
qubits as well and thus Eve may get caught even if the
bit checked was not eavesdropped on. We can see that
the improvement is bigger for lower levels of eaves-
dropping and/or fewer bits checked.
Figure 5, on the other hand, shows the average
number of qubits (out of 256) that were detected as
SECRYPT 2008 - International Conference on Security and Cryptography
266
generate
randomly
QFT
scramble
qubits
raw key
qubit
storage
IQFT
Alice Bob
<
<
>
information about the rank of each qubit
test some bits for eavesdropping
final key final key
quantum channel
key
Figure 3: Schematics of a quantum key distribution protocol using the quantum Fourier transform (QFT) and its inverse
(IQFT) as encoding and decoding algorithms. This is the first protocol that allows the detection of an eavesdropper even if the
qubit tested was not “disturbed” while in transit.
corrupted by Eve in each 1000-trial batch. The im-
provement in performance in favor of the QFT-based
protocol is evident for each combination of input vari-
ables.
5 CONCLUSIONS
In this paper, we have addressed the quantum key dis-
tribution problem from the novel perspective allowed
by the possibility of temporarily storing the qubits re-
ceived through the quantum communications chan-
nel during a protocol. This assumption is well mo-
tivated by the progress achieved in quantum networks
research. The immediate advantage is a significant
decrease in the volume of quantum and classical com-
munication required between the two parties. In ad-
dition, under the new assumption, conceptually new
QKD schemes can be designed, with improved effi-
ciency, security and eavesdropping detection.
One idea that we propose in this paper is to bring
into play the dependencies between qubits created by
the Quantum Fourier Transform in order to obtain
a protocol with superior performance. When com-
pared with existing QKD schemes, the protocol using
the QFT offer better eavesdropping detection rates by
propagating the disruption caused to one qubit to the
following qubits in the sequence. This makes the pro-
tocol more efficient in terms of the number of bits
that have to be tested in order to achieve a certain
level of security. Also, the lack of knowledge over
a qubit’s context, at the time of eavesdropping, max-
imizes Eve’s uncertainty about the information en-
coded within its quantum state, thus making the pro-
tocol more secure.
These benefits come at the cost of a more complex
KEY DISTRIBUTION BASED ON QUANTUM FOURIER TRANSFORM
267
256 Bits
525
213
32
178
19
0
48
0 0
306
75
10
75
2
0
11
0 0
0
100
200
300
400
500
600
10,10 10,25 10,50 25,10 25,25 25,50 50,10 50,25 50,50
(% eved, % checked)
# times Eve undetected in 1000
BB84
QFT
Figure 4: A comparison between the QFT-based and the BB84 protocol, in terms of the number of times Eve escapes detection
in 1000 trials, for various percentages of bits eavesdropped on and checked.
256 Bits
0.66
1.60
3.16
1.63
4.05
8.04
3.22
7.89
16.09
1.24
3.17
6.12
2.83
7.09
13.97
4.83
11.93
23.77
0.00
5.00
10.00
15.00
20.00
25.00
10,10 10,25 10,50 25,10 25,25 25,50 50,10 50,25 50,50
(% bits eaved., % bits checked)
Avg # bits, Eve detected
BB84
QFT
Figure 5: A comparison between the QFT-based and the BB84 protocol, in terms of the average number of corrupt bits
detected in 1000 trials, for various percentages of bits eavesdropped on and checked.
processing required at both ends of the link. How-
ever, the computational power assumed to be avail-
able for Alice and Bob is not that of a quantum com-
puter. Alice and Bob need only to be able to perform
Hadamard and phase shift rotations of single-qubit
quantum states. Parallel processing can also be ap-
plied in order to avoid decoherence (Nagy and Akl,
2006).
The protocol for QKD developed in this paper
demonstrates that the QFT is a versatile tool, with im-
SECRYPT 2008 - International Conference on Security and Cryptography
268

portant applications not only in quantum algorithms,
butalso in quantumcryptography. It allows for the de-
sign of new QKD schemes with clear advantages over
the existing ones, especially for low levels of eaves-
dropping. Furthermore, the results obtained herein
suggest that the role of QFT in the general area of
data security is much more important than previously
believed.
REFERENCES
Bennett, C. H. and Brassard, G. (1984). Quantum cryp-
tography: Public key distribution and coin tossing.
In Proceedings of IEEE International Conference on
Computers, Systems and Signal Processing, pages
175–179, IEEE, New York. Bangalore, India, Decem-
ber 1984.
Blinov, B. B., Moehring, D. L., Duan, L.-M., and Mon-
roe, C. (2004). Observation of entanglement between
a single trapped atom and a single photon. Nature,
428:153–157.
Cirac, I., Zoller, P., Kimble, H. J., and Mabuchi, H. (1997).
Quantum state transfer and entanglement distribution
among distant nodes in a quantum network. Physical
Review Letters, 78(16):3221–3224.
Nagy, M. and Akl, S. G. (2006). Coping with Decoherence:
Parallelizing the Quantum Fourier Transform. In 19th
International Conference on Parallel and Distributed
Computing Systems, pages 108–113, San Francisco,
California.
Shor, P. W. (1997). Polynomial-time algorithms for prime
factorization and discrete logarithms on a quantum
computer. Special issue on Quantum Computation of
the SIAM Journal on Computing, 26(5):1484–1509.
KEY DISTRIBUTION BASED ON QUANTUM FOURIER TRANSFORM
269
