CONSTRAINT PROGRAMMING CAN HELP ANTS SOLVING

HIGHLY CONSTRAINTED COMBINATORIAL PROBLEMS

Broderick Crawford

Pontiﬁcia Universidad Cat´olica de Valpara´ıso, Universidad T´ecnica Federico Santa Mar´ıa, Chile

Carlos Castro, Eric Monfroy

Universidad T´ecnica Federico Santa Mar´ıa, University of Nantes, France

Keywords:

Ant Colony Optimization (ACO), Constraint Programming (CP), Constraint Propagation, Arc Consistency

(AC), Set Partitioning Problem (SPP).

Abstract:

In this paper, we focus on the resolution of Set Partitioning Problem. We try to solve it with Ant Colony

Optimization algorithms and Hybridizations of Ant Colony Optimization with Constraint Programming tech-

niques. We recognize the difﬁculties of pure Ant Algorithms solving strongly constrained problems. There-

fore, we explore the addition of Constraint Programming mechanisms in the construction phase of the ants so

they can complete their solutions. Computational results solving some test instances are presented showing

the advantages to use this kind of hybridization.

1 INTRODUCTION

There exist some problems for which the effective-

ness of Ant Colony Optimization (ACO) is lim-

ited, among them the strongly constrained problems.

Those are problems for which neighbourhoods con-

tain few solutions, or none at all, and local search

has a very limited use. Probably, the most signiﬁ-

cant of those problems is the Set Partitioning Problem

(SPP) and a direct implementation of the basic ACO

framework is unable of obtaining feasible solutions

for many SPP standard tested instances (Maniezzo

and Milandri, 2002). The best performing meta-

heuristic for SPP is a genetic algorithm due to Chu

and Beasley (Chu and Beasley, 1998; Beasley and

Chu, 1996). There already exists some ﬁrst ap-

proaches applying ACO to the Set Covering Problem

(SCP) (Alexandrov and Kochetov, 2000; Leguizam´on

and Michalewicz, 1999). More recent works (Hadji

et al., 2000; Lessing et al., 2004; Gandibleux et al.,

2004) apply Ant Systems to the SCP and related prob-

lems using techniques to remove redundant columns

and local search to improve solutions. In this pa-

per, we explore the addition of a lookahead mecha-

nism to the two main ACO algorithms: Ant System

(AS) and Ant Colony System (ACS). Trying to solve

larger instances of SPP with AS or ACS implemen-

tations derives in a lot of unfeasible labelling of vari-

ables and the ants can not obtain complete solutions

using the classic transition rule when they move in

their neighbourhood. We propose the addition of a

lookahead mechanism from Constraint Programming

(CP) in the construction phase of ACO thus only fea-

sible partial solutions are generated. The lookahead

mechanism allows the incorporation of information

about the instantiation of variables after the current

decision (Michel and Middendorf, 1998; Gagne et al.,

2001).

2 PROBLEM DESCRIPTION

The Set Partitioning Problem is the NP-complete

problem of partitioning a given set into mutually in-

dependent subsets while minimizing a cost function

deﬁned as the sum of the costs associated to each of

the eligible subsets. In the SPP matrix formulation

we are given a m× n matrix A = (a

) in which all the

matrix elements are either zero or one. Additionally,

each column is given a non-negative cost c

. We say

that a column j can cover a row i if a

= 1. Let J de-

notes the set of the columns and x

a binary variable

which is one if column j is chosen and zero otherwise.

The SPP can be deﬁned formally as follows:

380

Crawford B., Castro C. and Monfroy E. (2008).

CONSTRAINT PROGRAMMING CAN HELP ANTS SOLVING HIGHLY CONSTRAINTED COMBINATORIAL PROBLEMS.

In Proceedings of the Third International Conference on Software and Data Technologies - PL/DPS/KE, pages 380-383

DOI: 10.5220/0001892403800383

 SciTePress

Minimize f(x) =

∑

j=1

(1)

Sub ject to

∑

j=1

= 1; ∀i = 1,...,m (2)

3 ANT COLONY OPTIMIZATION

In this section, we brieﬂy present ACO algorithms

and give a description of their use to solve SPP. More

details about ACO algorithmscan be foundin (Dorigo

et al., 1999; Dorigo and Gambardella, 1997). The ba-

sic idea of ACO algorithms comes from the capabil-

ity of real ants to ﬁnd shortest paths between the nest

and food source. From a Combinatorial Optimization

point of view, the ants are looking for good solutions.

ACO can be applied in a very straightforward way

to SPP. The columns are chosen as the solution com-

ponents and have associated a cost and a pheromone

trail (Dorigo and Stutzle, 2004). Each column can be

visited by an ant only once and then a ﬁnal solution

has to cover all rows. A walk of an ant over the graph

representation corresponds to the iterative addition of

columns to the partial solution obtained so far. Each

ant starts with an empty solution and adds columns

until a cover is completed. A pheromone trail τ

and

a heuristic information η

are associated to each el-

igible column j. A column to be added is chosen

with a probability that depends of pheromonetrail and

the heuristic information. The most common form of

the ACO decision policy (Transition Rule Probabil-

ity) when ants work with components is:

(t) =

∗ η

∑

l/∈S

[η

]

if j /∈ S

(3)

where S

is the partial solution of the ant k. The

β parameter controls how important is η in the prob-

abilistic decision (Dorigo and Stutzle, 2004; Lessing

et al., 2004). In this work the pheromonetrail τ

is put

on the problems component (each eligible column j)

and we use a dynamic heuristic information deﬁned

as η

, where e

is the so called cover value,

that is, the number of additional rows covered when

adding column j to the current partial solution, and c

is the cost of column j. We use two instances of ACO:

Ant System (AS) and Ant Colony System (ACS) al-

gorithms (Dorigo and Stutzle, 2004). Trying to solve

larger instances of SPP with the original AS or ACS

implementation derives in a lot of unfeasible labelling

of variables, and the ants can not obtain complete so-

lutions. A direct implementation of the basic ACO

framework is incapable of obtaining feasible solution

for many SPP instances. Then we explore the addition

of a lookahead mechanism in the construction phase

of ACO thus only feasible solutions are generated.

4 CONSTRAINT

PROGRAMMING

The two basic techniques of Constraint Programming

to solve combinatorial problems are Constraint Prop-

agation and Constraint Distribution (Apt, 2003). Con-

straint Propagation embeds any reasoning which con-

sists in explicitly forbidding values or combinations

of values for some variables of a problem because a

given subset of its constraints cannot be satisﬁed oth-

erwise. The algorithm proceeds as follows: when a

value is assigned to a variable, the algorithm recom-

putes the variable domains and assigned values of all

its dependent variables (variable that belongs to the

same constraint). This process continues recursively

until no more changes can be done. It causes the algo-

rithm to recompute the values for further downstream

variables. In the case of binary variables the con-

straint propagation works very fast in strongly con-

strained problems like SPP.

The problem cannot be solved using Constraint

Propagation alone, Constraint Distribution or Search

is required to reduce the search space until Constraint

Propagation is able to determine the solution. Con-

straint Distribution splits a problem into complemen-

tary cases once Constraint Propagation cannot ad-

vance further. By iterating propagation and distribu-

tion, propagation will eventually determine the solu-

tions of a problem (Apt, 2003).

5 INTEGRATING ACO WITH CP

Recently, some efforts have been done in order to in-

tegrate Constraint Programming techniques to ACO

algorithms (Meyer and Ernst, 2004; Focacci et al.,

2002). In this work, ACO useCP in the variableselec-

tion (when adding columns to partial solution). The

CP algorithm used in this paper is Forward Check-

ing with Backtracking. The algorithm is a combina-

tion of Arc Consistency Technique and Chronological

Backtracking (Dechter and Frost, 2002). It performs

Arc Consistency between pairs of a not yet instanti-

ated variable and an instantiated variable, i.e., when a

value is assigned to the current variable, any value in

CONSTRAINT PROGRAMMING CAN HELP ANTS SOLVING HIGHLY CONSTRAINTED COMBINATORIAL

PROBLEMS

381

the domain of a future variable which conﬂicts with

this assignment is removed from the domain. For-

ward Checking search procedure guarantees that at

each step of the search, all the constraints between

already assigned variables and not yet assigned vari-

ables are arc consistency. This reduces the search tree

and the overall amount of computational work done.

The cost is that Arc consistency enforcing always in-

creases the information available on each variable la-

belling.

6 EXPERIMENTAL RESULTS

Table 3 presents the results when adding Forward

Checking to the basic ACO algorithmsfor solving test

instances taken from the OR-Library (Beasley, 1990).

Table 1 presents the problem code, the number of

rows (constraints), the number of columns (decision

variables), the best known cost value for each instance

(IP optimal), and the density (percentage of ones in

the constraint matrix) respectively. Table 2 presents

the results obtained by better performing metaheuris-

tics with respect to SPP, Genetic Algorithm of Chu

and Beasley (Chu and Beasley, 1998), Genetic Algo-

rithm of Levine et al. (Levine, 1994) and the most

recent algorithm by Kotecha et al. (Kotecha et al.,

2004). An entry of ”X” in the table means no feasi-

ble solution was found. The algorithms have been run

with the following parameters settings: inﬂuence of

pheromone (alpha)=1.0, inﬂuence of heuristic infor-

mation (beta)=0.5 and evaporation rate (rho)=0.4 as

suggested in (Leguizam´on and Michalewicz, 1999;

Lessing et al., 2004; Dorigo and Stutzle, 2004). The

number of ants has been set to 120 and the maximum

number of iterations to 160, so that the numberof gen-

erated candidate solutions is limited to 19.200. For

ACS the list size was 500 and Qo=0.5. Algorithms

were implemented using ANSI C, GCC 3.3.6, under

Microsoft Windows XP Professional version 2002.

The effectiveness of Constraint Programming is

showed to solve SPP, because the SPP is so strongly

constrained the stochastic behaviour of ACO can be

improved with lookahead techniques in the construc-

tion phase, so that almost only feasible partial solu-

tions are induced. In the original ACO implemen-

tation the SPP solving derives in a lot of unfeasible

labelling of variables, and the ants can not complete

solutions. With respect to the computational results

this is not surprising, because ACO metaheuristics

are general purpose tools that will usually be outper-

formed when customized algorithms for a problem

exist.

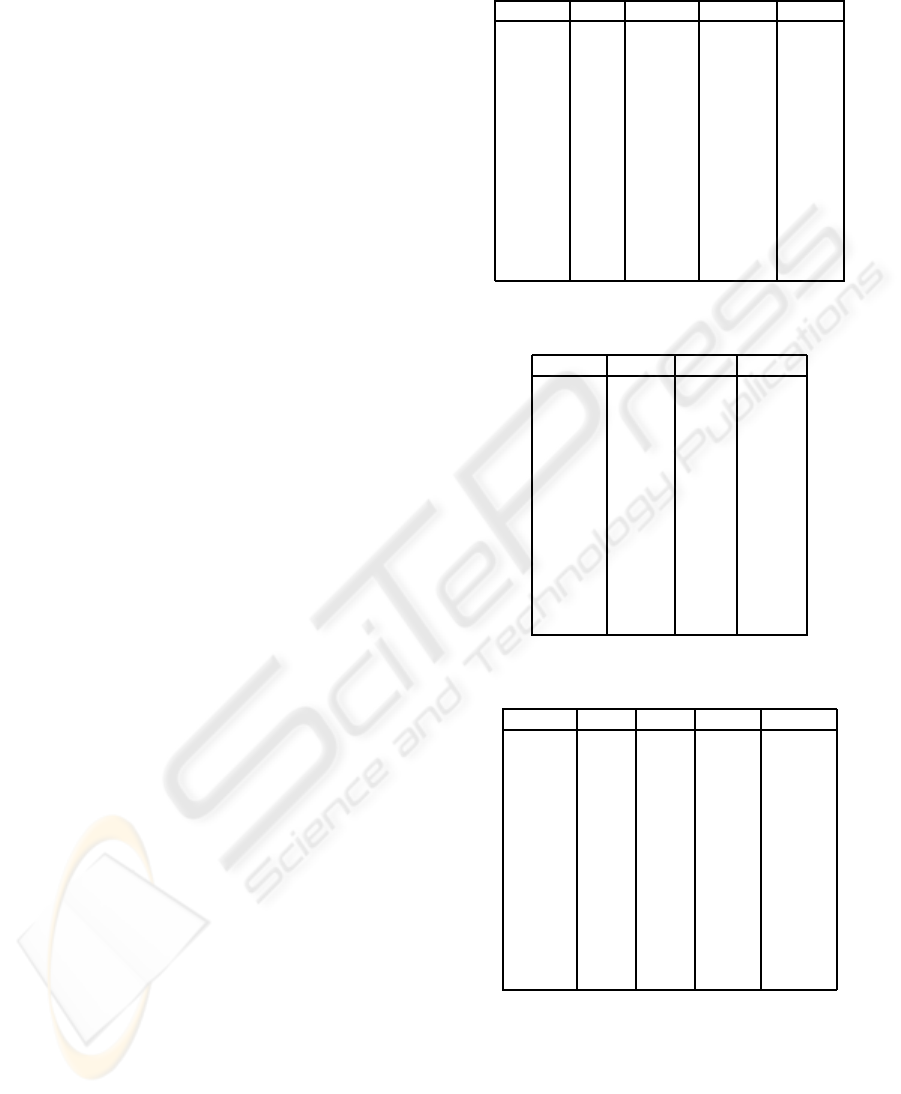
Table 1: Benchmark instances.

Problem Rows Columns Optimum Density

sppnw06 50 6774 7810 18.17

sppnw08 24 434 35894 22.39

sppnw09 40 3103 67760 16.20

sppnw10 24 853 68271 21.18

sppnw12 27 626 14118 20.00

sppnw15 31 467 67743 19.55

sppnw19 40 2879 10898 21.88

sppnw23 19 711 12534 24.80

sppnw26 23 771 6796 23.77

sppnw32 19 294 14877 24.29

sppnw34 20 899 10488 28.06

sppnw39 25 677 10080 26.55

sppnw41 17 197 11307 22.10

Table 2: Better performing Metaheuristics results.

Problem Beasley Levine Kotecha

sppnw06 7810 - -

sppnw08 35894 37078 36068

sppnw09 67760 - -

sppnw10 68271 X 68271

sppnw12 14118 15110 14474

sppnw15 67743 - -

sppnw19 10898 11060 11944

sppnw23 12534 12534 12534

sppnw26 6796 6796 6804

sppnw32 14877 14877 14877

sppnw34 10488 10488 10488

sppnw39 10080 10080 10080

sppnw41 11307 11307 11307

Table 3: ACO and ACO+FC results.

Problem AS ACS AS+FC ACS+FC

sppnw06 9200 9788 8160 8038

sppnw08 X X 35894 36682

sppnw09 70462 X 70222 69332

sppnw10 X X X X

sppnw12 15406 16060 14466 14252

sppnw15 67755 67746 67743 67743

sppnw19 11678 12350 11060 11858

sppnw23 14304 14604 13932 12880

sppnw26 6976 6956 6880 6880

sppnw32 14877 14886 14877 14877

sppnw34 13341 11289 10713 10797

sppnw39 11670 10758 11322 10545

sppnw41 11307 11307 11307 11307

7 CONCLUSIONS

Our main contribution is the study of the combina-

tion of Constraint Programming and Ant Colony Op-

timization solving benchmarks of the Airline Crew

Pairing Problem formulated as a Set Partitioning

Problem. The main conclusion from this work is

ICSOFT 2008 - International Conference on Software and Data Technologies

382

that we can improve ACO with CP. Computational

results also indicated that our hybridization is capa-

ble of generating optimal or near optimal solutions

for many problems. The concept of Arc Consistency

plays an essential role in Constraint Programming as

a problem simpliﬁcation operation and as a tree prun-

ing technique during search through the detection of

local inconsistencies among the uninstantiated vari-

ables. We have shown that it is possible to add Arc

Consistency to any ACO algorithms and the compu-

tational results conﬁrm that the performance of ACO

can be improved with this type of hybridisation. Any-

way, a complexity analysis should be done in order

to evaluate the cost we are adding with this kind of

integration. We strongly believe that this kind of inte-

gration between complete and incomplete techniques

should be studied deeply.

Future versions of the algorithm will study the

pheromone treatment representation and the incorpo-

ration of available techniques in order to reduce the

input problem (Pre Processing) and improve the so-

lutions given by the ants (Post Processing). The ants

solutions may contain expensive components which

can be eliminated by a ﬁne tuning heuristic after the

solution, then we will explore Post Processing proce-

dures, which consists in the identiﬁcation and replace-

ment of the columns of the ACO solution in each it-

eration by more effective columns. Besides, the ants

solutions can be improvedby other local search meth-

ods like Hill Climbing, Simulated Annealing or Tabu

Search.

REFERENCES

Alexandrov, D. and Kochetov, Y. (2000). Behavior of the

ant colony algorithm for the set covering problem. In

Proc. of Symp. Operations Research, pages 255–260.

Springer Verlag.

Apt, K. R. (2003). Principles of Constraint Programming.

Cambridge University Press.

Beasley, J. E. (1990). Or-library:distributing test problem

by electronic mail. Journal of Operational Research

Society, 41(11):1069–1072.

Beasley, J. E. and Chu, P. C. (1996). A genetic algorithm

for the set covering problem. European Journal of

Operational Research, 94(2):392–404.

Chu, P. C. and Beasley, J. E. (1998). Constraint handling in

genetic algorithms: the set partitoning problem. Jour-

nal of Heuristics, 4:323–357.

Dechter, R. and Frost, D. (2002). Backjump-based back-

tracking for constraint satisfaction problems. Artiﬁcial

Intelligence, 136:147–188.

Dorigo, M., Birattari, M., Blum, C., Gambardella, L. M.,

Mondada, F., and St¨utzle, T., editors (2004). Ant

Colony Optimization and Swarm Intelligence, 4th In-

ternational Workshop, ANTS 2004, Brussels, Belgium,

September 5 - 8, 2004, Proceedings, volume 3172 of

Lecture Notes in Computer Science. Springer.

Dorigo, M., Caro, G. D., and Gambardella, L. M. (1999).

Ant algorithms for discrete optimization. Artiﬁcial

Life, 5:137–172.

Dorigo, M. and Gambardella, L. M. (1997). Ant colony sys-

tem: A cooperative learning approach to the traveling

salesman problem. IEEE Transactions on Evolution-

ary Computation, 1(1):53–66.

Dorigo, M. and Stutzle, T. (2004). Ant Colony Optimiza-

tion. MIT Press, USA.

Focacci, F., Laburthe, F., and Lodi, A. (2002). Local search

and constraint programming. In Handbook of meta-

heuristics. Kluwer.

Gagne, C., Gravel, M., and Price, W. (2001). A look-

ahead addition to the ant colony optimization meta-

heuristic and its application to an industrial schedul-

ing problem. In et al., J. S., editor, Proceedings

of the fourth Metaheuristics International Conference

MIC’01, pages 79–84.

Gandibleux, X., Delorme, X., and T’Kindt, V. (2004). An

ant colony optimisation algorithm for the set packing

problem. In (Dorigo et al., 2004), pages 49–60.

Hadji, R., Rahoual, M., Talbi, E., and Bachelet, V. (2000).

Ant colonies for the set covering problem. In et al.,

M. D., editor, ANTS 2000, pages 63–66.

Kotecha, K., Sanghani, G., and Gambhava, N. (2004). Ge-

netic algorithm for airline crew scheduling problem

using cost-based uniform crossover. In Second Asian

Applied Computing Conference, AACC 2004, volume

3285 of Lecture Notes in Artiﬁcial Intelligence, pages

84–91, Kathmandu, Nepal. Springer.

Leguizam´on, G. and Michalewicz, Z. (1999). A new ver-

sion of ant system for subset problems. In Congress

on Evolutionary Computation, CEC’99, pages 1459–

1464, Piscataway, NJ, USA. IEEE Press.

Lessing, L., Dumitrescu, I., and St¨utzle, T. (2004). A com-

parison between aco algorithms for the set covering

problem. In (Dorigo et al., 2004), pages 1–12.

Levine, D. (1994). A parallel genetic algorithm for the

set partitioning problem. Technical Report ANL-

94/23 Argonne National Laboratory. Available at

http://citeseer.ist.psu.edu/levine94parallel.html.

Maniezzo, V. and Milandri, M. (2002). An ant-based

framework for very strongly constrained problems. In

Dorigo, M., Caro, G. D., and Sampels, M., editors, Ant

Algorithms, volume 2463 of Lecture Notes in Com-

puter Science, pages 222–227. Springer.

Meyer, B. and Ernst, A. (2004). Integrating aco and con-

straint propagation. In (Dorigo et al., 2004), pages

166–177.

Michel, R. and Middendorf, M. (1998). An island model

based ant system with lookahead for the shortest su-

persequence problem. In Lecture notes in Computer

Science, Springer Verlag, volume 1498, pages 692–

701.

CONSTRAINT PROGRAMMING CAN HELP ANTS SOLVING HIGHLY CONSTRAINTED COMBINATORIAL

PROBLEMS

383