A Petri Net based Approach to Modelling Resource
Constrained Interorganizational Workflows
Oana Prisecaru
Faculty of Computer Science, ”Al. I. Cuza” University
Gen. Berthlot St, No 16, 740083 Iasi, Romania
Abstract. Interorganizational workflows represent a technique that offers com-
panies a solution for managing business processes that involve more than one
organization. In this paper, an interorganizational workflow will be modelled
using a special class of nested Petri nets, resource constrained interorganiza-
tional workflow nets. This approach will allow the specification of the partici-
pating workflows and of the communication structure between them, permitting
a clear distinction between these components. In our model, the resources from
one workflow can be represented explicitly and shared with other component
workflows.
1 Introduction
A workflow is the automation of a business process that takes place inside one organi-
zation. A workflow is structured into several perspectives, among which we mention:
the process perspective - specifies which tasks need to be executed and in what order;
the resource perspective - specifies the resources in the organization and the existing
roles (resource classes based on organizational or functional aspects). Due to the rise
of virtual organizations, electronic commerce and international companies, many ex-
istent business processes involve more than one organization. These workflows , dis-
tributed over a number of different organizations, are referred to as interorganizational
workflows. There have been developed several specification languages for interorgani-
zational workflows, based on XML and Web services: WSFL, BPEL4WS, XLANG,
WSCL, etc ([8]). These languages lack formal semantics and analytical power (they
cannot be used to study behavioural properties of interorganizational workflows). In
order to solve these problems, several formalisms have been proposed for specifying
interorganizational workflows: Communicating Finite Automata ([6]), Category the-
ory ([7]), Process algebra and Petri nets. Petri nets represent a well-known formal
method, successfully used as a modelling technique for workflows (see [1,2]), due to
their graphical representation, their formal semantics and expressiveness. Also, there
are many analysis techniques and tools used for investigating the properties of Petri
nets. Petri nets have also been used for modelling interorganizational workflows: in [3],
IOWF-nets are defined for modelling loosely coupled interorganizational workflows.
Prisecaru O. (2008).
A Petri Net based Approach to Modelling Resource Constrained Interorganizational Workflows.
In Proceedings of the 6th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages 29-38
DOI: 10.5220/0001736700290038
Copyright
c
 SciTePress

[15] describes a XML-based language, called XRL, for the specification of interorgani-
zational workflows. XRL semantic is expressed in terms of Petri nets. The approach in
[5] uses Documentary Petri Nets, a variant of high-level Petri nets, to model and enact
trade procedures. The P2P approach from [4], based on Petri nets, uses inheritance to
align local workflows. A common problem in these approaches is the mixture between
the different components of the interorganizational workflow, which makes the model
difficult to understand and analyze. Also, the interoperability between the constituent
workflows either is not represented explicitly in the model, or it lacks clarity. These
approaches do not take into consideration the resources involved in the execution of the
local workflows.
This paper presents a new approach on the modelling of interorganizational work-
flows, based on nested Petri nets. Nested Petri nets ([10]) are Petri nets in which tokens
may be Petri nets (object-nets). The paper deals with loosely coupled interorganiza-
tional workflows:there aren local workflow processes which can behaveindependently,
but need to interact at certain points in order to accomplish a global business goal. The
interaction is made through asynchronous or synchronous communication. Resource
constrained interorganizational workflow nets (RIWF-nets) are introduced as a special
case of nested Petri nets, in which the process and the resource perspective of the local
workflows, as well as the communication mechanisms between all the local workflows
are modelled as distinct object-nets. Our model permits the sharing of certain resources
from one organization with other participating workflows. This approach offers a clear
distinction between all the local workflows and the communication structure, ensuring
a modular view over the interorganizational workflow. The paper introduces a notion of
behavioural correctness for RIWF-nets, soundness, and proves this property is decid-
able.
In what follows we will give the basic terminology and notation concerning work-
flow nets. We assume the reader is familiar with the Petri net terminology and notation.
In [1] workflow nets (WF-nets) are introduced for modelling the process perspective: a
WF-net specifies the procedure that handles a single case (workflow instance) at a time.
A WF-net is a Petri net with two special places: a source place, i, and a sink place,
o. In a WF-net there should not be conditions and tasks that do not contribute to the
processing of the case. The two conditions are expressed formally as follows:
A Petri net PN=(P,T,F) is a WF-net iff: (1) PN has a source place i and a sink place
o such that •i = ∅ and o• = ∅. (2) If we add a new transition t
∗
to PN such that
•t
∗
= {o} and t
∗
• = {i}, then the resulted Petri net is strongly connected.
A marking of a WF-net is a multiset m : P → IN (where IN denotes the set of
natural numbers). We write m = 1
′
p
1
+2
′
p
2
for a marking m with m(p
1
) = 1, m(p
2
) =
2 and m(p) = 0, ∀p ∈ P − {p
1
, p
2
}. The marking 1
′
i represents the initial marking of
the net and it is denoted by i. The marking 1
′
o, represents the end of the procedure that
handles the case ( and the final marking of the net, denoted by o ).
The rest of the paper is organized as follows: Section 2 presents an introductory
example of a RIWF-net, Section 3 introduces RIWF-nets, Section 4 defines and studies
the soundness property for RIWF-nets and Section 5 presents the concluding remarks.
30

2 An Introductory Example
In what follows we will present an introductory example of an interorganizationalwork-
flow, modelled by a resource constrained interorganizational workflow net (a RIWF-
net). Our interorganizational workflow consists of two loosely coupled workflows. In
the resource perspective of the first workflow, there are two types of resources, clerks
and economists, which will execute some of the tasks of the workflow. In order to en-
sure the flexibility of the system, resources will be assigned different roles, according to
their capabilities (a resource can play different roles at different moments of time). The
possible roles the resources can take are secretary and manager. The tasks of the work-
flow will be executed by appropriate roles (and not directly by resources). This way
of using resources is called role-based allocation. The specification for the resource
perspective consists in the set of resource types (RT ), the set of roles (RO) and a func-
tion, res, which describes, for each role, the set of resource types that can be mapped
onto that role. In our example, a secretary role can be performed by a clerk, while a
manager role can be performed by an economist. Resources can be allocated dynam-
ically to certain roles. The specification for the resource perspective in our example
is < RT, RO, res >, where RT = {clerks,economists}, RO = {secretary, manager},
res(secretary)={clerks}, res(manager)={economists}. The resource perspective is de-
scribed by the object-net RN
1
(a Petri net, called resource net) in Fig.1. Every element
from RT and RO is described by a place in RN
1
. The transitions assign
secretary and
assign manager allow the system to assign resources to certain roles, according to the
function res. The dual transitions, release secretary and release manager are used to
release the resources from roles. In the process perspective, (described by the extended
WF-net W F
′
1
in Fig.1), task t
1
needs a role secretary for its execution, while t
3
needs
a role manager for its execution . t
′
1
is a special transition which empties the place o
1
.
The specification for the resource perspective of the second workflow is < RT, RO,
res >: RT = {work-rs}, RO = {administrator, supervisor}, res(administrator)=
{workers}, res(supervisor)={workers}. In the process perspective, task t
4
needs an
administrator role for its execution, while task t
5
needs a supervisor role.
In the interorganizational workflow, the workflow processes need to interact at cer-
tain points, according to a certain communication structure. There are two ways of in-
teraction: asynchronous communication and synchronous communication. In our case,
in order to describe the asynchronous communication, we define a partial order on
tasks: AC = {(t
1
, t
4
)} (i.e. task t
1
in W F
′
1
must fire before t
4
in W F
′
2
). Task t
3
in W F
′
1
and task t
6
in W F
′
2
must fire synchronously (there is a synchronous com-
munication between the two workflows, through these transitions). We define the set
of synchronous communication elements: SC = {{t
3
, t
6
}}. The RIWF-net used for
modelling this interorganizational workflow is a nested Petri net which consists of a
system net, SN and of five object- nets. SN is a Petri net with expressions on arcs,
whose places can contain atomic tokens or net-tokens (object-nets). Thus, in the ini-
tial marking of the net, there is an atomic token in place I and all the object-nets re-
side in place p: (W F
′
1
, i
1
), (RN
1
, r
1
0
), r
1
0
= 1
′
clerks + 1
′
economists, (W F
′
2
, i
2
),
(RN
2
, r
2
0
), r
2
0
= 2
′
workers, (C, 0). Some of the transitions of the RIWF-net are
labelled using a partial function, Λ. The transitions from AC will be assigned asyn-
chronous communication labels: Λ(t
1
) = l
1
, Λ(t
4
) = l
2
. The transitions from SC will
31

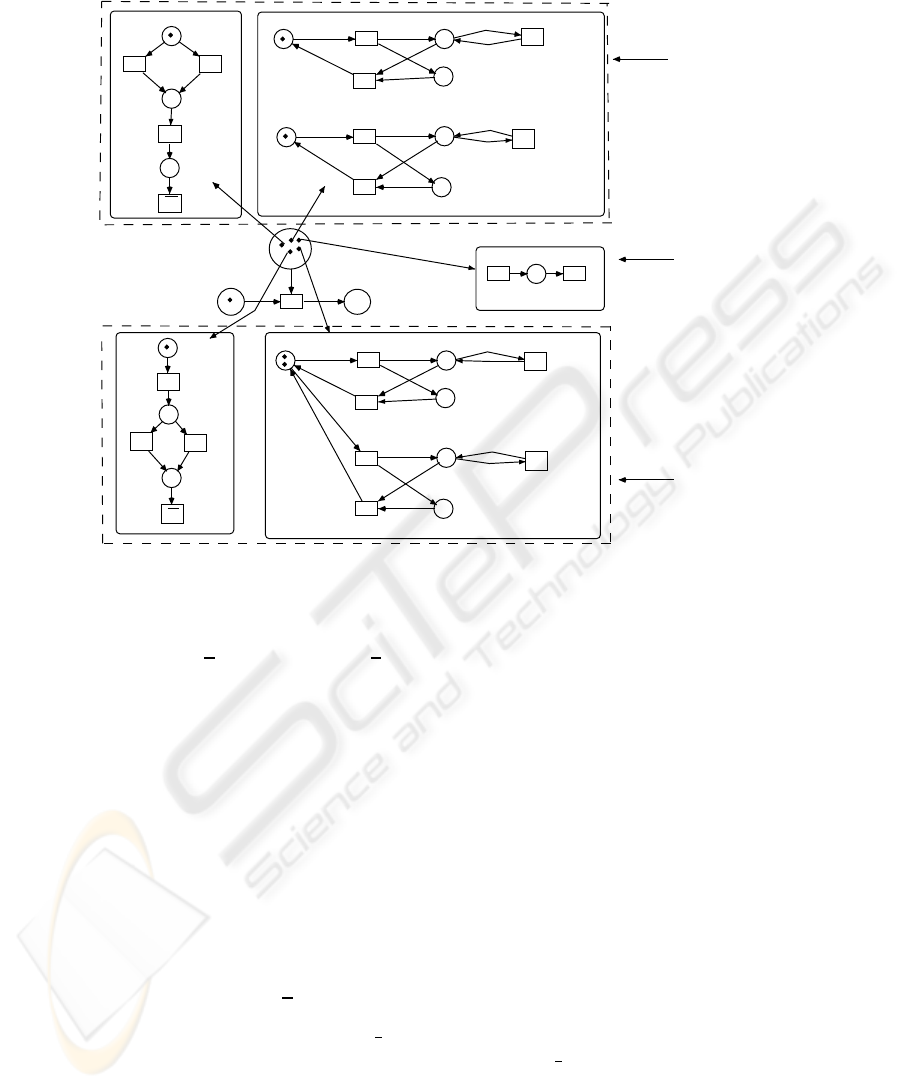
l1
l3
t1
t2
t3
t1’
p1
e
e
e
SN
o1
i1
l2
l3
o2
p2
t4
t5
t6
i2
l2l1
t1_c
p_ac1
release_secretary
R2
release_co
l1
manager
economists assign_co
R1
assign_secretary secretary
clerks
use_admin
R1
R2
supervisor
use_sup
l2
l4
assign_admin
release_admin
assign_sup
release_sup
workers
end
OI
p
(x1,x2,x3,x4,x5)
administrator
the first
local workflow
the second
local workflow
use_secretary
communication
object
use_manager
t4_c
l4
t2’
WF1’
WF2’ RN2
C
l3
RN1
Fig.1. A resource constrained interorganizational workflow net in its initial marking.
be assigned the same synchronous communication label: Λ(t
3
) = Λ(t
6
) = l
3
. We also
have Λ(t
′
1
) = e in W F
′
1
, Λ(t
′
2
) = e in W F
′
2
and Λ(end) = e in SN. The object-net
C describes the asynchronous communication between the local workflows. C is ob-
tained from AC as follows: the set of places is P
C
= {p
ac
1
}, where ac
1
= (t
1
, t
4
). The
transitions (T
C
) correspondto the transitions involved in asynchronouscommunication:
T
C
= {t
1
c
, t
4
c
}. Since ac
1
= (t
1
, t
4
) ∈ AC then we will add the arcs (t
1
c
, p
ac
1
) and
(p
ac
1
, t
4
c
). We have: Λ(t
1
c
) = Λ(t
1
) = l
1
and Λ(t
4
c
) = Λ(t
4
) = l
2
.
In nested Petri nets, there are several firing rules ([10]): an unlabelled transition
from an object-net can fire if the transition is enabled in the object-net (this is an object-
autonomous step). Also, if several labelled transitions, with the same label, from some
object-nets are enabled in those object-nets, then they should fire synchronously. The
simultaneous firing of these transitions is called an horizontal synchronization step. A
labelled transition enabled in SN should fire simultaneously with the transitions from
the object-nets which have a complementary label (this is a vertical synchronization
step). In our example, the transition end from SN should fire simultaneously with the
transitions labelled with
e in the object-nets.
In our example, t
1
in W F
′
1
, use
secretary in RN
1
and t
1
c
in C should fire at the
same time, because they have the same label, l
1
. But use
secretary is not enabled in
RN
1
(i.e. there does not exist a secretary role available yet), so, although t
1
is enabled
32

in W F
′
1
, it cannot fire yet. Transition t
4
is enabled in (W F
′
2
, i
2
). t
4
can only fire at
the same time with t
4
c
in C, but t
4
c
is not enabled in C, because t
1
c
(and t
1
) has not
fired yet. This behaviour is consistent with the restrictions specified in AC: t
4
will fire
after the firing of t
1
. The unlabelled transition assign
secretary is enabled in RN
1
. The
firing of this transition represents an object-autonomous step in RIW F and produces a
token in place secretary. In the resulting marking, the horizontal synchronization step
(; t
1
, use secretary, t
1
c
) can fire and it produces a new marking M
1
such that place I
contains an atomic token and place p contains the object-nets with their corresponding
new markings: (W F
′
1
, m1
1
) (with m1
1
= 1
′
p
1
), (W F
′
2
, i
2
), (C, mc
1
) (with mc
1
=
1
′
p
ac
1
), (RN
1
, r
1
1
) (r
1
1
= 1
′
economists + 1
′
secretary + 1
′
R
1
), (RN
2
, r
2
0
). One
can notice that t
3
in W F
′
1
, t
6
in W F
′
2
and use
manager in RN
1
have the same label,
so they can only fire at the same time. Thus, t
3
and t
6
fire synchronously, as specified
by SC and t
3
fires only if there is a manager role available for its execution. t
6
does
not need a role for its execution (there does not exist a transition labelled with l
3
in
RN
2
). The vertical synchronization step (end; t
′
1
, t
′
2
) can only fire if t
′
1
is enabled in
W F
′
1
and t
′
2
is enabled in W F
′
2
. The firing of this step removes the atomic token from
I, the object-nets from p and adds an atomic token to place O.
3 Definition of Resource Constrained Interorganizational
Workflow Nets
In this section we first present a Petri net model for the resource perspective of a work-
flow, following the approach we used in [13]. A task that needs to be executed for a
specific case is called a work item. Each work item should be performed by a resource
suited for its execution. In order to facilitate the better allocation of resources to work
items, resources are grouped into roles. Thus, instead of assigning work items directly
to resources, work items will be assigned to certain roles. This pattern of represent-
ing and using resources is called ”role-based allocation” ([9,11, 14]). A role is a group
of resources with similar characteristics. We consider that each resource has a general
type. A resource can have more roles (at different moments in time) and each role can
be performed by several resources of different types ([9]).
In our model, for each role one must specify the set of resource types that can
be mapped onto that role. Based on these rules (which are specified at design time),
the system will be able to allocate dynamically resources to the appropriate roles.
Thus, a specification for the resource perspective consists in the following elements:
a set of resource basic types: RT = {T ype
1
, . . . , T yp e
n
}. For each type T ype
i
, i ∈
{1, 2, . . . , n} there is a number n
i
of resources of that type; a set of roles, RO =
{Role
1
, Role
2
, . . . , Role
m
}; for each role r ∈ RO, res(r) represents the resource
types which can be assigned to the role (res(r) ⊆ RT ).
A resource net RN = (P
RN
, T
RN
, F
RN
) can be defined as follows:
- P
RN
= P
RT
∪P
ROLE
∪P
′
where P
RT
= RT , P
ROLE
= RO and P
′
= {R
ki
|Role
i
∈
RO, T ype
k
∈ res(Rol e
i
)}.
- T
RN
= {assign
ki
, r elease
ik
|Role
i
∈ RO, T yp e
k
∈ res(Rol e
i
)}.
- F
RN
= {(T ype
k
, assign
ki
), (assign
ki
, Role
i
), (assign
ki
, R
ki
), (R
ki
, r elease
ik
),
(Role
i
, r elease
ik
), (rele ase
ik
, T ype
k
)|Role
i
∈ RO, T yp e
k
∈ res(Role
i
)}.
33

In the resource net, P
RT
corresponds to the set of resource types and P
ROLE
corre-
sponds to the set of roles. For each role Role
i
and for each resource type T ype
k
∈
res(Role
i
) the following elements are added to the net : a place R
ki
, a transition
assign
ki
which moves a resource from T ype
k
to role Role
i
; a transition release
ik
which releases the resources of type T ype
k
, assigned to Role
i
, when they are not
needed any longer.
In what follows we will define a model, based on nested Petri nets, for loosely cou-
pled interorganizational workflows. We will assume there are n local workflows which
behave independently, but need to interact at certain points, according to a communi-
cation structure. There are two types of communication: asynchronous communication
(corresponding to the exchange of messages) and synchronous communication.
We define, first, extended workflow nets, an extension of the WF-nets, which will be
used for modelling the local workflows from the interorganizational workflow.
Definition 1. Let W F = (P, T, F ) be a WF-net. The extended WF-net is W F
′
=
(P, T
′
, F
′
), where T
′
= T ∪ {t
′
} and F
′
= F ∪ {(o, t
′
)}.
Resource constrained interorganizational workflow nets (RIWF-nets) are defined as
a special class of nested Petri nets.
Definition 2. A resourceconstrained interorganizational workflow net RIWF is a nested
Petri net: RIW F = (V ar, Lab, AC, SC, (C, 0), W F, RN, SN, Λ, Role) such that:
1. V ar is a set of variables.
2. Lab = Lab
AC
∪ Lab
SC
∪ Lab
Res
∪ {e,
e} is a set of labels.
3. W F = {(W F
′
1
, i
1
), . . . , (W F
′
n
, i
n
) } is a set of extended WF-nets.
4. RN = {(RN
1
, r
1
0
), . . . (RN
m
, r
m
0
)} is the set of resource nets.
5. AC is the asynchronous communication relation: AC ⊆ T
◦
× T
◦
, where T
◦
=
∪
k∈{1,...,n}
T
k
, T
k
is the set of transitions from W F
′
k
. If (t, t
′
) ∈ AC, t ∈ T
i
, t
′
∈
T
j
, then i 6= j.
6. SC is the set of synchronous communication elements: SC ⊆ P (T
◦
) and: ∀x, y ∈
SC : x ∩ y = ∅. If t ∈ T
i
, t
′
∈ T
j
, t, t
′
∈ x, x ∈ SC, then i 6= j.
7. C = (P
C
, T
C
, F
C
) is the communication object:
– P
C
= {p
ac
|ac ∈ AC}.
– T
C
= {t
c
|∃(t
′
, t) ∈ AC ∨ (t, t
′
) ∈ AC}.
– F
C
= {(p, t) ∈ P
C
× T
◦
|p = (t
′
, t) ∈ AC} ∪ {(t, p) ∈ T
◦
× P
C
|p = (t, t
′
) ∈
AC}
8. SN = (N, W, M
0
) is the system net of RIWF, such that:
- N = (P
N
, T
N
, F
N
) is a high level Petri net: P
N
= {I, p, O}, T
N
= {end},
F
N
= {(I, end), (p, end), (end, O)}.
- W is the arc labelling function:W (I, end) = 1, W (p, end) = (x
1
, x
2
, . . . , x
n+m+1
),
W (end, O) = 1.
- M
0
is the initial marking of the net: M
0
(I) = 1,
M
0
(p) = ((W F
′
1
, i
1
), . . . , (W F
′
n
, i
n
), (RN
1
, r
1
0
), . . . (RN
m
, r
m
0
), (C, 0)) and
M
0
(O) = 0.
9. Λ is a partial labelling function such that:
– ∀x ∈ SC, ∀t, t
′
∈ x, Λ(t) = Λ(t
′
) = l, l ∈ Lab
SC
.
34

– if t ∈ T
◦
such that (t, t
′
) ∈ AC or (t
′
, t) ∈ AC, then there exists t
c
∈ T
C
:
Λ(t
c
) = Λ(t) = l, l ∈ Lab
AC
.
– Λ(t
′
i
) = e, ∀i ∈ {1, . . . n} and Λ(end) = e.
– ∀t, t
′
∈ T
i
(i ∈ {1, . . . , n}) : Λ(t) 6= Λ(t
′
).
10. Role is a partial function which assigns to a labelled transition t (Λ(t) ∈ Lab
Res
)
from W F
′
i
∈ W F (t 6= t
′
) a role from a resource net RN
j
∈ RN such that:
if Λ(t) = l and R ole (t) = Role
k
then there exists a transition t
∗
in RN
j
with
Λ(t
∗
) = l and (t
∗
, Role
k
), (Role
k
, t
∗
) ∈ F
RN
j
.
In a RIWF-net there are n extended WF-nets modelling the local workflows, m resource
nets and a communication object, C. The set of all the object-nets is denoted by Obj.
V ar is the set of variables in the net, which will take as value an object-net in a certain
marking. La b is a set of labels: the labels in Lab
AC
are used for asynchronous com-
munication elements, the labels from Lab
SC
are used for synchronous communication
elements and the labels from Lab
Res
are used for labelling tasks in resource nets. The
three sets are not necessary disjoint. AC represents the asynchronous communication
relation: if (t, t
′
) ∈ AC, then t must execute before t
′
. SC is the set of synchronous
communication elements: if x ∈ SC, then, all the transitions from x have to execute at
the same time. C is an object-net which describes the asynchronous communication be-
tween the local workflows: if ac = (t, t
′
) ∈ AC, then there is a corresponding place p
ac
in P
C
, two transitions t
c
, t
′
c
∈ T
C
and two arcs (t
c
, p
ac
), (p
ac
, t
′
c
) ∈ F
C
. SN is a Petri
net in which the tokens are either atomic tokens (without inner structure) or net-tokens.
W is a function that assigns to each arc in SN an expression (a tuple of variables or the
constant 1). Λ is a partial function which labels transitions from RIW F . If x ∈ SC,
then all the transitions from x have the same label l ∈ Lab
SC
. For every transition t
involved in an asynchronous communication element, there is a transition t
c
in C such
that: Λ(t) = Λ(t
c
) = l, l ∈ Lab
AC
. Role is a partial function which specifies the roles
needed for executing certain tasks. Some tasks do not need roles for their execution. In
our model, a task from a workflow can be executed by a role belonging to a different
workflow. Also, as the number of resource nets may differ from the number of workflow
nets, different workflows can share the same resource perspective.
We denote by A
net
the net tokens of the RIWF-net: A
net
= {(EN, m) / m is
a marking of EN , EN ∈ Obj}. Then, a marking of a RIWF-net is a function such
that: M (I) ∈ IN, M (O) ∈ IN and M (p) ∈ A
n+m+1
net
. We write M as a vector M =
(M(I), M (p), M (O)).
A binding (of transition end) is a function b : V ar → A
net
. If expr is an expression,
expr(b) denotes the evaluation of expr in binding b.
Transition end from the system net SN of a RIWF-net is enabled in a marking M
w.r.t. a binding b if and only if: ∀q ∈ •end : W (q, end)(b) = M(q).
There are several types of steps, defining the behaviour of nested Petri nets (see
[10]). In the case of RIWF-nets, we only focus on vertical synchronization, object-
autonomous steps and horizontal synchronization.
There is only one vertical synchronization step in our case: if transition end is en-
abled in a marking M w.r.t. a binding b and every transition t
′
i
(Λ(t
′
i
) =
e) is enabled
in the object-net b(x
i
) = (W F
′
i
, m
i
), ∀i ∈ {1, . . . , n}, then the simultaneous firing of
35

end and t
′
1
, . . . , t
′
n
is a vertical synchronization step. The firing of the vertical synchro-
nization step (end; t
′
1
, . . . , t
′
n
) in marking M produces the marking M
′
= (0, 0, 1).
An object - autonomous step, in our case, represents the firing of an unlabelled
transition in an object-net from the place p.
A horizontal synchronization step represents the simultaneous firing of the tran-
sitions with the same labels from object-nets: Let M be a marking of RIW F and
α = (α
1
, α
2
, . . . , α
m+n+1
) the tuple of net-tokens from p. Assume t
1
, . . . t
s
is the set
of all the transitions with the same label l 6=
e, Λ(t
1
) = Λ(t
2
) = . . . = Λ(t
s
) =
l, such that: every transition t
j
(j ∈ {1, . . . , s}) is enabled in a net-token α
k
j
=
(EN
j
, m
j
) ({k
1
, . . . k
s
} ⊆ {1, . . . , m + n + 1}, EN
j
∈ Obj ) and m
j
[t
j
im
′
j
(by
means of classical Petri nets). The synchronous firing of t
1
, . . . , t
s
is called a hori-
zontal synchronization step. The resulting marking, M
′
, is obtained from M by re-
placing the tuple α from place p with the tuple (α
′
1
, α
′
2
, . . . , α
′
m+n+1
), where α
′
k
j
=
(EN
j
, m
′
j
), ∀j ∈ {1, . . . , s} and α
′
i
= α
i
, ∀i ∈ {1, . . . , m + n + 1} \ {k
1
, . . . k
s
}. We
write: M[; t
1
, . . . , t
s
iM
′
.
4 The Soundness Property for Resource Constrained
Interorganizational Workflow Nets
In this section we will introduce a notion of soundness for RIWF-nets.
A notion of soundness was defined for WF-nets, expressing the minimal conditions
a correct workflow should satisfy ([1]): a workflow must always be able to complete a
case ((∀m)((i[∗im) =⇒ (m[∗ io))), any case must terminate correctly (∀m)((i[∗im)∧
m ≥ o) =⇒ (m = o)), and every task should contribute to at least one possible
execution of the workflow (∀t ∈ T )(∃m, m
′
)(i[∗im[tim
′
).
It was proven (see [1]) that the soundness property is decidable for WF-nets.
An extended workflow net W F
′
is sound if its underlying net,W F , is sound.
In an interorganizational workflow, although the local workflows are sound, we can
have synchronization errors and interlockings. We will define a notion of soundness
for interorganizational workflows. The final state for a RIWF-net is a marking M
f
, in
which there is only one atomic token in place O: M
f
= (0, 0, 1). A RIWF-net is sound
if: (1) every extended WF-net W F
′
i
(i ∈ {1, . . . , n}) is sound and (2) for any reachable
marking of the IWF-net, there is a firing sequence that leads to M
f
. We can define
formally the notion of soundness for a RIWF-net as follows:
Definition 3. A RIWF-net is sound if and only if:
1. (W F
′
j
, i
j
) is a sound extended workflow net, ∀j ∈ {1, . . . , n}.
2. (∀M)((M
0
[∗iM) =⇒ (M [∗iM
f
)).
The second condition from the definition basically states that the interorganizational
workflow is sound if the termination condition still holds for every WF-net, when the
firing of tasks is restricted by the communication structure and the resources involved.
In order to decide whether the soundness property defined is decidable, we introduce
a partial order on the markings of the RIWF - net (see [10]):
36

Definition 4. Let RIW F be a RIWF-net, M
1
and M
2
markings of RIW F . M
1
 M
2
if and only if M
1
(I) ≤ M
2
(I), M
1
(O) ≤ M
2
(O) and there is an embedding J
p
:
M
1
(p) → M
2
(p), such that for α = (α
1
, . . . , α
n+m+1
) ∈ M
1
(p) and for J
p
(α) =
α
′
= (α
′
1
, . . . α
′
n+m+1
) we have for i ∈ {1, . . . , n + m + 1} either α
i
= α
′
i
or
α
i
= (EN, m) and α
′
i
= (EN, m
′
) (EN ∈ Obj) and for all the places q of EN:
m(q) ≤ m
′
(q).
Let RIW F be a RIWF-net and M and M
′
two markings of RIW F . The marking
M covers M
′
(w.r.t. the partial ordering ) if M
′
 M.
Given a set of markings Q = {q
1
, q
2
, . . . , q
n
} and an initial marking M , the in-
evitability problem is to decide whether all computations starting from M eventually
visit a marking not covering (w.r.t. the partial ordering ) one of the markings from Q.
It was proven in [10] that the inevitability problem is decidable for nested Petri nets.
Theorem 1. Let RIW F be a RIWF-net and M ∈ [M
0
i. There is a firing sequence
M[∗iM
f
if and only if there is a firing sequence M [∗iM
′
and M
′
does not cover (w.r.t.
) the marking (1, 0, 0).
Proof: (=⇒) Assume M[∗iM
f
in RIW F . Since M
f
does not cover the marking
(1, 0, 0), we can consider M
′
= M
f
.
(⇐=) We assume there exists a firing sequence from marking M to a marking M
′
which does not coverthe marking (1, 0, 0). If M
′
does not cover (1, 0, 0), then M
′
(I) =
0. M
′
is reachable from M
0
(because M
0
[∗iM [∗iM
′
). M
′
(I) = 0 if and only if the
vertical synchronization step Y = (end[b]; t
′
1
, . . . , t
′
n
) fires in RIW F . The firing of
this step always leads to the marking M
f
(so, M
′
= M
f
). This implies there is a firing
sequence such that M[∗iM
f
.
Theorem 2. The soundness problem is decidable for RIWF - nets.
Proof: Let RIW F be a RIWF-net. RIW F is sound if and only if: (1) W F
′
i
are sound,
∀i ∈ {1, . . . , n} and (2) for any reachable marking in RIW F , M ∈ [M
0
i, there exists
a firing sequence M[∗iM
′
such that M
′
does not cover (w.r.t. ) the marking (1, 0, 0).
The soundness of the extended WF-nets is decidable (because the soundness for WF-net
is decidable) and condition (2) is equivalent to the inevitability problem, if we consider
the marking M and the set of markings Q = {(1, 0, 0)}.
5 Conclusions
The approach we propose in this paper has several advantages: one can have a modu-
lar view on the interorganizational workflow; steps in RIWF- nets can easily express
the synchronous and the asynchronous communication; RIWF-nets represent a flexi-
ble model for interorganizational workflows, because any component can be modified
easily, with minimal changes to the other components. A notion of soundness was in-
troduced for RIWF-nets and we proved this property is decidable. Future work aims
at defining a specification language based on XML, which will then be translated into
RIWF-nets, in order to check the soundness and other behavioural properties of the in-
terorganizational workflow. We intend to develop a tool based on this language and on
RIWF-nets, for executing interorganizational workflows. We will also study the case in
which every local workflow processes batches of cases, instead of one case in isolation.
37

References
1. W. M. P. van der Aalst: Verification of Workflow Nets. P. Azema and G. Balbo, editors, Ap-
plication and Theory of Petri nets 1997, volume 1248 of Lecture Notes in Computer Science,
pp. 407-426, SpringerVerlag, Berlin, 1997.
2. W.M.P. van der Aalst: Three Good Reasons for Using a Petri-net-based Workflow Manage-
ment System. Wakayama et al., editors. Information and Process Integration in Enterprises:
Rethinking Documents. Volume 428 of The Kluwer International Series in Engineering and
Computer Science. Boston, Kluwer Academic Publicers, pp.161-182, 1998.
3. W.M.P. van der Aalst. Loosely coupled interorganizational workflows: Modeling and ana-
lyzing workflows crossing organizational boundaries. Information and Management, vol.37,
no.2, pp.6775, 2000.
4. W.M.P. van der Aalst and M. Weske. The P2P approach to Interorganizational Workflows.
In K.R. Dittrich, A. Geppert, and M.C. Norrie, editors, Proceedings of the 13th International
Conference on Advanced Information Systems Engineering (CAiSE’01), volume 2068 of
Lecture Notes in Computer Science, pages 140156. Springer-Verlag, Berlin, 2001.
5. R.W.H. Bons, R.M. Lee, and R.W. Wagenaar. Designing trustworthy interorganizational
trade procedures for open electronic commerce. International Journal of Electronic Com-
merce, 2(3): pp. 6183, 1998.
6. T.L. Casavant, J.G. Kuhl. A Communicating Finite Automata Approach to Modeling Dis-
tributed Computation and its Application to Distributed Decision-Making. IEEE trans. on
computers, May 1990,Vol. 39, No. 5, pp. 628-639.
7. Jiang Guo. Using Category Theory to Model Software Component Dependencies. Proc. of
9th Annual IEEE Intl. Conf. and Workshop on the Engineering of Computer-Based Sys-
tems(ECBS 2002) ,Lund, Sweden, IEEE Computer Society Press, April 08 - 11, 2002, pp.
185-194.
8. G. Kramler , W. Retschitzegger. Specification of Interorganizational Workflows - A Com-
parison of Approaches. Vienna, Austria: Institute of Software Technology and Interactive
Systems, Business Informatics Group, Vienna University of Technology, 2002. Technical
Report, 08/02.
9. A. Kumar, W.M.P. van der Aalst, H.M.W. Verbeek: Dynamic Work Distribution in Workflow
Management Systems: How to balance quality and performance?. Journal of Management
Information Systems, 18(3), pp.157-193, 2002.
10. I.A. Lomazova: Nested Petri Nets - a Formalism for Specification and Verification of Multi -
Agent Distributed Systems. Fundamenta Informaticae 43 pp. 195-214, 2000.
11. M. zur M¨uhlen. Resource modeling in workflow applications. Proceedings of the 1999 Work-
flow Management Conference (November 1999), pp. 137-153, 1999.
12. M. Netjes, W.M.P. van der Aalst, H.A. Reijers. Analysis of resource-constrained processes
with colored petri nets. In K. Jensen, Proceedings of the 6th Workshop and Tutorial on Prac-
tical Use of Coloured Petri nets and the CPN Tools (CPN’05), pp. 251-265, 2005
13. O. Prisecaru: Resource Workflow Nets:a Petri Net Formalism for Workflow Modelling. In
Proc. of MSVVEIS 2007, pp. 11-21, Portugal, 12-13 June 2007
14. I.T.P. Vanderfeesten, W.M.P. van der Aalst, H.A. Reijers. Modelling a product based work-
flow system in CPN Tools. In K. Jensen, Proceedings of the 6th Workshop and Tutorial on
Practical Use of Coloured Petri Nets and the CPN Tools, pp. 99-118, Aarhus, Denmark:
University of Denmark, 2005.
15. H. M. W. Verbeek, A. Hirnschall, Wil M. P. van der Aalst. XRL/Flower: Supporting Inter-
organizational Workflows Using XML/Petri-Net Technology. Proceedings of Web Services,
E-Business, and the Semantic Web, WES 2002, Toronto, Canada, May 2002,pp. 93-108.
38