
An Executable Semantics of Object-oriented Models for
Simulation and Theorem Proving
Kenro Yatake and Takuya Katayama
Japan Advanced Institute of Science and Technology
1-1 Asahidai Nomi Ishikawa 923-1292, Japan
Abstract. This paper presents an executable semantics of OO models. We made
it possible to conduct both simulation and theorem proving on the semantics by
implementing its underlying heap memory structure within the expressive inter-
section of the functional language ML and the theorem prover HOL. This paper
also presents a verification system ObjectLogic which supports simulation and
theorem proving of OO models based on the executable semantics. As an appli-
cation example, we show a verification of a UML model of a practical firewall
system.
1 Introduction
As our society has become more dependent on the information systems, it has become
more important to ensure the correctness and validity of those systems. Especially, there
is a growing need for the verification on the analysis level of the development since the
scale of systems is becoming large and the bugs found in the coding stage lead to a fatal
loss for constructors. Verification on the analysis levels allows early detection of bugs
and, as a result, reduces the total cost of development.
Among many verification methods, we focus on theorem proving which is recently
gathering attention in industrial areas. The prominent feature of theorem proving is
induction by which we can prove the correctness of system behavior exhaustively for
arbitrary inputs. In order to apply theorem proving to the analysis models such as UML
(Unified Modeling Language [1]), we need to implement a formal semantics of OO
models in theorem provers.
We consider that the semantics should be executable. This is because an executable
semantics allows us to conduct not only theorem proving but also simulation. Even
though theorem proving is quite a powerful verification method, it is not efficient when
it comes to thecost-effectivenessbecause it requires manual interventionof users through
proofs. But, simulation can, to some extent, compensate the disadvantage of theorem
proving. Simulation is efficient in that it allows us to identify the result of system execu-
tion at a glance. Although it cannot ensure the 100% correctness, we can immediately
check if the result is apparently correct or not. This is especially useful in the early
stage of model construction where many trivial bugs are included. By simulation, we
can efficiently find trivial bugs in advance of high-cost theorem proving, and as a result,
we can optimize the total cost of verification.
Yatake K. and Katayama T. (2008).
An Executable Semantics of Object-oriented Models for Simulation and Theorem Proving.
In Proceedings of the 6th International Workshop on Modelling, Simulation, Verification and Validation of Enterprise Information Systems, pages 71-80
DOI: 10.5220/0001732500710080
Copyright
c
SciTePress

So far, we have implemented a semantics of OO models as a theory in the theorem
prover HOL [2] and conducted verification of a simple library system [16]. But, only
theorem proving was possible because the semantics was not executable. So this time,
for the purpose of simulation, we made the semantics executable by implementing it
in the functional language Moscow ML [3] (the meta-language of HOL). In HOL, the
semantics is implemented based on a heap memory structure, i.e. The types and opera-
tions in the semantics are represented by those of the heap memory, and all the axioms
are derived from their definition. We implemented the same data structure as actual op-
eration in ML and made the semantics directly executable. The trick is that this memory
structure is implemented within the intersection of the expressive power of HOL and
ML. This makes it possible to implement the semantically equivalent memory struc-
tures both in HOL and ML. To have an equivalent semantics is important to make the
result of simulation and theorem proving consistent with each other.
In this paper, we present the overview of the executable semantics and its implemen-
tation. We also present a verification system ObjectLogic which supports simulation
and theorem proving of OO models based on the executable semantics. As an applica-
tion, we show a verification of a firewall system where we proved that UML sequence
diagrams satisfies constraints written in OCL (Object Constraint Language [4]).
This paper is organized as follows. Section 2 explains the overviewof the executable
semantics. Section 3 explains its implementation. Section 4 explains how to execute the
semantics. Section 5 introduces ObjectLogic. Section 6 shows a verification of a firewall
system. Section 7 cites related works. Section 8 gives conclusion and future work.
2 The OO Semantics
We implemented the OO semantics as a theory in HOL. The theory is not specific
to particular models, but implements general OO concepts so that it can be used as
a groundwork for various models. The OO concepts covered are classes, attributes,
inheritance (tree), object subtyping and method dynamic dispatching. Besides covering
general OO concepts, it has two characteristics. Firstly, it allows arbitrary types (without
type variables) to be embedded into the types of object attributes (fields). Compared to
the verification on the program level, verification on the analysis level requires high-
availability of types since the analysis models are abstracted by various types such as
set, stack and date. In fact, UML, the most major modeling language, does not limit
available types to particular ones. Therefore, we enabled attributes to have arbitrary
types. This feature is also beneficial in that we can utilize various types and pre-proved
theorems in HOL libraries when constructing models and performing proofs. But it is
not so easy to realize this feature in the first-order types of HOL. The problem lies
in the structure of objects, i.e. an object is a data which holds multiple attributes of
arbitrary types. So, we cannot represent objects by naively taking a product of type
variables like α ∗ β ∗ γ ∗ ... because we cannot predict how many variables we should
put in the product. To cope with this problem, we take the approach of automatically
constructing the semantics depending on the type information of the application. If
types are given in advance, an object is easily represented by a product of those types
like num ∗ string ∗ bool. The object referencing and inheritance are realized by putting
72
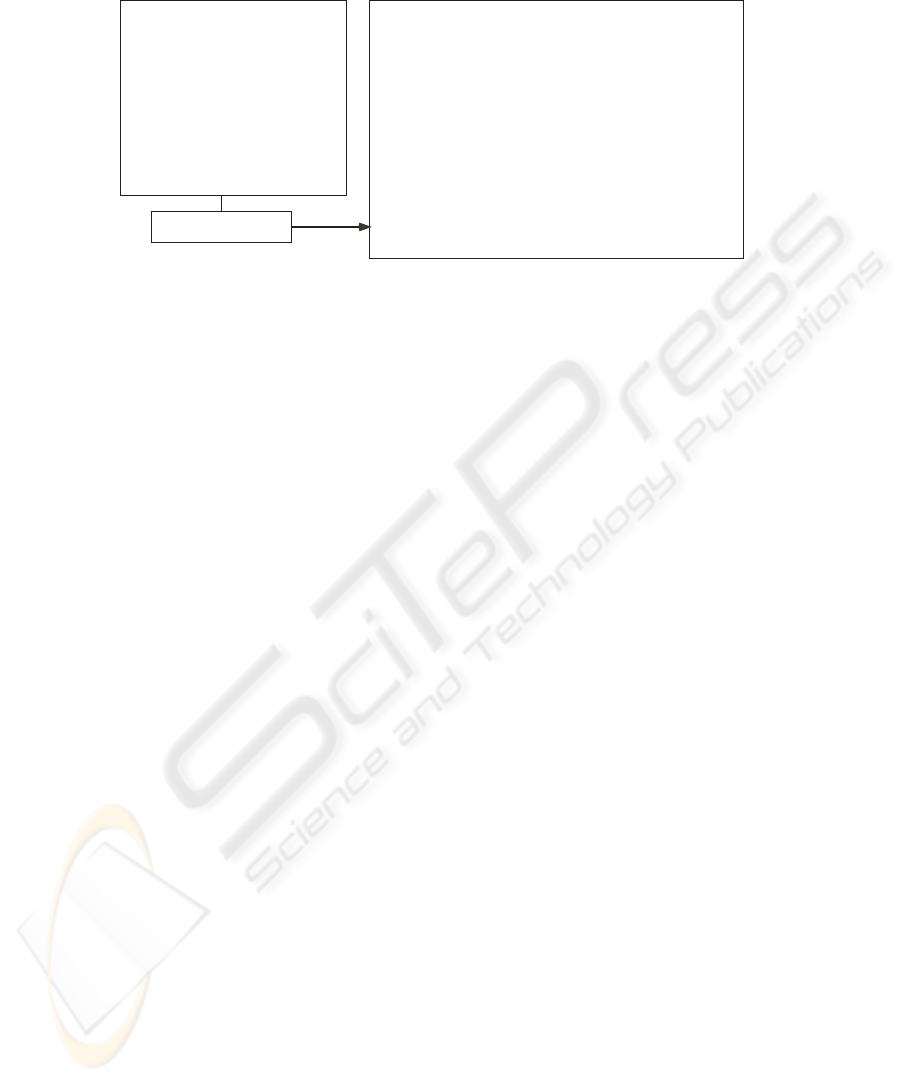
Theory generator
class fig {
attr x : int;
attr y : int;
}
class rect extends fig {
attr w : int;
attr h : int;
}
class crect extends rect {
attr c : color;
}
Class model
[types] store, fig, rect, crect
[constants & operators]
store_emp, fig_null, rect_null, crect_null
fig_new : store -> fig # store
fig_ex : fig -> store -> bool
fig_get_x : fig -> store -> int
fig_set_x : fig -> int -> store -> store
rect_cast_fig : rect -> store -> fig
fig_is_rect : fig -> store -> bool
...
[axioms]
|- !s. let (f,s1) = fig_new s in fig_ex f s1
|- !f x s. fig_ex f s ==>
(fig_get_x f (fig_set_x f x s) = x)
|- !r s. rect_is_rect r s ==>
fig_is_rect (rect_cast_fig r s) s
...
OO theory
Fig.1. The OO theory.
those products in a heap memory structure. The implementation details are explained in
the next section. Secondly, it is shallowly embedded, i.e. the concepts such as classes,
attributes, and inheritance are represented directly as types and constants in HOL. This
is because our verification target is each instance of OO models. Shallow embedding
facilitates the proof of instance levels compared to deep embedding [5]. It also has
the effect of making the theory simple because all the typing information is directly
represented by the type system of HOL and there is no need to additionally include the
typing constraints into the theory.
The OO theory is defined based on the class model of the target system. We im-
plemented the theory generator which inputs a class model and outputs its OO theory.
Fig.1 shows an example. The class model defines static structure of a system such as
classes, attributes and inheritance. The OO theory defines types, operators and axioms
representing basic OO concepts. The type playing central part in the theory is store.
It represents the environment which holds all alive objects in the system and has the
constant store_emp representing an empty store. The type fig represents the type of
object references for the class fig and has the constant fig_null representing NULL
reference. The operator fig_new is a function to create a new fig instance in the store.
The operator fig_ex is a predicate to test if a fig object exists in the store. The first
axiom is a property about these operators saying “The newly created fig object is alive
in the store after the creation.” The operators fig_get_x and fig_set_x are func-
tions to read and write the attribute x of the class fig. The second axiom says “If the
fig object is alive in the store, the value of the attribute x of the object obtained just
after updating it to v equals to v.” The operator fig_cast_rect is a function to cast
a fig object downward from fig to rect. The operator fig_is_rect is a predicate
to test if a fig object is an instance of the class rect. After an object is created, its
apparent type can be changed by cast operators, but instance-of operators remember the
actual type of the object. The third axiom illustrates this. It says “If a rect object is an
instance of the rect class, it is still the instance of the rect class even if it is cast to
the fig class.” The instance-of operators are used to implement the dynamic method
dispatching.
73

(2,3,r0)
f0
f1
f2
f3
f4
(-4,5,r1)
(1,-2,r2)
(10,0,r3)
(10,8,f2,c0)
r0
r1
r2
r3
(6,12,f3,c1)
(4,10,f4,c0)
(red,r2)
c0
c1
fig
rect
crect
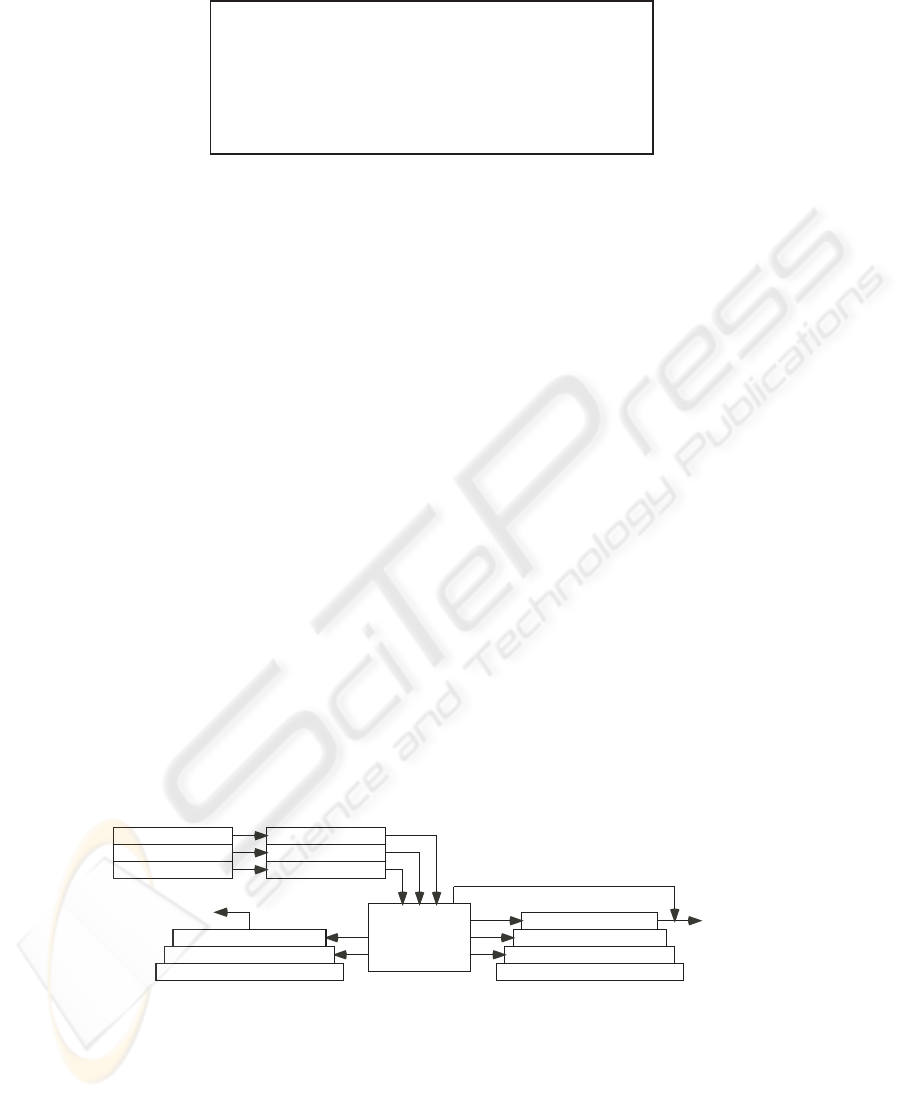
Fig.2. Snapshot of the heap memory.
3 Implementation in HOL
In order to guarantee the soundness of the theory, we implemented the theory conserva-
tively by definitional extension. This is a standard method to construct sound theories
in HOL, where new theories are derived from existing sound theories by only allowing
introduction of definition and derivation by sound inference rules. This can be com-
parable to axiomatical theory construction where axioms are directly introduced in the
theory, which often makes the theory inconsistent. The theory is derived from a heap
memory structure which is defined by primitive theories already existing in HOL. The
types and constants in the theory are represented by those in the heap memory and the
axioms are derived from their definitions.
Fig.2 shows a snapshot of the heap memory for the example model. The heap mem-
ory consists of three sub-heaps which are introduced corresponding to the three classes.
Each sub-heap is represented by a list and the whole heap is represented by a tuple of
them. Object references are represented by indices of the memory. For example, the ref-
erences f0, f1, f2,... are represented by natural numbers 0,1,2, ... (f0 represents a null
reference fig_null). Object instances are represented by a tuple or multiple tuples
stored in the sub-heaps. For example, the tuple in f1 represents a fig instance whose
attribute are x=2 and y=3. Two tuples in f2 and r1 together represent a rect instance
whose attribute are x=-4, y=5, w=10, and h=8. The two tuples are linked by storing
the references r1 and f2 each other. Object subtyping is modeled by this linked-tuple
structure. For example, the three references f3, r2 and c1 all point at the same crect
instance. This means the crect instance can have three apparent types fig, rect and
crect. The operators in the theory are implemented as the functions to manipulate the
heap memory. Their definition is detailed in [16].
4 Executing the Semantics
In HOL, the theory is derived from the heap memory structure. By defining the same
data structure in ML, the theory becomes executable. It is known that HOL and ML
have similar type systems and there exists an intersection of expressiveness between
them. Fig.3 illustrates this. The common concepts are inductive datatypes and recursive
functions (primitive recursion and well-founded recursion) [8][9]D The heap memory
structure in HOL is defined within this intersection and the same data structure can be
defined in ML in a straightforward way.
For example, the following HOL function write is the function on the sub-heap l
to update the data in the address n by data x:
74

inductive datatypes
recursive functions
(prim rec. w.f. rec.)
inductive relations,
undefined constants
quantifiers...
exception,
non-terminating functions,
modules...
HOL ML
Fig.3. Expressiveness of HOL and ML.
write (n:num) (x:’a) (l:’a list) =
if 0 < n /\ n < LENGTH l then write1 n x l else l
(write1 0 x l = x::(TL l)) /\
(write1 (SUC n) x l) = (HD l)::(write1 n x (TL l))
This primitive recursive function can be also defined in ML as follows:
fun write (n:int) (x:’a) (l:’a list) =
if 0 < n andalso n < length l then write1 n x l else l
fun write1 0 x l = x::(tl l)
| write1 n x l = (hd l)::(write1 (n-1) x (tl l))
We can see that the definition is directly correspondent except that we are using the
integer type int in ML instead of the natural number type num. This is because ML
does not have a type of natural numbers. This does not make any difference in their se-
mantics. As for exception, we cannot use ML exception because HOL does not have the
concept. In Java, exceptions are raised in the cases such as NULL reference accessing
and illegal down-casting. We handle such cases by returning appropriate values. This is
summarized by the following axioms:
|- !s. fig_get_x fig_null s = 0
|- !x s. fig_set_x fig_null x s = s
|- !f s. fig_is_fig f s ==> (fig_cast_rect f s = rect_null)
The first axiom means “When an attribute of a NULL reference is referred, it returns
the default value for the attribute type.” The alternative approach could be to return
an undefined constant like fig_unknown_x:int, but as it is not supported in ML,
we simply return the default value. The second axiom means “When an attribute of a
NULL reference is updated, it actually does not cause the effect to the state.” The third
axiom means “When illegal down-casting occurs, it returns the NULL reference of the
destination class.”
In this way, we can define a semantically equivalent heap memory structures both
in HOL and ML. To have an equivalent semantics is important to make the result of
simulation and theorem proving consistent with each other.
We extended the theory generator so that it outputs the ML structure which imple-
ments the heap memory structure. Its signature provides the types and operators corre-
sponding to those in the OO theory. Fig.4 shows the execution of those operators. The
internal structure of objects and stores are hidden by the opaque signature restriction.
75
- val (r,s1) = rect_new store_emp;
> val r = <rect> : rect
> val s1 = <store> : store
- val s2 = rect_set_x r 10 s1;
> val s2 = <store> : store
- val f = rect_cast_fig r s2;
> val f = <fig> : fig
- fig_get_x f s2;
> val it = 10 : int
Fig.4. Execution of the theory.
5 ObjectLogic
ObjectLogic is a verification system for OO models. It supports both simulation and
theorem proving based on our executable semantics. It enables us to define models
in a high-level language called OML (ObjectLogic Meta-Language). It is a sequential
OO language whose syntax is closed to Java and is able to import arbitrary types and
functions from HOL. In OML, we can specify assertions such as method contracts (pre-
and post-conditions) and class invariants. From the assertions, ObjectLogic produces
target propositions (proof obligation) in the OO theory. It also provides tactics which
tries to prove the goal automatically by applying the axioms in the theory.
Fig.5 shows how it works. Firstly, ObjectLogic constructs the simulator and the the-
ory from the classes using the theory generator (1). Then, it translates methods into
functions both on the simulator and the theory (2). Finally, it translates assertions into
HOL propositions (3). We can conduct simulation using the ML executables and theo-
rem proving by proving the HOL propositions.
ObjectLogic can be used for verification of UML models. As shown in Fig.5, all we
have to do is to translate UML class diagrams, sequence diagrams and OCL constraints
into classes, methods and assertions in OML (Currently, this translation is done by hand
and future version of ObjectLogic will support automatic translation). We can provethat
the internal behavior of the sequence diagrams satisfies the method contracts and class
invariants defined as OCL constraints in the class diagram.
OO theory
HOL
Assertions
Classes
Methods
OML
Functions
Propositions
Q.E.D
Tactics
OCL
Class diag.
Seq. diag.
UML
ObjectLogic
Simulator
ML
Functions
(1) (1)
(2)
(1)
(2)
(2)
(3)
(3)
Simulation
Fig.5. ObjectLogic.
76
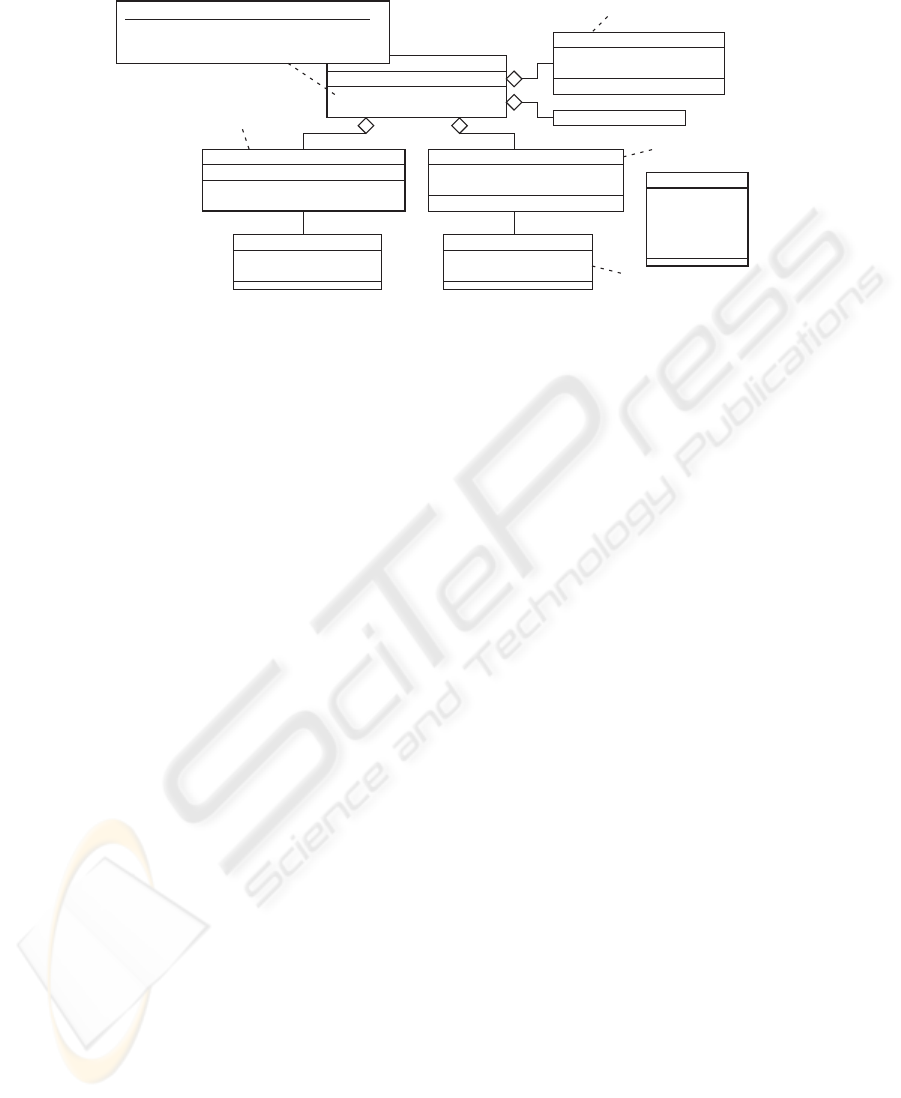
+filterOut
(p:packet):string#packet
fw
-active:bool
-srcIP:num
-dstIP:num
-srcPort:num
-dstPort:num
-protocol:num
packet
+check(p:packet):bool
frule
-srcIPTable:num list
-dstIPTable:num list
doscounter
-localAddr:num#num
-globalAddr:num#num
connection
+addConnection
(la:num#num,ga:num#num):void
-maxSize:num
contable
+srcnat(sa:num#num):num#num
-ipAddr:num
-ports:(num#bool)list
nattable
-localAddr:num#num
-globalAddr:num#num
natrule
0..maxSize 0..length(ports)
fw::filterOut(p:packet):string#packet
pre: not (p=null)
post: not(snd(result)=null) implies
(snd(result)).srcIP=nattable.ipAddr@pre
Connection table
NAT table
NAT rule
Filter rule
Fig.6. UML class diagram of the firewall system.
6 Verification of a Firewall System
We applied ObjectLogic to verification of a practical firewall system. The specification
of the firewall system is our original one based on a real product of a company close
to Cisco
R
PIX Firewall. We conducted verification as follows. Firstly, we translated
the specification into UML models (structural part into class diagrams and behavioral
part into sequence diagrams) and the requirements into constraints in OCL. Then, we
translated the UML models and the OCL constraints into OML and input it to Object-
Logic obtaining the ML executables and the HOL propositions. Finally, we conducted
simulation using the executables and proved propositions in HOL. The OML code is
about 1200 lines containing 8 classes, 35 attributes and 102 methods.
The firewall system is a stateful packet filter with NAT (Network Address Transla-
tion) which is the mechanism to translate between a public IP address of the firewall
and multiple private IP addresses of local hosts. It has dual effects of sharing a single
IP address among multiple hosts and hiding private addresses of the local hosts. Fig.6
shows the class diagram of the firewall system. The model is abstracted with respect to
datatypes using HOL types. For example, IP addresses are represented by natural num-
bers and the filter rules are represented by lists of permissible address numbers. The key
function of the system is the packet filtering function which is defined as the method
filterOut() of the class fw. It inputs a packet and outputs a string message and the
filtered packet. The internal behavior of this method is defined as sequence diagrams,
which we omit to show due to space limitation.
For this firewall, we conducted simulation and theorem proving to verify the prop-
erties such as “The outbound packets which do not meet the filter rules are always
dropped unless they belong to existing connections” and “The source IP address of the
outbound packet is always updated by the public IP address of the firewall”. Both of
them are crucial for the security of the firewall. The first property ensures that a local
host never connects to illegal hosts in the outside network. The second property (NAT
property) ensures that the private IP addresses of the local network never leak to the
77
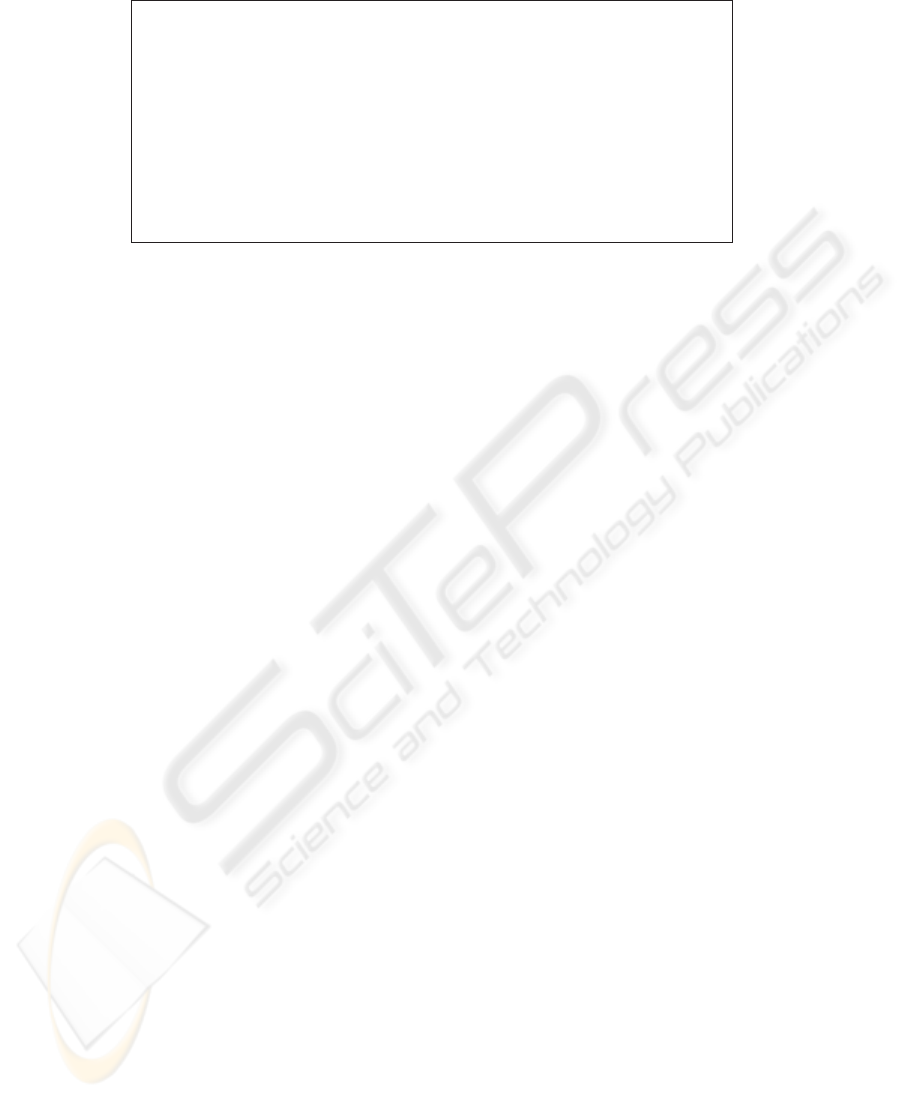
- val (fw,s) = new_fw store_emp; (* Creat a FW *)
(* Set confuguration values *)
- val (_,s) = fw_setIpAddr pfm 200 s;
- val (_,s) = fw_setPorts pfm [1200,1210,1220] s;
- val (_,s) = fw_setFilterRules pfm SRCADDR [10,20,30] s;
...
- val (p,s) = new_packet 20 1070 250 80 TCP s; (* Create a packet *)
> val p = <packet> : packet
val s = <store> : store
- val (msg,p,s) = fw_filterOut fw p s; (* Apply outbound filtering *)
> val msg = "pass: new connection" : string
val p = <packet> : packet
val s = <store> : store
- packet_getInfo p s; (* Display packet information *)
> val it = ((200, 1200), (250, 80), 0) : (int * int) * (int * int) * int
...
Fig.7. Simulation of the firewall system.
outside network. The class diagram includes the OCL constraint representing the NAT
property which is defined as the contract of the method filterOut().
Fig.7 shows simulation of the firewall. We firstly created a firewall object and set
the configuration values such as the public IP address, the port numbers and the filter
rules. Then, we applied the filtering function to an outbound packet and identified that
the firewall correctly passed the packet and updated the source IP address by the NAT
rule. By simulation, we were able to find some trivial bugs. For example, we found the
lack of method invocation to add a connection by seeing the result where the connection
table remained unchanged. We also found that then- and else-parts of if statement
were reversed by seeing the result where an apparently correct packet was dropped. We
were able to find these kinds of easy bugs efficiently by simulation and avoid the worst
case to find them by high-cost theorem proving.
The NAT property is proved in HOL as the following theorem:
|- !(this:fw) (p:packet) (s:store).
let (msg,p’,s’) = fw_filterOut this p s in
packet_ex p s /\ invariants fw s ==>
packet_ex p’ s’ ==>
(packet_getSrcAddr p’ s’ = fw_getIpAddr this s)
The function fw_filterOut represents the filtering method of the firewall. It means
“If the output packet p’ is not NULL (the packet is passed), the source IP address of
p’ is equal to the public IP address of the firewall.” By this theorem, we can ensure that
private addresses never leak outside. The proof took 8 hours and we proved 21 lemmas
in the course. The proof code length is about 450 lines (about one tactic per line). The
entire proof is done in the OO theory level using the tactics in ObjectLogic without
digging down to the heap memory level. To be able to conduct proof in the OO level,
which is close to human intuition, is the major advantage of ObjectLogic.
In this way, ObjectLogic enables both simulation and theorem proving in the equiv-
alent semantics in ML and HOL. By proving crucial properties of the firewall system,
we made sure that ObjectLogic can be applicable to practical systems of proper scale.
In order to make it applicable to general large systems, we need to make the proof
more efficient. The key is how efficient we can make the inference of loop statements.
78

We consider it effective to introduce high-level loop statements for manipulating object
collections and their inference rules because they freqently appear in application do-
mains: calculate the interest for all the accounts in a bank, calculate the total price of
all the items in the cart in online shopping sites. It is also effective to implement a ver-
ification condition generator for OML. To prove verification conditions is much more
efficient than to prove propositions directly in the OO theory because we can focus on
the proof of datatypes apart from the axioms in the OO theory.
7 Related Work
The semantic equivalence between simulation and theorem proving is a notable feature
of our executable semantics, which is realized by defining it in the expressive intersec-
tion of ML and HOL. This is similar to ACL2 which combines a theorem prover and
a programming language based on the same language, an applicative subset of Com-
mon Lisp. ACL2 is often used as a semantics for both simulation and theorem proving.
The work by G. Al Sammane [14] presents a tool TheoSim which combines simulation
and theorem proving of VHDL designs. The work by M. Wilding et al. [15] defines
a formal model of a microprocessor to integrate simulation and formal analysis. Even
though ACL2 is successful in hardware verification, we consider it has a limitation in
software verification because the representation is low level and the types are limited
to numerals. On the other hand, our tool ObjectLogic is suited for software verification
because it supports objects and allows arbitrary types. We consider that, in the firewall
verification, the high-abstractness of the semantics saved a lot of modeling and proving
effort which would have been taken in the case of using ACL2.
There are a lot of work to implement OO semantics in theorem provers especially
for Java and UML. The work by G. Klein et al. [6] implements semantics of Java for
both source language level and bytecode level in Isabelle/HOL. The work by G. Barthe
et al. [7] implements an executable semantics of JavaCard platform (virtual machine
and bytecode verifier) in Coq. Both of them adopt a deep embedding because their ver-
ification target is on the platform level such as type safety, soundness of Hoare calculi
and correctness of the bytecode verifier. We adopted a shallow embedding because our
verification target is on the instance level such as method contracts and class invariants.
A shallow embedding makes the proof on the instance level easier and the theory it-
self simpler than deep embedding. The work by J. Berg et al. [10] and C. March´e et
al. [11] implements Java semantics for reasoning Java programs annotated with JML
specifications as memory models in WHY and Isabelle/HOL, respectively. We defined
a similar memory model, but it differs from them in that it allows arbitrary types for ob-
ject attributes, which is effective in the verification on the analysis level. As for UML,
the work by [12] implements a semantics of UML sequence diagrams in PVS. The
work by A. D. Brucker et al. [13] implements a semantics of the specification language
OCL as a conservative shallow embedding in Isabelle/HOL. Compare to these work,
our semantics is not specific to particular languages but implements basic typical OO
concepts. We are aiming at constructing a general-purpose semantics which can be used
as a groundwork for various languages.
79

8 Conclusions and Future Work
In this paper, we presented an executable semantics of OO models for the foundation of
both simulation and theorem proving. The semantics is implemented in two languages:
HOL for theorem proving and ML for simulation. We preserved the semantics equiv-
alence between them by implementing the underlying heap memory structure within
the expressive intersection of HOL and ML. We also presented a verification system
ObjectLogic which supports simulation and theorem proving based on the executable
semantics. As an application, we showed a verification of a UML model of a practical
firewall server system. Future work is to reinforce the verification capability of Object-
Logic by implementing a test suite generator and a verification condition generator.
References
1. OMG. Unified Modeling Language. URL: http://www.omg.org/.
2. The HOL system. URL: http://hol.sourceforge.net/.
3. Moscow ML. URL: http://www.dina.dk/ sestoft/mosml.html.
4. J. Warmer and A. Kleppe. The Object Constraint Language: precise modeling with UML.
Addison-Wesley, 1999.
5. Tobias Nipkow, David von Oheimb and Cornelia Pusch. µJava: Embedding a Programming
Language in a Theorem Prover. In Foundations of Secure Computation. IOS Press, 2000.
6. Gerwin Klein et al. Bali project, http://isabelle.in.tum.de/Bali/
7. G. Barthe, G. Dufay, L. Jakubiec, S. Melo de Sousa, and B. Serpette. A Formal Exe-
cutable Semantics of the JavaCard Platform. In D. Sands, editor, Proceedings of ESOP’01,
http://citeseer.ist.psu.edu/470034.html
8. P. S. Rajan. Executing HOL specifications: Towards an evaluation semantics for classical
higher order logic. In L. J. M. Claesen and M. J. C. Gordon, editors, Higher order Logic
Theorem Proving and its Applications, Leuven, Belgium, September 1992. Elsevier.
9. S. Berghofer and T. Nipkow. Executing Higher Order Logic. In P. Callaghan, Z. Luo, J.
McKinna, and R. Pollack, editors, Types for Proofs and Programs (TYPES 2000), volume
2277 of LNCS. Springer-Verlag, 2002.
10. J. van den Berg, M. Huisman, B. Jacobs, and E. Poll. A type-theoretic memory model for
verification of sequential Java programs. Techn. Rep. CSI-R9924, Comput. Sci. Inst., Univ.
of Nijmegen, 1999.
11. Claude March´e and Christine Paulin-Mohring. Reasoning on Java programs with aliasing
and frame conditions. In 18th International Conference on Theorem Proving in Higher Order
Logics (TPHOLs 2005), LNCS, August 2005.
12. Demissie B. Aredo. A Framework for Semantics of UML Sequence Diagrams in PVS. Jour-
nal of Universal Computer Science (JUCS), 8(7), pp. 674-697, July 2002.
13. A. D. Brucker and B. Wolff. A proposal for a formal OCL semantics in Isabelle/HOL.
TPHOLs 2002, LNCS 2410, pp.99-114, 2002.
14. G. Al Sammane, J. Schmaltz, D. Toma, P. Ostier, D. Borrione. Theosim: Combining Sym-
bolic Simulation and Theorem Proving for Hardware Verification. Proc. of the 17th Sympo-
sium on Integrated Circuits and System Design (SBCCI’04), 2004.
15. Matthew Wilding, David Greve, David Hardin, Efficient Simulation of Formal Processor
Models, Formal Methods in Systems Design, 18(3), Kluwer Academic Publishers, May
2001.
16. Kenro Yatake, Toshiaki Aoki and Takuya Katayama. Implementing application-specific
Object-Oriented theories in HOL. In Proceedings of the 2nd International Conference on
Theoretical Aspects of Computing (ICTAC’05), pp.501-516, 2005.
80
