Employing Wavelet Transforms to Support
Content-Based Retrieval of Medical Images
Carolina W. da Silva, Marcela X. Ribeiro, Agma J. M. Traina and Caetano Traina Jr.
Computer Science Department, University of S˜ao Paulo at S˜ao Carlos
Cx. Postal 668, CEP 13560-970 , S˜ao Carlos, SP, Brazil
Abstract. This paper addresses two important issues related to texture pattern
retrieval: feature extraction and similarity search. We use discrete wavelet trans-
forms to obtain the image representation from a multiresolution point of view.
Features of approximation subspaces compose the feature vectors, which suc-
cinctly represent the images in the execution of similarity queries. Wavelets and
multiresolution method are used to overcome the semantic gap that exists be-
tween low level features and the high level user interpretation of images. It also
deals with the “curse of dimensionality”, which involves problems with a similar-
ity definition in high-dimensional feature spaces. This work was evaluated with
two different image datasets and the results show an improvement of up to 90%
for recall values up to 65%, in the query results using the Daubechies wavelet
transform when comparing to other wavelets and gray level histograms.
1 Introduction
Content-based image retrieval (CBIR) is a technology that employs methods and algo-
rithms aiming at accessing pictures by referencing image patterns rather than alphanu-
merical indices. In order to allow a fast query answer, representative numerical features
that serve as image signatures are extracted from each image in the repository. Then,
the images are indexed using these precomputed signatures. In the query execution, the
signature extracted from the query example is compared to the signature precomputed
from all images in the database [1].
Techniques for content-based access into medical image repositories are a subject
of high interest in recent research, and remarkable efforts have been reported so far. In
particular, CBIR for picture archiving and communication systems (PACS) can make a
significant positive impact in health informatics and health care. However, in spite of
the reports of innovations, the practical use of CBIR in PACS has not been established
yet. The reasons are manifold, and they are identified only informally, without an ob-
jective measure for evaluating the CBIR systems and identifying the shortcomings (or
gaps) in the methods. In general, two gaps have been identified in CBIR techniques:
(i) the semantic gap between the low-level features (color, texture and shape) that are
automatically extracted by machine and the high-level concepts of human vision and
⋆
We are thankful to FAPESP, CNPq and CAPES.
W. da Silva C., X. Ribeiro M., J. M. Traina A. and Traina Jr. C. (2008).
Employing Wavelet Transforms to Support Content-Based Retrieval of Medical Images.
In Proceedings of the 8th International Workshop on Pattern Recognition in Information Systems, pages 19-28
Copyright
c
 SciTePress

image understanding; and (ii) the sensory gap between the object in the world and the
information in a (computational) description derived from a recording of that scene [1].
Basically, all systems use the assumption of equivalence of an image and its rep-
resentation in the feature space. These systems often use measurement systems, such
as the easily understandable Euclidean vector space model for measuring distances be-
tween a query image (represented by its features) and possible results, representing
all images as feature vectors in an n-dimensional vector space. Nevertheless, metrics
have been shown to not correspond well to the human visual perception. Several other
distance measures do exist for the vector space model such as the city-block distance,
the Mahalanobis distance or a simple histogram intersection. Still, the use of high-
dimensional feature spaces has shown to cause problems. Also, caution should be taken
when choosing the distance measure in order to retrieve meaningful results. These prob-
lems with a similarity definition in high-dimensional feature spaces is also known as the
“curse of dimensionality”, and has also been discussed in the domain of medical imag-
ing [2].
Beyer et. al. proved in [3] that the increasing in the number of features (and con-
sequently in the dimensionality of the data) leads to losing the significance of each
feature value. Thus, to avoid decreasing the discrimination accuracy, it is important to
keep the number of features as low as possible, establishing a trade-off between the
discrimination power and the feature vector size.
Aimed at overriding the problems of the semantic gap and the “curse of dimension-
ality”, this paper shows a simple but powerful feature extractor based on multiresolution
wavelet transforms, which uses the approximation subspace to compose the feature vec-
tor to represent the image. The results of applying our method achieves 90% regarding
the precision in the retrieval of medical images that asks up to 65% of the image set.
2 Background - Wavelets
Our proposed technique works on image subspaces generated by applying wavelet
transforms through the multiresolution method. Wavelets are mathematical functions
that separate the signal in different components of frequency, and then examine each
component with a combined resolution with its scale.
It is interesting to compare the wavelet transform to the Fourier transform. While the
Fourier transform analyzes a signal according to the frequency, the wavelet transform
analyzes it according to the scale. Thus, the wavelets can remove statistical redundancy
among pixels, providing a more compact representation of the image information. It is
believed that image indexing generated over the wavelet transformed domain are more
efficient than those designed over the spatial domain. This is due to the fact that the
transformed coefficients have better defined distributions than image pixels. Besides,
the wavelets have a multiresolution property that make it easier to extract the image
features from transformed coefficients [4].
The central element of a multiresolution analysis is a function φ(t), called the scal-
ing function, whose role is to represent a signal at different scales. The translations of
the scaling function constitute the “building blocks” of the representation of a signal at

a given scale. The scale can be increased by dilating (stretching) the scaling function or
decreased by contracting it.
The scaling function φ(t) acts as a sampling function (a basis), in the sense that
the inner product of φ(t) with a signal represents a sort of average value of the signal
over the support (extent) of φ. A recursive application of this process generates new
nested spaces V
j
, that is, ...V
−2
⊂ V
−1
⊂ V
−0
⊂ V
1
⊂ ..., which are the basis of the
multiresolution analysis.
By definition, a signal in V
−1
can be expressed as a superposition of translations of
the function φ
1
, but since the space V
0
is included in V
−1
, any function in V
0
can also
be expanded in terms of the translations of φ(t). In particular, this is true for the scaling
function itself.
Consequently, there must exist a sequence of numbers h = h
0
, h
1
, . . . such that the
following relationship is satisfied :
φ
0
(t) =
X
n
h
n
φ
−1
(t −
n
2
) (1)
Equation 1 is very important and it is known as the scaling equation. Equation 1
describes how the scaling function can be generated by superposing compressed copies
of itself. Now it is possible to define a new space W
j
as the orthogonal complement of
V
j
in V
j+1
. In other words, W
j
is the space of all functions in W
j
that are orthogonal
to all functions in V
j
under the chosen inner product. The relationship to wavelets is in
the fact that the spaces W
m
are spanned by dilation and translation of a function ψ(t),
thus, such collection of basis functions are called wavelets.
As in the case with the scaling function, since the wavelet ψ(t) belongs to V
−1
, it
can be expressed as a linear combination of φ(t) at scale m = −1, which can be written
as:
ψ(t) =
X
n
g
n
φ
−1
(t − n) (2)
where the sequence g is called the wavelet sequence. In the literature, h and g are known
as the low and high frequency filters respectively.
Different wavelet bases are obtained by varying the support width of the wavelet. In
general, changes in the wavelet support affect the final frequency characteristics of the
wavelet transform. Usually the amplitudes of the coefficients change and, consequently,
the scale, where the signal and noise separate, also changes. The choice of a wavelet
basis still represents an open problem for filtering.
Probably the most popular wavelets are the Daubechies wavelets, because of their
orthogonality and compact support [5]. We choose Symlets, Coifman and Daubechies
wavelets to explore in this work.
3 Proposed Method
Our method deals with two inherent drawbacks of a CBIR system, the high dimension-
ality of feature vectors and the semantic gap. We amend the first one by applying higher

resolution on the multiresolution technique, and the second one by characterizing im-
ages through the feature vectors composed of the approximation subspace, which are
obtained through a convolution over each image by the wavelet filters. We choose the
following wavelet filters: Coifman (coif 1 and coif2), Symlet (sym2, sym3, sym4,
sym5 and sym15) and Daubechies (db1, db2, db3, db4 and db8)
1
.
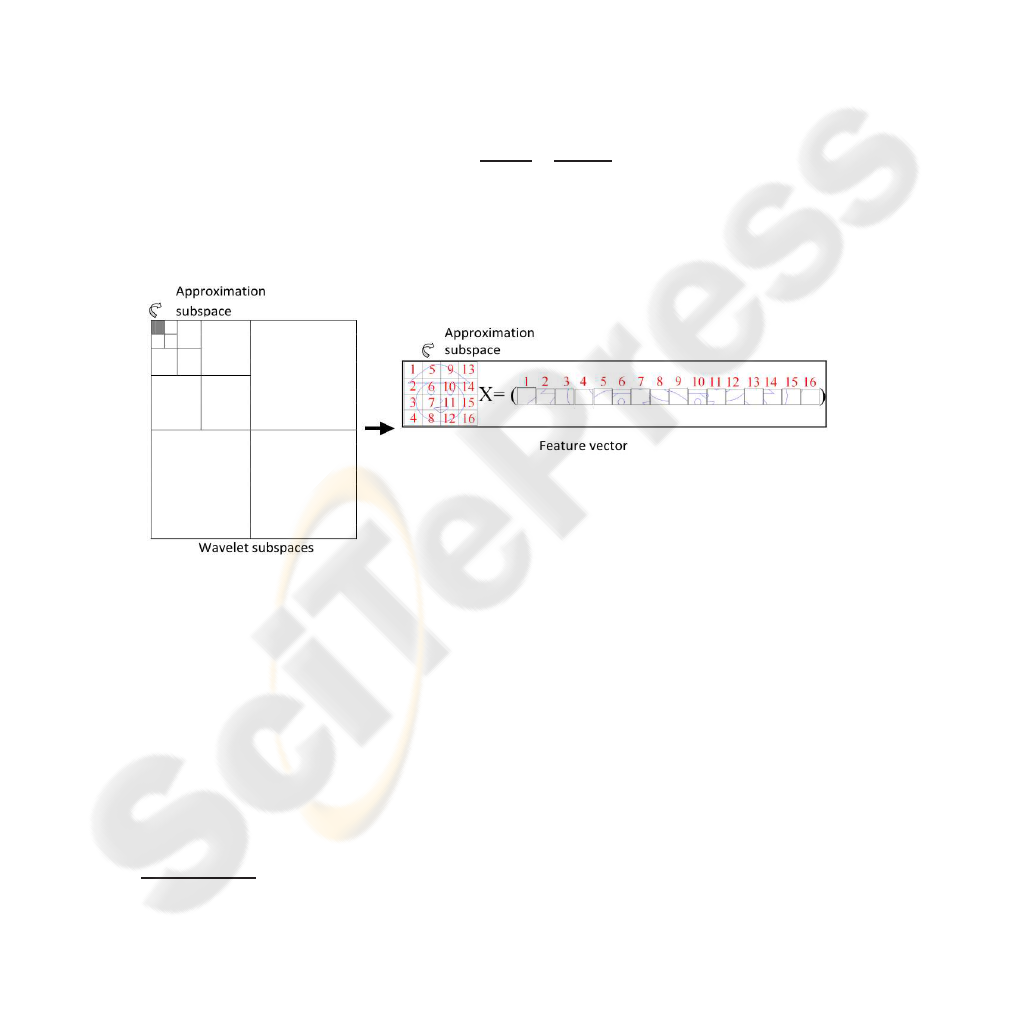
Figure 1 graphically summarizes the proposed method. We use 4, 5 and 6 levels
of resolution and the approximation subspace is represented by reading it column to
column, putting the values obtained on the feature vector. Thus, the dimension of the
feature vector is given by multiplying the dimension of the approximation subspace.
That is, to calculate the dimension of the feature vector we just divide by two the width
and the height of the image from each resolution level applied, as is shown in Figure 2,
and multiplying the dimensions of the approximation subspace. The Equation 3 gives
the formula to calculate the number of elements of the proposed feature vector.
#features =
width
2
N
∗
height
2
N
, (3)
where width is the image width, height is the image height and N is the level of decom-
position. Figure 2 shows an example of a wavelet decomposition and the configuration
of regions after decomposition.
Fig.1. Proposed method of feature extraction using 4 levels of decomposition. Each pixel value
of the approximation subspace is put in a feature vector.
For instance, if an image has 256 × 256 pixels, when it is applied 4 levels of reso-
lution, the feauture vector has 256 features, when it uses 5 levels, the feature vector has
64 features. And when it uses 6 levels, the feature vector has 16 features, which is the
total of pixels from the approximation subspace.
4 Experiments and Results
Using the proposed method, we developed a prototype to process k-nearest neighbor
queries (k-NN), answering queries such as: “retrieve the ten most similar images of the
1
These respectively wavelet filters can be found on the Matlab6.5 tool

(a) (b) (c)
Fig.2. Example of wavelet decomposition (a) original image; (b) image decomposed in two steps
from Haar wavelets; (c) configuration of regions after decomposition.
image MR Head of John Doe”. Figure 3 shows an example of a k-NN query performed
by our prototype. The similarity between two images is expressed by the distance be-
tween their respective feature vectors. We use the well-known Euclidean distance func-
tion (L
2
) to compare the feature vectors.
Query image Thumbnails of the 10 nearest neighbors
2439.jpg
Fig.3. Example of a 10-nearest neighbor query performed by the developed prototype over an
image database of 704 images.
In order to evaluate the effectiveness of the proposed technique we worked on a
variety of medical images categories, and the Precision and Recall (PR) graph [6] was
used as an efficacy measure, since it has been broadly employed to express the re-
trieval efficiency of a method. Recall indicates the proportion of relevant images in the
database that has been retrieved when answering a query, and Precision is the portion
of the retrieved images that are relevant for the query. As a rule of thumb, the closer the
PR curve to the top of the graph, the better the technique is. For our experiments, each
PR curve represents the average curve of all the curves obtained by performing a k-NN
query for each image in the whole images set.
We have used the Slim-tree [7] as the indexing structure for the prototype, which is
a metric access method (MAM) specially developed to minimize disk accesses, making
the whole system faster.
4.1 Experiment 1 - The 210 Images Dataset
This dataset consists of 210 medical images classified in seven categories: Angiogram,
MR (Magnetic Resonance) Axial Pelvis, MR Axial Head, MR Coronal Abdomen, MR

Coronal Head, MR Sagittal Head and MR Sagittal Spine. Each category is represented
by 30 images.
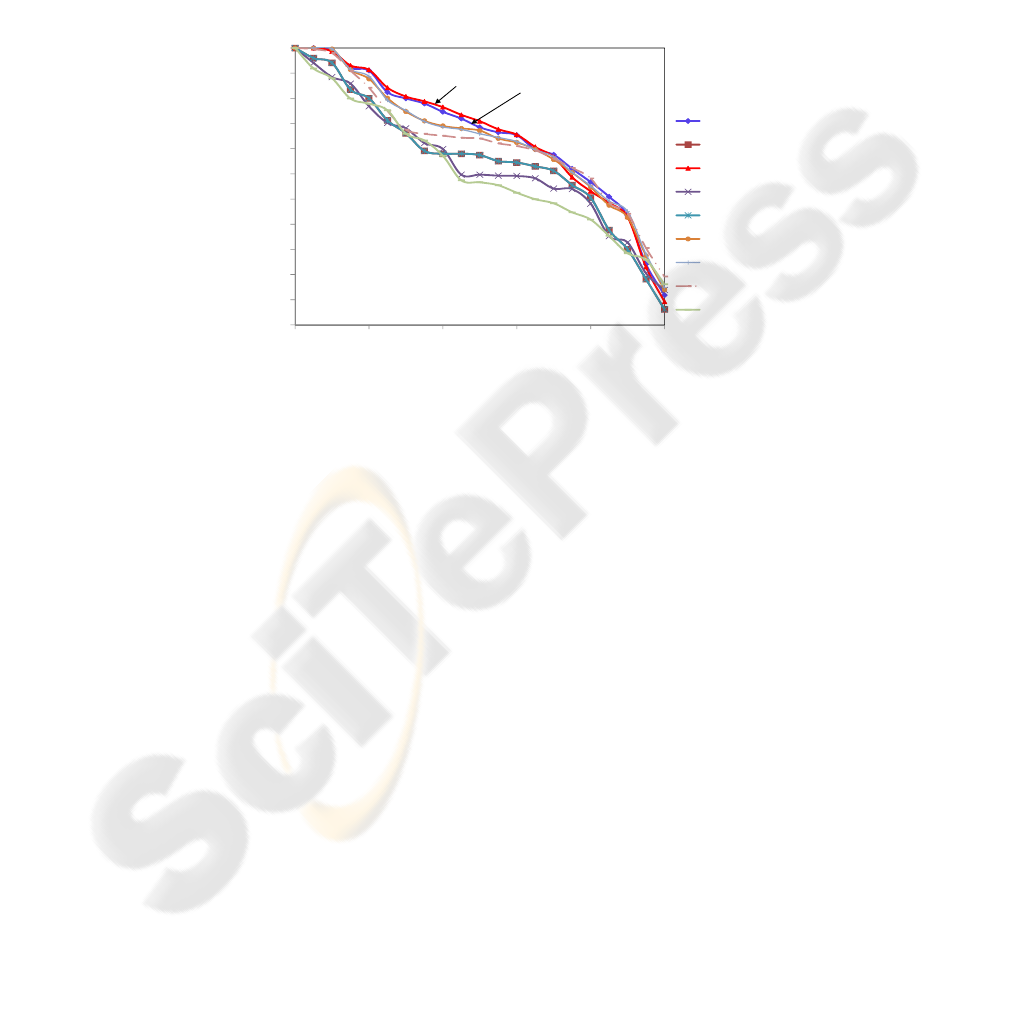
First, we compare the method by using 4 levels of resolution and Coifman (coif 1
and coif 2) , Daubechies (db2 and db8) and Symlet (sym2, sym3, sym4, sym5 and
sym15) wavelets. The use of each one of these wavelet transforms generate a vector
with 256 features. The PR curves of the nine proposed vectors are shown in Figure 4.
Each point of the graph is obtained by the average of 210 queries.
0.75
0.8
0.85
0.9
0.95
1
s
ion
PrecisionXRecall
coif1
coif2
db2
db2
coif1
0.45
0.5
0.55
0.6
0.65
0.7
0 0.2 0.4 0.6 0.8 1
Preci
s
Recall
db8
sym2
sym3
sym4
sym5
sym15
Fig.4. PR curves showing the retrieval behavior of the proposed method using the 4
th
level of
resolution, with 256 features.
Analyzing the graphs of Figure 4, we can see that the wavelet that best represents
the images is the Daubechies db2. We can also consider that the curve generated by
coif1 wavelet practically ties to db2.
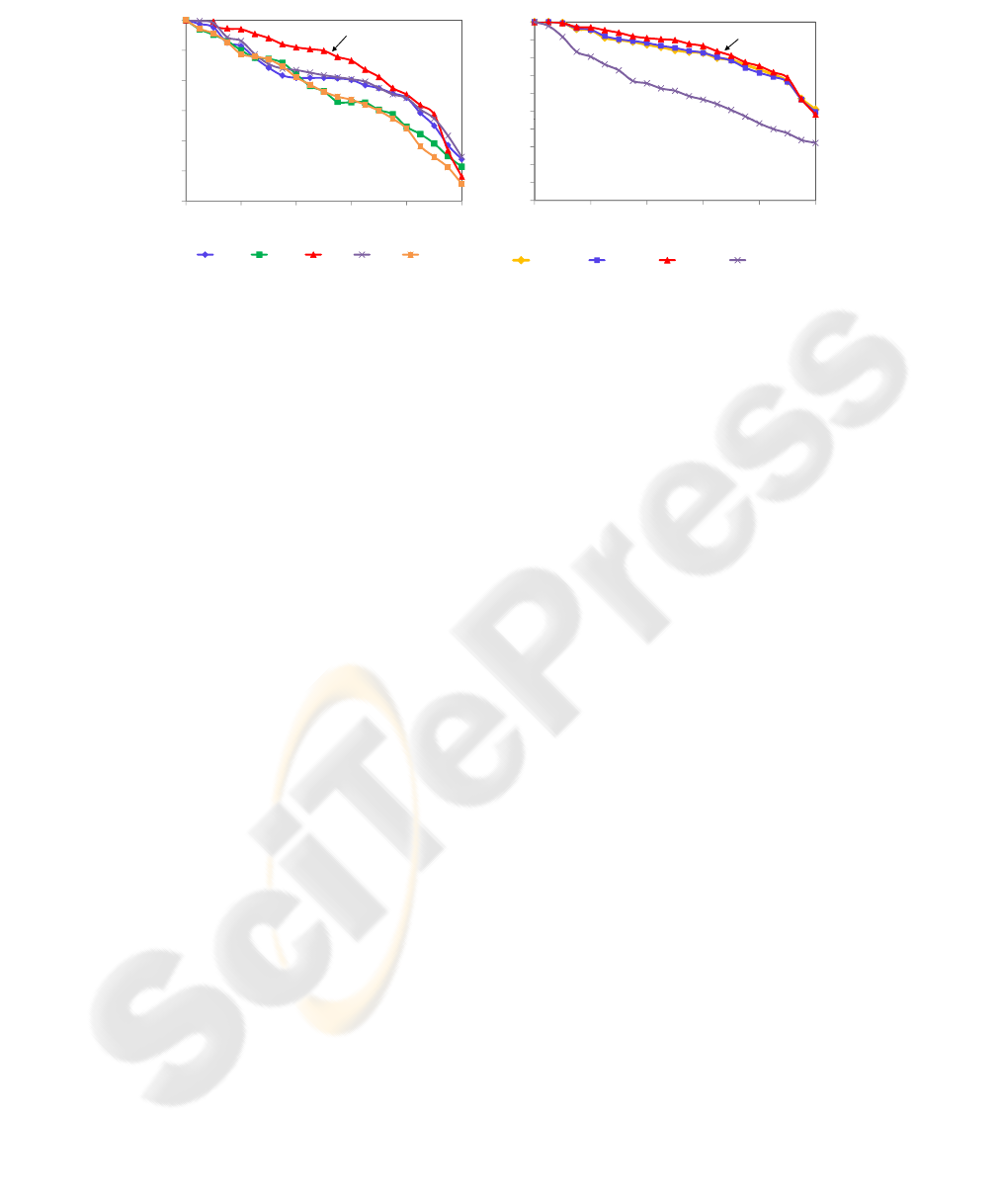
For the graphics in Figure 5, we compare the Coifman (coif 1 and coif 2) and
Daubechies (db1, db2 and db8 ) wavelet transforms in the 5
th
level of resolution. Thus,
their feature vectors also have 64 features. Figure 5 shows the PR curves from the
queries on the dataset represented by these feature vectors.
Note that the Haar (or db1) wavelet is the best one to represent these images. As
a basis for comparison, the graphs in Figure 6 also presents the average PR curve ob-
tained by using gray-level histograms over the same image dataset. The results for Haar
(or db1) give the best PR curves shown until now. We can see that all the proposed
methods have better PR curves than Histogram. The curve with better precision is the
one generated by db1, with just 64 features, while the other methods use 256 features,
i.e., there is a reduction of 75% on the data dimensionality. The queries performed by
using the db1 feature vectors taken from the 5
th
level of resolution give precision rates
up to 82,55% regarding the images’ histogram, to queries that ask until 90% of the im-
ages. These methods are well-suited to represent the images under evaluation, since the
precision values are over than 80% for all recall values less than 65%.

0.7
0.8
0.9
1
cision
PrecisionXRecall
db1
0.4
0.5
0.6
0 0.2 0.4 0.6 0.8 1
Pre
Recall
coif1 coif2 db1 db2 db8
Fig.5. PR curves showing the retrieval behav-
ior of the proposed method using the 5
th
level
of resolution, with 64 features.
0.5
0.6
0.7
0.8
0.9
1
e
cision
PrecisionXRecall
db1-5n
0
0.1
0.2
0.3
0.4
0 0.2 0.4 0.6 0.8 1
Pr
e
Recall
coif1Ͳ4n db2Ͳ4n db1Ͳ5n histogram
Fig.6. PR curves showing the retrieval be-
havior of the best curves and gray-level his-
tograms.
Thus, we can conclude that the dimensionality curse really damages the results,
because the irrelevant features disturb the influence of the relevant ones. Moreover, the
application of wavelet transform in 5 levels through the multiresolution method reduced
the redundancy of information from data, and it also well represents the images for
executing similarity queries.
4.2 Experiment 2 - The 704 Image Dataset
A larger image dataset, with 704 MR images, which is classified in eight categories was
used herein. The number of the images in the dataset regarding each category is: An-
giogram (36), MR Axial Pelvis (86), MR Axial Head (155), MR Sagittal Head (258),
MR Coronal Abdomen (23), MR Sagittal Spine (59), MR Axial Abdomen (51) and MR
Coronal Head (36). In the previous experiment the best result was obtained applying
a Daubechies wavelet transform, and, according to Wang [8], the Daubechies wavelet
achieves excellent results in image processing due to its properties. Thus, we use sev-
eral wavelets of the family of Daubechies on 4, 5 and 6 levels of resolution by the
multiresolution method.
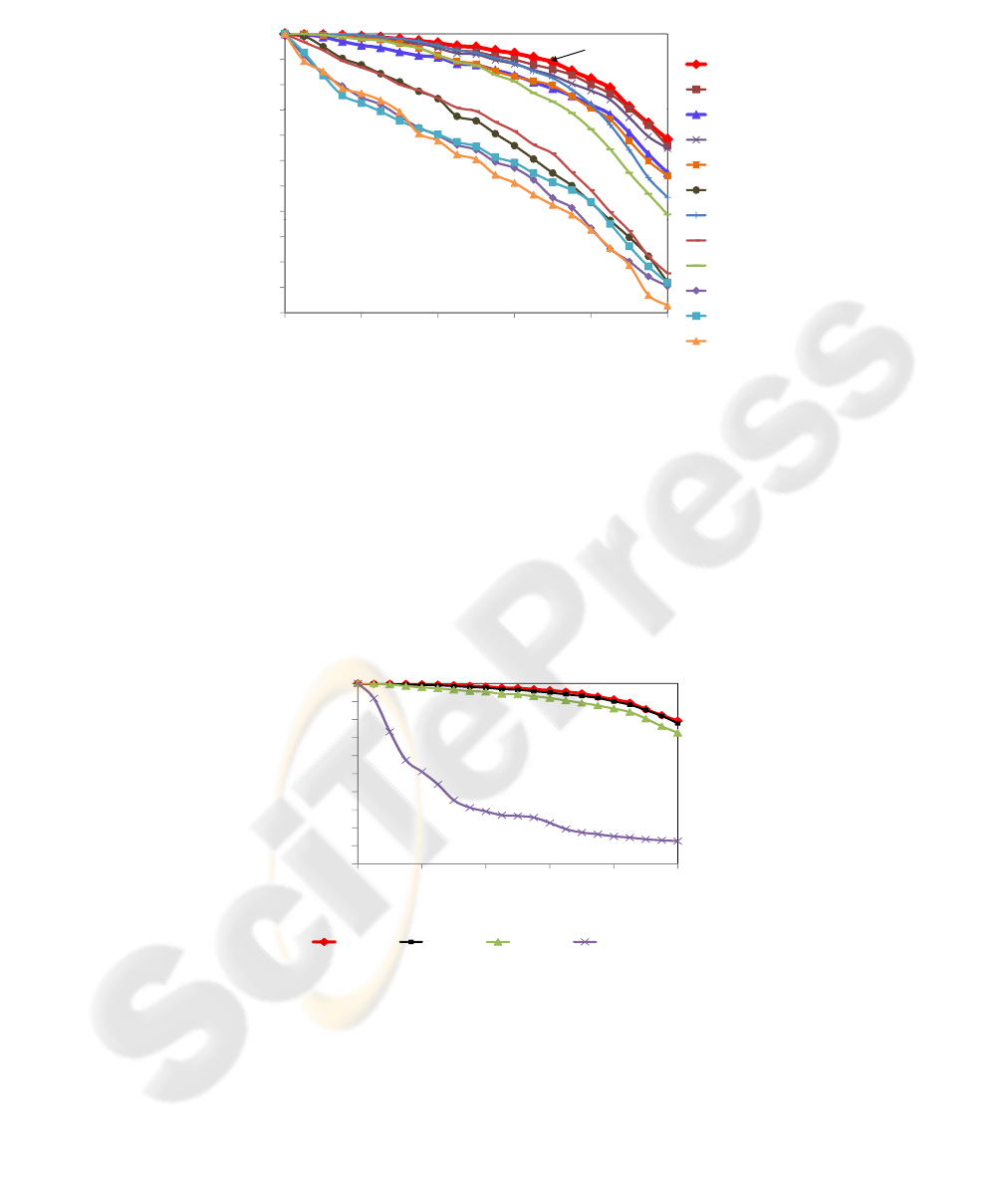
Figure 7 shows the Precision vs. Recall generated by the proposed method. First,
it is displayed the wavelet name, then the level of resolution and finally the number
of elements of the feature vector. Observe that the PR curves generated by the same
wavelet transform in several levels of resolution decrease according to the wavelet cho-
sen. The bigger the number of the filters, the faster the curves decrease when a higher
level of resolution is chosen. Analyzing the db1 wavelet, which has two filters, observe
that the curves generated in 4 and 5 levels of resolution are equivalent, even exiting a
large difference between the number of features from their vectors. For a 6 level of res-
olution we still have an excellent result (see db1-6n-16 curve), as with just 16 features,
the precision is over than 80% for values of recall until 90%. And comparing the 256
features with the 16 ones, we have a dimensionality reduction of 93.75%. Also note that
the larger the number of filters, the smaller the precision of the queries, considering the
same level of resolution.

0 95
1
PrecisionXRecall
db1-4n
0 85
0.9
0
.
95
db1Ͳ4n
db1Ͳ5n
db1
6
0.75
0.8
0
.
85
ion
db1
Ͳ
6
n
db2Ͳ4n
db2
5n
0.65
0.7
0.75
Precis
db2
Ͳ
5n
db2Ͳ6n
db3Ͳ4n
0.55
0.6
db3Ͳ5n
db4Ͳ4n
0.45
0.5
db4Ͳ5n
db8Ͳ4n
0 0.2 0.4 0.6 0.8 1
Recall
db8Ͳ5n
Fig.7. PR curves generated by several Daubechies wavelets transforms using the 4
th
, 5
t
h and
6th level of multiresolution.
Figure 8 shows the best curves of PR with 256, 64 and 16 features, respectively,
from the Figure 7 and compare them with the curve given by the gray-level histogram.
Visually, all three methods have a better performance than the histogram. Numerically,
we get an improvement of precision until 531% to values of recall until 95%, for the
feature vector with 256 features. For 64 features, the improvement in precision is up
to 528% to a recall of 95%; and for 16 features, the improvement in precision is up to
491% to a recall of 90%.
0.5
0.6
0.7
0.8
0.9
1
e
cision
PrecisionXRecall
0
0.1
0.2
0.3
0.4
0 0.2 0.4 0.6 0.8 1
Pr
e
Recall
db1Ͳ4n db1Ͳ5n db1Ͳ6n histogram
Fig.8. PR curves showing the retrieval behavior of the best curves and gray-level histogram.
To compare this method with another one from literature, we used a technique pro-
posed by Balan [9], which employs an improved version of the EM/MPM method to
segment images, and for each region segmented based on texture, six features were ex-

tracted: the mass (m); the centroid (xo and yo); the average gray level (µ), the Fractal
dimension (D); and the linear coefficient used to estimate D (b). Therefore, when an
image is segmented in L classes, the feature vector has L * 6 elements. Here we use
L = 5, so the feature vector has 30 features. Figure 9 illustrates the feature vector
described.
D
1
x0
1
y0
1
m
1
µ
1
b
1
... D
L
x0
L
y0
L
m
L
µ
L
b
L

Featuresofthetextureclass1 FeaturesofthetextureclassL
Fig.9. The feature vector.
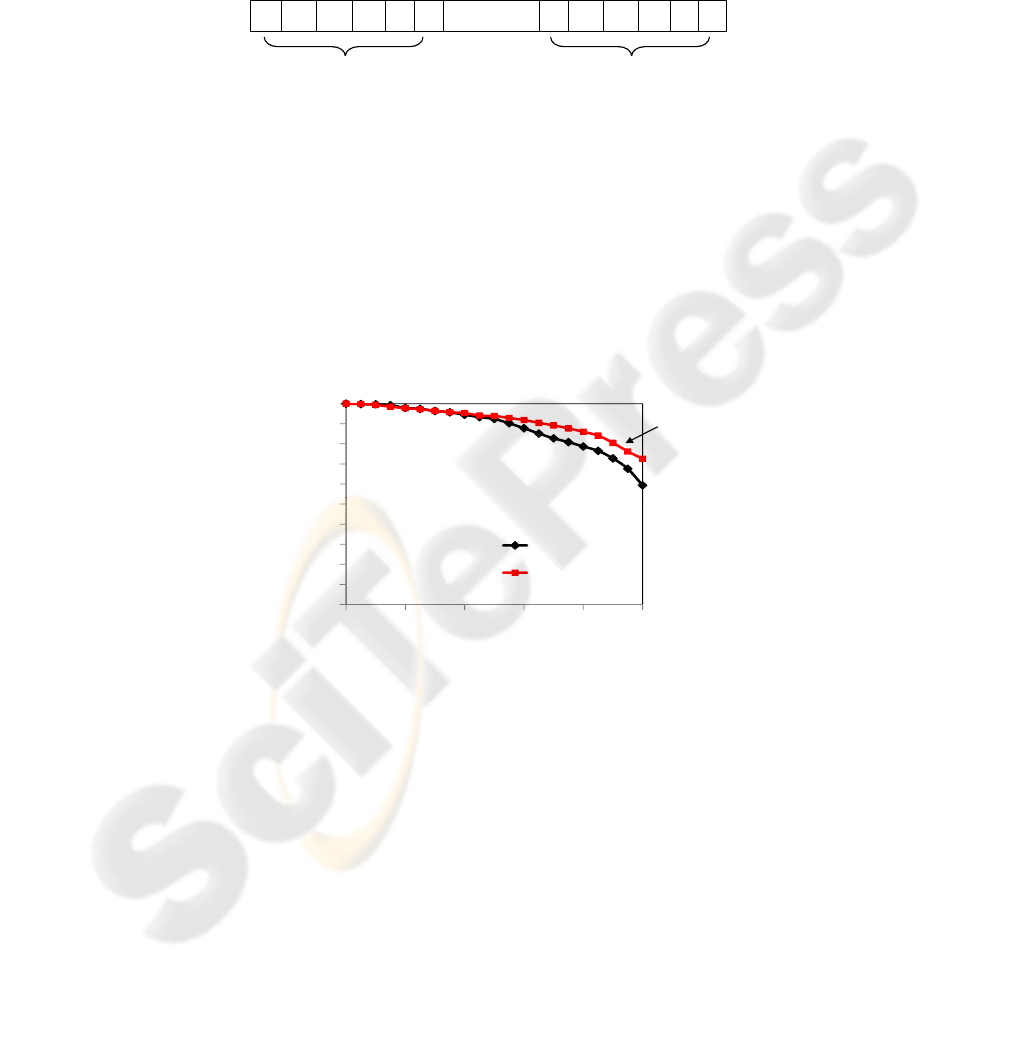
Figure 10 shows the comparison of the curves generated by our method with 16
features (db1-6n-16 curve) to the method that uses an improved version of EM/MPM
algorithm, which is one of the best methods in the literature. We can see that our method
performs better when processing similarity queries (k-NN). Note also that our method
demands fewer features than EM/MPM. We can also compare the time spending to im-
age processing and extraction of the features. While the improved version of EM/MPM
spends around 17.05 seconds per image, our method with 16 features spends around
0.77 seconds.
0
0.6
0.7
0.8
0.9
1
s
ion
PrecisionXRecall
db1-6n
0
0.1
0.2
0.3
0.4
0
.5
0 0.2 0.4 0.6 0.8 1
Preci
s
Recall
30features
16features
Fig.10. PR curves from db1-6n with 16 features and from improved version of the EM/MPM.
5 Conclusions
In this paper we presented a new technique based on wavelet-approximation subspaces,
which was used to compose the image feature vector to process similarity queries on
the image content. A tool based on the presented technique was implemented, aimed at
validating the technique proposed on real images from different tissues of the human
body, and to assist the study and analysis of medical images. Thus, the method can be
included in a PACS under development in our institution.

Several wavelets were evaluated, and the Daubechies showed a better efficacy than
the other ones for the analyzed image sets. The achieved results showed that the pro-
posed method performs very well, presenting an image retrieval accuracy always over
90% for recall values smaller than 65%. Moreover, we obtained a feature vector with
just 16 elements that provided a better performance than the feature vector with 30 fea-
tures obtained from segmented images by using an improvement version of EM/MPM
algorithm, which is a much more time consuming method. By the results obtained in
the work, we can claim that wavelets and the multiresolution method are well suited to
deal with the issue of the semantic gap and the dimensionality of feature vectors.
References
1. Deserno, T.M., Antani, S., Long, L.R.: Gaps in content-based image retrieval. In: Medical
Imaging 2007: PACS and Imaging Informatics. Volume 6516 of SPIE. (2007)
2. M¨uller, H., Michoux, N., Bandon, D., Geissbuhler, A.: A review of content-based image
retrieval systems in medical applications-clinical benefits and future directions. International
Journal of Medical Informatics 73 (2004) 1–23
3. Beyer, K., Godstein, J., Ramakrishnan, R., Shaft, U.: When is “nearest neighbor” meaningful?
In: ICDT. Volume 1540 of Lecture Notes in Computer Science. (1999) 217–235
4. Stollnitz, E.J., DeRose, T.D., Salesin, D.H.: Wavelets for Computer Graphics - Theory and
Applications. (1996)
5. Daubechies, I.: Ten Lectures on Wavelets. Volume 61. (1992)
6. Baeza-Yates, R.A., Ribeiro-Neto, B.A.: Modern Information Retrieval. (1999)
7. Traina Jr., C., Traina, A.J.M., Seeger, B., Faloutsos, C.: Slim-trees: High performance metric
trees miniminzing overlap between nodes. Research Paper CMU-CS-99-170 (1999)
8. Wang, J.Z.: Wavelets and imaging informatics: A review of the literature. Journal of Biomed-
ical Informatics 34 (2001) 129–141
9. Balan, A.G.R., Traina, A.J.M., Traina Jr., C., Marques, P.M.d.A.: Fractal analysis of image
textures for indexing and retrieval by content. In: 18th IEEE CBMS. (2005) 581–586