MULTICRITERIA DECISION SUPPORT SYSTEM

MULTIOPTIMA

Mariana Vassileva, Vassil Vassilev, Boris Staykov, Krassimira Genova

Department of Decision Support Systems, Institute of Information Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev Str., bl. 2, Sofia, Bulgaria

Danail Dochev

Department of Artificial Intelligence, Institute of Information Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev Str., bl. 2, Sofia, Bulgaria

Keywords: Multicriteria Decision Making, Multicriteria Decision Support System, Multicriteria Analysis, Multicriteria

Optimization, Interactive Method, Scalarizing Problem.

Abstract: The paper presents a multicriteria decision support system, called MultiOptima. It consists of two

independent parts - the MKA-2 system and the MKO-2 system. The MultiOptima system is designed to

support the decision maker in modelling and solving different problems of multicriteria analysis and linear

and linear integer problems of multicriteria optimization. The system implements four methods for

multicriteria analysis, as well as an innovative generalized interactive method for multicriteria optimization

with variable scalarization and parameterization, which can apply twelve scalarizing problems and is

applicable for different ways of defining preferences by the decision maker. The class of the solved

problems, the system structure, the implemented methods and the graphical user interface of the MKA-2

and MKO-2 systems are discussed in the paper. The MultiOptima system can be used both for education

and for solving of real-life problems.

1 INTRODUCTION

Multicriteria decision making problems are weak

formalized problems, the solution of which requires

the participation of the so-called decision maker

(DM). The solutions obtained are to a great extent

subjective and depend on DM’s preferences.

Different problems of planning, control, analysis and

monitoring in economy, transport, industrial

production, education, ecology and other spheres

may be reduced to multicriteria decision making

problems. The multicriteria decision making

problems can be divided into two subclasses. In the

first class (the so-called problems of multicriteria

optimization) a finite number of explicitly set

constraints in the form of functions defines an

infinite number of feasible alternatives. In the

second class (the so-called problems of multicriteria

analysis) a finite number of alternatives is explicitly

given in a tabular form. In multicriteria analysis and

multicriteria optimization problems several criteria

are simultaneously optimized in the feasible set of

alternatives. In the general case, there does not exist

one alternative, which optimizes all the criteria.

There is a set of alternatives characterized by the

following property: each improvement in the value

of one criterion leads to deterioration in the value of

at least one other criterion. This set of alternatives is

called a set of the non-dominated or Pareto optimal

alternatives (solutions). Each alternative in this set

could be a solution of the multicriteria problem. In

order to select one alternative, it is necessary to have

additional information set by the DM.

Many real-life problems in management may be

formulated as problems of multicriteria analysis

(choice, ranking or sorting) of resources, strategies,

projects, offers, policies, credits, products,

innovations, designs, costs, profits, portfolios, etc.

(Paschetta and Tsoukiàs, 2000). Many real-life

problems in planning, control and industrial

production may be formulated as problems of

multicriteria optimization (Rajesh et al., 2001).

276

Vassileva M., Vassilev V., Staykov B., Genova K. and Dochev D. (2008).

MULTICRITERIA DECISION SUPPORT SYSTEM MULTIOPTIMA.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 276-281

DOI: 10.5220/0001698602760281

 SciTePress

Different methods have been developed to solve

multicriteria analysis problems. A great number of

the methods, developed up to now, can be grouped

in three separate classes. The first class of methods

(Dyer, 2004) includes the multiattribute utility

(value) theory methods (e.g., Value Tradeoff

Method, UTA method, MACBETH method, Direct

Weighting Method, and AHP weighting methods).

These methods are based on the assumption that

there does not exist limited comparability among the

alternatives. The second class of methods are called

outranking methods (e.g., ELECTRE methods

(Figueira et al., 2005), and PROMETHEE methods

(Brans and Mareschal, 2005)) and they are based on

the assumption that there exists limited

comparability among the alternatives. In these

methods one (or several) outranking relation(s) are

first built to aggregate DM's global preferences, after

which this outranking relation is used to assist the

DM in solving the multiple criteria decision analysis

problem. The interactive methods (e.g., RNIM

method (Narula et al., 2003)) belong to the methods

of the third group. They are “optimizationally

motivated” and are oriented to solve multicriteria

analysis problems with a large number of

alternatives and a small number of criteria.

There are two main approaches in solving

multicriteria optimization problems: the scalarizing

approach (Miettinen, 2003) and the approximation

approach (Ehrgott and Wiecek, 2005). Interactive

methods are the major representatives of the

scalarizing approach. Multicriteria optimization

problem is treated in these methods as a decision

making problem and the emphasis is put on the real

participation of the DM in the process of its solution.

The interactive methods are the most developed and

widespread due to their basic advantages – a small

part of the Pareto optimal solutions must be

generated and evaluated by the DM; in the process

of solving the multicriteria problem, the DM is able

to learn with respect to the problem; the DM feels

more confident in his/her preferences concerning the

final solution of the problem being solved.

The interactive methods of the reference point

(direction) and the classification-based interactive

methods (Vassileva, 2005) are the most widely

spread interactive methods when solving

multicriteria optimization problems. Though the

interactive methods of the reference point are still

dominating, the classification-based interactive

methods (e.g., GENWS-IM method (Vassileva,

2005)) enable the better solution of some important

problems in the dialogue with the DM, relating to

his/her preferences defining, and also concerning the

time of waiting for new non-dominated solutions

that are evaluated and selected.

A variety of methods to approximate the set of

Pareto optimal solutions of different types have been

proposed (Ehrgott and Wiecek, 2005). Their main

representatives are the multicriteria genetic

(evolutionary) methods (Deb, 2001). The

multicriteria optimization problem is treated in these

methods rather as a vector optimization problem,

than as a decision making problem.

The developed software systems supporting the

solution of multicriteria analysis and multicriteria

optimization problems may be classified in two

groups: software systems with general purpose and

problem-oriented software systems. The general-

purpose software systems aid the solution of

different multicriteria analysis or multicriteria

optimization problems by different decision makers.

The problem-oriented software systems serve to

support the solution of one or several types of

specific multicriteria analysis or multicriteria

optimization problems and very often are included in

other information-control systems.

The following general-purpose software systems

(Weistroffer et al., 2005) aid the solution of different

multicriteria analysis problems – VIMDA, Expert

Choice, PROMCALC, GAIA, ELECTRE III-IV,

MACBETH, VIP, Decision Lab, Web-HIPRE,

MultiChoice and KnowCube. One problem-oriented

multicriteria analysis system is the Agland Decision

System for agricultural property (Parsons, 2002).

Some well-known general-purpose multicriteria

optimization software systems (Weistroffer et al.,

2005) are the following: VIG, DIDAS, DINAS,

MOLP-16, LBS, SOMMIX, MOIP, WWW-

NIMBUS, MOLIP, NLPJOB and MOMILP. The

ADELAIS system for portfolio selection

(Zopounidis et al., 1998) is an attractive problem-

oriented multicriteria optimization system. In the

class of multicriteria optimization systems must also

be included software systems, which implement

different multicriteria evolutionary methods (e.g.,

MOSES system (Coello and Christiansen, 1999)).

The paper describes some basic elements of the

multicriteria decision support system MultiOptima,

which consist of two separate parts - the MKA-2

system and MKO-2 system. The system is designed

to support the DM in solving different multicriteria

analysis and multicriteria optimization problems.

The class of the solved problems, the system

structure, the operation with the interface modules

for entering the information about DM’s local

preferences and for visualization of the current and

277

MULTICRITERIA DECISION SUPPORT SYSTEM MULTIOPTIMA

final solutions, as well as the help information, given

in a digital and graphical form, are discussed.

The rest of the paper is organized as follows. The

second section describes the basic features of the

first part of the MultiOptima system - MKA-2

system. The main characteristics of the second part

of the MultiOptima system – MKO-2 system, are

presented in brief in the third section. Finally, the

conclusions are given in the last section.

2 MKA-2 SYSTEM

The MKA-2 system, which is the first part of the

MultiOptima system, operates under MS Windows

operating system and it is designed to support DM in

solving different multicriteria analysis problems.

The MKA-2 system consists of internal-system

modules, four solving modules and interface

modules. It is realised in MS Windows environment,

including the standard user interface elements. The

internal-system modules contain all global

definitions of variables, functions and procedures of

general purpose. The object possibilities of Visual

Basic are utilized in the MKA-2 system, creating the

following classes with respect to internal-system

structures: a class for messages, which encapsulates

the output of error messages, dynamic context help

information and logging events in the debug

window, localization and identification of errors

occurring during the system operation; a class matrix

with some specific procedures, necessary for the

AHP method; a class for storing the information

specific for the criteria in the ELECTRE III and

PROMETHEE II methods and a class for storing

elements of the RNIM interactive method history.

MKA-2 handles files with “*.mka” extension.

Standard operations for creating, editing, loading

and saving of files are implemented. The MKA-2

files contain input data and data related to the

process and the results from solving multicriteria

analysis problems.

The solving modules realize four methods - AHP

method, ELECTRE III method, PROMETHEE II

method and RNIM method, and procedures for

transformation of qualitative, ranking and weighting

criteria into quantitative criteria. The AHP method is

one of the most widely spread weighting methods.

Pair-wise criteria comparison is used in this method

to set DM’s preferences. On this basis, a pair-wise

comparison matrix is constructed. The estimates of

the weights can be found by normalizing the

eigenvector corresponding to the largest eigenvalue

of this matrix. The ELECTE III is one of the most

often used outranking methods. It is based on an

outranking relation, characterized by the definition

of an outranking degree S (a, b) associated with each

ordered pair (a, b) of alternatives, representing the

more or less great outranking credibility of a over b.

There are two matrix needed to be evaluated - the

concordance matrix (requires indifference and

preference thresholds) and the discordance matrix

(requires additional threshold, called veto threshold,

which allows the outranking relation to be rejected).

In order the degree of credibility of outranking to be

obtained, the two measures from concordance and

discordance matrix have to be combined. The

obtained credibility matrix is essential for generating

two distillation orders that show whether one

alternative outranks the other or such an alternative

is incomparable to the other. In order the final

ranking to be obtained, the two orders are combined.

The PROMETHEE II method is the other most often

used outranking method. The intensity of the

preference of one alternative over another regarding

each criterion is measured in terms of the so-called

preference function. Six types of preference

functions are used, formed on the basis of

indifference and preference thresholds. The method

provides a complete ranking of the alternatives

through a pair-wise dominance comparison of net

positive and net negative outranking flows. The

RNIM method is a representative of the interactive

methods and it is appropriate for solving

multicriteria analysis problems with a large number

of alternatives and a small number of criteria. The

DM can provide desired or acceptable levels,

directions and intervals of changes in the values of

the criteria at any iteration. On the basis of this

information, the method enables the use of discrete

optimization scalarizing problems, with the help of

which the DM has the possibility for a more

systematic and successful screening of the

alternatives set.

The interface modules ensure the interaction

between the MKA-2 system, DM and operating

system. This interaction includes the entry of the

data for the multicriteria analysis problem; entry of

specific information for every method; entry of

information about DM’s preferences; visualization

of the current and final results; graphical

presentation of the solutions; printing out, reading

and storing of files; multi-language support,

dynamic help, etc. The editing module enables

entering, alteration and storing of quantitative,

qualitative, ranking and weighting criteria. The

interface preference modules aid DM in the entry of

criteria pair-wise comparison information, inter- and

ICEIS 2008 - International Conference on Enterprise Information Systems

278

intra-criteria information and information about the

desired or acceptable levels, directions and intervals

of change in the values of the criteria. The current

and final results and the parameters for the separate

methods, selected by the DM, are presented digitally

and graphically with the help of visual interface

modules. The input/output interface modules enable

the reading and storing in files, the printing of the

current and final results obtained, as well as the

printing of the information, given by DM. The

solution process can be interrupted at any stage and

activated from the place of its interruption at any

time. The MKA-2 system has comparatively rich

printing functions – the entire process of decision

making is documented and could be printed out.

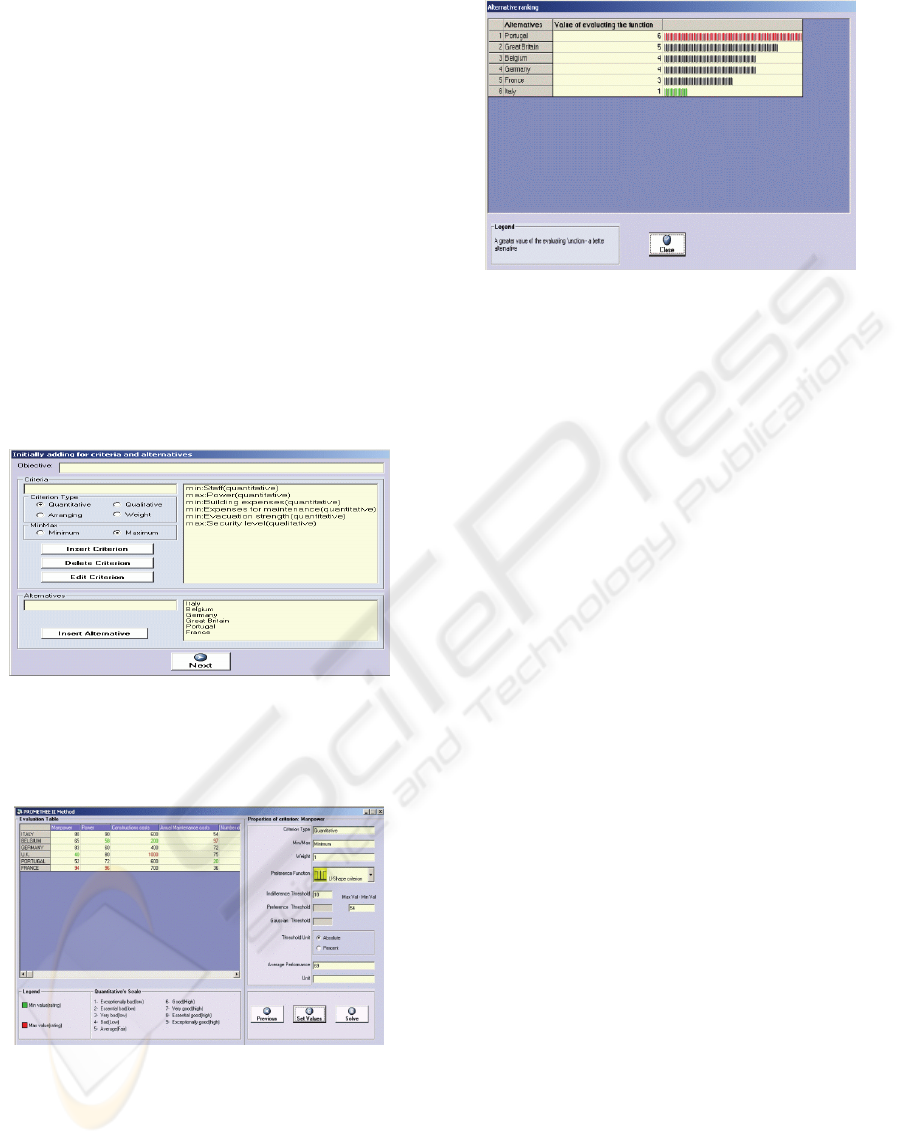
Figure 1 shows the initial information entered for

the real-life problem, concerning the choice of a

building site for new European electric power station

(Mladineo et al., 1987).

Figure 1: Initial information.

Figure 2 presents a window with information

about DM’s preferences in operation with the

PROMETHEE II method.

Figure 2: DM’s preferences in PROMETHEE II method.

Figure 3 shows the final result, obtained for six

countries when solving the ranking problem with the

ELECTRE ІІІ method.

Figure 3: The final result by ELECTRE ІІІ

method.

3 MKO-2 SYSTEM

The MKO-2 system, which is the second part of the

MultiOptima software system, operates also under

MS Windows operating system and it is designed to

aid the DM in the solution of linear and linear

integer problems for multicriteria optimization. The

system implements the innovative generalized

interactive method for multicriteria optimization

GENWS-IM (Vassileva, 2005) with variable

scalarization and parameterization, which can apply

twelve scalarizing problems and is applicable for

different ways of defining DM’s preferences.

The MKO-2 software system consists of three

main groups of modules – a control program,

optimization modules and interface modules. The

control program is integrated software environment

for creation, processing and storing of files

associated with MKO-2 system, as well as for

linking and executing of different types of software

modules. The basic functional possibilities of the

control program may be separated in three groups.

The first group includes the possibilities to use the

applications, menus and system functions being

standard for MS Windows (“File”, “Edit”, “View”,

“Window”, “Help”) in the environment of MKO-2

system. The second group of functional possibilities

encloses the control of the interactions between the

modules realizing the creation, modification and

storing of files associated with MKO-2 system,

which contain input data and data connected with

the process of interactive solution of linear and

linear integer multicriteria optimization problems, as

well as the localization and identification of the

errors occurring during the process of operation with

MKO-2 system. The third group of functional

possibilities of the control program includes the

possibilities for visualization of essential

279

MULTICRITERIA DECISION SUPPORT SYSTEM MULTIOPTIMA

information about the DM and information of the

system operation as a whole.

The optimization modules realize the generalized

interactive algorithm GENWS–IM, two simplex

algorithms solving continuous single-criterion

problems (Vanderbei, 1996), and an algorithm of

“branches and bounds” type solving linear integer

single-criterion problems (Wolsey, 1998).

The interface modules provide the dialogue

between DM and the system during the entry and

correction of the input data of the multicriteria

problems being solved, during the interactive

process of these problems solution, as well as for

dynamic numerical and graphical visualization of

the main parameters of the solving process. With the

help of an editing module the formulations of the

criteria and constraints are input, altered and stored,

and also the type and limits of the variables

alteration. Another interface module serves to supply

two types of graphic presentation of the information

about the values of the criteria at the different steps

of the solving process, as well as the possibilities for

their comparison.

One of the main functions of MKO-2 system is

to enable the extension of DM’s possibilities to set

his/her preferences with the help of criteria weights,

ε – constraints, desired and acceptable levels of

alteration in the criteria values, desired and

acceptable directions of change of the criteria

values, desired and acceptable levels, directions and

intervals of alteration of the criteria values. Twelve

scalarizing problems are generated in the MKO-2

system in order to realize these possibilities.

Depending on DM’s preferences, these scalarizing

problems are automatically generated by the

generalized scalarizing problem GENWS by

changing its structure and parameters.

The MKO-2 system presents to the DM different

windows intended for entry and correction of the

criteria and constraints of the multicriteria problem

being solved, for setting his/her preferences, for

choosing the solving method and for visualizing the

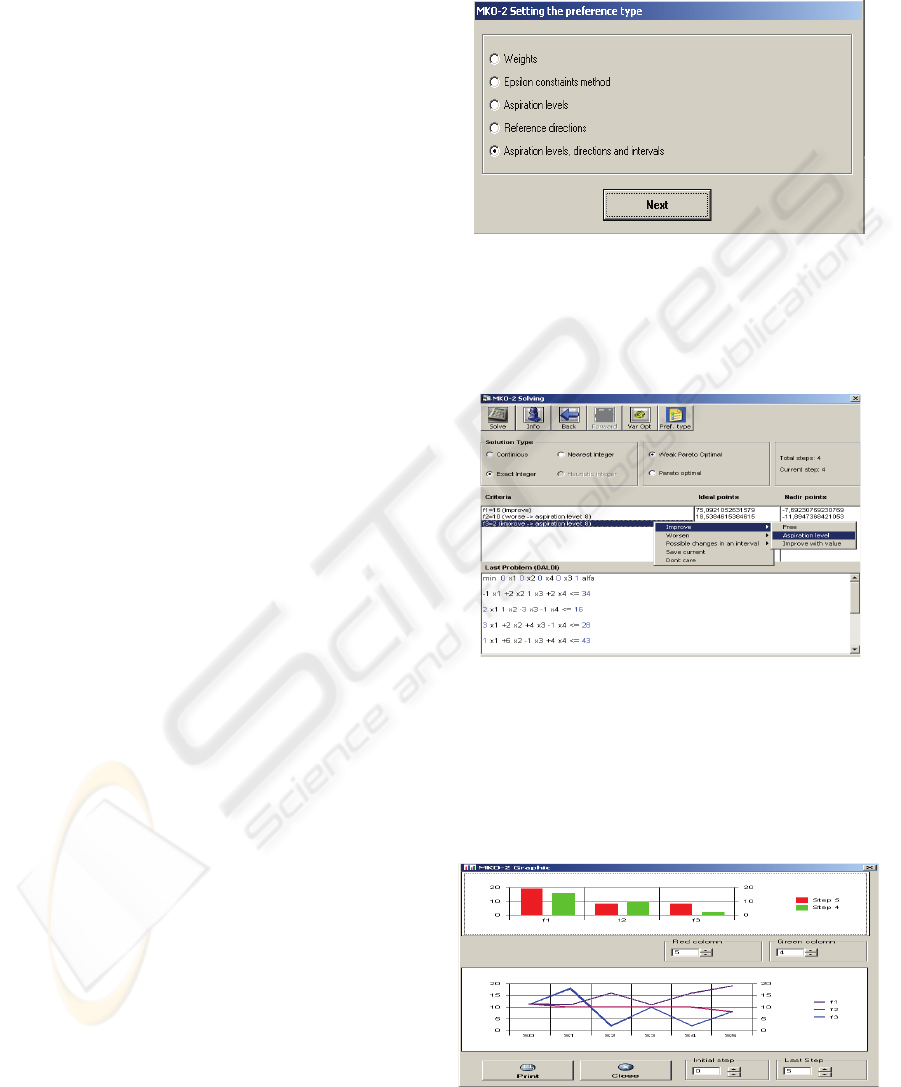
current and the final solutions. Figure 4, Figure 5

and Figure 6 show three of these windows. The

window in Figure 4 is designed to identify the type

of the DM’s preferences. The DM may select among

five types of preferences and let assume that he/she

has selected to set the preferences in the form of

desired and acceptable levels, directions and

intervals of alteration in the criteria values

(operating with DALDI scalarizing problem). The

screen in Figure 5 shows the setting of a new

aspiration level for the value of the third criterion.

Choosing “Graphic” command enables the

visualization of two types of graphical information

about the solving process. For this, a window with

with two types of graphics is opened (Figure 6).

Figure 4: Type of the DM’s Preferences.

With the help of the upper bar-graphic, it can be

made a visual comparison of the solutions found at

two iterations, selected in the fields for step

selection.

Figure 5: Setting of an aspiration level.

The lower graphic in Figure 6, can trace visually

the alteration of the values of the separate criteria at

different steps of the interactive process of searching

for a better solution. The initial and final steps of the

iteration interval can be defined, in which the values

of all the criteria are traced.

Figure 6: Two types of graphic.

ICEIS 2008 - International Conference on Enterprise Information Systems

280

4 CONCLUSIONS

The MultiOptima system is designed to support DM

in solving multicriteria analysis and multicriteria

optimization problems. The first part of the system –

the MKA-2 system, is designed to support the DM

in modelling and solving problems of multicriteria

ranking and multicriteria choice. The second part of

the system – the MKO-2 system, is designed to

model and solve linear and linear integer problems

of multicriteria optimization. The user-friendly

interface of the MKA-2 and MKO-2 systems

facilitates the operation of decision makers with

different qualification level relating to the

multicriteria analysis and multicriteria optimization

methods and software tools. The MKA-2 and MKO-

2 systems can be used both for education and for

real-life problems solving. The MultiOptima system

is a local multicriteria decision support system and

operates in two languages – Bulgarian and English.

A number of Bulgarian universities use the system

for education purposes, as well as for experimental

and research problems solving. A number of

governmental and private organizations and

companies use the system to solve real-life decision

making problems. The future development of the

MultiOptima system will be realized in two

directions. The first one is connected with the

implementing and adding of new methods for

multicriteria analysis and multicriteria optimization.

The second direction refers to developing of a web-

based version, enabling distant decision making.

ACKNOWLEDGEMENTS

This paper is partially supported by the National

Science Fund of Bulgarian Ministry of Education

and Science under the contract № I-1401\ 2004, and

by the Institute of Information Technologies - BAS

under the project № 010080 “Optimization methods

and systems” and the project № 010079 “Methods

and Tools for Processing Semantic Information”.

REFERENCES

Brans, J., Mareschal, B., 2005. PROMETHEE Methods.

In Multiple Criteria Decision Analysis: State of the Art

Surveys (J. Figueira, S. Greco and M. Ehrgott, Eds).

Springer Verlag, London, 163-196.

Coello C., Christiansen, A., 1999. MOSES: A

Multiobjective Optimization Tool for Engineering

Design. In Engineering Optimization, 31, 3, 337-368.

Deb, K., 2001. Multi-Objective Optimization Using Evo-

lutionary Algorithms, Wiley-Interscience Series in

Systems and Optimization, John Wiley & Sons.

Chichester.

Dyer, J., 2005. MAUT-Multiatribute Utility Theory. In

Multiple Criteria Decision Analysis: State of the Art

Surveys (J. Figueira, S. Greco and M. Ehrgott, Eds).

Springer Verlag, London, 265-297.

Ehrgott, M., Wiecek, M., 2005. Multiobjective

Programming. In Multiple Criteria Decision Analysis:

State of the Art Surveys (J. Figueira, S. Greco and M.

Ehrgott, Eds). Springer Verlag, London, 990-1018.

Figueira, J., Mousseau, V., Roy, B., 2005. ELECTRE

Methods. In Multiple Criteria Decision Analysis: State

of the Art Surveys (J. Figueira, S. Greco and M.

Ehrgott, Eds). Springer Verlag, London, 133-162.

Mladineo, N., Margeta, J., Brans, J. P., Mareshal, B.,

1987. Multicriteria Ranking of Alternative Locations

for Small Scale Hydroplants. In European Journal of

Operational Research, 31, 215-222.

Miettinen K., 2003. Interactive Nonlinear Multiobjective

Procedures. In Multiple Criteria Optimization: State of

The Art Annotated Bibliographic Surveys (M. Ehrgott

et al., Eds.). Springer, New York, 227-276.

Narula S., Vassilev, V., Genova, K., Vassileva, M., 2003.

A Partition-Based Interactive Method to Solve

Discrete Multicriteria Choice Problems. In

Cybernetics and Information Technologies, 2, 55-66.

Parsons, J., 2002. Agland Decision Tool: A Multicriteria

Decision Support System for Agricultural Property. In

Integrated Assessment and Decision Support, 3, 181-

187.

Paschetta, E., Tsoukiàs, A., 2000. A Real World MCDA

Application: Evaluating Software. In Journal of

Multiple Criteria Decision Analysis, 9, 205 – 226.

Rajesh, J. K., Gupta, S. K., Rangaih, G. P., Ray, A. K.,

2001. Multi-Objective Optimization of Industrial

Hydrogen Plants. In Chemical Engineering Science,

56, 999-1010.

Vanderbei, R., 1996. Linear Programming: Foundations

and Extensions, Kluwer Academic Publishers. Boston.

Vassileva, M., 2005. Generalized Scalarizing Problem Of

Multicriteria Optimization. In Comptes Rendus de

l’Academie Bulgare des Sciences, 58, 5, 537-544.

Vassileva M., Vassilev V., Staykov B., Dochev D., 2007.

Generalized Multicriteria Optimization Software

System MKO-2. In Procedeenigs of the 9th

International Conference ICEIS 2007, (G. Cordoso et

al., Eds.). Madeira, Portugal, 283-289.

Weistroffer, H., Smith, C., Narula, S., 2005. Multiple

Criteria Decision Support Software. In Multiple

Criteria Decision Analysis: State of the Art Surveys,

(J. Figueira, S. Greco and M. Ehrgott, Eds). Springer

Verlag, London, 990-1018.

Wolsey, L. A., 1998. Integer Programming, Wiley-

Interscience.

Zopounidis, C., Despotis, D. K., Kamaratou, I., 1998.

Portfolio Selection Using The AD

ELAIS

Multiobjective Linear Programming System. In

Computational Economics, 11, 189–204.

281

MULTICRITERIA DECISION SUPPORT SYSTEM MULTIOPTIMA