MACHINE GROUPING IN CELLULAR MANUFACTURING

SYSTEM USING TANDEM AUTOMATED GUIDED VEHICLE

WITH ACO BASED SIX SIGMA APPROACH

Iraj Mahdavi, Babak Shirazi and Mohammad Mahdi Paydar

Department of Industrial Engineering, Mazandaran University of Science & Technology, Babol, Iran

Keywords: Tandem automated guided vehicle; ant colony optimization; six sigma; intra and inter-loop flow.

Abstract: Effective design of material handling devices is one of the most important decisions in cellular manufacturing

system. Minimization of material handling operations could lead to optimization of overall operational costs.

An automated guided vehicle (AGV) is a driverless vehicle used for the transportation of materials within a

production plant partitioned into cells. The tandem layout is according to dividing workstations to some non-

overlapping closed zones that in each zone a tandem automated guided vehicle (TAGV) is allocated for

internal transfers. Also, among adjacent loops some places are determined for exchanging semi-produced parts.

This paper illustrates a non-linear multi-objective problem for minimizing the material flow intra and inter-

loops and minimization of maximum amount of inter cell flow, considering the limitation of TAGV work-

loading. For reducing variability of material flow and establishing balanced loop layout, some new constraints

have been added to the problem based on six sigma approach. Due to the complexity of the problem, ant

colony optimization (ACO) algorithm is used for solving this model. Finally this approach has been compared

with the existing methods to demonstrate the advantages of the proposed model.

1 INTRODUCTION

The design of automated material handling systems

is one of the most important decisions in facility

design activities for cellular manufacturing system

(CMS). An automated guided vehicle (AGV) is a

driverless vehicle used for the transportation of

goods and materials within a production plant

partitioned into cells, usually by following a wire

guide-path. One of the most important issues in

designing AGV systems is the guide-path design.

Material handling operations cover nearly 20–50%

of the overall operational costs (Kim and Tanchoco,

1991and Laporte et al., 1996). Tandem automated

guided vehicle (TAGV) was firstly proposed by

Bozer and Srinivasan (1991, 1992) that most of the

researches are being referred to them. They used two

principals of division and possession for AGV

systems. The base of tandem layout is according to

dividing work stations to some non-overlapping

closed zones that in each zone an AGV system is

allocated for internal transfers. Also, among adjacent

loops some places are determined for exchanging

produced parts, that numerous mutual exchanges are

possible in these places. Some of the advantages of

the TAGV systems that Bozer and Srinivasan (1991)

proposed may be the simplifying control in any loop

due to using one AGV in each zone, elimination of

intercurrent and traffic problems, determination of

optimum facility location for each work station,

effective support of group technology execution,

increasing the flexibility due to increase and

decrease of work stations by variation in production

design, and simplification of production operations

in each loop. The most significant problem in AGVs

is designing algorithms to determine the optimal

moving path.

A number of algorithms for AGV guide path

design have been developed over the past 20 years

(Sinriech and Tanchoco, 1993 and Farahani and

Tari, 2001).

The AGV guide-path configurations

discussed in previous research include Conventional

(Kaspi and Tanchoco, 1990; Kouvelis et al., 1992;

Seo and Egbelu et al., 1995; Kaspi et al., 2002; Ko

and Egbelu, 2003; Rajagopalan etal., 2004; Hillier

and Lieberman, 2005; nriech and Tanchoco, 1994;

Laporte et al., 2006) Tandem (Gaskin and Tanchoco,

1987; Gaskin et al., 1989; Chhajed et al., 1992;

Venkataramanan and WilsonNav, 1991; Farahani

and Tari, 2002) Single loop (Tanchoco and Sinriech,

1992; Banerjee and Zhou, 1995) bi-directional

shortest path (Kim and Tanchoco, 1991; Sun and

261

Mahdavi I., Shirazi B. and Mahdi Paydar M. (2008).

MACHINE GROUPING IN CELLULAR MANUFACTURING SYSTEM USING TANDEM AUTOMATED GUIDED VEHICLE WITH ACO BASED SIX

SIGMA APPROACH.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 261-267

DOI: 10.5220/0001697602610267

 SciTePress

Tchernev, 1996) and segmented flow (Sinriech et

al., 1994; Sinriech and Tanchoco, 1995; Sinriech

and Tanchoco, 1997; Barad and Sinriech, 1998). As

it is realized from the definition of tandem layout,

unlike the traditional layouts, is a hybrid system of

the mutual shortest path systems and one path loop

which is discussed in AGV system. Nonetheless,

the number of required TAGV in this system is

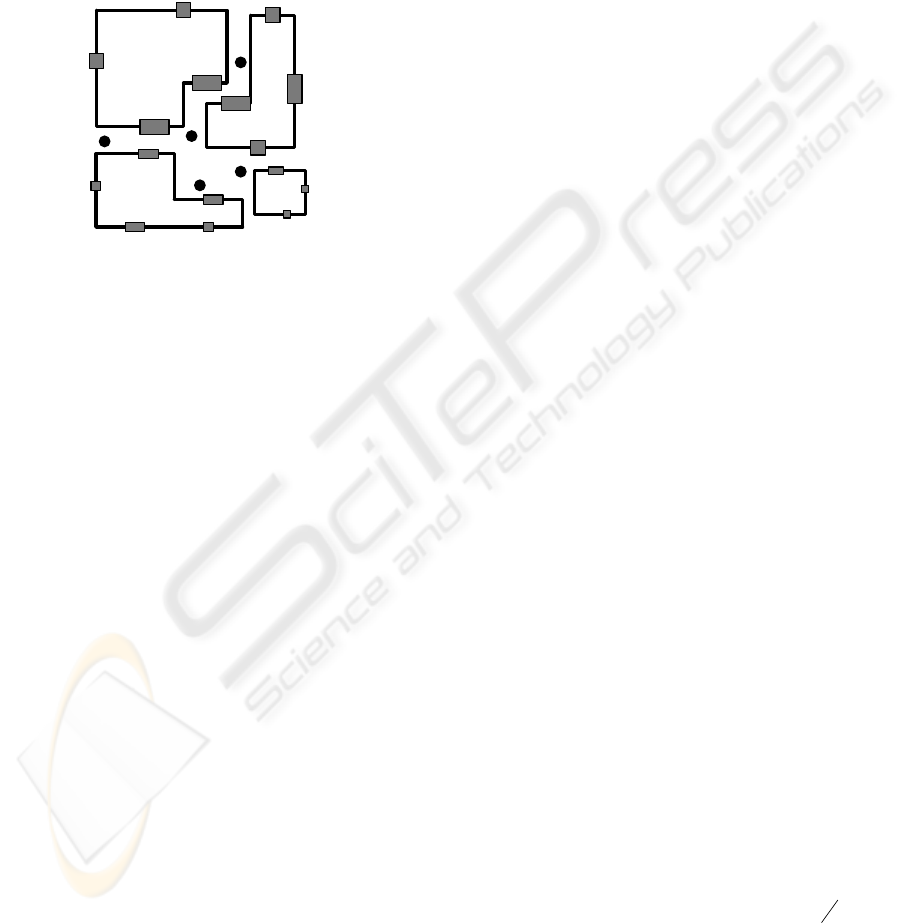
equal to the number of the loops as it is shown in

Figure 1.

Figure 1: Architecture of TAGV in cellular manufacturing.

In tandem systems different problems such as

machine partitioning, machine sequencing in each

loop, movement direction and pickup/deposit

(transfer) point determination are proposed in

literature (Gaskin and Tanchoco, 1987; Gaskin et al.,

1989; Banerjee and Zhou, 1995; Asef-Vaziri et al.,

2000; Asef-Vaziri et al., 2001; Farahani et al., 2005).

After Bozer and Srinivasan many researchers tried

on varied problems in tandem systems. One of the

most significant subjects in TAGV system is

partitioning machines to different zones. Machine

division in TAGV systems initially was proposed by

Bozer and Srinivasan with an analysis model. They

analyzed one AGV in one loop in that exploration.

They discussed a layout designation of a variable

path for AGV system and indicated that machine

partitioning in tandem AGV system have a direct

affect on the performance of the system. They

developed a heuristic division algorithm for AGV

system based on variable path in each zone and

identified the transfer location among zones during

that process by simulation.

This paper investigates the problem of machine

partitioning to specified number of loops (L). It

models a non-linear multi-objective problem for

minimizing the material flow intra and inter-loops and

minimization of maximum amount of inter cell flow,

considering the limitation of TAGV work-load. For

reducing variability of material flow and establishing

balanced loop layout some constraints add to problem

based on six sigma approach. Because of the

complexity of the problem ant colony optimization

(ACO) algorithm is used for solving this model. The

goal of proposed algorithm is to minimize problem

objectives along with the attainment of six sigma

compliance. Finally some test problems will be solved

by the ACO based designed program that is written

by using MATLAB 7 software, and compared

according to previous methods.

2 MATHEMATICAL MODEL

FOR MACHINE GROUPING TO

L PARTITIONS

In this section the objective is to identify machines

that should be allocated to each loop i.e. loops

formations are in a way that intra-loop and inter-

loop flow are minimum. The structure of machine

partitioning problem is similar to the structure of

CMS problems. The reason of using six sigma

constraints is to achieve a balanced flow with the

minimum fluctuations of inter-loop and intra-loop

flows.

Hence, the latter strategy is used to transform

the multi-objective function of the problem to a

single one because for problem optimization the

intra-loop and inter-loop flow are approximately

close to each other. In this paper a mathematical

model is represented that the objective is allocating

m machines to L loops in a way to close the flow

among varied loops rather than inter-loop flow

minimization and limitations satisfaction. Decision

variable and model parameters definitions are

coming next and then the mathematical model is

accompanied with its limitations.

2.1 Decision Variable

{

1 if machine is allocated to loop

0 otherwise

2.2 Parameters

m Machines predefined number

L Loops predefined number

i,k Machine counter i,k =1,2,..,m

,lj

Loop counter j = 1,2,..,L

Flow tolerance coefficient,

0.1

≤ p

Flow among machines i and k

(

)

Intra-loop flow for loop j

ICEIS 2008 - International Conference on Enterprise Information Systems

262

()

xΦ

Total inter-loop flow

T Total working time of TAGV in planning

period

Average time of load, unload, processing

of each part on machine i per unit time

Time of bottleneck in loop j

Upper bound of flow coefficient in each

loop,

=−

Upper bound of flow coefficient in

each loop,

Total flows from varied machines to

machine i,

iij

ϕϕ

=∀

∑

, C

Capability indices

The range of flow changes in each loop would

be small by choosing small

; therefore the flow in

loops will be closer to each other and vice versa by

taking large value of

.It is supposed that

varies

between 0.1 and

(

0.1

≤ p

). For the

Capability indices, If C

=2 and C

=1.5 the

probability of conformance can be shown to be

0.9999966. Thus C

>2 and C

>1.5 imply six sigma

logic.

2.3 Mathematical Model

The objective is to minimize inter-loop and intra-

loop flows based on cellular manufacturing systems

(CMS) and minimization of TAGV maximum

workload for minimizing the material flow costs.

According to the previous descriptions the following

model is represented:

()

in x x x

ik ij kj

ϕϕ

∑∑

, ik≠

(1)

()

1111

mLmL

in x x x

ik ij kl

ijkl

Φ=

====

∑∑∑∑

, ,ikjl≠≠

(2)

S.t.

1, 1, 2, ..., ,

xi m

∑

(3)

2, 1, 2,...,

≥=

∑

(4)

()

1111 11

mLmL mm

xxx

ik ij kl ik ij kl

ijkl ik

ϕϕϕ

≤

==== ==

∑∑∑∑ ∑∑

(5)

()

1111 11

mLmL mm

xxx

ik ij kl ik ij kl

ijkl ik

ϕϕϕ

≥

==== ==

∑∑∑∑ ∑∑

(6)

()tpx

jiiij

≥

(7)

()

txT

Bj ij

≤

∑

(8)

(1)

1111

mLmL

xmm ki

ij kl

ijkl

−≠

====

∑∑∑∑

(9)

xxx

ij kl ij kl

+≥

(10)

ik ik

ϕϕ

(11)

6( )

ik ik

ik ij kl

pk ik

ϕϕ

⎛⎞

−

⎜⎟

⎝⎠

∑∑

(12)

∑

(13)

ik ik

−

(14)

01{0,1}xx or

ij kl

=∈

(15)

Constraint (11) indicates that the flow is

confined within an interval. Equation (12) evaluates

the standard deviation for flow between machine i to

machine k. By incorporating C

in the evaluation of

standard deviation, the effect of loads and unloads

from the mean flow process has been taken into

account.

ik ik

− is the tolerance range of the flow i

to k . Equation (13) is used in evaluating the

standard deviation of the entire system. Equation

(14) helps in determining capability index C

check whether flow in system is six sigma compliant

or not. The objective of any tolerance synthesis

problem is to reduce the variation and obtain a

probability of non-conformance of at most 3.4 ppm.

This is guaranteed when the value of process

capability index of the entire CMS is higher (C

>=2

and C

>=1.5). Thus by taking C

=2 and C

=1.5 in

MACHINE GROUPING IN CELLULAR MANUFACTURING SYSTEM USING TANDEM AUTOMATED GUIDED

VEHICLE WITH ACO BASED SIX SIGMA APPROACH

263

calculating the value of σ

andσ

, it can be ensured

that each process in the CMS is six sigma compliant.

3 ANT COLONY OPTIMIZATION

BASED SIX SIGMA

CONSTRAINED ALGORITHM

Because of the time that these kinds of problems

occupy, meta-heuristic algorithms are used for solving

such problems. Ant colony optimization methods

have been successfully applied to diverse

combinatorial optimization problems including

traveling salesman, quadratic assignment, vehicle

routing. The ant systems emulate the behavior of real

ants. Ants deposit a substance called pheromone on

the path that they have traversed from the source to

the destination nest and the ants coming at a later

stage apply a probabilistic approach in selecting the

node with the highest pheromone trail on the paths.

Thus the ants move in an autocatalytic process

(positive feedback), favoring the path along which

more ants have traveled and by traverse all the nodes.

In the proposed ant System, ants are defined as simple

computational agents having some memory, they are

not completely ‘‘blind’’ like real ants and live in an

environment where time is discrete.

This paper presents an ant colony algorithm

with programming by MATLAB7. The structure of

the suggested algorithm is explained as follows:

4 INITIAL FEASIBLE SOLUTION

GENERATION BY K-MEANS

CLUSTERING (KMC) METHOD

One of the significant points for using all meta-

heuristic algorithms is generating initial feasible

solution for starting the optimization stages. In this

paper, for using ant algorithm, firstly the k-mean

model should be renovated. A k-means clustering

procedure is applied to generating initial solutions

(Laporte, 2006). By applying the KMC method to

clustering the m machines into L partitions, ensures

that no intersections will occur among the created

loops subject to 6 sigma constraints. On the other

hand, the workstations in a loop should be

reasonably close to each other, so that unnecessary

vehicle trips are avoided.

5 SOLVING THE PROBLEM

(ENCODING) (P ANTS

BETWEEN M MACHINE IN L

PARTITION)

For each ant p,let AL(p) be the set of nodes the p-th

ant allowed to meet at the next step. The selected p-

th ant node is added to the tabu list TL(p) for ant p.

For each ant, to be able to meet all m machines,

two information structure as AL(p) and TL(p) are

supposed, that TL(p) save the machines which are

met by each ant in time t and prohibit it to meet the

latter machine again before a complete tour. When a

tour of the algorithm is completed (m repetitions), to

compute the existing solution of each ant (P ants)

tabu list is used i.e. the flow that each ant passed all

machines is achieved by tabu list. Then the tabu list

is evacuated ant the ants are free to choose whatever

it wants. The flow amount of the p-th ant is reached

by TL(p) elements. TL

(p) is the s-th element of the

former list i.e. the s-th machine which is met by p-th

ant in the existing tour.

At the end, the sequence of the nodes visited by

the ant given by the tabu list specifies the solution

proposed by ant p. The node selection procedure is

purely probabilistic. Each ant selects the machine to

meet by the probability of remained pheromone trail

value function on the related arc between machines.

Let

)(t

be the intensity of the pheromone

trail between machine i and k on the edge (i,k) at the

time t. After choosing the next node, it will be time

(t+1). Therefore, if each ant similarly chooses its

next node, then all P ants (total number of ants) will

choose the next node to move in this interval, called

an iteration of the ACO algorithm, in time (t ,t+1)

After every m iterations, each ant has completed a

tour. At this point, the trail intensity is updated

according to the rule:

)(.)(

ikikik

tmt

Δ+

Where ρ is a coefficient that shows the trail

persistence between time t and t+

θ. In order to avoid

unlimited accumulation of the trail, the value of ρ

should lie in the range (0, 1). Also,

∑

Δ=Δ

ikik

ττ

Where P is the total number of ants and

is the quantity per unit time of the pheromone trail

laid on the edge (i,k) by p-th ant between times t and

t+ θ, and

ICEIS 2008 - International Conference on Enterprise Information Systems

264

⎪

⎭

⎪

⎬

⎫

⎪

⎩

⎪

⎨

⎧

+−

ℜ

=Δ

otherwise

tandttimebetweenkiedgetheonantthp

))(,(

Where

ℜ is a positive constant value which

denotes the remained ant's pheromone and

the amount of flow among machine i and k, by the p-

th ant. The transition probability of moving from

node i to node k for the given ant is as follows:

[()].[]

()

[()].[]

()

ik ik

if k AL p

ip ip

pALp

otherwise

αβ

τη

αβ

τη

⎧⎫

⎪⎪

∈

⎪⎪

⎨⎬

⎪⎪

∈

⎪⎪

⎩⎭

∑

Parameters α and β control the relative

importance of the trail versus the visibility in

which

means relative significance of pheromone

which is more than or equal to zero and

means

relative significance of visibility area which is more

than or equal to zero. The coefficient

means the

stability of pheromone

10 <

, (

−1

) could be

assumed as the amount of pheromone evaporation in

unit time.

Where AL(p) represents the set of nodes to

which ant p can move from the present state and

, the visibility from node i to node k (AL(p) = all

ants – TL(p)).

This information is called heuristic information

that is specific in any problem and is determined

regarding to the erudity of the programmer and

provides useful information from the beginning of

the problem to the ants. The value of it is constant

till the end of the problem.

After m repetitions all ants have completed one

tour and their tabu list is filled. Then the value of

is computed for each p-th ant and according to

equation --- the amount of

Δ is updated. Also

they found minimum flow by ants

(

min , 1,..., , 1,...,

Pandi k m

==) is saved and the

whole tabu lists are cleaned. This process is

continued till the completed tours counter which is

defined by the algorithm user, reach its maximum

value or all ants use a same completed tour.

5.1 Neighborhood Exchange Operator

The resulting clusters of ant-cycle algorithm could

be checked for six sigma constraints by comparing

to the level of cp & cpk,. In case of infeasibility ( in

6sigma), a simple search method is used by moving

some machines, following the defined neighborhood

evaluation method and based on the objective

function. The neighborhood of a solution is simply

obtained by removing a stochastic machine from

partition j and adding it to partition l, provided that it

does not create intersection (NEO (j,l)). Subjecting

to six sigma constraint, all

()

’s are computed

(j=1, 2,.., N),j-th partition is the partition with more

than two machines that has the most intra-loop flow,

and l-th partition is the one that has the least intra-

loop flow.

Step 1 – Initialize

Set t: =0; {t is the time of counter}

Generate initial feasible solutions by KCM.

Set NC: =0; {NC is the cycles counter}

For every edge (i,k) between machine i and

k , assign trial intensity

ikik

=:)( ;

0=Δ

;

Place the P ants on m machines (nodes)

Step 2 – Tabu list initialization

Set s: =1; {s is the tabu list index}

For p: =1 to P do

Place the starting machine

of the p-th ant in TL

(p);

Step 3- Ant movement on machines (this step

repeated m-1 times)

Repeat until tabu list is full

Set s: =s+1;

For p: =1 to P do

Choose the machine k

to move to, with probability

)(tp

;

{At the time t the p-

th ant is on machine i= TL

s-1

(p)}

Move the p-th ant to

the machine k;

Insert machine k to

(p);

End {For};

End {Repeat};

Step 4-

For p:=1 to P do

Move the p-th ant from TL

(p) to

(p);

Compute the

of the tour described

by p-th ant between machine i,k (for all P);

Update minimum flow among machine

i,k by finding min

;

MACHINE GROUPING IN CELLULAR MANUFACTURING SYSTEM USING TANDEM AUTOMATED GUIDED

VEHICLE WITH ACO BASED SIX SIGMA APPROACH

265

For every edge (i,k)

For p:=1 to P do

(, ) ( )

if i k tour described by TL p

otherwise

ℜ

⎧⎫

∈

⎪⎪

Δ=

⎨⎬

⎪⎪

⎩⎭

Δ= Δ

∑

;

Step 5-

For every edge(i,k) assign

ikikik

tmt

Δ+=+ )(.)(

;

Set t:=t+ m;

Set NC:=NC+1;

For every edge (i,k) set

Δ :=0;

Step6-

If (NC < NC

max

) & (stagnation

behavior)

then

Empty all tabu list;

Print all

(using

klij

xx ,

);

Compute

, C

;

If (C

<2) & (C

< 1.5)

then NEO(j,l);

Goto Step 2;

Else

Print minimum flow;

Step 7- Stop;

If the algorithm is stoped after NC repetitions,

the complexity order of ant-cycle algorithm is from

O(NC.m

.P). In reality in the first stage complexity

is from O(m

+ P) order, in the second stage it is

O(P), in the third stage it is O(m

.P), in the fourth

stage it is O(m

.P), in the fifth stage it is O(m

), and

in the sixth stage it is O(m.P).

6 COMPUTATIONAL

EXPERIMENTS

The proposed algorithm was coded in MATLAB.

The program was executed on the 5 test problem

using an IBM compatible PC with Pentium IV

processor and 1024MB of RAM. In all computations

examples are performed 10 times, based on six

sigma constraint ant cycle, by the designed software

and the best result is reported. Considering to the

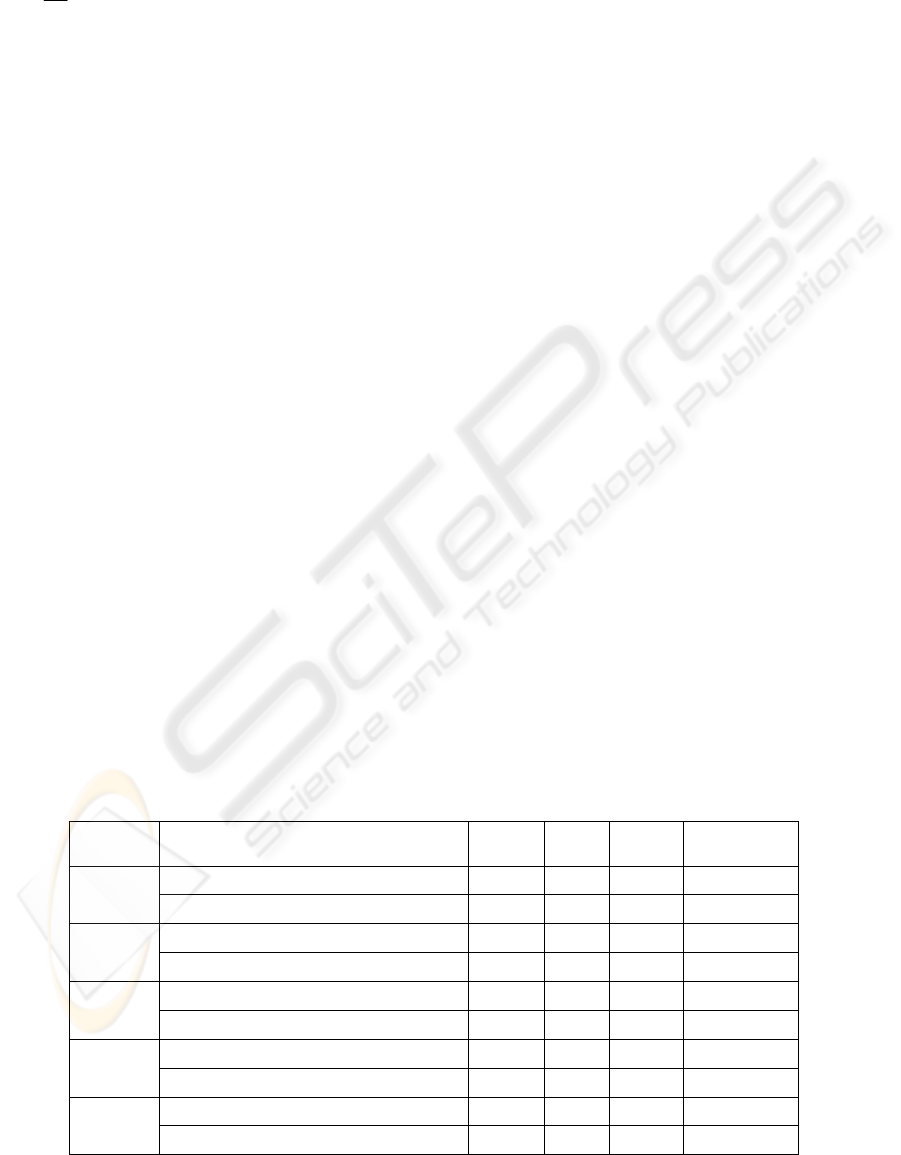
computational results that are presented in Table 1 it

is observed that the ant algorithm based designed

software most of the time find answers which are

equal to Lingo8 or better than it in less time. The

ACO parameters

ℜ

and

should be chosen

carefully as they might lead to poor performance of

the algorithm. Always the number of ants is equal to

the number of m machines. Varied values are tested

for a parameter while other parameters are fixed.

Almost 20 simulations are done to achieve a same

performance level with these parameters:

{1,100, 1000} , {0, 0.5,1 , 2 ,5} ,

{0, 1, 2, 5} , {0.3,0.5,0.7, 0.9,0.999}

βρ

ℜ

∈∈

The values of objective functions were

observed to select the best combination of these

values

100, 0.5, 1, 1

βα

ℜ

====

The combinations

( 1, 1), ( 1, 2),

βαβ

===

(1,5),(0.5,5)

βα β

===cause the same

performance level. The whole tests are done

for

max

10000NC

Table1: Comparing Six Sigma based with Lingo solutions.

Software

Time

(Sec)

(

)

xΦ

(

)

Decision variable

Iterative

Number

Lingo 7 1324 530

,,,,

11 21 32 42 52

xxxx

MATLAB 1.33 1324 530

,,,,

11 22 32 41 52

xxxx

Lingo 33 1523 544

,,,,,

12 21 31 41 52 62

xxxxx

MATLAB 1.85 1523 544

,,,,,

11 22 32 41 51 62

xxxxx

Lingo 207 1875 583

,,,,,,

12 22 31 41 52 61 72

xxxxxx

MATLAB 2.56 1793 583

,,,,,,

12 22 32 41 52 61 72

xxxxxx

Lingo 1568 2013 611

,,,,,,,

11 21 32 42 51 62 71 81

xxxxxxx

MATLAB 3.01 1983 598

,,,,,,,

11 21 32 41 51 62 71 81

xxxxxxx

Lingo 17658 2352 1452

,,,,,,,,

11 21 31 41 51 61 72 82 92

xxxxxxxx

MATLAB 3.02 2125 1261

,,,,,,,,

11 22 32 41 51 62 71 81 92

xxxxxxxx

ICEIS 2008 - International Conference on Enterprise Information Systems

266

7 CONCLUSIONS

In this paper by the means of six sigma strategy, a

non-linear mathematical model for machine

partitioning in TAGV systems is considered with

bi-objectives that are minimizing the material flow

intra & inter-loops and minimization of maximum

amount of inter cell flow. Regarding to the NP-hard

complexity of the problem, ant colony meta-

heuristic method is applied. Then in different test

problems the computational time and the objective

functions value of ant method is being compared

with traditional methods.

REFERENCES

Asef-Vaziri, A., Dessouky, M., Sriskandarajah, C., 2001.

A loop material flow system design for automated

guided vehicles. Int. J. Flex. Manuf. Sys. 13, 33–48.

Asef-Vaziri, A. Laporte, G. Sriskandarajah, C., 2005. The

block layout shortest loop design problem. IIE Trans.

32, 724–734.

Banerjee, P., Zhou, Y., 1995. Facilities layout design

optimization with single loop material flow path

configuration. Int. J. Prod. Res. 33, 183–203.

Barad, M., Sinriech, D., 1998. A Petri net model for the

operational design and analysis of segmented flow

topology (SFT) AGV system. Int. J. Prod. Res. 36,

1401–1426.

Bozer, Y.A., Srinivasan, M.M., 1991. Tandem

configuration for automated guided vehicle systems

and the analysis of single vehicle loops. IIE Trans. 23,

72–82.

Bozer, Y.A., Srinivasan, M.M., 1992. Tandem AGV

systems: a partitioning algorithm and performance

comparison with conventional AGV systems. Eur. J.

Operat. Res. 63, 173–191.

Chhajed, D., Montreuil, B., Lowe, T., 1992.Flow network

design for manufacturing systems layout. Eur. J.

Operat. Res. 57 - 145–161.

Farahani, R.Z., Tari, F.G., 2001. Optimal flow path

designing of unidirectional AGV systems. Int. J. Eng.

Sci. 12 , 31–44.

Farahani, R.Z., Tari, F.G., 2002. A branch and bound

method for finding flow-path designing of AGV

systems. IIE Trans. 15 , 81–90.

Farahani, R.Z., Laporte, G., Sharifyazdi, M., 2005 A

practical exact algorithm for the shortest loop design

problem in a block layout. Int. J.Prod. Res. 43, 1879–

1887.

Gaskin, R.J., Tanchoco, J.M.A., 1987. Flow path design

for automated guided vehicle system. Int. J. Prod. Res.

25, 667–676.

Gaskin, R.J., Tanchoco, J.M.A., Taghaboni, F., 1989.

Virtual flow paths for free ranging automated guided

vehicle systems. Int. J. Prod. Res. 27, 91–100.

Hillier, F.S., Lieberman, G.J., 2005. McGraw-Hill

International Edition, Eight edition. Operations

Research.

Kaspi, M., Tanchoco, J.M.A., 1990. Optimal flow path

design of unidirectional AGV systems. Int. J. Prod.

Res. 28, 1023–1030.

Kaspi, M., Kesselman, U., Tanchoco, J.M.A., 2002.

Optimal solution for the flow path design problem of a

balanced unidirectional AGV system, Int. J. Prod.

Res. 40, 349–401.

Kim, C.W.. Tanchoco, J.M.A., 1991. Conflict-free

shortest-time bi-directional AGV routing. Int. J. Prod.

Res. 29, 2377–2391.

Ko, K.C., Egbelu, P.J., 2003. Unidirectional AGV guide

path network design: a heuristic algorithm. Int. J.

Prod. Res. 41, 2325–2343.

Kouvelis, P., Gutierrez, G.J., Chiang, W.C., 1992.

Heuristic unidirectional flow path design approach for

automated guided vehicle systems. Int. J. Prod. Res.

30, 1327–1351.

Laporte, G., Asef-Vaziri, A., Sriskandarajah, C., 1996.

Some application of the generalized traveling

salesman problem. J. Oper. Res. Soc. 47,1461–1467.

Laporte, G., Farahani, Z.R., 2006. Elnaz Miandoabchi,

Designing an efficient method for tandem AGV

network design problem using tabu search. Applied

Mathematics and Computation.

Lin, J.T., Chang, C.C.K., Liu, W.C., 1194. A load routing

problem in a tandem-configuration automated guided

vehicle system, Int. J. Prod.Res. 32, 411–427.

Rajagopalan, S., Heragu, S.S., Taylor G.D., 2004. A

Lagrangian relaxation approach to solving the

integrated pick-up/drop-off point and AGV flow path

design problem. Appl. Math. Model. 28, 735–750.

Seo, Y., Egbelu, P.J., 1995. Flexible guide path design for

automated guided vehicle systems. Int. J. Prod. Res.

33, 1135–1156.

Sinriech, D., Tanchoco, J.M.A., 1991. Intersection graph

method for AGV flow path design, Int. J. Prod. Res.

29, 1725–1732.

Sinriech, D., Tanchoco, J.M.A., 1993. Solution methods

for the mathematical models of single loop AGV

systems. Int. J. Prod. Res. 31, 705–726.

Sinriech, D., Tanchoco, J.M.A., 1994. SFT – segmented

flow topology, in: J.M.A. Tanchoco (Ed.), Material

Flow System in Manufacturing, Chapter 8. Chapman

and Hall, London, 200–235.

Sinriech, D., Tanchoco, J.M.A., 1995. An introduction to

the segmented flow approach to discrete material flow

systems. Int. J. Prod. Res. 33, 3381–3410.

Sinriech, D., Tanchoco J.M.A., 1997. Design procedures

and implementation of the segmented flow topology

(SFT) for discrete material flow systems. IIE Trans.

29, 323–335.

Sun, X.-C., Tchernev, N., 1996. Impact of empty vehicle

flow on optimal flow path design for unidirectional

AGV systems. Int. J. Prod. Res. 34, 2827–2852.

Tanchoco, J.M.A., Sinriech, D., 1992. OSL – optimal

single loop guide paths for AGVs. Int. J. Prod. Res.

30, 665–681.

Venkataramanan, M.A., Wilson, K.A., 1991. A branch-

and bound algorithm for flow path design of

automated guided vehicle systems. Nav. Res. Logist.

Q. 38, 431–445.

MACHINE GROUPING IN CELLULAR MANUFACTURING SYSTEM USING TANDEM AUTOMATED GUIDED

VEHICLE WITH ACO BASED SIX SIGMA APPROACH

267