ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN

SIMILARITY-BASED DIAGNOSIS OF ACTIVE SYSTEMS

Gianfranco Lamperti, Federica Vivenzi and Marina Zanella

Dipartimento di Elettronica per l’Automazione, Via Branze 38, 25123 Brescia, Italy

Keywords:

Similarity-based diagnosis, discrete-event systems, temporal observations, subsumption.

Abstract:

Similarity-based diagnosis of large active systems is supported by reuse of knowledge generated for solving

previous diagnostic problems. Such knowledge is cumulatively stored in a knowledge-base, when the diag-

nostic session is over. When a new diagnostic problem is to be faced, the knowledge-base is queried in order

to possibly ﬁnd a similar, reusable problem. Checking problem-similarity requires, among other constraints,

that the observation relevant to the new problem be subsumed by the observation relevant to the problem in

the knowledge-base. However, checking observation-subsumption, following its formal deﬁnition, is time and

space consuming. The bottleneck lies in the generation of a nondeterministic automaton, its subsequent trans-

formation into a deterministic one (the index space of the observation), and a regular-language containment-

checking. In order to speed up the diagnostic process, an alternative technique is proposed, based on the

notion of coverage. Besides being effective, subsumption-checking via coverage is also efﬁcient because no

index-space generation or comparison is required. Experimental evidence supports this claim.

1 INTRODUCTION

Discrete-event systems (DESs) (Cassandras and

Lafortune, 1999) are dynamic systems, typically

modeled as networks of components. Each com-

ponent is a communicating automaton (Brand and

Zaﬁropulo, 1983) that reacts to input events by state-

transitions which possibly generate new events to-

wards other components. Diagnosis of DESs is a

challenging task that has been tackled since a decade

via different approaches, either based on artiﬁcial in-

telligence (Pencol´e, 2000; Roz´e and Cordier, 2002;

Console et al., 2002; Pencol´e and Cordier, 2005) or

automatic control techniques (Sampath et al., 1995;

Sampath et al., 1996; Chen and Provan, 1997; Sam-

path et al., 1998; Zad et al., 1999; Cassandras and

Lafortune, 1999; Lunze, 2000; Debouk et al., 2000;

Schullerus and Krebs, 2001). Within the domain of

a class of asynchronous DESs (Baroni et al., 1999;

Lamperti and Zanella, 2003; Lamperti and Zanella,

2004; Lamperti and Zanella, 2006b), called active

systems, a diagnosis approach has been proposed

that is based on similarity techniques (Lamperti and

Zanella, 2006a; Cerutti et al., 2007) with the aim of

pursuing reuse of knowledge when solving a diagnos-

tic problem. The idea is to store into a knowledge-

base the data structures generated for solving each di-

agnostic problem. When a new problem is to be faced,

instead of solving it from scratch, the knowledge-base

is ﬁrst browsed in order to ﬁnd a previously-solved

diagnostic problem that is ‘compatible’ with the new

one. If so, the knowledge relevant to the old problem

can be exploited to solve the new problem, thereby

speeding up the diagnostic process. Among other

constraints, such compatibility requires that the obser-

vation relevant to the problem in the knowledge-base

subsume the observation relevant to the new prob-

lem. Such an observation is temporal in nature, and

is represented by a DAG. The problem lies on the

mode in which subsumption is checked, which, ac-

cording to the deﬁnition of subsumption, is based on

a containment relationship between the regular lan-

guages of the index spaces of the observations. The

index space is a deterministic automaton whose gen-

eration (and comparison) may require considerable

computational resources. So, this paper proposes

an alternative, more efﬁcient, approach for checking

observation-subsumptionthat avoids index-space ma-

nipulation, by reasoning on the speciﬁc properties of

the observations.

Lamperti G., Vivenzi F. and Zanella M. (2008).

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE SYSTEMS.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 44-53

DOI: 10.5220/0001696200440053

 SciTePress

2 BACKGROUND

When an active system reacts, it generates a sequence

of observable labels, called the signature of the reac-

tion. However, what is actually perceived by the ex-

ternal observer is a relaxation of the signature S. Such

a relaxation is called a temporal observation. For-

mally, let L be the ﬁnite domain of all the observable

labels the active system can generate, possibly includ-

ing the null label ε. A temporal observation is a (not

necessarily connected) DAG

O = (N ,L ,A ) (1)

where N is the set of nodes, with each N ∈ N being

marked with a non-empty subset of L , and A : N 7→

is the set of arcs. A ‘≺’ temporal precedence re-

lationship among nodes of the graph is deﬁned as fol-

lows:

• If N 7→ N

′

∈ A then N ≺ N

′

;

• If N ≺ N

′

and N

′

≺ N

′′

then N ≺ N

′′

;

• If N 7→ N

′

∈ A then ∄N

′′

∈ N (N ≺ N

′′

≺ N

′

The set of labels marking a node N is the extension of

N, written kNk. Thus, the relaxation of the signature

S into O involves three kinds of uncertainty:

• Logical uncertainty: each single observable label

in the signature S is instead perceived as a set of

candidate labels, possibly including the null label

ε. All labels in kNk but one are spurious, with just

one being the actual label.

• Temporal uncertainty: the absolute temporal or-

dering of the signature S is relaxed to partial tem-

poral ordering. If N ≺ N

′

in O , where ℓ and ℓ

′

are

the actual labels in N and N

′

, respectively, then

ℓ precedes ℓ

′

in S. However, not all precedence

relationships between nodes in N are known.

• Node uncertainty: additional spurious nodes that

involve ε (among other labels), are possibly in-

serted

As such, O implicitly incorporates several candidate

signatures, where each candidate is determined by se-

lecting one label from each node in N without vio-

lating the temporal constraints imposed by the prece-

dence relationships. The set of all the candidate sig-

natures of O is called the extension of O , written kO k.

Among such candidates is the actual signature S. Like

for nodes, all candidate signatures but one are spu-

rious. The mode in which the signature S demeans

If the actual label is ε, it means that no label was actu-

ally generated by the system. Note how the extension of a

node in N cannot be the singleton {ε}.

In a spurious node, the actual label is ε, with all the

other labels being spurious.

Figure 1: Observations O

(left) and O

(right).

to observation O is assumed to be unknown.

explained i,n (Lamperti and Zanella, 2002), such a

degradation may be caused by the multiplicity of the

communication channels that convey observable la-

bels from the system to the observer (temporal un-

certainty), and to noise (logical uncertainty). How-

ever, although unknown, S is assumed to be preserved

within O .

Example 1. Shown in Fig. 1 are the graphs of two

(both logically and temporally uncertain) observa-

tions, namely, from left to right, O

= (N

)

and O

= (N

), where N

= {N

,...,N

}, N

= {N

′

,...,N

′

}, L

= {a,b,c, d, f,ε}, and L

= {a,b,

c,d,ε}. In O

, N

′

incorporates the ﬁrst observable la-

bel, namely a. Then, either N

′

or N

′

follows, each

of which involves two candidate labels, where ε is the

null label. The last generated node is N

′

, with a and

ε being the ﬁnal candidate labels. The extension of

the observation, namely kO

k, includes the candidate

signatures ac, ad, abc, abd, aca, ada, acb, adb, abca,

abda, acba, adba, each of which is obtained by se-

lecting one label for each node without violating the

temporal constraints, where the null label ε has been

removed.

Within the diagnostic process it is inconvenient

to reason on the observation O as is, mostly be-

cause the explanation-oriented diagnostic reasoning

requires some sort of observation-indexing. Such

an indexing is more naturally performed based on a

surrogate of the observation, called the index space,

namely Isp(O ). This is a deterministic automaton

with the property that its regular language is the ex-

tension of O ,

Lang(Isp(O )) = kO k. (2)

In other words, the set of strings generated by each

path in Isp(O ), from the initial state to a ﬁnal state,

equals the set of candidate signatures relevant to O .

As detailed in (Cerutti et al., 2007), the generation of

the index space of O requires two steps, namely:

• Yielding the nondeterministic automaton, called

the preﬁx space of O , where each node identiﬁes

the set of consumed nodes in N up to now;

Otherwise, in principle, we might distill S from O ,

thereby disregarding O in the diagnostic process.

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE

SYSTEMS

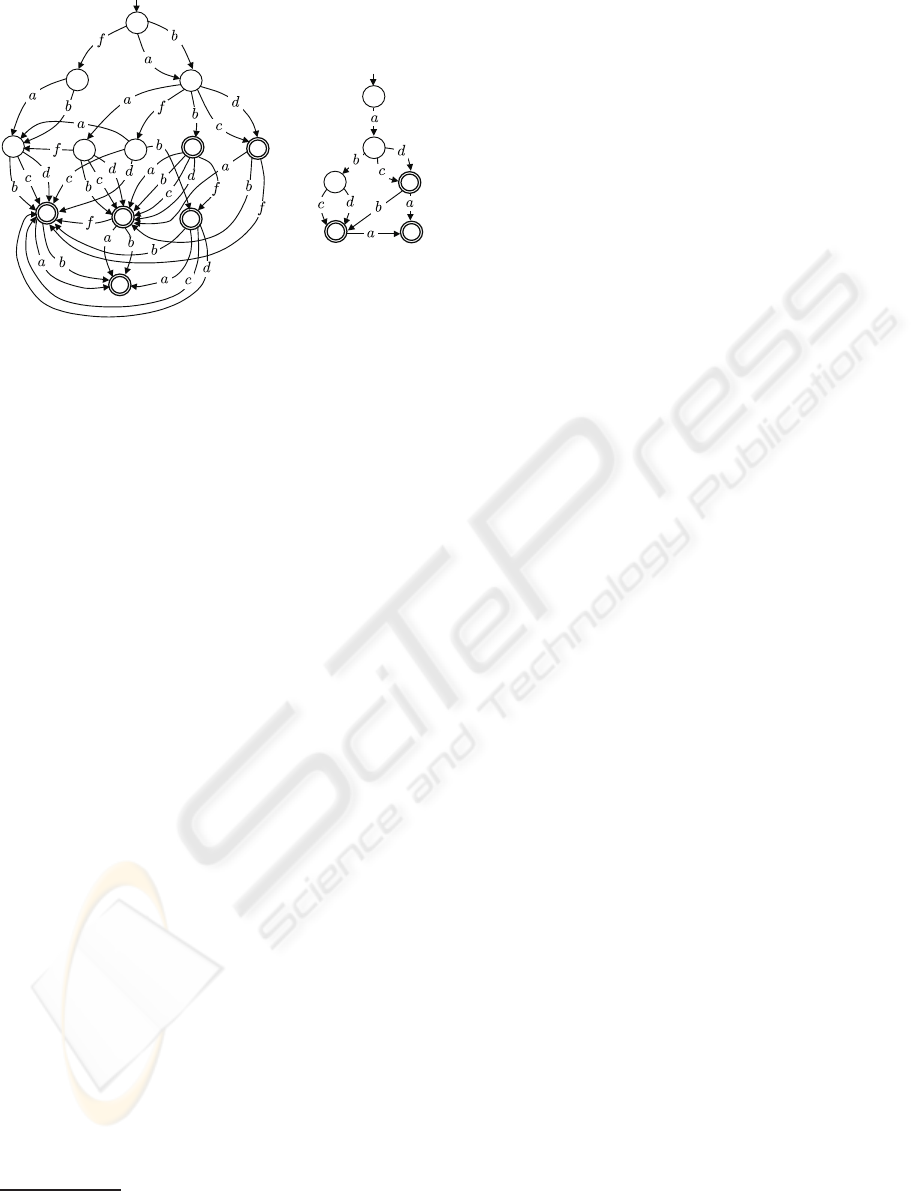
Figure 2: Index spaces Isp(O

) (left) and Isp(O

) (right) .

• Generating the deterministic automaton equiva-

lent to the preﬁx space, in fact the index space.

Furthermore, as explained shortly, the role of the in-

dex space comes into view for checking observation-

subsumption too.

Example 2. Shown in Fig. 2 are the index spaces

of observations O

(left) and O

(right) displayed in

Fig. 1. It is easy to check that the regular language of

each index space equals the extension of the relevant

observation (the set of candidate signatures), where

each string of the language corresponds to a path in

the index space, from the initial state to one of the ﬁ-

nal states (with the latter being double circled in the

ﬁgure). In particular, Example 1 offers evidence that

Lang(Isp(O

)) = kO

In similarity-based diagnosis of DESs (Lamperti

and Zanella, 2006a), it is essential to understand

whether the solution of the diagnostic problem ℘

′

at hand can be supported by the knowledge yielded

for solving a previous (different) diagnostic problem

℘, with the latter being stored in a knowledge-base.

Among other constraints, reuse of℘can be exploited

only if the observations O

′

and O relevant to ℘

′

and

℘, respectively, are linked by a subsumption relation-

ship,

O ⋑ O

′

(3)

namely, only if O subsumes O

′

. The subsumption re-

lationship is deﬁned in terms of regular-languagecon-

tainment, relevant to the corresponding index spaces,

precisely:

Lang(Isp(O )) ⊇ Lang(Isp(O

′

)). (4)

Being equivalent, both the preﬁx space and the index

space share the same regular language (Hopcroft et al.,

2006).

This means that O subsumes O

′

iff the set of candidate

signatures of O includes all the candidate signatures

of O

′

The reason why observation subsumption sup-

ports reuse can be roughly explained as follows. The

solution of ℘ yields an automaton µ, a sort of diag-

noser, where each state is marked by a set of diag-

noses and each transition is marked by a label in L .

The language of µ is the subset of the signatures rel-

evant to O that comply with the model of the system,

namely, Lang(µ) ⊆ kO k. The same applies to a new

problem ℘

′

relevant to O

′

. However, if O ⋑ O

′

, that

is, kO k ⊇ kO

′

k, then Lang(µ) ⊇ Lang(µ

′

). In other

words, µ contains all the signatures of µ

′

. This allows

the diagnostic engine to reuse µ in order to generate

′

based on O

′

. The advantage stems from the fact

that such an operation is far more efﬁcient than gen-

erating µ

′

from scratch, which would require heavy

model-based reasoning.

Example 3. With reference to observations O

and

outlined in Fig. 1, and the relevant index spaces in

Fig. 2, it is easy to check that O

⋑ O

, that is, kO

k ⊇

k. In other words, each string in Lang(Isp(O

)) is

also a string in Lang(Isp(O

)).

The problem with observation-subsumption

checking lies on the fact that, establishing whether

we can exploit the knowledge for solving ℘, in

order to solve ℘

′

, requires a considerable amount

of computational resources. Speciﬁcally, we need

ﬁrst generate Isp(O

′

) and, subsequently, compare

Lang(Isp(O

′

)) with each Lang(Isp(O )) in the

knowledge-base, in the hope of ﬁnding a subsuming

observation O . Such an approach, based on the gen-

eration of the index space and on regular-language

containment-checking, may be prohibitive in real

applications. In order to cope with this complexity,

we need some alternative checking-techniques.

3 CHECKING SUBSUMPTION

The systematic nature of checking based on the for-

mal deﬁnition of subsumption stems primarily on its

lack of prospection (short-sightedness). As a mat-

ter of fact, such a systematic technique does not per-

form any kind of reasoning on the given observations.

Assume the problem of testing O ⋑ O

′

, namely the

checking problem. The idea is to ﬁnd out some condi-

tions that either imply or are implied by such a re-

lationship. If these conditions can be checked us-

ing a reasonable amount of computational (space and

time) resources, then chances are that we can give an

answer to the checking problem efﬁciently. Specif-

ically, if a necessary condition N

is violated, then

ICEIS 2008 - International Conference on Enterprise Information Systems

the answer to the checking problem will be no. Du-

ally, if a sufﬁcient condition S

holds, then the an-

swer will be yes. However, if either N

holds or S

is violated, then the checking problem remains unan-

swered. Necessary conditions and sufﬁcient condi-

tions relevant to the checking problem are given in

Theorem 1 and Theorem 2, respectively. As shown

shortly, these conditions are eventually incorporated

within Algorithm 1 (see below).

Theorem 1. Let O = (N ,L , A ) and O

′

) be two temporal observations. Let

n and n

′

be the number of nodes in N and N

′

respectively. Let n

and n

′

be the number of nodes

that include the null label ε in N and N

′

, respec-

tively. Let M and M

′

be the multisets of observable

labels occurring in O and O

′

, respectively. Then, O

subsumes O

′

only if the following conditions hold:

n ≥ n

′

(5)

− n

′

≥ n− n

′

(6)

M ⊇ M

′

. (7)

Proof. The proof is by contradiction. To prove con-

dition (5), we have to show that O ⋑ O

′

⇒ n ≥ n

′

Assume the contrary, namely n

′

> n. Since ∀N

′

∈

′

(kN

′

k 6= {ε}), we can make up a temporal se-

quence T by selecting a label ℓ 6= ε for each N

′

∈ N

′

where |T| = n

′

. Clearly, T /∈ kIsp(O )k because tem-

poral sequences relevant to O are long at most n.

Hence, kIsp(O )k 6⊇ kIsp(O

′

)k, that is, O 6⋑ O

′

, a con-

tradiction.

To prove condition (6), we have to show that O ⋑

′

⇒ n

− n

′

≥ n − n

′

. Assume the contrary, namely

n− n

′

> n

− n

′

or, in other terms,

n− n

> n

′

− n

′

. (8)

Let N

′

= {N

′

| N

′

∈ N

′

,ε ∈ kN

′

k}. Now, consider a

sequence L

′

of labels selected from all nodes of N

′

in such a way that ε is chosen for all nodes in N

′

Let T

′

be the temporal sequence corresponding to L

′

Clearly, |T

′

| = n

′

−n

′

. In consequence, T

′

/∈ kIsp(O )k

because each temporal sequence T relevant to O is

such that |T| ≥ n− n

, that is, based on equation (8),

|T| > n

′

− n

′

, hence, |T| > |T

′

|. Thus, kIsp(O )k 6⊇

kIsp(O

′

)k, that is, O 6⋑ O

′

, a contradiction.

To prove condition (7), we have to show that

O ⋑ O

′

⇒ M ⊇ M

′

. Assume the contrary, namely

M 6⊇ M

′

, that is, M

′

⊃ M . This means that M

′

will

contain k

′

≥ 1 occurrences of a label ℓ, with M in-

cluding k ≥ 0 occurrences of the same label, where

′

> k. Choose L

′

so as to include all k

′

occurrences

of ℓ in O

′

. Hence, T

′

will contain exactly k

′

occur-

rences of ℓ. On the other hand, no temporal sequence

L can be composed in O to include the same number

of occurrences of ℓ. Thus, kIsp(O )k 6⊇ kIsp(O

′

)k, that

is, O 6⋑ O

′

, a contradiction. 

Corollary 1.1. O subsumes O

′

only if

L ⊇ L

′

. (9)

Proof. Condition (9) is entailed by condition (7) of

Theorem 1, with the latter being necessary for O ⋑

′

to hold. Hence, condition (9) too is a necessary

condition for observation subsumption. 

Example 4. In Example 3 we have shown that O

subsumes O

, where such observations are displayed

in Fig. 1. Hence, the conditions relevant to The-

orem 1 are expected to hold for O

and O

. We

have n

= 5, n

= 4, n

= 3, n

= 2. As a mat-

ter of fact, both conditions (5) and (6) hold. More-

over, since M

= [a,a, a,b,b,b,b, c, d, f,ε,ε,ε] and

= [a,a,b,c, d,ε,ε], condition (7) holds too.

The conditions necessary for subsumption stated

in Theorem 1 can be easily checked. Thus, they cor-

respond to the ﬁrst actions of the checking algorithm.

If one of them is violated, the check terminates im-

mediately with a negative answer. Otherwise, the

check continues by testing a sufﬁcient condition of

subsumption based on the notion of coverage given

in Deﬁnition 1 below. Roughly, O covers O

′

when O

is a relaxation of O

′

, inasmuch as an observation is a

relaxation of a system signature.

Deﬁnition 1. (Coverage) Let O = (N , L , A ) and

′

= (N

′

) be two temporal observations,

where N = {N

,...,N

} and N

′

= {N

′

,...,N

′

}. We

say that O covers O

′

, written O D O

′

, iff there ex-

ists a subset

N of N , with

N = {

,...,

′

} hav-

ing the same cardinality as N

′

, such that, denoting



N −



, we have:

(1) (ε-coverage): ∀N ∈ N

(ε ∈ kNk);

(2) (logical coverage): ∀i ∈ [1..n

′

] (k

k ⊇ kN

′

k);

(3) (temporal coverage): For each path

,...,N

i in O , where

∈

N ,

∈

N ,

s ≥ 0, ∀k ∈ [1.. s]



∈ N



, the following holds

in O

′

: N

′

≺ N

′

Example 5. With reference to the observations dis-

played in Fig. 1, it is easy to show that O

D O

. As-

sume the subset of N

being

= {N

Hence, N

= {N

}. Clearly, ε-coverage holds, as ε ∈

k. Logical coverage holds too, as kN

k ⊇ kN

′

k ⊇ kN

′

k, kN

k ⊇ kN

′

k, and kN

k ⊇ kN

′

k. It

is easy to check that temporal coverage occurs. For

instance, for hN

i, where N

∈ N

, we have

′

≺ N

′

in O

Theorem 2 and Note 1 offer evidence that cover-

age is only sufﬁcient for subsumption, not necessary.

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE

SYSTEMS

However, in practice, if coverage does not hold, it is

unlikely for subsumption to hold. Note that, since

coverage entails subsumption, the conditions in The-

orem 1 are necessary for coverage too.

Theorem 2. Coverage entails subsumption:

O D O

′

=⇒ O ⋑ O

′

. (10)

Proof. The proof is based on Deﬁnition 1 and Deﬁ-

nition 2 (the latter given below).

Deﬁnition 2. (Sterile sequence) Let

N =

,...,

′

i be an ordering

of nodes in

N .

The sterile sequence of

N ,



,...,N

′



(11)

is a sequence of subsets of N

, called sterile sets, in-

ductively deﬁned as follows:

• (Basis) N

is deﬁned by the following two rules:

(1) If N ∈ N

, N is a root of O , then N ∈ N

(2) If N ∈ N

, all parents of N are in N

, then

N ∈ N

;

• (Induction) Given N

, i ∈ [0..(n

′

− 1)], the suc-

cessive sterile set N

i+1

is deﬁned by the following

two rules:

(3) If N ∈ N

, all parents of N are in



∗

∪



i+1



, then N ∈ N

i+1

(4) If N ∈ N

, all parents of N are in



∗

∪



i+1



∪ N

i+1



, then N ∈ N

i+1

where N

∗

, i ∈ [0.. n

′

], is recursively deﬁned as fol-

lows:

∗



if i = 0

∗

i−1

∪





∪ N

otherwise.

(12)

To prove the theorem, it sufﬁces to show that each

candidate signature S in the index space of O

′

is also

a candidate signature in the index space of O , namely:

∀S ∈ kIsp(O

′

)k (S ∈ kIsp(O )k ). (13)

According to Theorem 1 in (Lamperti and Zanella,

2002), S is the sequence of labels obtained by select-

ing, without violating the precedence constraints of

′

, one label from each node in N

′

, and by removing

all the null labels ε. Let

′

= h

′

,...,

′

i (14)

be the ordering of N

′

relevant to the choices of such

labels. Accordingly, the sequence L

′

of the chosen

labels can be written as

′

= hℓ | ℓ ∈ k

′

k,i ∈ [1..n

′

]i (15)

An ordering of a set is asequence involving all and only

the elements in the set, without duplicates.

while the candidate signature S is in fact

S = hℓ | ℓ ∈ L

′

,ℓ 6= εi. (16)

We need to show that there exists an ordering N of

N fulﬁlling the precedence constraints imposed by

A , from which it is possible to select a sequence L of

labels,

L = hℓ

,ℓ

,...,ℓ

i (17)

such that the subsequence of non-null labels in L

equals S:

hℓ | ℓ ∈ L,ℓ 6= εi = S. (18)

Note how N (as well as any other ordering of N ) can

be represented as a sequence of nodes in

N , with each

node being interspersed with (possibly empty) subse-

quences N

of nodes in N

, speciﬁcally

N = N

∪ h

i ∪ N

∪ h

i ∪ N

...h

′

i ∪ N

′

(19)

where

′

[

i=1

{

} =

N ,

′

[

i=0

= N

′

i=0

0. (20)

The proof is by induction on L

′

. Let L

′

denote the

subsequence of L

′

up to the i-th label, i ∈ [1..n

′

Let L

denote the subsequence of L relevant to the

choices of labels performed in correspondence of

the labels in L

′

. Let S

and S

′

denote the candidate

signatures corresponding to L

and L

′

, respectively.

(Basis) No label is chosen in O

′

, that is, L

′

= hi. We

choose a sequence of empty labels for all the nodes

in N

, which is clearly possible according to the

property that N

is a sterile set composed of nodes

having ancestors in N

only. In other words, N

an ordering of N

, while L

= hε,ε,... ,εi, hence,

= S

′

= hi.

(Induction) We assume that L

and L

′

i ∈ [0..(n

′

− 1)], are such that S

= S

′

. We also as-

sume that, given the sequence h

′

,...,

′

i of chosen

nodes in O

′

, the corresponding sequence of chosen

nodes in O is N

∪h

i∪ N

∪h

i∪ N

...h

i∪ N

where, ∀k ∈ [1..i], if

′

is the node N

′

in N

′

, then

is the node

N , and each N

is an ordering

of N

. We have to show that, once chosen the next

label ℓ ∈ k

′

i+1

k, thereby determining L

′

i+1

and

′

i+1

, it is possible to choose a node

i+1

∈

N that

includes ℓ, and N

i+1

as an ordering of N

i+1

from

which ε is chosen, thereby determining L

i+1

such

that S

i+1

= S

′

i+1

Note how L

′

includes exactly i labels, while, owing to

the ε selected for nodes in N

, the number of labels in L

possibly greater than i.

ICEIS 2008 - International Conference on Enterprise Information Systems

Let N

′

be the node in N

′

= {N

′

,...,N

′

} cor-

responding to

′

i+1

. According to logical cover-

age in Deﬁnition 1, there exists a node

N =

{

,...,

′

} such that k

k ⊇ k

′

k, in other words,

includes ℓ. We consider

i+1

= N

. In order for

to be actually chosen, we have to show that each

parent node N of

in O was already considered, that

is, N belongs to the preﬁx of

N relevant to L

. Two

cases are possible for N:

(a) N is a node

∈

N . On the one hand, owing

to temporal coverage,

7→

in O entails N

′

≺

′

in O

′

. On the other, since N

′

was chosen in

′

, all its parent nodes must have been considered

already, that is, N

′

∈ h

′

,...,

′

i. Since, based

on the assumption of Induction, we always choose

for each node in N

′

∈ N

′

the corresponding node

∈

N , it is possible to claim that

was already

considered in O , that is,

∈ h

,...,

(b) N ∈ N

. We consider each path N

N in O such

that N

is the ﬁrst ancestor of N (possibly N itself),

where either N

is a root of O or N

∈

N . Let N

be the set of such ancestors. We show that each

node N

∈ N

has been considered already. Two

cases are possible: either N

∈ N

or N

∈

N . In

the ﬁrst case, N

is a node in the sterile set N

and, hence, it has been considered in N

already

(see Basis). In the second case (N

∈

N ), let

the node in

N correspondingto N

. We consider a

path

N 7→

. Since between

and

are

only nodes in N

, temporal coverage implies that

′

≺ N

′

in O

′

, where N

′

is the node in N

′

corre-

sponding to

. Thus, N

′

was already considered

in O

′

. As, based on the assumption in Induction,

we always choose in O the corresponding node of

that chosen in O

′

, this implies that

was already

considered in O too. We conclude that all nodes

in N

have been considered. Now, it is clear that

N is either in N

or N is a node belonging to the

sterile set of some node in N

. In either case, ow-

ing to the assumption of Induction, N must have

been considered already. In other words, all par-

ents of

have been chosen already, thereby al-

lowing

itself, alias

i+1

, to be chosen. Further-

more, based on the deﬁnition of sterile sequence,

we may also consider an ordering N

i+1

of N

i+1

and choose label ε for each of such nodes, thereby

leading to the conclusion that S

i+1

= S

′

i+1

. 

Note 1. Coverage is stronger than subsumption,

namely:

O ⋑ O

′

6⇒ O D O

′

. (21)

To be convinced, it sufﬁces to show an example in

which subsumption holds while coverage does not.

Consider two observations, O = (N , L , A ) and O

′

), where N = {N

}, N

′

= {N

′

L = L

′

= {a}, A = {N

7→ N

}, A

′

0, and kN

k =

k = kN

′

k = kN

′

k = {a}, as displayed in Fig. 3.

Figure 3: Observations O (left) and O

′

(right).

Clearly,

N = N and N

0. Note how, unlike O ,

since A

′

0, O

′

does not force any temporal con-

straint between N

and N

. Incidentally, both observa-

tions involvejust one candidate signature, namely S =

ha,ai. Thus, since kIsp(O )k = kIsp(O

′

)k = {ha,ai},

both observations subsume each other, in particular

O ⋑ O

′

. However, it is easy to realize that O does not

cover O

′

, namely O 6D O

′

. In fact, due to the sym-

metry of O

′

, we can choose any of the two possible

associations between nodes in O and nodes in O

′

, for

instance,

N = {N

}. Based on Deﬁnition 1, on

the one hand, both ε-coverage and logical coverage

hold. On the other, temporal coverage is missing, as

for N

7→ N

in O , we have N

′

6≺ N

′

. The same neg-

ative result occurs for

N = {N

}. In other terms,

O 6D O

′

4 TESTING COVERAGE

In this section we give an abstract, pseudo-coded

implementation of subsumption-checking via cover-

age. Speciﬁcally, Algorithm 1 tests both the neces-

sary conditions of Theorem 1 and the coverage rela-

tionship. A tracing of the algorithm on observations

in Fig. 1 is provided in Example 6.

Algorithm 1. (COVERS) The Covers function (lines

1–41) takes as input two observations, O and O

′

, and

outputs a Boolean value indicating whether or not O

covers O

′

. The body of Covers is outlined in lines

30–41. In lines 31–32, the observation parameters for

O and O

′

are set. Then, at line 33, conditions (5) and

(6) of Theorem 1, along with condition (9) of Corol-

lary 1.1, are checked. In lines 36–38, the multisets

M and M

′

of instances of labels are created, with

the former decremented by d = (n − n

′

) instances of

label ε, which is the cardinality of (N − N

′

). This

allows the algorithm to retain a sufﬁcient number of

spare nodes in N that contain ε, namely N

in Def-

inition 1. At line 39, condition (7) of Theorem 1 is

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE

SYSTEMS

checked. The algorithm yields

N , the subset of N

that is associated with N

′

in Deﬁnition 1, by build-

ing the set R of associations through the call to the

auxiliary function CovStep at line 40. The speciﬁca-

tion of CovStep is given in lines 3–29. Besides O ,

′

, M , and M

′

, it takes as input C and C

′

, the set of

nodes already considered in O and O

′

, respectively,

along with d, the number of nodes in N

not yet con-

sidered, and R , the set of associations made up so

far. The body of CovStep starts at line 10, where the

cardinality of R is tested: if R contains n

′

pairs, it

means that all nodes in N

′

have been considered and

N is completed, thereby, coverage holds. Otherwise,

a new node N

′

in O

′

is considered at line 11, such that

all its parent nodes have been considered already. At

line 12, the set F of nodes in O is created, which in-

cludes the unconsidered nodes of O with all parents

already in C . A loop for each node N in F is iterated

in lines 13–27. First, logical coverage and contain-

ment relationship of labels are tested (line 14). Then,

the set N

of the nearest ancestors

of N which have

been already involved in the associations of R is in-

stantiated (line 15). This allows temporal-coverage

checking (line 16). If the latter succeeds, CovStep is

recursively called at line 17, with new actual param-

eters: the sets C and C

′

of considered nodes are ex-

tended with N and N

′

, respectively, the multisets M

and M

′

are decremented by the labels in N and N

′

respectively, while R is extended with the new pair

(N,N

′

). If such a call succeeds, the current activation

of CovStep succeeds too (line 18). If not, or either log-

ical or temporal coverage fails, a chance still remains

by assuming N ∈ N

: this is viable only on condition

that N include ε, there exists at least one spare node

in N

(d > 0), and the multiset M contains M

′

once

decremented by the labels of N, ε aside (line 22)

. If

so, a different recursive call to CovStep is performed

at line 23, with the changed parameters being the (ex-

tended) set C of consumed nodes in O , the (decre-

mented) multiset M , and the decremented value of d.

If such a call succeeds, the current activation of Cov-

Step succeeds too. If not, the loop is iterated and a

new node in F is tried. If the computation exits the

loop in a natural way, it means that no node can be

associated with N

′

within this computational context,

thereby causing the current activation of CovStep to

fail (line 28).

The nearest ancestors of a node are not necessarily its

parents, since a parent node may not belong to R (N ), as it

is included in N

When a spare node is consumed, ε is retained in M

because. at line 38, all instances of ε relevant to spare nodes

were removed from M already.

1. function Covers(O ,O

′

): Bool

2. O = (N , L ,A ), O

′

= (N

′

): observations;

3. function CovStep(O , O

′

,C ,C

′

,M ,M

′

,d,R ): Bool

4. O = (N , L ,A ), O

′

= (N

′

): observations,

5. C ,C

′

: the set of consumed nodes for O and O

′

6. M ,M

′

: the multisets of labels in O and O

′

7. d: the number of nodes in N that can still be in N

8. R ⊆ N × N

′

: a relation on N and N

′

;

9. begin {CovStep}

10. if |R | = n

′

then return true end-if;

11. Pick up a node N

′

∈ (N

′

− C

′

) with parents in C

′

;

12. F := {N | N ∈ (N −C ), all parents of N are in C };

13. for each N ∈ F do

14. if kNk ⊇ kN

′

k ∧ (M − kNk) ⊇ (M

′

− kN

′

k) then

15. N

:= the set of nearest ancestors of N in R (N );

16. if ∀N

∈ N

,(N

′

) ∈ R (N

′

≺ N

′

) then

17. if CovStep(O ,O

′

,C ∪ {N}, C

′

∪ {N

′

},M − kNk,

′

− kN

′

k,d,R ∪ {(N,N

′

)}) then

18. return true

19. end-if

20. end-if

21. end-if;

22. if ε ∈ kNk ∧ d > 0 ∧ (M − (kNk − {ε})) ⊇ M

′

then

23. if CovStep(O ,O

′

,C ∪ {N},C

′

M − (kNk − {ε}),M

′

,d −1, R ) then

24. return true

25. end-if

26. end-if

27. end-for;

28. return false

29. end {CovStep};

30. begin{Covers}

31. n := |N |; n

:= {N | N ∈ N , ε ∈ kNk};

32. n

′

:= |N

′

|; n

′

:= {N

′

| N

′

∈ N

′

,ε ∈ kN

′

k};

33. if n < n

′

∨ n

− n

′

< n− n

′

∨ L 6⊇ L

′

then

34. return false

35. end-if:

36. Create the multisets M and M

′

of labels in O , O

′

;

37. d := n− n

′

;

38. Remove d instances of label ε from M ;

39. if M 6⊇ M

′

then return false end-if;

40. return CovStep(O ,O

′

0,M , M

′

,d,

41. end {Covers}.

Example 6. With reference to the observations in

Fig. 1, consider the run of Covers(O

). Since, ac-

cording to Example 4, all the necessary conditions of

Theorem 1 hold, we focus our attention on the ﬁrst

call to CovStep at line 40.

Depicted in Fig. 4 is the tree of the recursive ac-

tivations to CovStep, where each node i corresponds

to the i-th call (dashed nodes correspond to calls at

line 23, with the others corresponding to line 17).

Figure 4: Activation tree for CovStep in Example 6.

ICEIS 2008 - International Conference on Enterprise Information Systems

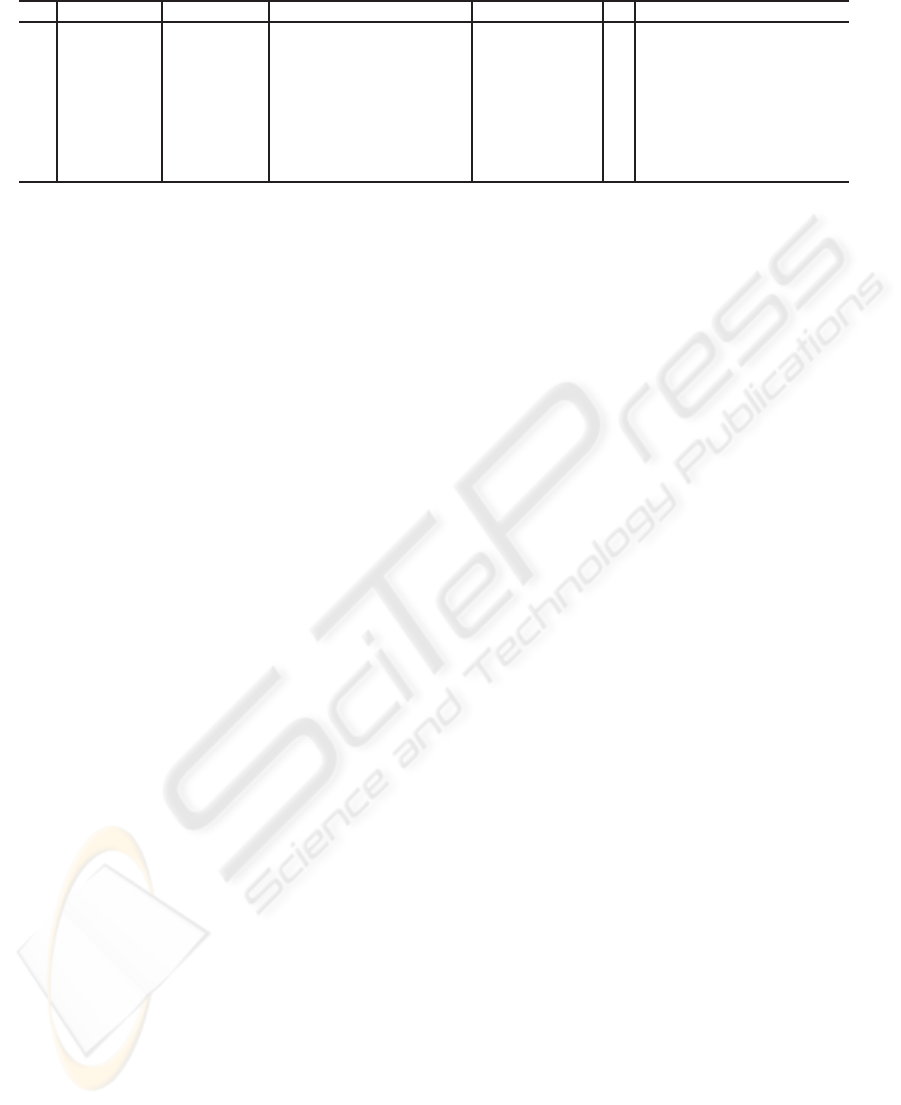
Table 1: Tracing of Covers(O

) in Example 6.

Id C C

′

M M

′

d R

0 {a,a,a,b,b,b,b,c, d, f,ε, ε} {a,a,b,c,d,ε, ε} 1

2 {1}

0 {a,a,b,b,b,c,d, f, ε,ε} {a,a,b,c,d,ε,ε} 0

3 {1,2} {1

′

} {a,b,b,c,d, f, ε,ε} {a,b,c,d,ε,ε} 0 {(2,1

′

)}

4 {2} {1

′

} {a,a,b,b,b,c,d, f, ε,ε} {a,b,c,d,ε,ε} 1 {(2,1

′

)}

5 {1,2} {1

′

} {a,b,b,c,d, f, ε} {a,c,d,ε} 1 {(2,1

′

),(1,2

′

)}

6 {1,2,3} {1

′

} {a,b,b,c,d,ε} {a,c,d,ε} 0 {(2,1

′

),(1,2

′

)}

7 {1,2,3,4} {1

′

} {a,b,ε} {a,ε} 0 {(2,1

′

),(1,2

′

),(4,3

′

)}

8 {1,2,3,4,5} {1

′

}

0 0 {(2,1

′

),(1,2

′

),(4,3

′

),(5,4

′

)}

Relevant details are given in Table 1, with Id being

the identiﬁer of the call, while the other columns in-

dicate the actual parameters of the call (observation

nodes are identiﬁed by the corresponding subscripts).

The computation is described by the following steps,

where item numbers stand for activation identiﬁers,

namely Id.

1. N

′

= 1

′

, F = {1, 2}. Within the loop (line 13),

choosing N = 1 makes the multiset containment

false (line 14). However, since condition at line 22

holds for N, a recursive call to CovStep is per-

formed at line 23 (see Id = 2 in Table 1).

2. N

′

= 1

′

, F = {2, 3}. With N = 2, a recursive call

is performed at line 17 (Id = 3 in Table 1).

3. N

′

= 2

′

, F = {3,4}. With N = 3, logical coverage

fails, as kNk 6⊇ kN

′

k. Besides, although ε ∈ kNk,

condition at line 22 is false because d = 0 (no fur-

ther spare nodes to assume in N

). Thus, a new it-

eration of loop at line 13 is performed with N = 4:

logical coverage fails, while condition at line 22 is

false (since d = 0 and ε /∈ kNk). This causes the

control to return to the second call, where condi-

tion at line 22 is false. Therefore, a new iteration

of loop at line 13 is performed, now with N = 3.

Since both checks at lines 14 and 22 fail, the con-

trol returns to the ﬁrst call, where N = 2 is cho-

sen: this allows the fourth recursive call at line 17

(Id = 4).

4. N

′

= 2

′

, F = {1, 4}. With N = 1, a recursive call

is performed at line 17 (Id = 5).

5. N

′

= 3

′

, F = {3,4}. With N = 3, logical coverage

fails. However, since condition at line 22 holds, a

recursive call is performed at line 23 (Id = 6).

6. N

′

= 3

′

, F = {4}. With N = 4, a recursive call is

performed at line 17 (Id = 7).

7. N

′

= 4

′

, F = {5}. With N = 5, a recursive call is

performed at line 17 (Id = 8).

8. At line 10, since |R | = 4, CovStep succeeds.

Proposition 1. Algorithm 1 is a sound and complete

implementation of coverage:

Covers(O ,O

′

) ⇐⇒ O D O

′

. (22)

Proof (sketch). To prove equivalence (22), we ﬁrst

show

Covers(O ,O

′

) =⇒ O D O

′

. (23)

Assuming Covers(O ,O

′

) succeeding means that the

call to CovStep at line 40 returns true. Function Cov-

Step recursively instantiates the set R of associations

of nodes (N,N

′

), for which both logical coverage (line

14) and temporal coverage (line 16), required by Def-

inition 1, hold. Moreover, ε-coverage is supported by

conditions at line 22 and the initialization at lines 36–

38, which allow for retaining the (n− n

′

) nodes of N

once R is completed (line 10). In other words, entail-

ment (23) holds. Then, we have to show

O D O

′

=⇒ Covers(O ,O

′

). (24)

The proof is by contradiction. Assume that O D O

′

while Covers(O , O

′

) = false. Based on Deﬁnition 1,

let R

∗

= {(

′

),...,(

′

)} denote the relation

between

N and N

′

. Based on a run of Covers, we

show that Covers necessarily makes up R = R

∗

. The

proof is by induction on R . Note how we can restrict

our analysis to the recursive call to CovStep, as lines

31–39 simply check the necessary conditions of

subsumption stated by Theorem 1 and Corollary 1.1.

In fact, since coverage entails subsumption (Theo-

rem 2), such conditions are necessary for coverage

too, in other words, the computation surely reaches

the call to CovStep at line 40. Moreover, such call

is supposed to return false (owing to the assumption

Covers(O ,O

′

) = false).

(Basis) Focus on the ﬁrst call to CovStep, where C ,

′

, and R are empty, and consider the (ﬁrst) node N

′

chosen at line 11. Let N

′

correspond to the j-th node

in N

′

, namely N

′

. Let

be the node in

N associated

with N

′

in R

∗

, namely (

′

) ∈ R

∗

. Based on

Deﬁnition 1, temporal coverage requires that, for

each path

in O , where all intermediate

nodes in the path are in N

, we have N

′

≺ N

′

in O

′

However, none of such paths exists, as N

′

= N

′

chosen with C

′

0, that is, N

′

has no parent nodes.

Consequently, all ancestors of

in O (if any) are

in N

, that is, they contain label ε. Since CovStep

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE

SYSTEMS

is supposed to fail, it will try all choices of N in F .

Two cases are possible: either

is a root of O or all

ancestors of

are in N

. In the ﬁrst case, N =

is associated in R with N

′

= N

′

within the recursive

call to CovStep at line 17. In the second case, the

same association will be created after a number of

recursive calls of CovStep at line 23, as all calls

to CovStep are assumed to fail (including the one

creating such association). Thus, in any case, the ﬁrst

choice of N

′

will led to an association (N,N

′

) which

is in R

∗

too.

(Induction) Assume, in the current call to CovStep,

R = {(

′

),...,(

′

)}, where R ⊂ R

∗

, that

is, all associations yielded by CovStep are in R

∗

too.

Let

and N

′

denote the projections of R on N

and N

′

, respectively. Now, consider the next choice

of N

′

at line 11. Let N

′

correspond to the j-th node in

′

, namely N

′

. Let

be the node in

N associated

with N

′

in R

∗

, namely (

′

) ∈ R

∗

. Based on

Deﬁnition 1, temporal coverage requires that, for

each path

in O , where all intermediate nodes

in the path are in N

, N

′

≺ N

′

holds in O

′

. This

implies that all N

′

are in N

′

and, in consequence of

the inductive assumption, all

are in

. Hence,

following the same argumentation outlined in Basis,

can be considered and associated with N

′

. Thus,

(

′

) is inserted into R . This leads to the claim

that (R ∪ {(

′

)}) ⊆ R

∗

, which concludes the

proof of Induction. Thus, equation (24) is proved.



5 EXPERIMENTAL RESULTS

A number of experiments were carried out in order to

assess the coverage approach to subsumption check-

ing based on different classes of observations. We ran

subsumption checking using two different algorithms

prototyped in Haskell functional language (Thomp-

son, 1999), namely Subsumes and Covers. The for-

mer is strictly based on the deﬁnition of subsumption

and requires testing index-space (automaton) contain-

ment. We considered three classes of observations,

namely disconnected, connected, and linear. In dis-

connected observations, no temporal constraints are

given among nodes, thereby maximizing temporal un-

certainty. Instead, in connected observations, each

node is temporally linked with other nodes. Linear

observations are a subclass of connected observations

where no temporal uncertainty occurs. The experi-

mental results in this paper refer to connected obser-

vations. In order to stress the computation, we chose

observations for which subsumption hold, so that the

necessary conditions in Theorem 1 always hold.

1000

2000

3000

4000

Time[s]

0 10 20

Observation nodes

Time[s]

0 10 20

Observation nodes

Figure 5: Checking subsumption: time response.

Shown in Fig. 5 is the response time for the two

algorithms, with the x-axis marked by the number of

nodes in the involved observations. Precisely, the y-

axis indicates the time for Subsumes (dashed line, on

the left) and Covers (plain line, on the right) to emit

the relevant verdict. Considering the different scale

of the y-axis, the comparison is striking in favor of

Covers. Displayed in Fig. 6 is the maximum space

allocation for the two algorithms, which shows how

no considerable difference exists between them.

Space[MB]

0 10 20

Observation nodes

Figure 6: Checking subsumption: space allocation.

6 CONCLUSIONS

A technique for checking observation-subsumptionin

diagnosis of DESs has been proposed. This check is

required to pursue similarity-based diagnosis, where

the solution of a diagnostic problem is possibly sup-

ported by the solution of a previously-solved prob-

lem stored in a knowledge-base. The solution to such

checking-problem can be provided strictly based on

the deﬁnition of observation-subsumption, which re-

quires the generation and comparison of the index

spaces of the two observations, where an index space

is an acyclic automaton. Since index-space genera-

tion and processing are computationally complex, an

alternativetechnique has been envisagedand formally

deﬁned in this paper, which exploits a number of nec-

essary conditions, as well as a sufﬁcient condition, for

In fact, when one of such conditions is violated, Covers

is increasingly more efﬁcient than Subsumes.

ICEIS 2008 - International Conference on Enterprise Information Systems

subsumption to hold. The latter is based on the notion

of coverage, which allows the direct comparison of

the two observations without any index-space gener-

ation or manipulation. The new approach has been

tested and compared with the previous (systematic)

approach. Experimental results indicate that the tech-

nique is considerably worthwhile as to time complex-

ity. However, since the implementation is based on

a pure functional language, chances are that imple-

menting it through a more efﬁcient general-purpose

language is bound to still better ﬁgures.

REFERENCES

Baroni, P., Lamperti, G., Pogliano, P., and Zanella, M.

(1999). Diagnosis of large active systems. Artiﬁcial

Intelligence, 110(1):135–183.

Brand, D. and Zaﬁropulo, P. (1983). On communicating

ﬁnite-state machines. Journal of ACM, 30(2):323–

342.

Cassandras, C. and Lafortune, S. (1999). Introduction to

Discrete Event Systems, volume 11 of The Kluwer In-

ternational Series in Discrete Event Dynamic Systems.

Kluwer Academic Publisher, Boston, MA.

Cerutti, S., Lamperti, G., Scaroni, M., Zanella, M., and

Zanni, D. (2007). A diagnostic environment for au-

tomaton networks. Software – Practice and Experi-

ence, 37(4):365–415. DOI: 10.1002/spe.773.

Chen, Y. and Provan, G. (1997). Modeling and diagnosis

of timed discrete event systems - a factory automation

example. In American Control Conference, pages 31–

36, Albuquerque, NM.

Console, L., Picardi, C., and Ribaudo, M. (2002). Process

algebras for systems diagnosis. Artiﬁcial Intelligence,

142(1):19–51.

Debouk, R., Lafortune, S., and Teneketzis, D. (2000). Co-

ordinated decentralized protocols for failure diagnosis

of discrete-event systems. Journal of Discrete Event

Dynamic Systems: Theory and Application, 10:33–86.

Hopcroft, J., Motwani, R., and Ullman, J. (2006). Introduc-

tion to Automata Theory, Languages, and Computa-

tion. Addison-Wesley, Reading, MA, third edition.

Lamperti, G. and Zanella, M. (2002). Diagnosis of discrete-

event systems from uncertain temporal observations.

Artiﬁcial Intelligence, 137(1–2):91–163.

Lamperti, G. and Zanella, M. (2003). Diagnosis of Active

Systems – Principles and Techniques, volume 741 of

The Kluwer International Series in Engineering and

Computer Science. Kluwer Academic Publisher, Dor-

drecht, NL.

Lamperti, G. and Zanella, M. (2004). A bridged diagnostic

method for the monitoring of polymorphic discrete-

event systems. IEEE Transactions on Systems, Man,

and Cybernetics – Part B: Cybernetics, 34(5):2222–

2244.

Lamperti, G. and Zanella, M. (2006a). Flexible diagnosis of

discrete-event systems by similarity-based reasoning

techniques. Artiﬁcial Intelligence, 170(3):232–297.

Lamperti, G. and Zanella, M. (2006b). Incremental pro-

cessing of temporal observations in supervision and

diagnosis of discrete-event systems. In Eighth Inter-

national Conference on Enterprise Information Sys-

tems – ICEIS’2006, pages 47–57, Paphos, Cyprus.

Lunze, J. (2000). Diagnosis of quantized systems based on

a timed discrete-event model. IEEE Transactions on

Systems, Man, and Cybernetics – Part A: Systems and

Humans, 30(3):322–335.

Pencol´e, Y. (2000). Decentralized diagnoser approach: ap-

plication to telecommunication networks. In Eleventh

International Workshop on Principles of Diagnosis –

DX’00, pages 185–192, Morelia, MX.

Pencol´e, Y. and Cordier, M. (2005). A formal framework

for the decentralized diagnosis of large scale discrete

event systems and its application to telecommunica-

tion networks. Artiﬁcial Intelligence, 164:121–170.

Roz´e, L. and Cordier, M. (2002). Diagnosing discrete-event

systems: extending the ‘diagnoser approach’ to deal

with telecommunication networks. Journal of Dis-

crete Event Dynamic Systems: Theory and Applica-

tion, 12:43–81.

Sampath, M., Lafortune, S., and Teneketzis, D. (1998). Ac-

tive diagnosis of discrete-event systems. IEEE Trans-

actions on Automatic Control, 43(7):908–929.

Sampath, M., Sengupta, R., Lafortune, S., Sinnamohideen,

K., and Teneketzis, D. (1995). Diagnosability of

discrete-event systems. IEEE Transactions on Auto-

matic Control, 40(9):1555–1575.

Sampath, M., Sengupta, R., Lafortune, S., Sinnamohideen,

K., and Teneketzis, D. (1996). Failure diagnosis using

discrete-event models. IEEE Transactions on Control

Systems Technology, 4(2):105–124.

Schullerus, G. and Krebs, V. (2001). Diagnosis of a class of

discrete-event systems based on parameter estimation

of a modular algebraic model. In Twelfth International

Workshop on Principles of Diagnosis – DX’01, pages

189–196, San Sicario, I.

Thompson, S. (1999). Haskell – The Craft of Functional

Programming. Addison-Wesley, Harlow, UK.

Zad, S., Kwong, R., and Wonham, W. (1999). Fault di-

agnosis in timed discrete-event systems. In 38th IEEE

Conference on Decision and Control – CDC’99, pages

1756–1761, Pheonix, AZ. IEEE, Piscataway, NJ.

ON CHECKING TEMPORAL-OBSERVATION SUBSUMPTION IN SIMILARITY-BASED DIAGNOSIS OF ACTIVE

SYSTEMS