A MEMETIC-GRASP ALGORITHM FOR CLUSTERING

Yannis Marinakis, Magdalene Marinaki, Nikolaos Matsatsinis and Constantin Zopounidis

Department of Production Engineering and Management, Technical University of Crete

University Campus, 73100 Chania, Greece

Keywords: Clustering analysis, Feature selection problem, Memetic Algorithms, Particle Swarm Optimization,

GRASP.

Abstract: This paper presents a new memetic algorithm, which is based on the concepts of Genetic Algorithms (GAs),

Particle Swarm Optimization (PSO) and Greedy Randomized Adaptive Search Procedure (GRASP), for

optimally clustering N objects into K clusters. The proposed algorithm is a two phase algorithm which

combines a memetic algorithm for the solution of the feature selection problem and a GRASP algorithm for

the solution of the clustering problem. In this paper, contrary to the genetic algorithms, the evolution of each

individual of the population is realized with the use of a PSO algorithm where each individual have to

improve its physical movement following the basic principles of PSO until it will obtain the requirements to

be selected as a parent. Its performance is compared with other popular metaheuristic methods like classic

genetic algorithms, tabu search, GRASP, ant colony optimization and particle swarm optimization. In order

to assess the efficacy of the proposed algorithm, this methodology is evaluated on datasets from the UCI

Machine Learning Repository. The high performance of the proposed algorithm is achieved as the algorithm

gives very good results and in some instances the percentage of the corrected clustered samples is very high

and is larger than 96%.

1 INTRODUCTION

Clustering analysis is one of the most important

problem that has been addressed in many contexts

and by researchers in many disciplines and it

identifies clusters (groups) embedded in the data,

where each cluster consists of objects that are

similar to one another and dissimilar to objects in

other clusters (Jain et al., 1999; Mirkin, 1996;

Rokach and Maimon, 2005; Xu and Wunsch II,

2005).

The typical clustering analysis consists of four

steps (with a feedback pathway) which are the

feature selection or extraction, the clustering

algorithm design or selection, the cluster validation

and the results interpretation (Xu and Wunsch II,

2005).

The basic feature selection problem (FSP) is an

optimization one, where a search through the space

of feature subsets is conducted in order to identify

the optimal or near-optimal one with respect to the

performance measure. In the literature many

successful feature selection algorithms have been

proposed (Aha and Bankert, 1996; Cantu-Paz et al.,

2004; Jain and Zongker, 1997; Marinakis et al.,

2007). Feature extraction utilizes some

transformations to generate useful and novel features

from the original ones.

The clustering algorithm design or selection step

is usually combined with the selection of a

corresponding proximity measure and the

construction of a criterion function which makes the

partition of clusters a well defined optimization

problem (Jain et al., 1999; Rokach and Maimon,

2005). Many heuristic, metaheuristic and stochastic

algorithms have been developed in order to find a

near optimal solution in reasonable computational

time. Suggestively, for example, clustering

algorithms based on Tabu Search (Liu et al., 2005),

Simulated Annealing (Chu and Roddick, 2000),

Greedy Randomized Adaptive Search Procedure

(Cano et al., 2002), Genetic Algorithms (Sheng and

Liu, 2006; Yeh and Fu, 2007); Neural Networks

(Liao and Wen, 2007), Ant Colony Optimization

(Azzag et al., 2007; Kao and Cheng, 2006; Yang and

Kamel, 2006) Particle Swarm Optimization (Kao et

al., 2007; Paterlini and Krink, 2006; Sun et al.,

2006) and Immune Systems (Li and Tan, 2006;

Younsi and Wang, 2004) have proposed in the

Marinakis Y., Marinaki M., Matsatsinis N. and Zopounidis C. (2008).

A MEMETIC-GRASP ALGORITHM FOR CLUSTERING.

In Proceedings of the Tenth International Conference on Enterprise Information Systems - AIDSS, pages 36-43

DOI: 10.5220/0001694700360043

 SciTePress

literature. An analytical survey of the clustering

algorithms can be found in (Jain et al., 1999; Rokach

and Maimon, 2005; Xu and Wunsch II, 2005).

Cluster validity analysis is the assessment of a

clustering procedure’s output using effective

evaluation standards and criteria (Jain et al., 1999;

Xu and Wunsch II, 2005). In the results

interpretation step, experts in the relevant fields

interpret the data partition in order to guarantee the

reliability of the extracted knowledge.

In this paper, a new hybrid metaheuristic

algorithm that uses a memetic algorithm (Moscato,

2003) for the solution of the feature selection

problem and a Greedy Randomized Adaptive Search

Procedure (GRASP) (Feo and Resende, 1995) for

the solution of the clustering problem is proposed.

The reason that a memetic algorithm, i.e. a genetic

algorithm with a local search phase (Moscato, 2003),

is used instead of a classic genetic algorithm is that

it is very difficult for a pure genetic algorithm to

effectively explore the solution space. A

combination of a global search optimization method

with a local search optimization method usually

improves the performance of the algorithm. In this

paper instead of using a local search method to

improve each individual separately, we use a global

search method, like Particle Swarm Optimization,

and, thus, each individual does not try to improve its

solution by itself but it uses knowledge from the

solutions of the whole population. In order to assess

the efficacy of the proposed algorithm, this

methodology is evaluated on datasets from the UCI

Machine Learning Repository. The rest of this paper

is organized as follows: In the next section the

proposed Memetic Algorithm is presented and

analyzed in detail. In section 3, the analytical

computational results for the datasets taken from the

UCI Machine Learning Repository are presented

while in the last section conclusions and future

research are given.

2 THE PROPOSED

MEMETIC-GRASP

ALGORITHM

2.1 Introduction

The proposed algorithm (MEMETIC-GRASP) for

the solution of the clustering problem is a two phase

algorithm which combines a memetic algorithm

(MA) for the solution of the feature selection

problem and a Greedy Randomized Adaptive Search

Procedure (GRASP) for the solution of the

clustering problem. In this algorithm, the activated

features are calculated by the memetic algorithm

(see section 2.4) and the fitness (quality) of each

member of the population is calculated by the

clustering algorithm (see section 2.5). In the

following, initially the clustering problem is stated,

then a general description of the proposed algorithm

is given while in the last two subsections each of the

phases of the algorithm are presented analytically.

2.2 The Clustering Problem

The problem of clustering N objects (patterns) into K

clusters is considered: Given N objects in R

allocate each object to one of K clusters such that the

sum of squared Euclidean distances between each

object and the center of its belonging cluster (which

is also to be found) for every such allocated object is

minimized. The clustering problem can be

mathematically described as follows:

Minimize

∑∑

−=

jiij

zxwzwJ

),(

(1)

subject to

, ..., N i w

1 ,1

∑

(2)

, ..., K j , ..., N, i w

11 ,1or 0 =

(3)

where:

 K is the number of clusters (given or unknown),

 N is the number of objects (given),

 x

∈ R

, (i =1,..., N) is the location of the ith

pattern (given),

 z

∈ R

, (j =1,..., K) is the center of the jth cluster

(to be found), where

∑

iij

(4)

where N

is the number of objects in the jth cluster,

 w

is the association weight of pattern x

with

cluster j, (to be found), where:

⎪

⎩

⎪

⎨

⎧

==∀

otherwise. 0

cluster toallocated ispattern if 1

, ..., K j , ..., N, i

j, i

(5)

A MEMETIC-GRASP ALGORITHM FOR CLUSTERING

2.3 General Description of the

Algorithm

Initially, as it was mentioned in the section 2.1, in

the first phase of the algorithm a number of features

are activated, using a Memetic Algorithm. Usually

in a genetic algorithm each individual of the

population is used in discrete phases. Some of the

individuals are selected as parents and by using a

crossover and a mutation operator they produce the

offspring which can replace them in the population.

But this is not what really happens in real life. Each

individual has the possibility to evolve in order to

optimize its behaviour as it goes from one phase to

the other during its life. Thus, in the proposed

memetic algorithm, the evolution of each individual

of the population is realized with the use of a PSO

algorithm. In order to find the clustering of the

samples (fitness or quality of the genetic algorithm),

a GRASP algorithm is used. The clustering

algorithm has the possibility to solve the clustering

problem with known or unknown number of

clusters. When the number of clusters is known the

Eq. (1), denoted as SSE, is used in order to find the

best clustering. In the case that the number of

clusters is unknown two additional measures are

used. The one measure is the minimization of the

distance between the centers of the clusters:

()

∑∑

−=

zzSSC .

(6)

The second measure is the minimization of a

validity index ([Ray and Turi (1999)], [Shen et al.

(2005)]) given by:

SSC

SSE

validity =

(7)

2.4 Memetic Algorithm for the Feature

Selection Problem

In this paper, a Memetic Algorithm is used for

feature selection. A Memetic Algorithm is a Genetic

Algorithm with a local search procedure (Moscatto,

2003). Genetic Algorithms (GAs) are search

procedures based on the mechanics of natural

selection and natural genetics (Holland, 1975;

Goldberg, 1989). They offer a particularly attractive

approach for problems like feature subset selection

since they are generally quite effective for rapid

global search of large, non-linear and poorly

understood spaces. A pseudocode of the proposed

algorithm is presented in the following and, then, a

short description of each phase of the Memetic-

GRASP algorithm is presented.

Initialization

Generate the initial population

Evaluate the fitness of each individual using the

GRASP algorithm for Clustering

Main Phase

Do while stopping criteria are not satisfied

Select individuals from the population to be

parents

Call crossover operator to produce offspring

Call mutation operator

Evaluate the fitness of the offspring using the

GRASP algorithm for clustering

Call PSO

Evaluate the fitness of the offspring using the

GRASP algorithm for clustering

Replace the population with the fittest of the

whole population

Enddo

In the proposed algorithm, each individual in the

population represents a candidate solution to the

feature subset selection problem. Let m be the total

number of features (from these features the choice of

the features used to represent each individual is

done). The individual (chromosome) is represented

by a binary vector of dimension m. If a bit is equal to

1 it means that the corresponding feature is selected

(activated); otherwise the feature is not selected.

This is the simplest and most straightforward

representation scheme.

The initial population is generated randomly.

Thus, in order to explore subsets of different

numbers of features, the number of 1’s for each

individual is generated randomly. In order to have

diversity of the initial population, only different

individuals are allowed. The fitness function gives

the quality of the produced member of the

population and is calculated using the GRASP

algorithm for clustering described in the following

section.

The selection mechanism is responsible for

selecting the parent chromosome from the

population and forming the mating pool. The

selection mechanism emulates the survival of- the-

fittest mechanism in nature. It is expected that a

fitter chromosome has a higher chance of surviving

on the subsequent evolution. In this work, we are

using as selection mechanism, the roulette wheel

selection (Goldberg, 1989), the 1-point crossover in

the crossover phase of the algorithm and, then, a

mutation phase (Goldberg, 1989). Afterwards, for

each offspring its fitness function is calculated.

ICEIS 2008 - International Conference on Enterprise Information Systems

In the evolution phase of the population a

Particle Swarm Optimization algorithm is used.

Particle swarm optimization (PSO) is a population-

based swarm intelligence algorithm. It was

originally proposed by (Kennedy and Eberhart,

1995) as a simulation of the social behaviour of

social organisms such as bird flocking and fish

schooling. PSO uses the physical movements of the

individuals in the swarm and has a flexible and well-

balanced mechanism to enhance and adapt to the

global and local exploration abilities. The swarm of

particles in the PSO is, usually initialized at random

but here the individuals of the population take the

place of the particles in the swarm. In each iteration,

the swarm is updated by the following equations

(Kennedy and Eberhart, 1997) applied for the

discrete binary version of PSO:

(t+1) = wυ

(t) + c

rand1 (p

− s

(t)) + c

rand2 (p

− s

(t))

(8)

)exp(1

)(

sig

−+

(9)

⎩

⎨

⎧

≥

)(3 if ,0

)(3 if ,1

)1(

sigrand

(10)

where υ

is the corresponding velocity; s

∈{0, 1} is

the current solution; p

is the best position

encountered by ith particle so far; p

represents the

best position found by any member in the whole

swarm population; t is iteration counter; rand1,

rand2 and rand3

are three uniform random numbers

in [0, 1]; w is the inertia weight; c

and c

are

acceleration coefficients. The acceleration

coefficients control how far a particle will move in a

single iteration. As in the basic PSO algorithm, a

parameter V

max

is introduced to limit υ

so that

sig(υ

) does not approach too closely 0 or 1

(Kennedy et al., 2001). Such implementation can

ensure that the bit can transfer between 1 and 0 with

a positive probability. In practice, V

max

is often set at

±4. The inertia weight w (developed by (Shi and

Eberhart, 1998)) controls the impact of previous

histories of velocities on current velocity and the

convergence behaviour of the PSO algorithm. The

particle adjusts its trajectory based on information

about its previous best performance and the best

performance of its neighbors. The inertia weight w is

updated according to the following equation:

iter

ww ×

−

−=

max

minmax

max

(11)

where w

max

, w

min

are the maximum and minimum

values that the inertia weight can take and iter

max

the maximum number of iterations (generations).

As it has, already, been mentioned in the next

generation, the fittest from the whole population (i.e.

the initial population and the offspring from

mutation, crossover and evolution phases) survives.

Thus, the population is sorted based on the fitness

function of the individuals and in the next generation

the fittest individuals survive. It must be mentioned

that the size of the population of each generation is

equal to the initial size of the population. There are

two stopping criteria for the memetic algorithm. The

one is the maximum number of generations, which is

a variable of the problem, and the other is the

genetic convergence, which means that whenever

the solutions of the genetic algorithm converge to

one solution the genetic algorithm stops.

2.5 Greedy Randomized Adaptive

Search Procedure for the

Clustering Problem

As it was mentioned earlier in the clustering phase

of the proposed algorithm a Greedy Randomized

Adaptive Search Procedure (GRASP) (Feo and

Resende, 1995; Marinakis et al., 2005; Resende and

Ribeiro, 2003) is used. GRASP is an iterative two

phase search algorithm which has gained

considerable popularity in combinatorial

optimization. Each iteration consists of two phases, a

construction phase and a local search phase. In the

construction phase, a randomized greedy function is

used to build up an initial solution. The choice of the

next element to be added is determined by ordering

all elements in a candidate list (Restricted Candidate

List – RCL) with respect to a greedy function. The

probabilistic component of a GRASP is

characterized by randomly choosing one of the best

candidates in the list but not necessarily the top

candidate. This randomized technique provides a

feasible solution within each iteration. This solution

is then exposed for improvement attempts in the

local search phase. The final result is simply the best

solution found over all iterations.

In the following, the way the GRASP algorithm

is applied for the solution of the clustering problem

is analyzed in detail. An initial solution (i.e. an

initial clustering of the samples in the clusters) is

constructed step by step and, then, this solution is

exposed for development in the local search phase of

the algorithm. The first problem that we have to face

was the selection of the number of the clusters.

Thus, the algorithm works with two different ways.

A MEMETIC-GRASP ALGORITHM FOR CLUSTERING

If the number of clusters is known a priori, then

a number of samples equal to the number of clusters

are selected randomly as the initial clusters. In this

case, as the iterations of GRASP increased the

number of clusters does not change. In each

iteration, different samples (equal to the number of

clusters) are selected as initial clusters. Afterwards,

the RCL is created. In our implementation, the best

promising candidate samples are selected to create

the RCL. The samples in the list are ordered taking

into account the distance of each sample from all

centers of the clusters and the ordering is from the

smallest to the largest distance. From this list, the

first D samples (D is a parameter of the problem) are

selected in order to form the final Restricted

Candidate List. The candidate sample for inclusion

in the solution is selected randomly from the RCL

using a random number generator. Finally, the RCL

is readjusted in every iteration by recalculated all the

distances based on the new centers and replacing the

sample which has been included in the solution by

another sample that does not belong to the RCL,

namely the (D + iter)th sample where iter is the

number of the current iteration. When all the

samples have been assigned to clusters three

measures are calculated (the best solution is

calculated based on the sum of squared Euclidean

distances between each object and the center of its

belonging cluster, see section 2.2) and a local search

strategy is applied in order to improve the solution.

The local search works as follows: For each sample

the probability of its reassignment in a different

cluster is examined by calculating the distance of the

sample from the centers. If a sample is reassigned to

a different cluster the new centers are calculated.

The local search phase stops when in an iteration no

sample is reassigned.

If the number of clusters is unknown, then,

initially a number of samples are selected randomly

as the initial clusters. Now, as the iterations of

GRASP increased the number of clusters changes

and cannot become less than two. In each iteration,

different number of clusters can be found. The

creation of the initial solutions and the local search

phase work as in the previous case. The only

difference compared to the previous case concerns

the use of the validity measure in order to choose the

best solution because as we have different number of

clusters in each iteration the sum of squared

Euclidean distances varies significantly for each

solution.

3 COMPUTATIONAL RESULTS

3.1 Data and Parameter Description

The performance of the proposed methodology is

tested on 9 benchmark instances taken from the UCI

Machine Learning Repository. The datasets were

chosen to include a wide range of domains and their

characteristics are given in Table 1 (In this Table in

the 2

column the number of observations are given,

in the 3

the number of features and the last the

number of clusters). In one case (Breast Cancer

Wisconsin) the data set is appeared with different

size of observations because in this data set there is a

number of missing values. This problem was faced

by either taking the mean values of all the

observations in the corresponding feature when all

the observations are used or by not taking into

account the observations that they had missing

values when we have less values in the observations.

Some data sets involve only numerical features and

the remaining include both numerical and

categorical features. For each data set, Table 1

reports the total number of features and the number

of categorical features in parentheses. The algorithm

was implemented in Fortran 90 and was compiled

using the Lahey f95 compiler on a Centrino Mobile

Intel Pentium M 750 at 1.86 GHz, running Suse

Linux 9.1. The parameters of the proposed algorithm

are selected after thorough testing and they are: The

number of generations of the memetic is set equal to

20; The population size is set equal to 500; The

crossover probability is set equal to 0.8; The

mutation probability is set equal to 0.25; The

number of swarms is set equal to 1; The number of

particles is set equal to 500; The number of

generations of PSO is set equal to 50; The size of

RCL varies between 50; The number of GRASP’s

iterations is equal to 100; The parameters of PSO are

= 2, c

= 2, w

max

= 0.9 and w

min

= 0.01.

Table 1: Data Sets Characteristics.

Data Sets Obser. Feat. Clus.

Australian Credit (AC) 690 14(8) 2

Breast Cancer

Wisconsin 1 (BCW1)

699 9 2

Breast Cancer

Wisconsin 2 (BCW2)

683 9 2

Heart Disease (HD) 270 13(7) 2

Hepatitis 1 (Hep1) 155 19 (13) 2

Ionosphere (Ion) 351 34 2

Spambase (Spam) 4601 57 2

Iris 150 4 3

Wine 178 13 3

ICEIS 2008 - International Conference on Enterprise Information Systems

3.2 Results of the Proposed Algorithm

The objective of the computational experiments is to

show the performance of the proposed algorithm in

searching for a reduced set of features with high

clustering of the data. Because of the curse of

dimensionality, it is often necessary and beneficial

to limit the number of input features in order to have

a good predictive and less computationally intensive

model. In general there are 2

number of features

-1 possible

feature combinations and, thus, in our cases the most

difficult problem is the Spambase where the number

of feature combinations is 2

-1.

A comparison with other metaheuristic

approaches for the solution of the clustering problem

is presented in Table 2. In this Table, seven other

algorithms are used for the solution of the feature

subset selection problem and for the clustering

problem. In the first group of algorithms in this

Table, a PSO algorithm is used for the solution of

the feature selection problem while a GRASP is

used in the clustering phase (columns 4 and 5 of

Table 2), an Ant Colony Optimization Algorithm

(Dorigo and Stützle, 2004) is used for the feature

selection problem with GRASP in the clustering

phase (columns 6 and 7 of Table 2) and a genetic

algorithm is used in the first phase of the algorithm

while a GRASP is used in the second phase of the

algorithm (columns 8 and 9 of Table 2). In the

second group of algorithms and in columns 2 and 3

of Table 2, a Tabu Search Algorithm (Glover, 1989)

is used in the first phase and a GRASP is used in the

second phase, in columns 4 and 5 of Table 2 a PSO

is used in the first phase and an Ant Colony

Optimization algorithm is used in the second phase,

in columns 6 and 7 of Table 2 of the second group in

both phases (feature selection phase and clustering

phase) an Ant Colony Optimization algorithm is

used while in columns 8 and 9 of Table 2 of the

second group a PSO is used in both phases (feature

selection phase and clustering phase).

From this table, it can be observed that the

Memetic-GRASP algorithm performs better (has the

largest number of correct clustered samples) than the

other seven algorithms in all instances. It should be

mentioned that in some instances the differences in

the results between the Memetic-GRASP algorithm

and the other seven algorithms are very significant.

Mainly, for the two data sets that have the largest

number of features compared to the other data sets,

i.e. in the Ionosphere data set the percentage of

corrected clustered samples for the Memetic-

GRASP algorithm is 86.89% while for all the other

methods the percentage varies between 73.50% to

86.03%, and in the Spambase data set the percentage

of corrected clustered samples for the Memetic-

GRASP algorithm is 87.35% while for all the other

methods the percentage varies between 82.80% to

87.19%. It should, also, be noted that a hybridization

algorithm performs always better than a no

hybridized algorithm. More precisely, the only three

algorithms that are competitive in almost all

instances with the proposed Memetic-GRASP

algorithm are the Hybrid PSO - ACO, the Hybrid

PSO - GRASP and the Hybrid ACO - GRASP

algorithms. These results prove the significance of

the solution of the feature selection problem in the

clustering algorithm as when more sophisticated

methods for the solution of this problem were used

the performance of the clustering algorithm was

improved. The significance of the solution of the

feature selection problem using the Memetic

Algorithm is, also, proved by the fact that with this

algorithm the best solution was found by using

fewer features than the other algorithms used in the

comparisons. More precisely, in the most difficult

instance, the Spambase instance, the proposed

algorithm needed 32 features in order to find the

optimal solution, while the other seven algorithms

the algorithms needed between 34 - 56 features to

find their best solution. A very significant

observation is that the results of the proposed

Memetic-GRASP algorithm are better than those

obtained when a classic genetic algorithm was used.

The percentage in the correct clustered instances in

the Memetic-GRASP algorithm is 0.15% to 11.11%

greater than the percentage in the genetic algorithm.

It should, also, be mentioned that the algorithm was

tested with two options: with known and unknown

number of clusters. When the number of clusters

was unknown and, thus, in each iteration of the

algorithm different initial values of clusters were

selected the algorithm always converged to the

optimal number of clusters and with the same results

as in the case that the number of clusters was known.

4 CONCLUSIONS

In this paper a new metaheuristic algorithm is

proposed for solving the Clustering Problem. This

algorithm is a two phase algorithm which combines

a memetic algorithm for the solution of the feature

selection problem and a Greedy Randomized

Adaptive Search Procedure (GRASP) for the

solution of the clustering problem. The performance

A MEMETIC-GRASP ALGORITHM FOR CLUSTERING

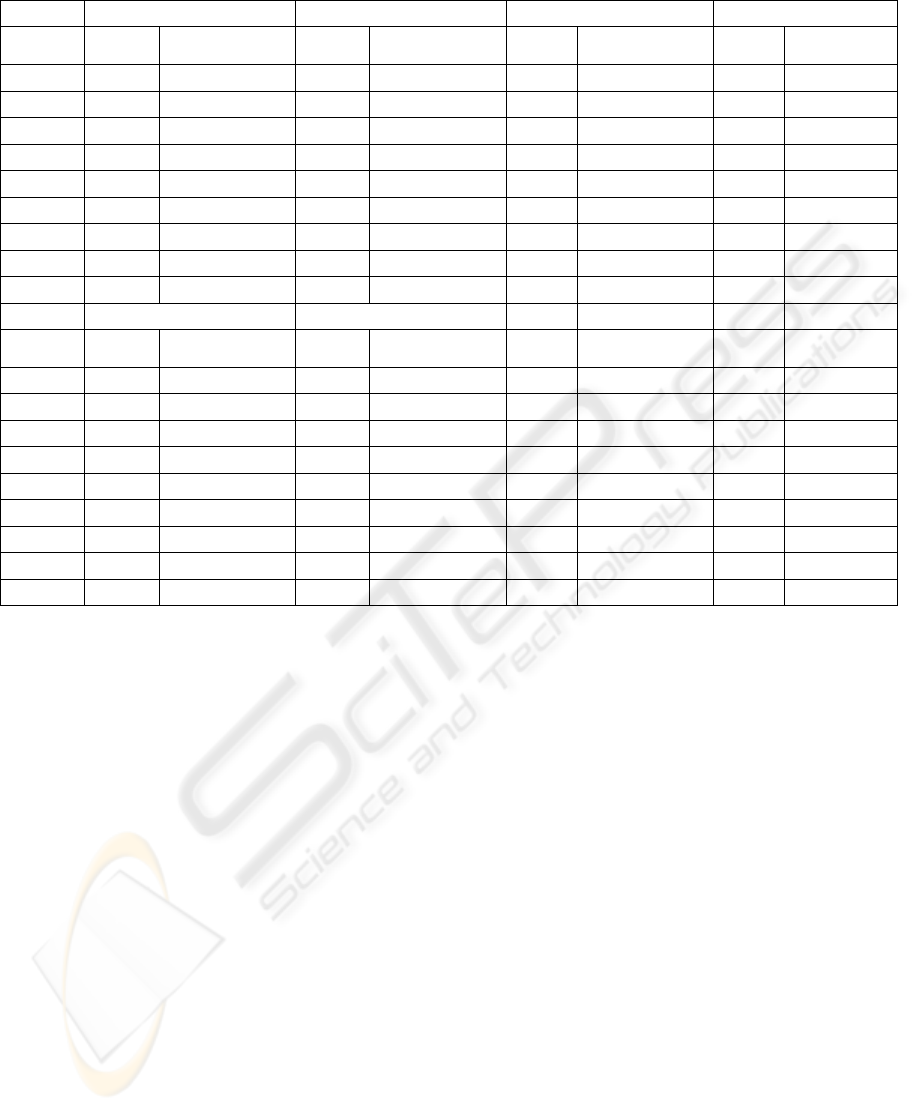
Table 2: Results of the Algorithms.

Method

Memetic-GRASP

PSO-GRASP ACO-GRASP Genetic-GRASP

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

BCW2 5 664(97.21%) 5 662(96.92%) 5 662(96.92%) 5 662(96.92%)

Hep1 9 139(89.67%) 7 135(87.09%) 9 134(86.45%) 9 134(86.45%)

AC 8 604(87.53%) 8 604(87.53%) 8 603(87.39%) 8 602(87.24%)

BCW1 8 677(96.85%) 5 676(96.70%) 5 676(96.70%) 5 676(96.70%)

Ion 5 305(86.89%) 11 300(85.47%) 2 291(82.90%) 17 266(75.78%)

spam 32 4019(87.35%) 51 4009(87.13%) 56 3993(86.78%) 56 3938(85.59%)

HD 9 236(87.41%) 9 232(85.92%) 9 232(85.92%) 7 231(85.55%)

Iris 3 146(97.33%) 3 145(96.67%) 3 145(96.67%) 4 145(96.67%)

Wine 7 176(98.87%) 7 176(98.87%) 8 176(98.87%) 7 175(98.31%)

Method Tabu-GRASP PSO-ACO ACO PSO

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

Sel.

Feat. Cor. Clust.

BCW2 6 661(96.77%) 5 664(97.21%) 5 662(96.92%) 5 662(96.92%)

Hep1 10 132(85.16%) 6 139(89.67%) 9 133(85.80%) 10 132(85.16%)

AC 9 599(86.81%) 8 604(87.53%) 8 601(87.10%) 8 602(87.24%)

BCW1 8 674(96.42%) 5 677(96.85%) 8 674(96.42%) 8 674(96.42%)

Ion 4 263(74.92%) 7 302(86.03%) 16 258(73.50%) 12 261(74.35%)

spam 34 3810(82.80%) 39 4012(87.19%) 41 3967(86.22%) 37 3960(86.06%)

HD 9 227(84.07%) 9 235(87.03%) 9 227(84.07%) 9 227(84.07%)

Iris 3 145(96.67%) 3 146(97.33%) 3 145(96.67%) 3 145(96.67%)

Wine 7 174(97.75%) 7 176(98.87%) 7 174(97.75%) 7 174(97.75%)

of the proposed algorithm was tested using various

benchmark datasets from UCI Machine Learning

Repository. The proposed algorithm gave very

efficient results in all instances and the significance

of the solution of the clustering problem by the

proposed algorithm is proved by the fact that the

percentage of the correct clustered samples is very

high and in some instances is larger than 97% and

by the fact that the instances with the largest number

of features gave better results when the Memetic-

GRASP algorithm was used.

ACKNOWLEDGEMENTS

This work is a deliverable of the task KP_26 and is

realized in the framework of the Operational

Programme of Crete, and it is co-financed from the

European Regional Development Fund (ERDF) and

the Region of Crete with final recipient the General

Secretariat for Research and Technology.~

REFERENCES

Aha, D.W., and Bankert, R.L., 1996. A Comparative

Evaluation of Sequential Feature Selection

Algorithms. In Artificial Intelligence and Statistics,

Fisher, D. and J.-H. Lenx (Eds.). Springer-Verlag,

New York.

Azzag, H., Venturini, G., Oliver, A., Gu, C., 2007. A

Hierarchical Ant Based Clustering Algorithm and its

Use in Three Real-World Applications, European

Journal of Operational Research, 179, 906-922.

Cano, J.R., Cordón, O., Herrera, F., Sánchez, L., 2002. A

GRASP Algorithm for Clustering, In IBERAMIA

2002, LNAI 2527, Garijo, F.J., Riquelme, J.C. and M.

Toro (Eds.). Springer-Verlag, Berlin Heidelberg, 214-

223.

Cantu-Paz, E., Newsam, S., Kamath C., 2004. Feature

Selection in Scientific Application, In Proceedings of

the 2004 ACM SIGKDD International Conference on

Knowledge Discovery and Data Mining, 788-793.

Chu, S., Roddick, J., 2000. A Clustering Algorithm Using

the Tabu Search Approach with Simulated Annealing.

In Data Mining II-Proceedings of Second

International Conference on Data Mining Methods

and Databases, Ebecken, N. and C. Brebbia (Eds.).

Cambridge, U.K., 515-523.

ICEIS 2008 - International Conference on Enterprise Information Systems

Dorigo, M, Stützle, T., 2004. Ant Colony Optimization. A

Bradford Book, The MIT Press, Cambridge,

Massachusetts, London, England.

Feo, T.A., Resende, M.G.C., 1995. Greedy Randomized

Adaptive Search Procedure, Journal of Global

Optimization, 6, 109-133.

Glover, F., 1989. Tabu Search I, ORSA Journal on

Computing, 1 (3), 190-206.

Glover, F., 1990. Tabu Search II, ORSA Journal on

Computing, 2 (1), 4-32.

Goldberg, D. E., 1989. Genetic Algorithms in Search,

Optimization, and Machine Learning, Addison-

Wesley Publishing Company, INC. Massachussets.

Holland, J.H., 1975. Adaptation in Natural and Artificial

Systems, University of Michigan Press, Ann Arbor,

MI.

Jain, A., Zongker D., 1997. Feature Selection: Evaluation,

Application, and Small Sample Performance, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, 19, 153-158.

Jain, A.K., Murty, M.N., Flynn, P.J., 1999. Data

Clustering: A Review, ACM Computing Surveys, 31

(3), 264-323.

Kao, Y., Cheng, K., 2006. An ACO-Based Clustering

Algorithm, In ANTS 2006, LNCS 4150, M. Dorigo et

al. (Eds.). Springer-Verlag, Berlin Heidelberg, 340-

347.

Kennedy, J., Eberhart, R., 1995. Particle swarm

optimization. In Proceedings of 1995 IEEE

International Conference on Neural Networks, 4,

1942-1948.

Kennedy, J., Eberhart, R., 1997. A discrete binary version

of the particle swarm algorithm. In Proceedings of

1997 IEEE International Conference on Systems,

Man, and Cybernetics, 5, 4104-4108.

Kennedy, J., Eberhart, R., Shi, Y., 2001. Swarm

Intelligence. Morgan Kaufmann Publisher, San

Francisco.

Li, Z., Tan, H.-Z., 2006. A Combinational Clustering

Method Based on Artificial Immune System and

Support Vector Machine, In KES 2006, Part I, LNAI

4251, Gabrys, B., Howlett, R.J. and L.C. Jain (Eds.).

Springer-Verlag Berlin Heidelberg, 153-162.

Liao, S.-H., Wen, C.-H., 2007. Artificial Neural Networks

Classification and Clustering of Methodologies and

Applications – Literature Analysis from 1995 to 2005,

Expert Systems with Applications, Vol. 32, pp. 1-11.

Liu, Y., Liu, Y., Wang, L., Chen, K., 2005. A Hybrid

Tabu Search Based Clustering Algorithm, In KES

2005, LNAI 3682, R. Khosla et al. (Eds.). Springer-

Verlag, Berlin Heidelberg, 186-192.

Marinakis, Y., Migdalas, A., Pardalos, P.M., 2005.

Expanding Neighborhood GRASP for the Traveling

Salesman Problem, Computational Optimization and

Applications, 32, 231-257.

Marinakis Y., Marinaki, M., Doumpos, M., Matsatsinis,

N., Zopounidis, C., 2007. Optimization of Nearest

Neighbor Classifiers via Metaheuristic Algorithms for

Credit Risk Assessment, Journal of Global

Optimization, (accepted).

Mirkin, B., 1996. Mathematical Classification and

Clustering, Kluwer Academic Publishers, Dordrecht,

The Netherlands.

Moscato, P., Cotta C., 2003. A Gentle Introduction to

Memetic Algorithms. In Handbooks of Metaheuristics,

Glover, F., and G.A., Kochenberger (Eds.). Kluwer

Academic Publishers, Dordrecht, 105-144.

Paterlini, S., Krink, T., 2006. Differential Evolution and

Particle Swarm Optimisation in Partitional Clustering,

Computational Statistics and Data Analysis, 50,

1220-1247.

Ray, S., Turi, R.H., 1999. Determination of Number of

Clusters in K-means Clustering and Application in

Colour Image Segmentation. In Proceedings of the 4th

International Conference on Advances in Pattern

Recognition and Digital Techniques (ICAPRDT99),

Calcutta, India.

Resende, M.G.C., Ribeiro, C.C., 2003. Greedy

Randomized Adaptive Search Procedures. In

Handbooks of Metaheuristics, Glover, F., and G.A.,

Kochenberger (Eds.). Kluwer Academic Publishers,

Dordrecht, 219-249.

Rokach, L., Maimon, O., 2005. Clustering Methods, In

Data Mining and Knowledge Discovery Handbook,

Maimon, O. and L. Rokach (Eds.). Springer, New

York, 321-352.

Shen, J., Chang, S.I., Lee, E.S., Deng, Y., Brown, S.J.,

2005. Determination of Cluster Number in Clustering

Microarray Data, Applied Mathematics and

Computation, 169, 1172-1185.

Sheng, W., Liu, X., 2006. A Genetic k-Medoids

Clustering Algorithm, Journal of Heuristics, 12, 447-

466.

Shi, Y., Eberhart, R. 1998. A modified particle swarm

optimizer. In Proceedings of 1998 IEEE World

Congress on Computational Intelligence, 69-73.

Sun, J., Xu, W., Ye, B., 2006. Quantum-Behaved Particle

Swarm Optimization Clustering Algorithm, In ADMA

2006, LNAI 4093, Li, X., Zaiane, O.R. and Z. Li

(Eds.). Springer-Verlag, Berlin Heidelberg, 340-347.

Xu, R., Wunsch II, D., 2005. Survey of Clustering

Algorithms, IEEE Transactions on Neural Networks,

16 (3), 645-678.

Yang, Y., Kamel, M.S., 2006. An Aggregated Clustering

Approach Using Multi-Ant Colonies Algorithms,

Pattern Recognition, 39, 1278-1289.

Yeh, J.-Y., Fu, J.C., 2007. A Hierarchical Genetic

Algorithm for Segmentation of Multi-Spectral Human-

Brain MRI, Expert Systems with Applications,

doi:10.1016/j.eswa.2006.12.012.

Younsi, R., Wang, W., 2004. A New Artificial Immune

System Algorithm for Clustering, In IDEAL 2004,

LNCS 3177, Z.R. Yang et al. (Eds.). Springer-Verlag,

Berlin Heidelberg, 58-64.

A MEMETIC-GRASP ALGORITHM FOR CLUSTERING