WORKFLOW TREES FOR REPRESENTATION AND MINING OF

IMPLICITLY CONCURRENT BUSINESS PROCESSES

Daniel Nikovski

Mitsubishi Electric Research Laboratories, 201 Broadway, Cambridge, U.S.A.

Keywords:

Business process management, Process mining, Petri nets.

Abstract:

We propose a novel representation of business processes called workﬂow trees that facilitates the mining of

process models where the parallel execution of two or more sub-processes has not been recorded explicitly in

workﬂow logs. Based on the provable property of workﬂow trees that a pair of tasks are siblings in the tree

if and only if they have identical respective workﬂow-log relations with each and every remaining third task

in the process, we describe an efﬁcient business process mining algorithm of complexity only cubic in the

number of process tasks, and analyze the class of processes that can be identiﬁed and reconstructed by it.

1 INTRODUCTION

The organization and optimization of business pro-

cesses within an enterprise is essential to the success

of that enterprise in the marketplace, and the explicit

management of business processes within dedicated

software suites has emerged as an important class of

information technology (van der Aalst and van Hee,

2002). Key to the successful management of business

processes is the nature of the models used for pro-

cess representation, construction, maintenance, and

improvement. Whereas some kind of graphical repre-

sentation has been used almost universally, the types

of proposed models and the semantics associated with

them have varied widely. Some of the more popu-

lar representations include Petri nets (van der Aalst

et al., 2004), ﬁnite state machines and Markov models

(Cook and Wolf, 1998a), as well as special-purpose

graphic formalisms such as AND/OR trees (Silva

et al., 2005) and block diagrams (Schimm, 2004). In

most cases, these graphic representations are also as-

sociated with a corresponding formal language that is

interpretable by BPM sequencing middleware. For an

extensive comparison between business process mod-

eling formalisms from several perspectives, see, for

example (List and Korherr, 2006).

The abundance of modeling formalisms suggests

that there isn’t a single best representation, but rather,

multiple trade-offs exist when adapting formalisms to

a particular task, and the wide choice of available for-

malisms is in fact beneﬁcial. The speciﬁc task of in-

terest addressed in this paper is the learning from data

of representations for processes with implicit concur-

rency. We propose a solution to this problem in the

form of a novel representation for business processes,

and an associated algorithm for mining such mod-

els from data with very favorable computational com-

plexity (cubic in the number of process tasks).

2 PROCESS MINING AND

IMPLICIT CONCURRENCY

The objective of process mining algorithms and sys-

tems is to construct an explicit process model from

recorded event logs (van der Aalst and Weijters,

2004). This functionality is especially useful when

a new business process management (BPM) system

is deployed at a customer site and explicit models

of the existing processes have to be produced as a

starting point for analysis, process re-engineering,

etc. The traditional alternative to process mining

— the manual construction of process models, usu-

ally using graphic editors — can be very time- and

labor-intensive, because it typically involves inter-

views with executives, and also very imprecise, be-

cause humans can only describe the way they imag-

ine business processes operate, and not the way these

business processes actually operate. At the same time,

if the business processes already involve information

technology (e.g. enterprise resource planning sys-

Nikovski D. (2008).

WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS PROCESSES.

In Proceedings of the Tenth International Conference on Enterpr ise Information Systems - ISAS, pages 30-36

DOI: 10.5220/0001671900300036

 SciTePress

tems, customer relationship management systems), in

all likeliness, abundant execution logs from these sys-

tems already exist. In such cases, using these execu-

tion logs to automatically extract process models can

result in major savings in time and effort and improve

model accuracy signiﬁcantly.

The objective of process mining is to ﬁnd a model

of a business process (represented in a suitable for-

malism) solely by inspecting the relative order of

tasks as manifested in logs collected from the re-

peated execution of the business process. It is as-

sumed that N different tasks t

, i = 1, N, t

∈ T from

the set T can be distinguished in the execution log.

The workﬂow logs are divided into disjoint episodes

that correspond to the processing of one work case

each. During one episode, the case takes one possible

path through the process. An episode is represented

as a sequence of tasks, and indicates the sequential

order in which a particular case was processed. The

objective of process mining algorithms, then, is to in-

spect the entire workﬂow log and induce a process

model that could have produced this log. It is usu-

ally desired that the induced model be as compact as

possible, and have no duplicate tasks.

Initial research recognized that process mining is

a special case of inductive machine learning (ML),

hence generic ML techniques, most commonly based

on heuristic search, are applicable to this problem.

Early examples of this approach included the algo-

rithms of Cook and Wolf (Cook and Wolf, 1998a;

Cook and Wolf, 1998b), which employed greedy in-

duction over model spaces representing Markov mod-

els and Petri nets. While successful, the heuristic na-

ture of search in model spaces does not guarantee the

discovery of the optimal model, where optimality is

usually deﬁned as a trade-off between model accuracy

and parsimony. Further complicating the problem of

ﬁnding the optimal model is the issue of data sufﬁ-

ciency — certainly, if the exact relationship among

tasks is not manifested in the execution logs, a correct

(and much less, optimal) model cannot be mined from

these logs.

A major shift from heuristic search and inductive

methods occurred with the emergence of constructive

algorithms, such as α, α+, and β (van der Aalst et al.,

2004; de Medeiros et al., 2004). These algorithms

pre-compute the relations between each pair of tasks

as manifested in the execution log and organize the

identiﬁed relations in a tabular format. After that, the

algorithms construct a model based on this relations

table only, without having to examine the execution

log ever again.

Perhaps the best known example of this class of

constructive algorithms is the α algorithm proposed

by van der Aalst et al., 2004. The business process

representation used by this algorithm is structured

workﬂow nets (SWF-nets) — a carefully chosen and

precisely deﬁned subset of Petri nets that avoids unde-

sirable situations such as deadlocks, incomplete tasks,

indeterminate synchronization, etc.

A signiﬁcant novel idea of the α algorithm is to

pre-process the execution log and determine the pair-

wise relations between all pairs of tasks. These so

called log-based ordering relations between a pair of

tasks a and b are as follows:

• a > b iff there exists at least one episode of the log

where a is encountered immediately before b,

• a → b iff a > b and b 6 >a,

• a#b iff a 6 >b and b 6 >a, and

• a k b iff a > b and b > a.

The assumption of these algorithms is that the sup-

plied workﬂow log is complete, i.e. it reﬂects cor-

rectly the relations between the tasks in the real pro-

cess that produced the log. This assumption is rea-

sonable for most execution logs collected from real

enterprise information systems. Once the relation be-

tween each pair of tasks has been identiﬁed to be one

of these four relations, the algorithm proceeds to con-

struct a minimal SWF-net that satisﬁes the relations.

Based on the provable property that a → b implies that

a SWF-net place exists immediately between tasks a

and b, van der Aalst et al., 2004 devised an algorithm

that builds an SWF-net in eight steps, without any

heuristic search.

The α algorithm is able to mine a large class

of SWF-nets. However, one important limitation of

the α algorithm and its derivatives is that they can-

not detect all cases of concurrency in a business pro-

cess. Concurrent tasks in SWF-nets are represented

by means of a construct involving auxiliary AND-

split and AND-join tasks (cf. Fig. 1). We will refer

to this construct as an AND-block. If we compare it

to the case of task choice (exclusive OR, or an OR-

block), where only one of several tasks is executed,

it is evident that an OR-block involves no such aux-

iliary tasks (cf. Fig. 2). The α algorithm can mine

processes with AND-blocks as long as the two aux-

iliary tasks, the AND-split and the AND-join, have

been recorded explicitly in the workﬂow log. We will

call such processes explicitly concurrent, i.e., when

concurrency is present, the initiation and completion

of parallel execution is explicit in the log.

However, it cannot be expected that workﬂow logs

would contain explicit AND-splits and AND-joins,

because they do not correspond to actual tasks in the

problem domain — whenever parallel execution has

WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS

PROCESSES

&-s

&-j

Figure 1: A WF-net for representing parallel execution:

tasks A and B are executed concurrently. Here the tasks

labeled &-s and &-j are auxiliary and have the sole purpose

of explicitly specifying concurrency.

Figure 2: A WF-net for representing exclusive choice: ei-

ther task A or task B is executed, but not both.

been performed in a given legacy IT system, the de-

cision to initiate it and the logic to synchronize its

completion is usually buried somewhere deep into ex-

ecutable code, and it is precisely the objective of the

process mining algorithm to extract it and model it

explicitly.

When explicit AND-splits and AND-joins are ab-

sent from the workﬂow ﬁle (which we expect to be the

typical situation), the mining algorithm would have to

deal with implicitly concurrent business processes. In

numerous cases, the α algorithm and its descendants

would have difﬁculties in handling implicit concur-

rency. One speciﬁc instantiation of this problem is

when an AND-block is nested within an OR-block.

For example, van der Aalst, 2004 discussed the pro-

cess in Fig. 3, and concluded that if the synchroniz-

ing AND-split and AND-join tasks were not present

in the workﬂow log, the exact workﬂow net could not

be recovered by the α algorithm.

The reason why implicit concurrency is challeng-

ing for the α algorithm and its descendants is that

they never create new tasks other than those already

present in the workﬂow log, and hence cannot create

the explicit AND-blocks necessary to represent con-

currency in the SWF net formalism. This suggests

that perhaps it would be worthwhile to explore alter-

native representations and mining algorithms that can

&-s

&-j

Figure 3: This WF-net that cannot be recovered by the α

algorithm, if the auxiliary tasks &-s and &-j are missing

from the workﬂow log.

handle implicit concurrency better, while still aiming

at constructive solutions that build compact relation

tables from workﬂow logs. Another desirable prop-

erty of such algorithms would be more favorable com-

putational complexity — the run time of the α algo-

rithm and its derivatives is exponential in the number

of tasks N, since they involve search within the space

of all pairs of sets of tasks, i.e. the powerset of the

set of all tasks. For practical purposes, a mining algo-

rithm of low-degree polynomial complexity would be

much more desirable.

3 WORKFLOW TREES FOR

REPRESENTATION OF

BUSINESS PROCESSES

We propose a representation of business processes

that is based on the natural hierarchical organization

of work in most enterprises. The representation is

in the form of an ordered tree, where the leaves of

the tree represent tasks, and the internal nodes of the

tree represent the functional blocks in which these

tasks are organized. This representation is similar to

the block representation used by Schimm (Schimm,

2004) and the AND-OR graphs proposed by Silva et

al. (Silva et al., 2005) in the type of the blocks used.

Based on its hierarchical organization, it is also close

to the way sub-diagrams can be deﬁned in UML 2.0

Activity Diagrams.

In this paper, we will consider trees that have four

building blocks, labeled as follows: parallel (AND),

choice (OR), sequence (SEQ), and iteration (ITER).

The meaning of the AND and OR blocks is as shown

in Figs. 1 and 2, in Petri net notation. The meaning

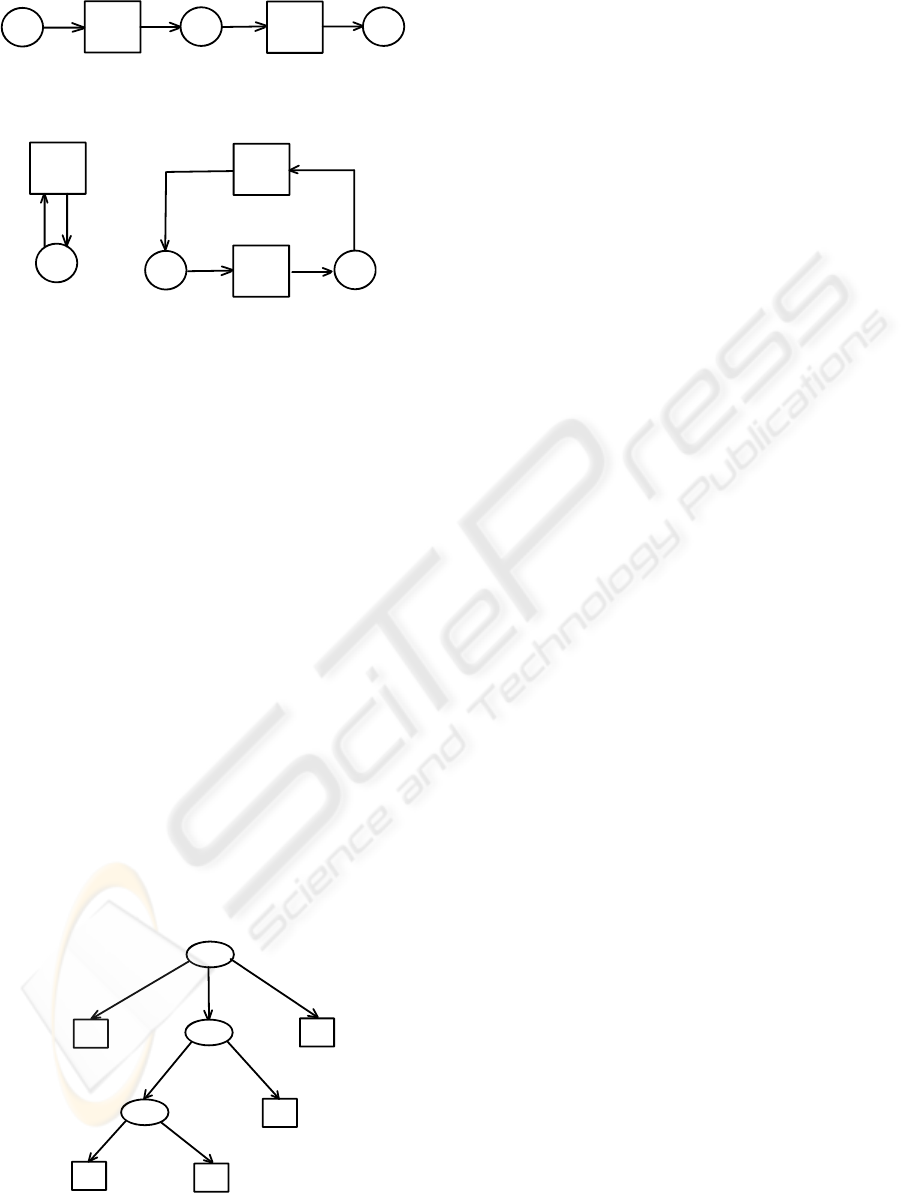
of the SEQ construct is obvious, and is shown in Fig.

4. For the iteration construct, two deﬁnitions are pos-

sible, depending on whether zero executions of a task

are allowed, or it has to be executed at least once. The

two alternative deﬁnitions are shown in Fig. 5.

These constructs are very similar to those used in

van der Aalst and van Hee, 2002 (with the exception

of the iteration construct, which must involve at least

two tasks there). It has been shown that by starting

with one of these constructs, and recursively substi-

tuting its component tasks with compound blocks of

more tasks, a large class of sound and safe nets can be

constructed. Our proposal for workﬂow trees formal-

izes this intuition: the structure of the tree prescribes

the steps that must be taken during this process of top-

down recursive construction of a business process. It

also describes a way to convert a workﬂow tree (WF-

tree) into a SWF-net: by traversing the WF-tree in

ICEIS 2008 - International Conference on Enterprise Information Systems

Figure 4: A WF-net that speciﬁes sequential execution:

tasks A and B are always executed strictly in this order.

Figure 5: Two possible WF-nets that specify iterative exe-

cution. The net on the left allows zero or more executions

of task A, while the net on the right speciﬁes that task B

should be executed at least once (and possibly many more

times).

any convenient order, each tree node is replaced by

its corresponding Petri net, as described above, and if

any of the children of this node are nodes themselves,

the procedure is recursively repeated until all tasks in

the resulting SWF-net are atomic tasks. As an exam-

ple, Fig. 6 shows the WF-tree that would result in the

SWF-net previously shown in Fig. 3, if expanded as

described.

While this general approach to constructing busi-

ness process models is intuitive and has been explored

before, the speciﬁc representation in a tree-like form

that we propose allows us to analyze and identify the

properties of this representation that are useful for the

purposes of process mining. In particular, we are in-

terested in the relations between pairs of tasks that are

entailed by this representation. We deﬁne a set of re-

lations AND, OR, SEQ, and IT ER that are n-ary, and

can hold between two or more tasks. Two tasks in

the WF tree have one of these relations between each

other. (In this case, the relation is binary.) We specify

SEQ

AND

Figure 6: A workﬂow tree that corresponds to the WF-net

from Fig. 3.

that the binary relation between a pair of tasks in a

WF-tree is determined by the node of the tree that is

the least common ancestor (LCA) of these two tasks.

For example, for the SWF-net in Fig. 3 (respectively,

the tree in Fig. 6), the tasks A and E are in the SEQ

relation, and B and E are in the OR relation.

In the general case, it would be possible to have

process models with nested blocks of the same type,

for example an OR block nested immediately within

another OR block. In the corresponding WF-tree, this

would be expressed as one OR node having as a child

(direct descendant) another OR node. While certainly

possible and valid, such WF-trees are redundant, and

it is usually desirable to eliminate this redundancy.

We deﬁne a compact workﬂow tree (CWF-tree) to be

a workﬂow tree where no two nodes of the same label

have a direct parent/child relationship.

Before analyzing the properties of the described

relations, we will note that as a corollary of this spec-

iﬁcation and the nature of our speciﬁc deﬁnition of an

iterative block, no two tasks can be in the IT ER re-

lation. This is due to the fact that a tree node labeled

with ITER always has only one child, and hence can-

not be the LCA of any pair of distinct tasks. (This

is true regardless of which alternative deﬁnition of an

ITER block is chosen from the two shown in Fig. 5).

The remaining three relations have the following

properties. When these relations are binary, the binary

AND and OR are transitive and symmetric, while the

binary SEQ is transitive and asymmetric ((aSEQb) ⇒

¬(bSEQa)). Ternary relations can be deﬁned by

aRb ∧ bRc ⇒ R(a, b, c), whereas relations of arbi-

trary arity have the property that R(a

, a

, . . . , a

n−1

) ∧

n−1

⇒ R(a

, a

, . . . , a

n−1

, a

). Here R can be any

of the three relations AND, OR, and SEQ. Note that

in combination with the asymmetry of the binary SEQ

relation, the n-ary SEQ relation is guaranteed to hold

only between arguments in the correct order, while the

symmetry of the binary AND and OR ensure that their

n-ary counterparts hold for an arbitrary order of their

arguments. For the sake of analytical convenience, we

will also deﬁne the symmetric relation LIN, such that

aLINb iff aSEQb∨bSEQa. The meaning of this rela-

tion is linear order — it holds true between two tasks

when one of them follows the other.

Note also that if three or more tasks are in the

same relation, it is not necessarily true that each pair

of them has the same LCA — since more than one

tree node can be labeled with the same block label,

it is completely possible that three or more tasks are

in the same relation, but are not descendants of three

different children of the same node.

What is true, though, is that any three tasks a,

b, and c of the same WF-tree can have at most two

WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS

PROCESSES

distinct relations R

, R

from the set {AND, OR, LIN}

among them.

Lemma 1. aR

b ∧ bR

c ⇒ aR

c ∨ aR

c, for R

, R

∈

{AND, OR, LIN}.

Proof. For full proof, see the accompanying online

technical report (Nikovski and Baba, 2007).

Furthermore, due to the symmetry of the three re-

lations AND, OR, and LIN, the lemma holds for all

possible symmetric exchanges in the order of tasks in

these relations. A direct corollary of this lemma (in

one respective instantiation as regards relation sym-

metry) is that if two tasks a and b are in relation R

(aR

b), and one of them (a) is in relation R

with

some third task c (aR

c), there are only two possi-

bilities for the relation between b and c: it is either

c or bR

c. The former case (bR

c) holds when the

LCA of a and b is a descendant of the LCA of a and

c, while the latter case (bR

c) holds when the LCA of

a and c is a descendant of the LCA of a and b.

The latter case is of particular interest, and it is

true that the logical implication in question holds in

the other direction, too, even regardless of the exact

relation between a and b. By deﬁning LCA(·, ·) to be

the function that returns the node of a WF-tree that

is the LCA of its two arguments, and the binary re-

lation Descendant such that Descendant(d, a) holds

true when node d is a descendant of node a, we can

show that if nodes a and b happen to share the same

relation R respectively with a third task c, it is nec-

essarily true that their LCA is a descendant of their

respective LCAs with this third task:

Lemma 2. aR

b ∧ aR

c ∧ bR

c ∧ R

6≡ R

⇒

Descendant[LCA(a, b), LCA(a, c)].

Proof. For full proof, see the accompanying online

technical report (Nikovski and Baba, 2007).

The same stipulation about the validity of this

lemma with respect to the symmetry of R

and R

ap-

plies here, too. It follows immediately that LCA(a, b)

is a descendant of LCA(b, c), as well. We can also

prove that LCA(a, c) ≡ LCA(b, c):

Lemma 3. (aR

b ∧ aR

c ∧ bR

c ∧ R

6≡ R

) ⇒

(LCA(a, c) ≡ LCA(b, c)).

Proof. Since both LCA(a, c) and LCA(b, c) are ances-

tors to LCA(a, b) by virtue of Lemma 2, and three

leaves in the same tree can have at most two distinct

LCA nodes, then they must be the same node, i.e.

LCA(a, c) ≡ LCA(b, c).

Also note that the condition that exactly two rela-

tions hold among the three tasks in Lemmata 2 and 3

is essential: if it is the same (one) relation that holds

between each pair of tasks, nothing can be said about

the relative position in the tree or number of their re-

spective LCA nodes.

Now we are prepared to analyze the relations be-

tween a pair of tasks and all other tasks, and prove

that two tasks are children (direct descendants) of the

same node iff they are in the same respective relation

with all other tasks. This property holds for com-

pact workﬂow trees that do not contain redundant par-

ent/child nodes of the same label, and also do not con-

tain intermediate nodes of type IT ER.

Theorem 1. (∀

∃

aRc ∧ bRc) ⇔ [∃

Child(a, L) ∧

Child(b, L)].

Proof. For full proof, see the accompanying online

technical report (Nikovski and Baba, 2007).

This theorem shows that we can identify tasks that

must have the same parent node in the CWF-tree by

comparing their respective relations with every other

task — if they all match, then the two tasks share the

same parent. We will use this theorem to devise a

computationally efﬁcient process mining algorithm in

the next section. Note that the analysis will be limited

to CWF-trees without IT ER nodes, since the pres-

ence of such nodes makes impossible the application

of this theorem.

4 MINING OF WORKFLOW

TREES

In the previous section, we assumed that a CWF-tree

was given, and analyzed the properties of the rela-

tions among its tasks. In this section, we describe how

such a tree can be constructed, if all that is given is a

complete workﬂow log from the operation of the cor-

responding process. We will use a deﬁnition of log

completeness identical to that proposed by van der

Aalst et al., 2004.

Before we describe the algorithm for mining

workﬂow trees, we have to explain how all possible

pairwise relations between two tasks in a model are

determined. The binary relation AND is identical to

the relation k used in the α algorithm: aANDb ⇔

a k b. The relation SEQ is based on the relation

→ from that algorithm (a → b ⇒ aSEQb), but un-

like the latter, is transitive, and is more comprehen-

sive. From the above implication and the transitiv-

ity property aSEQb ∧ bSEQc ⇒ aSEQc, it follows

that aSEQb ∧ b → c ⇒ aSEQc, that is, the relation

SEQ is simply the transitive closure of →, and can be

found by any suitable algorithm, for example Floyd-

Warshall of complexity O(N

) (Sedgewick, 2002).

ICEIS 2008 - International Conference on Enterprise Information Systems

As described previously, aLINb ⇔ aSEQb ∨ bSEQa.

Finally, the OR relation is based on the # relation, but

is much more limited. It holds only when the SEQ

relation does not hold: aORb ⇔ a#b ∧ ¬(aLINb).

Consequently, the ﬁrst step of the mining algo-

rithm is to partition the set of all task pairs (t

i = 1, N, j = 1, N, i 6= j into three subsets of task

pairs that obey the original three relations →, k, and

#, respectively. This is done by means of establish-

ing the > relation ﬁrst by performing a single scan of

all traces in the workﬂow log, identically to the oper-

ation of the α algorithm (van der Aalst et al., 2004).

The computational complexity of this step is linear in

the length of the workﬂow log, but is independent of

the number of tasks N. Establishing →, k, and # from

> can be done in time O(N

The resulting partition of task pairs can be rep-

resented conveniently in the matrix M

whose en-

try M

i, j

contains the relation label for the pair (t

i = 1, N, j = 1, N, i 6= j. The diagonal entries M

i,i

i = 1, N are undeﬁned and excluded from considera-

tion. Note that M

is not symmetric, in general.

The second step is to build the relation matrix M

of the workﬂow tree mining algorithm, whose entries

are based on the entries M

and the deﬁnitions de-

scribed above. The order of ﬁlling in the matrix M is

strictly as listed above: AND, SEQ, LIN, and OR, and

since LIN labels overwrite SEQ labels, the end result

is a partition of the task pair set into three relation

subsets labelled with AND, OR, and LIN. Again, the

diagonal elements of M are undeﬁned and excluded

from consideration. Note that in contrast to M

, M is

symmetric. The complexity of this step is O(N

The third, and central, step of the algorithm is to

ﬁnd the difference ∆

i, j

between each distinct pair of

rows (i, j), i 6= j in the matrix M, deﬁned as ∆

i, j

∑

k=1

δ(i, j, k), for

δ(i, j, k)



1 iff i 6= k ∧ j 6= k ∧ M

i,k

6= M

j,k

0, otherwise.

(1)

If ∆

i, j

= 0 for a distinct pair of tasks (i, j), i 6= j,

this means that these two tasks have identical respec-

tive relations with respect to all remaining tasks, and

by virtue of Theorem 1 applied in the forward direc-

tion, they must have the same parent. In such case,

we can build a workﬂow subtree that has a root node

labeled with M

i, j

, and children t

and t

When more than one element ∆

i, j

= 0 (excluding

the symmetric element ∆ j, i which is also necessar-

ily zero because of the symmetry of ∆), it is not nec-

essarily always true that all corresponding nodes are

children of the same relation node. This is only true

when every pair of them (i, j) will have pairwise dis-

tance ∆

i, j

= 0 (from Theorem 1, applied in the reverse

direction.) In the general case, there might be sev-

eral sets of tasks, such that each pair of tasks t

and t

within the same set has distance ∆

i, j

= 0, but distances

between tasks from different sets are not zero. Such

distinct, non-overlapping sets of tasks can be deter-

mined easily by scanning the matrix ∆ row-wise, and

adding a task t

to an existing set only if its distance

∆

i j

to all other tasks t

in that set is zero; when it has

distance ∆

= 0 to some other task t

thas is not in

any existing set, a new set is initiated with members t

and t

Once all such sets have been found, a sub-tree is

constructed for each of them. The root of this subtree

is labeled with the relation that holds among these

tasks. Due to the semantics of WF-trees, a sub-tree

is simply a composite task that can participate in a

higher-level block just like any other atomic task. Be-

cause of this, we can create a new task label for each

sub-tree so identiﬁed. Let the set of these new com-

posite tasks be T

new

; this set complements the initial

set of atomic tasks T . The tasks t

∈ T

new

are given

successive ordinal numbers beyond N. Let also the

atomic tasks that are members of one of the cliques be

deﬁned as T

inc

; each task in T

inc

is a child of a member

of T

new

. Finally, let also a set T

act

of active tasks be

identiﬁed, and initialized at this point as T

act

:= T .

The complexity of this (third) step is O(N

), be-

cause it is dominated by the cost of computing the ma-

trix ∆. (As noted, identifying sets and building sub-

trees requires a single scan of ∆, or only O(N

).) The

next series of steps are largely similar to the one just

described, only they work on a progressively modiﬁed

active set of tasks. The newly created composite tasks

in T

new

are added to the set of active tasks T

act

, while

atomic tasks that have already been included in some

sub-tree are excluded from T

act

. New sub-trees are

again constructed on the current tasks in T

act

, and the

process is repeated until only one task remains in T

act

— the root of the entire WFT. For a detailed descrip-

tion of these steps, see (Nikovski and Baba, 2007).

The overall complexity of this series of steps is again

O(N

), because new rows and columns of the matri-

ces M and ∆ are introduced only for new composite

tasks, and there can be at most N −1 such tasks. Each

new row or column has O(N) elements, and the com-

putation of each element takes O(N).

The last step of the algorithm is to re-order the

children of all LIN nodes, so that the SEQ relation

among them holds, and re-label those nodes with the

label SEQ. This completes the construction of the

workﬂow tree. Since, by construction, each com-

posite node has at least two children, this workﬂow

tree is also compact. The complexity of this step

is O(N

logN), since the induced tree has at most

WORKFLOW TREES FOR REPRESENTATION AND MINING OF IMPLICITLY CONCURRENT BUSINESS

PROCESSES

N − 1 internal nodes, each of which has O(N) chil-

dren which are sortable in O(N logN) time. Based on

the complexity of each step, the overall computational

complexity of the algorithm is O(N

5 CONCLUSIONS

We have described a representation of business pro-

cesses called workﬂow trees that is intuitive and

matches the hierarchical organization of most busi-

ness processes used in practice. While similar to

other business process representations used in the

past, workﬂow trees have precise semantics and prop-

erties which derive directly from their tree-like repre-

sentation. These properties can be leveraged to devise

a computationally efﬁcient process mining algorithm

that can recover business process models with concur-

rent tasks that have not been speciﬁed as such explic-

itly in workﬂow logs. The algorithm operates by an-

alyzing and comparing the mutual relations between

pairs of tasks, suitably organized in matrices, and this

determines its favorable computational complexity —

cubic in the number of process tasks.

This computational efﬁciency is achieved at the

expense of a slight sacriﬁce in the representational

power of workﬂow trees in comparison to other for-

malisms, such as workﬂow nets (van der Aalst et al.,

2004). The set of process models that can be repre-

sented by workﬂow trees is a strict subset of the set

of models that can be represented by workﬂow nets

— there exist some processes that can be represented

by workﬂow nets, but not by workﬂow trees, most no-

tably some processes with complex concurrency and

mixed synchronization.

A more serious limitation of the current version of

the mining algorithm is that it cannot recover models

with looped execution. While such models are eas-

ily represented by workﬂow trees, using several pos-

sible iterative constructs, the mining algorithm pro-

posed in this paper relies on the property of induced

trees that each of their internal nodes must have at

least two children. This effectively excludes iterative

constructs from the set of blocks that can be used for

building induced models.

However, this is not a principled restriction — in

fact, the presence of looped execution can easily be

detected as a by-product of computing the transitive

closure SEQ of the → relation. If there exists a task

a such that aSEQa, then the process must contain a

loop. However, identifying how many loops exist,

where the corresponding IT ER constructs should be

positioned in a workﬂow tree, and how the tree should

be mined in the presence of such constructs, is still an

open problem to be addressed by future work.

REFERENCES

Cook, J. E. and Wolf, A. L. (1998a). Discovering models

of software processes from event-based data. ACM

Trans. Softw. Eng. Methodol., 7(3):215–249.

Cook, J. E. and Wolf, A. L. (1998b). Event-based detection

of concurrency. In SIGSOFT ’98/FSE-6: Proceed-

ings of the 6th ACM SIGSOFT international sympo-

sium on Foundations of software engineering, pages

35–45, New York, NY, USA. ACM Press.

de Medeiros, A., van Dongen, B., van der Aalst, W., and

Weijters, A. (2004). Process mining: Extending the α-

algorithm to mine short loops. BETA Working Paper

Series, WP 113, Eindhoven University of Technology,

Eindhoven.

List, B. and Korherr, B. (2006). An evaluation of conceptual

business process modelling languages. In SAC ’06:

Proceedings of the 2006 ACM symposium on Applied

computing, pages 1532–1539, New York, NY, USA.

ACM Press.

Nikovski, D. and Baba, A. (2007). Workﬂow trees

for representation and mining of implicitly con-

current business processes. Technical Report

TR2007-072, Mitsubishi Electric Research Labs,

www.merl.com/publications/TR2007-072.

Schimm, G. (2004). Mining exact models of concurrent

workﬂows. Comput. Ind., 53(3):265–281.

Sedgewick, R. (2002). Algorithms in C. Addison-Wesley

Longman Publishing Co., Inc., Boston, MA, USA.

Silva, R., Zhang, J., and Shanahan, J. G. (2005). Probabilis-

tic workﬂow mining. In KDD ’05: Proceeding of the

eleventh ACM SIGKDD international conference on

Knowledge discovery in data mining, pages 275–284,

New York, NY, USA. ACM Press.

van der Aalst, W., Weijters, T., and Maruster, L. (2004).

Workﬂow mining: Discovering process models from

event logs. IEEE Transactions on Knowledge and

Data Engineering, 16(9):1128–1142.

van der Aalst, W. M. P. and van Hee, K. M. (2002). Work-

ﬂow Management: Models, Methods, and Systems.

MIT Press.

van der Aalst, W. M. P. and Weijters, A. J. M. M. (2004).

Process mining: a research agenda. Comput. Ind.,

53(3):231–244.

ICEIS 2008 - International Conference on Enterprise Information Systems