A MATHEMATICAL FORMULATION OF A MODEL FOR

LANDFORM ATTRIBUTES REPRESENTATION FOR

APPLICATION IN DISTRIBUTED SYSTEMS

Leacir Nogueira Bastos,

Rossini Pena Abrantes and

Brauliro Gonçalves Leal

Informatics Department, Viçosa Federal University, PH Rolfs Avenue, Viçosa, Brazil

INTEC Group Researcher, Brazil

Keywords: Mathematical Modeling of Landform Attributes, Distributed Processing, Internet, Nonlinear Regression,

Polynomial Estimation.

Abstract: This study presents a methodology based on nonlinear regression for landform attributes representation. The

equations to estimate the parameters of a two-dimensional polynomial are shown and, for testing the

methodology, it was used the data from landform attributes of the state of Minas Gerais (Brazil) obtained by

the Digital Elevation Model (DEM) in GTOPO30 project. They form a regular grid, with spacing of

approximately 900m. The presented methodology can be used to minimize time of sending landform

attributes information through network, to minimize space by storing the parameters of the estimated

polynomial, and to make possible the process distribution of the polynomial coefficients calculations to

different CPUs over internet network.

1 INTRODUCTION

The increased efficiency and reliability of computer

networks (Fowler, 2005), as well as the

popularization of the Internet, have generated new

opportunities for applications development. Now,

with the growing number of connected computers in

the Internet (Zakon, 2006), it is possible to distribute

applications, using communication infrastructure,

without great efficiency problems. An application

that has access to the resources of the Internet can

use the services as HTTP, SMTP, POP3, FTP, for

updating through remote servers (Tanenbaum,

2002).

In Geo-informatics, there is an area called

Numerical Model of Surface that treats the

mathematical representation of landforms (INPE,

2001). One of the numerical models most common

used is the Regular Grid Model whose function is to

generate a grid starting from a group of elevation,

longitude and latitude points as in Figure 1.

Figure 1: Regular Grid Model.

This grid can be generated by point interpolation

for a polynomial regression model that adjusts a

two-dimensional polynomial which best represents

the landform attributes of an area (Burrough, 1986)

(Ervin and Hasbrouck, 2001). The regression

analysis is a statistical instrument often used in

science. Its common use is to make possible the

description of a phenomenon by means of a

mathematical model (equation), based on a data

sample. Graphically, it is equivalent to identify the

curve or mathematical surface that best adjusts to the

points in a dispersion diagram. The mathematical

models of regression are based in three statistical

assumptions: a) the relationship among the

184

Nogueira Bastos L., Pena Abrantes R. and Gonçalves Leal B. (2008).

A MATHEMATICAL FORMULATION OF A MODEL FOR LANDFORM ATTRIBUTES REPRESENTATION FOR APPLICATION IN DISTRIBUTED

SYSTEMS.

In Proceedings of the Fourth International Conference on Web Information Systems and Technologies, pages 184-189

DOI: 10.5220/0001527901840189

 SciTePress

dependent and independent variables is deterministic

instead of stochastic; b) the error measurements are

random, following the normal distribution, average

zero and constant variance; and c) the explanatory

variables don't show correlation among themselves

(Seber and Wild, 2005). This technique of landform

attributes representation has some advantages over

other techniques, basically by representing the

landform attributes by mathematical equations

instead of images, latitude, longitude and elevation

coordinates, or map of elevation levels. One of the

advantages is the significant reduction of the amount

of necessary information to represent the landform

attributes of a certain area, since, with the regression

technique, the landform attributes of an entire area

can just be represented through the coefficients of

two-dimensional polynomial. By the polynomial

representation it is possible to generate images with

different resolution levels because, with a

polynomial function, we may generate as many

points as needed. Besides these advantages, there is

a possibility to apply, on the polynomial, several

mathematical operations, such as finding the

maximal and minimal point, derivation, etc.

However, the technique of polynomial regression

has some disadvantages too, since the complexity

and the computational power demanded in obtaining

such polynomial is very high and sometimes

impractical.

For that reason the objective of this article is to

present a methodology designed to make possible

the distribution of the necessary processing to

compute a two-dimensional polynomial that

represents the landform attributes of an area and, as

an example, we use the area of the state of Minas

Gerais, in Brazil, located in the Southeastern area of

the country. Some estimative calculations, presented

in this article, show that the necessary time of

centralized processing to estimate such a polynomial

is prohibitive, being in order of dozens of

uninterrupted years of processing.

2 MATHEMATICAL METHOD

In this work we present a methodology for landform

attributes representation using the method of

nonlinear regression to adjust a two-dimensional

polynomial. The regression analysis is a statistical

instrument very used in science. Its frequent use is

due to the fact of making possible the description of

phenomena through mathematical models from a

data sample. Graphically, it is equal to identify the

curve or mathematical surface that best adjusts to the

points in a dispersion diagram. The mathematical

models of regression are based on three statistical

facts: a) the relationship among the dependent and

independent variables is deterministic instead of

stochastic; b) the errors are random with normal

distribution, average zero and constant variance; and

c) the explanatory variables don't present correlation

among themselves (Seber and Wild, 2005).

When a mathematical model of regression is

used, the most used method of estimating the

parameters is the Least Squares Method which

consists of estimating a function to represent a group

of points, minimizing the square of the deviations

(Nobel and Daniel, 1986). Considering a group of

geographic coordinates (x, y, z), representing

longitude, latitude, and elevation of each point,

respectively, we may take an estimate elevation

function

),(

yxfz

of these points. A

polynomial of degree r in x and degree s in y can be

given, according to Equation 1, and the estimated

error ε

is given by Equation 2 where 0 ≤ i ≤ m and

0 ≤ j ≤ n.

∑∑

iklji

yxayxfz

),(

(1)

ijijij

−

(2)

The coefficients a

(k = 0, 1, ..., r, l = 0, 1, ..., s)

that minimize the errors of the estimated function

f (x, y) can be obtained by solving Equation 3 for c =

0, 1, ..., r and d = 0, 1, ..., s.

∂

(3)

where

∑∑∑∑

====

−==

jiij

)

(

εξ

(4)

and

longitude i of DEM column, for 1 ≤ i ≤ k

latitude j of DEM line, for 1 ≤ j ≤ l,

zij elevation of point (xi, yi)

r polynomial degree in x,

s polynomial degree in y,

akl coefficients which minimize the error of the

estimated function f (x, y)

A MATHEMATICAL FORMULATION OF A MODEL FOR LANDFORM ATTRIBUTES REPRESENTATION FOR

APPLICATION IN DISTRIBUTED SYSTEMS

185

By solving Equation 3, we get Equation 5 through

Equation 12. By solving Equation 1 for a particular

case of r = s = 2, we get Equation 13. By solving

Equation 12 for the particular case of r = s = 2, we

get the matrix system of equations in Figure 2,

represented by AX=B where the matrix A is formed

by x

terms, matrix X is formed by a

, estimated

coefficients as the system solution, and matrix B as

the independents terms b

These terms, x

and b

, are

shown as Equation 14 and Equation 15, respectively,

as a general solution for any r and s of Equation 12.

The estimated time to calculate the coefficients of

Equation 14 and Equation 15 varies with degree of

the polynomial, and may range from 28 sec for r = s

= 2 to 45.9 years for r = s = 500 as show in Figure 3.

The estimated error decreases with the increasing of

the polynomial degree, as shown in Figure 4.

Equation 14 and Equation 15 can be processed in an

independent way, fundamental characteristic of

distributed processing in different CPUs over a

network system.

3 RESULTS

To validate the present methodology and derived

equations, they will be applied to represent the

landform attributes of an area of the state of Minas

Gerais (Brazil). The data source of the chosen area,

comes from a Digital Elevation Model (DEM) called

GTOPO30 project (GTOPO30, 2006), in the form of

a regular matrix with 1,043 lines and 1,343 columns,

with spacing approximately 900m in the

geographical coordinates.

Using the data source form the GTOPO30

(GTOPO30, 2006) project, the statistical analyses of

the elevations of the state of Minas Gerais indicate a

dispersion from 1m (meter) to 2,863m (meter). The

distribution of these points, in 200m by 200m

intervals, is presented in Table 1.

yxyf

∑∑

),(

(5)

⎟

⎠

⎞

⎜

⎝

⎛

−=

∑∑

klijij

yxaz

(6)

klij

yxaz

∑∑

==00

(7)

00 00

∑∑ ∑∑

== ==

⎟

⎠

⎞

⎜

⎝

⎛

−=

klij

yxaZ

(8)

∑∑ ∑∑

== ==

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−=

∂

iklij

yxyxaz

00 00

(9)

00 00

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

∑∑ ∑∑

== ==

iklij

yxyxaz

(10)

∑∑∑∑∑∑

======

iij

ikl

yxzyxa

000000

(11)

00 00

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

∑∑ ∑∑

== ==

ikl

iij

yxayxz

(12)

),( yxayxayxayxayxayxayxayxayxayxZ

jiij

++++++++=

)

(13)

WEBIST 2008 - International Conference on Web Information Systems and Technologies

186

{} {} {} {} {} {} {} {} {}

{}

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

∑∑

∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑∑

==================

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0,0

8,8

7,8

6,8

5,8

4,8

3,8

2,8

1,8

8,7

7,7

6,7

5,7

4,7

3,7

2,7

1,7

0,7

8,6

7,6

6,6

5,6

4,6

3,6

2,6

1,6

0,6

8,5

7,5

6,5

5,5

4,5

3,5

2,5

1,5

0,5

8,4

7,4

6,4

5,4

4,4

3,4

2,4

1,4

0,4

8,3

7,3

6,3

5,3

4,3

3,3

2,3

1,3

0,3

8,2

7,2

6,2

5,2

4,2

3,2

2,2

1,2

0,2

8,1

7,1

6,1

5,1

4,1

3,1

2,1

1,1

0,1

8,0

7,0

6,0

5,0

4,0

3,0

2,0

1,0

0,0

jiij

yxZ

yxyxyxyxyxyxyxyxyx

yxyxyxyxyxy

xyxyxyx

yxyxyxyxyxyxyxyxyx

Figure 2: Matrix system generated from solving Equation 12 considering a simple case of r = s = 2.

∑∑

++++++

rcrl

sdivcsdivl

ilc

yxx

)1(mod)1(mod)1()1(

(14)

∑∑

sdivl

iijl

yxzb

)1(mod)1(

(15)

Table 1: Classes of elevations and relative percentage of

the points, in each class, considering the DEM data of the

State of Minas Gerais. The classes are intervals of 200m,

from 0 to 2,900m.

Classes of

elevation (m)

Number of

points

Percentage

of point in a

class (%)

Accumulated

percentage of

points at classes

(%)

0001 – 200 5,055 0,69986 0.6999

0201 – 400 48,866 6.76538 7.4652

0401 – 600 127,776 17.6903 25.1555

0601 – 800 249,762 34.57899 59.7345

0801 – 1000 226,481 31.3558 91.0903

1001 – 1200 36,246 5.01818 96.1085

1201 – 1400 22,334 3.09209 99.2006

1401 – 1600 4,482 0.62053 99.8211

1601 – 1800 811 0.11228 99.9334

1801 –2000 331 0.04582 99.9792

2001 – 2200 99 0.0137 99.9929

2201 – 2400 24 0.00333 99.9963

2401 – 2600 16 0.00221 99.9985

2601 – 2800 10 0.00139 99.9999

2801 – 3000 1 0.00014 100.0000

722,294 100.00000 –

The DEM with 1,400,749 points has only

722,294 points into the state of Minas Gerais, the

others points are outside the state area. Using all the

points representing the landform attributes of the

state and by using Equations 14 and 15 we estimate

the polynomial coefficients for representing the

landform attributes of the state of Minas Gerais.

Since the time to estimate such a polynomial in high

degree needs great computer power and a long time

of processing, we compute only a small sample, for r

= s = 2, 3, 10 and 20. The processing was done by a

usual PC machine with Intel Pentium 4 processor,

running Windows XP.

The processing times in seconds t(s) and the

regression coefficient R

of the adjusted polynomial

of degrees r in x and s in y, with r = s, are presented

in Table 2.

Table 2: Processing times in seconds t(s) and R2 for the

adjusted polynomial of degree r in x and degree s in y,

with r = s.

r = s t(s) R

2 28 0.41547

3 86 0.47168

10 4,746 0.60450

20 62,675 0.64767

A MATHEMATICAL FORMULATION OF A MODEL FOR LANDFORM ATTRIBUTES REPRESENTATION FOR

APPLICATION IN DISTRIBUTED SYSTEMS

187

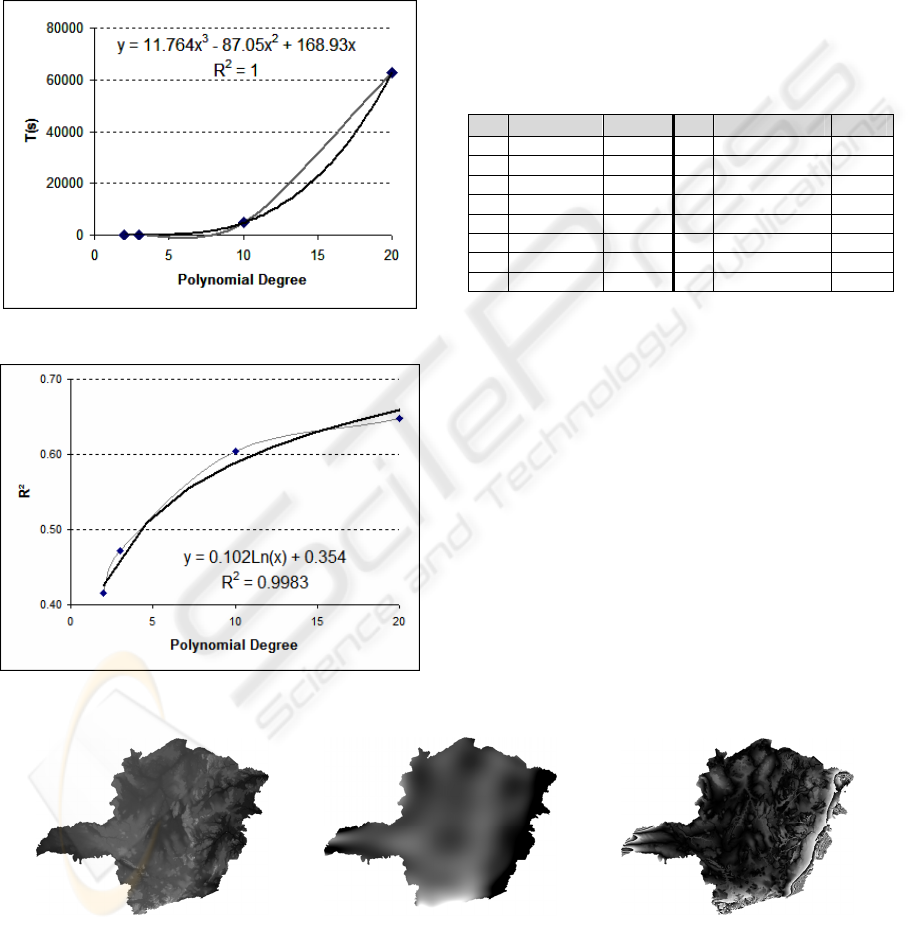
With the values from Table 2 and by using

polynomial regression, we get Equation 16 and

Equation 17 that estimate the time t(s) and R

respectively, with r = s.

sssst 93.16805.87764.11)(

+−=

= 1.0

(16)

354.0)ln(102.0)(

+= ssR

= 0.9983

(17)

Figure 3: Processing time estimative.

Figure 4: Estimated error.

From Equation 16 and Equation 17 we simulated

the time processing in second t(s), and the

coefficient of regression R

, to adjusted a

polynomial to represent the landform attributes for r

= s, varying from 30 to 500 degree, as shown on

Table 3. As an example, for r = s = 500, using the

PC machine previously described, the polynomial

representing the state of Minas Gerais, will be

adjusted with R

=0.988 and will need 45.9 years to

generate the coefficients.

Table 3: Processing time in seconds t(s) and R

for the

polynomial of degree r in x and s in y, r = s, from 30 to

500 degrees.

r=s t(s) R

30 244,351 0.70102 225 129,630,416 0.9065

40 620,373 0.73037 250 178,414,108 0.9173

60 2,237,780 0.77172 300 309,844,179 0.9359

80 5,479,562 0.80107 350 493,777,001 0.9516

90 7,886,055 0.81308 375 608,189,130 0.9587

100 10,910,393 0.82383 400 739,035,572 0.9652

150 37,770,215 0.86518 450 1,054,442,894 0.9772

200 90,663,786 0.89453 500 1,448,821,965 0.988

Using the DEM data source, an elevation map

was generated in gray tones, Figure 5-a, where can

be observed that the state of Minas Gerais has a

heavily uneven topography. With the coefficients of

the adjusted polynomial of degrees r = s = 20, the

elevation map was also generated, Figure 5-b. In

Figure 5-c, we show the relative errors computed

using the source data (DEM) and the estimated data

(polynomial).

Since we used only points that represent the

landform attributes of the state of Minas Gerais, the

bordering areas suffered heavy alterations,

generating non existent elevations. This anomaly can

be corrected by taking points that cross the limits of

the real area, for estimation of the polynomial

parameters.

Figure 5: Elevation map of Minas Gerais state generated by: (a) DEM of GTOPO project, (b) estimated polynomial with r =

s = 20 that represents the DEM and (c) the relative errors form the data source and the estimated data.

(a) (b) (c)

WEBIST 2008 - International Conference on Web Information Systems and Technologies

188

The elevations of DEM and the elevations

estimated by the polynomial of degrees r = s = 20

are displayed in classes in Table 4. By analysis of

those data we may verify that the classes are

comparable, although the adjusted polynomial

generates some values above the maximum and

below the minimum real elevations. It is believed

that with larger r and s, we can get better values of

and that will improve the accuracy of the

polynomial parameters.

4 CONCLUSIONS

Table 4: Elevation classes from the DEM source and

estimated polynomial for r = s = 20.

Elevation

Classes(m)

Points from

DEM (source

data)

Points from

estimated

polynomial

0 - 200 5,055 78,725

0201 - 400 48,866 42,757

0401 - 600 127,776 119,401

0601 - 800 249,762 222,355

0801 - 1000 226,481 158,256

1001 – 1200 51,055 47,817

1201 – 1400 22,334 16,348

1401 – 1600 4,482 9,823

1601 – 1800 811 6,443

1801 -2000 331 4,687

2001 – 2200 99 3,548

2201 – 2400 24 2,683

> 2400 27 9,451

Minimum Elevation 1 -4,374

Maximum Elevation 2,863 5,606

The adjusted polynomial of degree 20 in x and y has

441 coefficients. If we use the type float to store

them, it will be necessary 1,764 KB of storage. The

DEM, on the other hand, with 722,294 points,

requires at least 2 bytes to indicate the elevation of

each point, being necessary the total of 1,444 MB to

store it. The adjusted polynomial needs about

0.1221% of space used by the DEM. From the

results, it is verified that is possible to represent,

satisfactorily, the landform attributes of an area by a

high degree polynomial and the representation has

the advantage of smaller space. Additionally, the

functional representation of the landform attributes

allows larger efficiency, in time and space when

sending this information through networks.

Efficiency in time is real since, instead of sending an

image with millions of points, the coefficients of a

mathematical function are sent. Efficiency in space

is also obtained since, instead of storing the DEM,

we may store the coefficients that represent it. In this

methodology, larger polynomial degree, better is the

solution. For this work, a polynomial of degree 20

was used, however with a polynomial of degree 200

or larger, the results, statistically, would be better.

The presented methodology also has the advantage

of being easily adaptable for distributed processing.

REFERENCES

Burrough, P. A., 1986. Principles of Geographical

Information Systems for Land Resources Assessment.

Clarendon Press, Oxford, England.

Ervin, S. M., Hasbrouck, H. H., 2001. Landscape

Modeling: Digital Techniques for Landscape

Visualization. McGraw-Hill Professional Publishing.

Fowler, D., 2005. A Supercomputer in Every Home?.

NetNews.

INPE, 2001. Introdução à Ciência da GeoInformação.

INPE. São José dos Campos, SP, Brazil.

Noble, B., Daniel, J. W., 1986. Álgebra Linear Aplicada.

Prentice/Hall do Brasil, Rio de Janeiro, Brazil.

Seber, G. A. F., Wild C. J., 2005. Nonlinear Regression

John Wiley, New York, N.Y IEEE.

Tanenbaum, A. S., 2002. Computer Networks. 4th Edition,

Prentice Hall, Upper Saddle River, N.J..

U.S. Geological Survey GTOPO30, 2006. [Internet].

Available from: http://edc.usgs.gov/products/

elevation/gtopo30/gtopo30.html.

Zakon, R. H., 2006. Hobbes' Internet Timeline. [Internet].

Available from: http://www.zakon.org/robert/internet/

timeline/#Growth.

A MATHEMATICAL FORMULATION OF A MODEL FOR LANDFORM ATTRIBUTES REPRESENTATION FOR

APPLICATION IN DISTRIBUTED SYSTEMS

189