A UNIFYING POINT OF VIEW IN THE PROBLEM OF PIO
Pilot In-the-loop Oscillations
Vladimir R˘asvan, Daniela Danciu and Dan Popescu
Department of Automatic Control, University of Craiova
13 A. I. Cuza Str., RO-200585 Craiova, Romania
Keywords:
Oscillations, Feedback structure, Robustness.
Abstract:
The paper starts from the problem of PIO (Pilot-In-the-loop Oscillations), a major problem in aircraft handling
and control, where the idea of the feedback as hidden technology is basic. The real phenomenon called PIO
is modeled by a feedback structure where the pilot acts as one of the components of the loop and has to be
modeled accordingly. PIO are in fact self-sustained oscillations and usually are divided into three convenient
categories that are based on the nature of the pilot and vehicle dynamics behavior models and analysis needed
for their explanation. Category I PIO are essentially linear while Category II PIO are quasi-linear and typically
associated with rate limiting. Category III PIO are fully nonlinear and non-stationary. Since PIO II are mostly
tackled via various robustness approaches starting from linear models, the paper strives for a unifying approach
which is illustrated accordingly.
1 BASICS AND PROBLEM
STATEMENT
According to the standard terminology of the field,
PIO (Pilot Induced Oscillations, Pilot In-the-loop Os-
cillations, Pilot InvolvedOscillations) are sustained or
uncontrollable oscillations resulting from the effort of
the pilot to control the aircraft, hence they can be con-
sidered as a closed loop destabilization of the aircraft-
pilot loop (Anon., 2000),(McRuer et al., 1996). Even
from this remarkably short definition it appears that
the real phenomenon called PIO can be modeled by a
feedback structure where the pilot acts as one of the
components of the loop and has to be modeled ac-
cordingly. As mentioned in (McRuer et al., 1996) the
study of the aeronautical history reveals a remarkably
diverse set of severe PIOs as exemplified by the list-
ings of “famous PIOs” (McRuer, 1994),(Klyde et al.,
1995).
The feedback control character of PIOs was rec-
ognized almost from the outset because the aircraft
left alone did not exhibit such oscillations. Once rec-
ognized as oscillations within a feedback system con-
text, mathematical models were developed and used
to describe the pilot’s dynamic actions as a controller
and active participant in PIOs.
A. Detailed analytical studies of past PIO inci-
dents (see e.g. the references from (McRuer et al.,
1996)) relied on pilot behavioral models and closed
loop analysis procedures to understand and rational-
ize phenomena. Moreover in some cases pilot vehicle
behavioral models were applied to design and assess
changes to the effective vehicle to alleviate the PIO
potential. Based on these results it is useful to divide
PIOs into categories that reflect the analytical and pi-
lot modeling tools. There were identified three cate-
gories of PIO as follows:
- Category I - Essentially Linear Pilot Vehicle Sys-
tem Oscillations: the element characteristics are
essentially linear and the pilot behavior is linear
(except, possibly, for simple gain shaping in se-
ries with the pilot).
- Category II - Quasi-Linear Pilot Vehicle Systems
with Series Rate or Position Limiting. Rate limit-
ing, either as a series element or as a rate limited
surface actuator modifies the Category I situation
by adding what is called (non-rigorously) an am-
plitude dependent lag and by setting the limit cy-
cle magnitude.
- Category III - Essentially Non-Linear Pilot Vehi-
cle System Oscillations with transitions: they fun-
damentally depend on nonlinear transitions in ei-
ther the effective control element or in the pilot
behavioral dynamics.
B. Most of the available information shows that
mainly PIO I and PIO II were considered and ana-
lyzed due to the complexity of PIO III which never-
200
R
ˇ
asvan V., Danciu D. and Popescu D. (2008).
A UNIFYING POINT OF VIEW IN THE PROBLEM OF PIO - Pilot In-the-loop Oscillations.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 200-204
DOI: 10.5220/0001505602000204
Copyright
c
 SciTePress

theless have been recognized as quite rare and arising
from PIO I and PIO II; consequently a consensus has
been established in the PIO community that PIO III
proneness may be blocked by blocking PIO I and PIO
II proneness. With respect to this several PIO I and
PIO II criteria have been elaborated in USA and in
Europe. These criteria are viewed as sufficient condi-
tions ensuring that the feedback system pilot-aircraft
is PIO free. Most of them are obtained in the linear
case i.e. for PIO I. Here several remarks are neces-
sary. It is a trivial fact that for linear systems there
exist necessary and sufficient conditions for stabil-
ity what means also absence of self sustained oscil-
lations. The PIO criteria are only sufficient condi-
tions but they are conceived as to ensure some kind
of robustness with respect to system’s uncertainties.
Indeed the presence of uncertainties is quite obvious.
There are first the uncertainties of aircraft modeling
- aerodynamic forces and coefficients depending of
the flight envelope parameters - but also those of pilot
modeling which depend on several modeling assump-
tions.
On the other hand, as already mentioned, PIO II
are associated to quasi-linear models where rate and
position limiters are active. The limiters are modeled
as structures containing saturation nonlinear func-
tions; the quite recent models which are based on In-
tegral Quadratic Constraints (Megretski and Rantzer,
1997),(Megretski, 1997) take into account the sim-
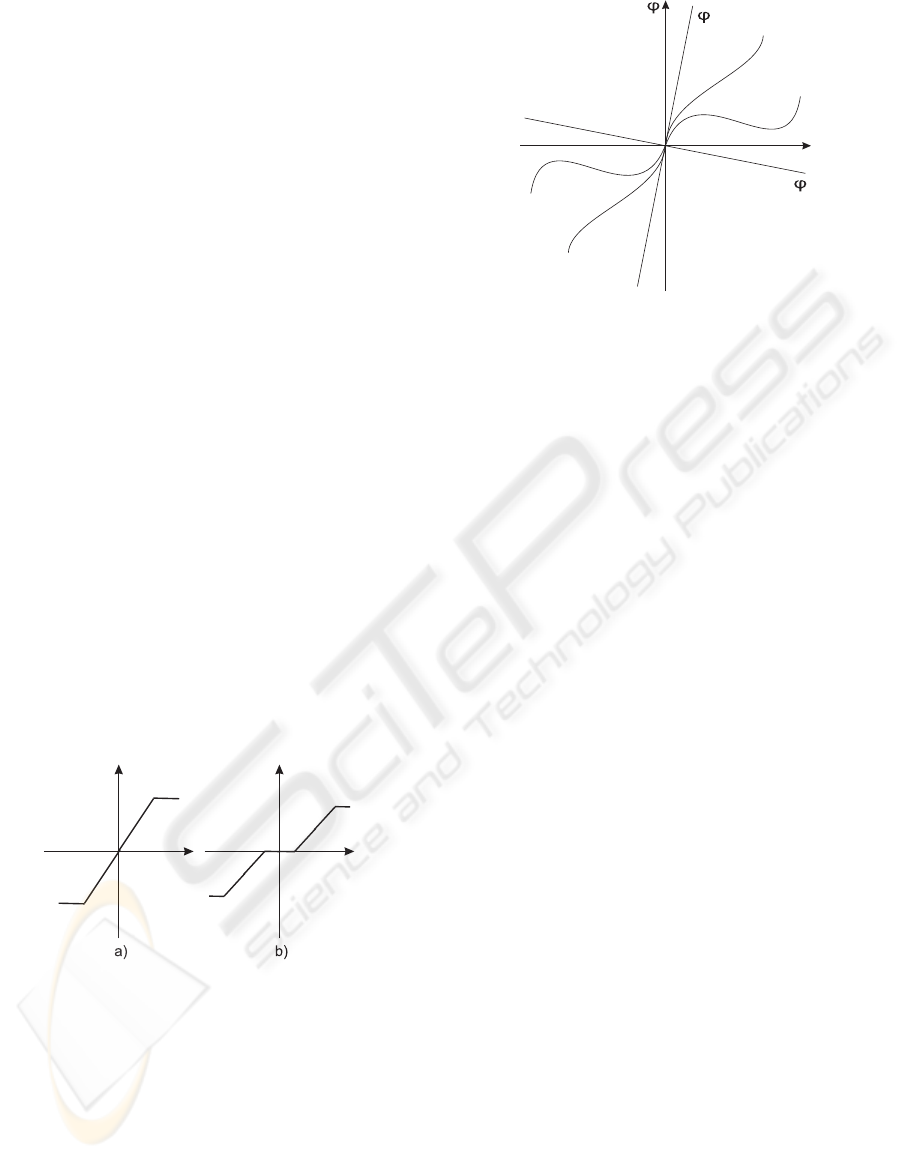
plest remark that the saturation nonlinearity (fig. 1)
may be “embedded” in the larger class of the sector
restricted nonlinearities (fig. 2)
Figure 1: Saturation nonlinearities.
As known, the properties of the sector re-
stricted nonlinearities may be expressed under the
form of some quadratic constraints - see (Megret-
ski and Rantzer, 1997) but also the pioneering pa-
per (Yakubovich, 1967) as well as the monograph
(R˘asvan, 1975). This embedding of the nonlinear
function in a larger class speaks about allowing some
uncertainty concerning the nonlinearity; additionally,
if the stability results are valid uniformly for the entire
class of non linearities, some robustness is ensured.
Consequently, it is not by chance that an impor-
-
-
s
Figure 2: Sector restricted nonlinearity.
tant class of methods associated to PIO II originate
from robustness approaches. Moreover, one can find
there such standard methods of the absolute stability
as the Liapunov function of the form “quadratic form
of the state variables plus integral of the nonlinear
function” or the Popov frequency domain inequality
(Anon., 2000).
The above considerations show that it is not with-
out interest to discuss PIO I and PIO II within a uni-
fied context of robustness in the sense that the robust-
ness restrictions introduced in the totally linear case
(PIO I) should be taken into account in the quasi-
linear (PIO II) case. As an at-hand example, the fre-
quency domain restrictions of the Neal-Smith crite-
rion (Neal and Smith, 1971) should be reflected in a
Popov like frequency domain inequality.
The present paper will demonstrate and motivate
the above sketched approach and what remains is or-
ganized as follows. Firstly the basic feedback struc-
ture is presented in the context of fully linear models
accounting for PIO I. It is then shown how rate lim-
iters occur in the loop - the PIO II onset - and the new
structure of a feedback nonlinear system with a sector
restricted nonlinearity. The linear subsystem is then
identified and a frequency domain inequality is then
formulated. This inequality has to be valid for the fre-
quency domain characteristic as resulting from a PIO
I criterion; if this holds we may say that PIO I gives
“some insurance” for PIO II. Next a specific case will
be discussed to illustrate the principle and conclusions
together with suggestions for future research and tests
are given.
2 ROBUSTNESS VERSUS
ABSOLUTE STABILITY
The analysis of the models of (Anon., 2000),(McRuer
et al., 1996),(Klyde et al., 1996),(Klyde and Mitchell,
A UNIFYING POINT OF VIEW IN THE PROBLEM OF PIO - Pilot In-the-loop Oscillations
201

H
c
(s)
r
+
-
y
H
a
(s)
Figure 3: Basic linear feedback structure.
2005) which deal with longitudinal PIO will suggest
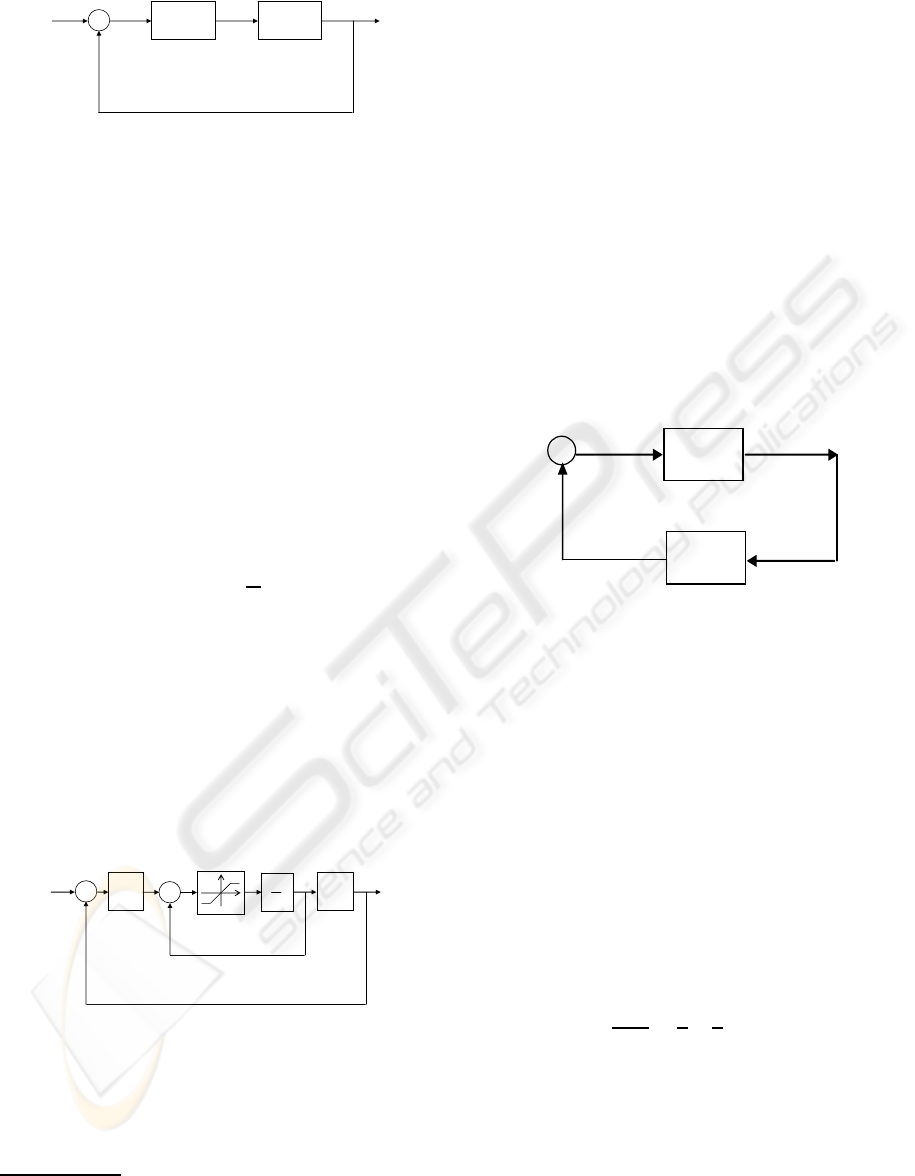
the general feedback structure of fig. 3.
We denoted there by H
a
(s) the transfer function of
the “uncontrolled plant” which might be some longi-
tudinal or lateral motion of the aircraft; by H
c
(s) we
denoted the “controller” which in this man/machine
system might be some pilot model (for instance the
so-called synchronous pilot is just a gain - see (Klyde
et al., 1996)).
Some remarks are necessary from this very be-
ginning. Since various assumptions on pilot behav-
ior may require pole/zero cancelation, only LHP (left
hand plane) i.e. stable poles and zeros may be can-
celed, otherwise uncontrollable unstable modes will
appear. This is particularly true for the so-called
crossover model where we have
H
c
(s)H
a
(s) ≡
K
s
e
−τs
(1)
and this clearly implies pole/zero cancelation. Since
it is well known that modern fighters become unstable
for high speed points of the flight envelope, they are
made stable by additional stabilizing feedback - the
SAS (Stability Augmentation System). Equality (1)
avoids unstable pole/zero cancelation only if the SAS
is active
1
.
If the limiters are to be considered, the system of
fig. 3 will become a standard feedback control struc-
ture with a nonlinear (saturated) actuator (fig. 4)
H
c
(s)
r
-
y
H
a
(s)
1
s
-
H
H
a
u
c
u
u
.
Figure 4: Feedback structure with rate limiter.
In order to obtain the standard structure of the ab-
solute stability problem, we consider the state real-
izations of the two proper rational transfer functions
H
a
(s) and H
c
(s) embedded in the structure of fig. 4
1
This explains also in some way the X-15 landing flare
PIO evoked in (Klyde et al., 1996) since it is mentioned
there that the “pitch damper was off”, the pitch damper be-
ing the SAS of the channel
˙x
a
= Ax
a
+ bu , y = c
T
x
a
+ h
0
u
˙u = ϕ(ε
a
) , ε
a
= u
c
− u
˙x
c
= A
c
x
c
+ b
c
ε , ε = r(t) − y
u
c
= f
T
c
x
c
+ h
c
ε
(2)
which becomes
˙x
a
= Ax
a
+ bu
˙x
c
= −b
c
c
T
x
a
+ A
c
x
c
− h
0
b
c
u+ b
c
r(t)
˙u = ϕ(σ)
σ = −h
c
c
T
x
a
+ f
T
c
x
c
− (1 + h
c
h
0
)u+ h
c
r(t)
(3)
For r(t) ≡ 0 what means the system is considered in
deviations with respect to some steady state (equilib-
rium) the feedback structure of fig. 5 is obtained
L
N
u
V
-
Figure 5: Absolute stability feedback structure.
The linear subsystem is described by the controlled
system of ordinary differential equations with linear
output
˙x
a
= Ax
a
+ bu
˙x
c
= −b
c
c
T
x
a
+ A
c
x
c
− h
0
b
c
u
˙u = −µ(t)
σ = −h
c
c
T
x
a
+ f
T
c
x
c
− (1 + h
c
h
0
)u
(4)
in feedback connection with the nonlinear static block
µ = −ϕ(σ) (5)
The transfer function of (4) is
H(s) =
˜
σ(s)
˜µ(s)
=
1
s
+
1
s
H
c
(s)H
a
(s) (6)
and the characteristic equation clearly has a zero root.
This might be the simplest critical case of the absolute
stability, but if (1) holds the case corresponds to the
non-simple zero root - the most special critical case,
that was studied separately of the other ones, due to its
specific problems; moreover the presence of the delay
in (1) will complicate the approach (R˘asvan, 1975);
we give here an adaptation of Theorems 6.1 and 7.2
of (R˘asvan, 1975)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
202

Theorem 1. Consider the system of fig. 5 where the
linear subsystem has its transfer function of the form
(6) with H
c
(s)H
a
(s) being a meromorphic function
- ratio of quasi-polynomials; the denominator has a
simple zero root and all other roots with negative real
parts. The nonlinear function ϕ is subject to the fol-
lowing conditions
σϕ(σ) > 0 (σ 6= 0) , ϕ(0) = 0 ,
lim
σ→±∞
Z
σ
0
ϕ(λ)dλ = ∞
(7)
Assume that
1− lim
s→0
+
H
c
(s)H
a
(s) > 0 (8)
and also that the frequency domain inequality
1+ Re H
c
(ıω)H
a
(ıω) > 0 (9)
holds for all ω > 0. Then the system has the absolute
stability property.
3 A SIMPLE APPLICATION:
ROBUSTNESS OF THE NEAL -
SMITH CRITERION
We shall consider here one of the cases of (Klyde and
Mitchell, 2005), the so-called crossover PVS (Pilot
Vehicle System) model with H
c
(s)H
a
(s) as in (1), the
parameters being chosen to satisfy
- crossover frequency ω
c
= 1.4 rad/sec,
- neutral stability frequency ω
0
= 1.73 rad/sec,
- phase margin Φ
c
= 20
o
,
- gain margin M
c
= 4.45 dB,
- peak magnification ratio 3.39 at 1.48 rad/sec
Remark that all these performance indicators are
stated in the frequency domain and three of them deal
with open loop characteristics (ω
c
,Φ
c
,M
c
) while the
other are concerned with the closed loop properties.
Worth mentioning that there are only two free pa-
rameters of the model (1) while five conditions are
imposed. We may check them as follows. Since
ω
c
corresponds to 0 dB in the gain/log characteris-
tic, it follows that K/ω
c
= 1, hence K = ω
c
. On the
other hand, since the phase margin is 20
o
, the phase
should be −160
o
at the crossover frequency what will
give τω
c
= 70
o
hence τ = 7π/(18ω
c
). With this (1)
is completely determined and we have to check the
other properties. In order to verify the gain margin we
need the frequency of phase reversal (when the phase
equals −180
o
. It follows easily that τω
π
= π/2, there-
fore
ω
π
=
9
7
ω
c
, A(ω
π
) =
K
ω
π
=
ω
c
ω
π
=
7
9
(10)
hence M
c
= 20lg(9/7) = 2.18 dB. The condition on
the neutral stability frequency ω
0
has to indicate a tol-
erable increase of the gain provided the time lag is
kept constant or, conversely, a tolerable increase of
the time lag provided the gain is kept constant. The
closed loop characteristic equation is
s+ Ke
−τs
= 0 (11)
and the neutral stability will require a pair of zeros of
(11) on ıR hence the conditions
Kcos ω
0
τ = 0 , ω
0
− K sin ω
0
τ = 0 (12)
The first equality gives ω
0
τ which is substituted in the
second to obtain the admissible value of K since τ fol-
lows by fixing ω
0
. We may continue in this way by
checking the other conditions. Our aim however is to
check the usefulness of the proposed approach by ap-
plying Theorem 1. Considering the transfer function
of (1) we check the frequency domain inequality (9)
1+ Re
Ke
−ıωτ
ıω
= 1− Kτ
sin ωτ
ωτ
> 0 , ∀ω
and for it fulfilment it is necessary and sufficient to
have 1 − Kτ > 0 which is exactly (8). Taking into
account the computations of the linear case we find
that 1 − Kτ=1 − ω
c
τ=1 − 7π/18 < 0!. This is quite
unpleasant and it deserves some comment. Condi-
tion (8) accounts for the so-called limit stability prop-
erty (R˘asvan, 1975) - a necessary condition for abso-
lute stability within the sector (0,
¯
ϕ) - exponential sta-
bility for linear characteristics within arbitrarily small
sector (0,ε). A more general and less restrictive nec-
essary condition might be the so called minimal sta-
bility (Popov, 1973) which requires stability for a sin-
gle linear characteristic within the sector; neverthe-
less, if limit stability fails this will require a linear
characteristic within a sector (ϕ,
¯
ϕ) with ϕ > 0 and
this is unacceptable since the saturation nonlinearity
belongs to the sector (0,
¯
ϕ).
Coming back to the condition 1 − ω
c
τ > 0 which
does not hold, it follows that robustness assumed in
the linear case is not enough to ensure it in the PIO
II (system with rate limiter) case. If we require from
the beginning ω
c
τ < 1, the phase at the crossover fre-
quency will be larger than −(1+ π/2) rad hence the
phase margin has to be larger than π/2 − 1 rad i.e.
≈ 33
o
- a result that was at some extent expected.
A UNIFYING POINT OF VIEW IN THE PROBLEM OF PIO - Pilot In-the-loop Oscillations
203

4 CONCLUSIONS
This paper is demonstrating a point of view that
seemed very natural when absolute stability i.e. ro-
bust global asymptotic stability for systems with sec-
tor restricted nonlinear functions was investigated.
This point of view is that robust stability of linear
systems should imply the same property for non-
linear systems also, at least for those with sector
restricted nonlinearities. Such a point of view is
transparent throughout all research concerning the
so called Aizerman and Kalman problems (Popov,
1973),(R˘asvan, 1975) and geometric similarities of
the Nyquist and Popov frequency domain criteria
strengthened it. Stating it, obviously is not enough;
this position paper is pointing to critical analysis and
further research, mainly application oriented. We
have chosen the field of aircraft oscillations to illus-
trate this point of view for its practical importance
(proved by the intense research activities around PIO
problem) as well as for its feedback-based modeling
of the dynamics: control appears here as a genuine
hidden technology and hidden paradigm.
Since the field of aircraft dynamics and handling
qualities has very strict requirements and procedures,
the amount of the necessary research appears to be
high and with a certain degree of complexity. The
point of view stated here is to be applied possibly to
all cases of PIO I i.e. corresponding to fully linearized
systems; for the entire set of criteria, see (Anon.,
2000),(Klyde et al., 1995). But for each criterion one
may wish to consider several cases of pilot models.
For all these cases we have to consider the PIO II i.e.
the nonlinear, rate limited counterpart. But, besides
the comparison of the PIO I criteria and of their non-
linear counterpart, a comparison with the other PIO II
criteria, obtained independently of the approach pre-
sented in this paper is also necessary.
All this analysis and various comparison of the
criteria contain the necessary amount of critical
assessment of the present position paper proposal.
To this we add the specific PIO approach in aircraft
studies: conversion in a checkable form and applica-
tion on “real data” stored in the aviation databases.
Nevertheless it is hoped to follow the approach de-
scribed here in the next research on other PIO criteria.
REFERENCES
Anon. (2000). Flight Control Design - Best Practices.
NATO-RTO Technical Report 29, December 2000.
Klyde, D. H., McRuer, D. T., and Myers, T. T. (1995). Uni-
fied pio theory vol.i: Pio analysis with linear and non-
linear effective vehicle characteristics, including rate
limiting. Technical Report WL-TR-96-3028, AIAA.
Klyde, D. H., McRuer, D. T., and Myers, T. T. (1996). Pio
analysis with actuator rate limiting. Paper 96-3432-
CP, AIAA.
Klyde, D. H. and Mitchell, D. G. (2005). A pio case study
- lessons learned through analysis. Paper 05-661-CP,
AIAA.
McRuer, D. T. (1994). Pilot induced oscillations and human
dynamic behavior. Technical report CR-4683 Decem-
ber 1994, NASA.
McRuer, D. T., Klyde, D. H., and Myers, T. T. (1996). De-
velopment of a comprehensive pio theory. Paper 96-
3433-CP, AIAA.
Megretski, A. (1997). Integral quadratic constraints for
systems with rate limiters. Technical Report LIDS-
P-2407, Massachussets Institute of Technology, Cam-
bridge MA.
Megretski, A. and Rantzer, A. (1997). System analysis via
integral quadratic constraints. IEEE Transactions on
Automatic Control, 42(6):819–830.
Neal, T. P. and Smith, R. E. (1971). A flying qualities cri-
terion for the design of fighter flight control systems.
Journal of Aircraft, 8(10):803–809.
Popov, V. M. (1973). Hyperstability of Control Systems.
Springer Verlag, Berlin-Heidelberg-New York, 1st
edition.
R˘asvan, V. (1975). Absolute stability of time lag control sys-
tems (in Romanian). Editura Academiei, Bucharest,
1st edition.
Yakubovich, V. A. (1967). Frequency domain conditions for
absolute stability of control systems with several non-
linear and linear non-stationary blocks (in russian).
Avtomatika i Telemekhanika, 28(6):5–30.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
204