IMPLEMENTATION OF A HOMOGRAPHY-BASED VISUAL SERVO

CONTROL USING A QUATERNION FORMULATION

T. Koenig and G. N. De Souza

ViGIR Laboratory, University of Missouri, 349 Eng. Building West, Columbia-MO, U.S.A.

Keywords:

Image-base servo, visual servoing, quaternion.

Abstract: In this paper, we present the implementation of a homography-based visual servo controller as introduced in

(Hu et al., 2006). In contrast to other visual servo controllers, this formulation uses a quaternion representation

of the rotation. By doing so, potential singularities introduced by the rotational matrix representation can be

avoided, which is usually a very desirable property in, for example, aerospace applications such as for visual

control of satellites, helicopters, etc.

The movement of the camera and the image processing were performed using a simulation of the real envi-

ronment. This testing environment was developed in Matlab-Simulink and it allowed us to test the controller

regardeless of the mechanism in which the camera was moved and the underlying controller that was needed

for this movement. The ﬁnal controller was tested using yet another simulation program provided by Kawasaki

Japan for the UX150 industrial robot. The setup for testing and the results of the simulations are presented in

this paper.

1 INTRODUCTION

Any control system using visual-sensory feedback

loops falls into one of four categories. These cate-

gories, or approaches to visual servoing, are derived

from choices made regarding two criterias: the coor-

dinate space of the error function, and the hierarchical

structure of the control system. These choices will de-

termine whether the system is a position-based or an

image-based system, as well as if it is a dynamic look-

and-move or a direct visual servo (Hutchinson et al.,

1996).

For various reasons includingsimplicity of design,

most systems developed to date fall into the position-

based, dynamic look-and-move category (DeSouza

and Kak, 2004). In this paper however, we describe

an image-based, dynamic look-and-move visual ser-

voing system. Another difference between our ap-

proach and other more popular choices in the litera-

ture is in the use of a quaternion representation, which

eliminates the potential singularities introduced by a

rotational matrix representation (Hu et al., 2006).

We based the development of our controller on the

ideas introduced in (Hu et al., 2006), which requires

the assumption that a target object has four coplanar

and non-colinear feature points denoted by O

, where

i = 1. . . 4. The plane deﬁned by those 4 feature points

∗

◦

∗

◦

∗

◦

¯m

∗

¯m

Figure 1: Relationships between the frames and the plane.

is denoted by Π. Moreover, two coordinate frames

must be deﬁned: F (t) and

∗

F , where F (t) is af-

ﬁxed to the moving camera and

∗

F represents the

desired position of the camera. Figure 1 depicts the

aboveconcepts as well as the vectors

◦

¯m

(t),

∗

¯m

∈ R

representing the position of each of the four feature

points with respect to the corresponding coordinate

frames. That is:

◦

¯m

= [

◦

]

i = 1. . . 4 (1)

∗

¯m

= [

∗

]

i = 1. . . 4 (2)

The relationship between these two sets of vectors can

288

Koenig T. and N. De Souza G. (2008).

IMPLEMENTATION OF A HOMOGRAPHY-BASED VISUAL SERVO CONTROL USING A QUATERNION FORMULATION.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 288-294

DOI: 10.5220/0001503402880294

 SciTePress

be expressed as

◦

¯m

◦

∗

◦

∗

¯m

(3)

where

◦

∗

(t) is the translation between the two

frames, and

◦

∗

(t) is the rotation matrix which brings

∗

F onto F .

Intuitively, the control objective can be regarded

as the task of moving the robot so that

◦

¯m

(t) equals

∗

¯m

∀i as t → inf. However, an image-based vi-

sual servoing system is not expected to calculate the

real coordinates of these feature points. Instead, it

can only extract the image coordinates of those same

points. That is, the coordinates

◦

and

∗

of the

projection of the feature points onto the image plane,

given by:

◦

= A

◦

and

∗

= A

∗

, where A is the

matrix of the intrinsic parameters of the camera. So,

the real control objective becomes that of moving the

robot so that

◦

equals

∗

This idea will be further detailed in the following

section.

2 DESIGN OF THE

CONTROLLER

As mentioned above, the control objective is to reg-

ulate the camera to a desired position relative to the

target object. In order to achieve this control objective

the image coordinates at the desired position have to

be known. This can be done by taking an image of the

target object at the desired position and extracting the

feature points using an image processing algorithm.

Once a picture is taken and the image coordinates are

extracted, those coordinates can be stored for future

reference. It is assumed that the motion of the cam-

era is unconstrained and the linear and angular veloc-

ities of the camera can be controlled independently.

Furthermore the camera has to be calibrated, i.e. the

intrinsic parameters of the camera A must be known.

As we mentioned earlier, in the Euclidean space

the control objective can be expressed as:

◦

∗

(t) → I

as t → inf (4)

◦

∗

(t)|| → 0 as t → inf (5)

and the translation regulation error e(t) ∈ R

can be

deﬁned using the extended normalized coordinates as:

e =

◦

−

∗



◦

−

∗

◦

−

∗



◦

∗



(6)

The translation regulation objective can then be quan-

tiﬁed as the desire to regulate e(t) in the sense that

||e(t)|| → 0 as t → inf . (7)

It can be easily veriﬁed that if (7) is satisﬁed, the ex-

tended normalized coordinates will approach the de-

sired extended normalized coordinates, i.e.

◦

(t) →

∗

(t) and

◦

(t) →

∗

(t) (8)

as t → inf. Moreover, if (7) and (8) are satisﬁed,

(5) is also satisﬁed.

Similarly, the rotation regulation objective in (4)

can be expressed in terms of its quaternion vector q =

˜q ]

, ˜q = [q

]

(Chou and Kamel, 1991)

by:

|| ˜q(t)|| → 0 as t → inf . (9)

In that case, if (7) and (9) are satisﬁed, the control

objective stated in (4) is also satisﬁed.

For such translational and rotational control ob-

jectives, it was shown in (Hu et al., 2006) that the

closed-loop error system is given by:

˙q

˜q



− ˜q



−1

˜q (10)

˜q = −



− ˜q



− ˜q



−1

˜q (11)

∗

˙e = −K

e+ ˜z

(12)

and the control inputs by:

= −K



− ˜q



−1

˜q (13)

−1

∗

ˆz

) (14)

where

∗

ˆz

= e

is an estimation for the unknown

∗

; ˜q

is the anti-symmetric matrix representation

of the vector ˜q; L

, L

are the linear and angular

Jacobian-like matrices; K

, K

∈ R

3×3

are diagonal

matrices of positive constant control gains; and the

estimation error ˜z(t) ∈ R is deﬁned as ˜z

∗

−

∗

ˆz

A proof of stability for the controller above can be

found in (Hu et al., 2006).

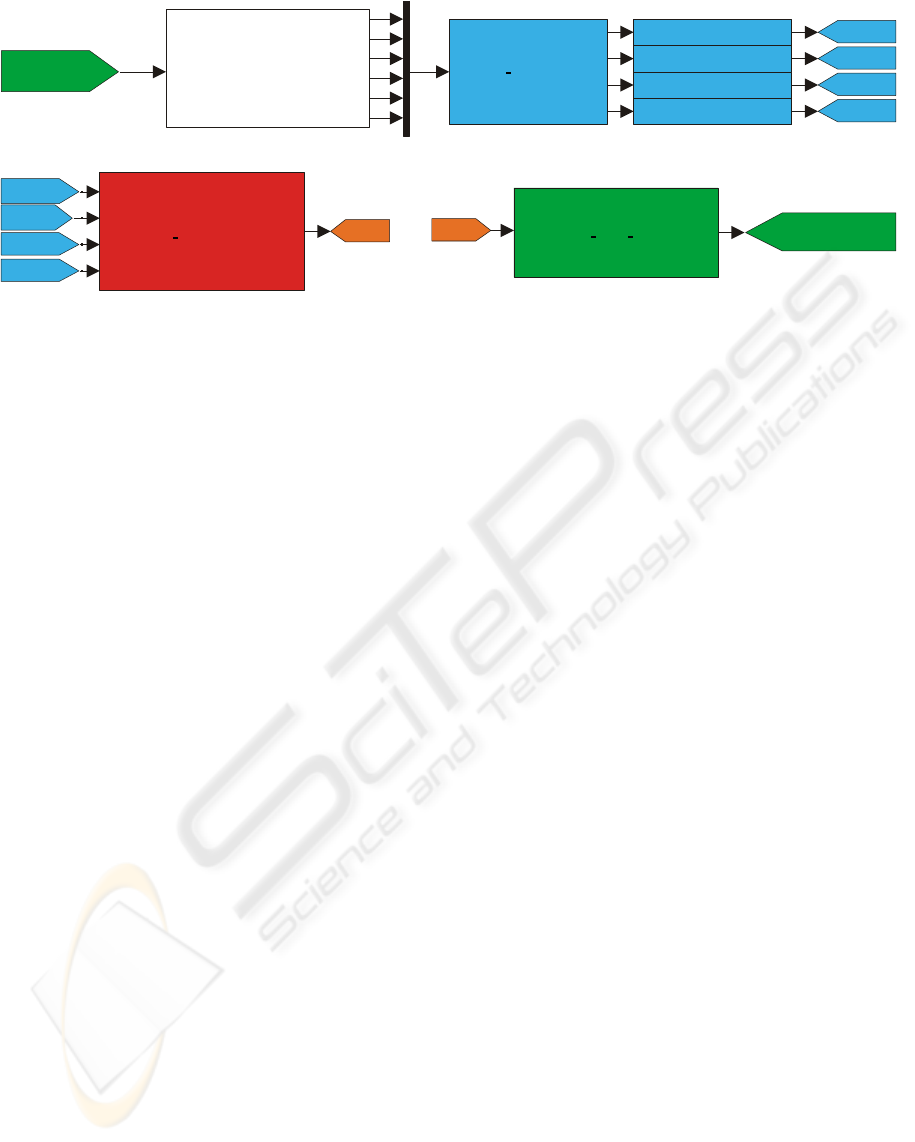
3 IMPLEMENTATION

In this work the task of controlling a robot with a

visual-servoing algorithm was divided into four ma-

jor parts:

1. Capturing images using a video camera.

2. Processing the images to get the coordinates of the

feature points.

3. Calculating the input variables, i.e. the velocities

of the robot endeffector.

4. Moving the robot according to the given input

variables.

IMPLEMENTATION OF A HOMOGRAPHY-BASED VISUAL SERVO CONTROL USING A QUATERNION

FORMULATION

289

discrete and noise

[CurrentFrame]

csfcn camera

CameraPose

simulate Frame

HTM to XYZOAT

[p1]

[p2]

[p3]

[p4]

[u]

csfcn

controller

msfcn

frame htm

Figure 2: The Simulink-Model.

The hardware available for this task consisted of a

Kawasaki industrial robot with a camera mounted on

its endeffector and vision-sensor network for captur-

ing and processing images from the camera.

The controller was implemented as a C++ class, in

order to guarantee the future reusablility of the code

in different scenarios (as it will be better explained be-

low). Initially, the controller requires the camera in-

trinsic parameters and the desired image coordinates

of the four feature points. Next it extracts the cur-

rent image coordinates and then it calculates the lin-

ear and angular velocities of the endeffector, i. e. the

input variables of the controller.

In order to safely test the controller, the real pair

robot/camera was replaced by two different simula-

tors. The ﬁrst simulator, which was implemented in

MATLABSIMULINK, simulates an arbitrary motion of

the camera in space. The camera is represented by a

coordinate frame as it is brieﬂy described later. With

this simulator it is possible to move the camera ac-

cording to the exact given velocities.

In all testing scenarios performed, the camera sim-

ulator needed to output realistic image coordinates of

the feature points. To achieve that, the simulator re-

lied on a very accurate calibration procedure (Hirsh

et al., 2001) as well as exact coordinates of the feature

points in space with respect to the camera. Given that,

the simulator could then return the image coordinates

of the feature points at each time instantt. The camera

simulator was also implemented as a C++ class.

The second simulator is a program provided by

Kawasaki Japan. This simulator can execute the ex-

act same software as the real robot and therefore it

allowed for the testing of the code used to move the

real robot. This code is responsible for performing

the forward and inverse kinematics, as well as the dy-

namics of the robot.

The basic structure of the simulink model can be

seen in Figure 2.

In this work, we will not report the resultis from

the tests with the real robot. So, in order to demon-

strate the system in a more realistic setting, noise was

added to the image processing algorithm and a time

discretization of the image acquisition was introduced

to simulate the camera.

3.1 Describing the Pose and Velocity of

Objects

The position and orientation (pose) of a rigid ob-

ject in space can be described by the pose of an at-

tached coordinate frame. There are several possible

notations to represent the pose of a target coordinate

frame with respect to a reference one, including the

homogeneous transformation matrix, Euler Angles,

etc. (Saeed, 2001) and (Spong and Vidyasagar, 1989).

Since we were using the Kawasaki robot and simula-

tor, we adopted the XYZOAT notation as deﬁned by

Kawasaki. In that system, the pose of a frame F with

respect to a reference frame

∗

F is described by three

translational and three rotational parameters. That is,

the cartesian coordinates X, Y, and Z, plus the Orien-

tation, Approach, and Tool angles in the vector form:

X =



x y z φ θ ψ



This notation is equivalent to the homogeneous

transformation matrix:

H =







CφCθCψ−SθSψ −CφCθSψ− SφCψ CφSθ x

SφCθCψ+ CθSψ −SφCθSψ+ CφCψ SφSθ y

−SθCψ SθSψ Cθ z

0 0 0 1







(15)

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

290

where Sα = sin(α) and Cα = cos(α) and the an-

gles φ, θ, and ψ correspond, respectively, to O, A, and

T and represent:

• Rotation of φ about the ¯a-axis (z-axis of the mov-

ing frame) followed by

• Rotation of θ about the ¯o-axis (y-axis of the mov-

ing frame) followed by

• Rotation of ψ about the ¯a-axis (z-axis of the mov-

ing frame).

4 RESULTS

The controller was tested in three different scenarios:

pure linear movement; pure angular movement; and

combined movement. In all these cases, the camera

intrinsic parameters were:

A =





122.5 −3.7737 100

0 122.6763 100

0 0 1





(16)

The four feature points were arranged in a square

around the origin of the reference frame and had co-

ordinates:

= [−5 − 5 0]

= [5 5 0]

= [5 − 5 0]

= [−5 5 0]

(17)

The desired pose of the camera was the same for

all the simulations, only the start poses differ. The

desired pose of the camera was 20 units above the tar-

get object, exactly in the middle of the four feature

points. The camera was facing straight towards the

target object, i.e. its z-axis was perpendicular to the

xy-plane and pointing out. The x-axis of the camera

was antiparallel to the x-axis of the reference frame

and the y-axis parallel to the y-axis of the reference

frame. This pose can be described by:

∗



0 0 20 0

◦

180

◦



(18)

The control gains used for the controller were:





25 0 0

0 25 0

0 0 25





(19)





1.5 0 0

0 1.5 0

0 0 1.5





(20)

As mentioned in Section 3, we simulated both the

noisy and the discrete aspects of a real camera. That

is, we added noise to the image coordinates to simu-

late a typical accuracy of 0.5 pixels within a random

error of 2 pixels in any direction. These values were

obtained experimentally using real images and a pre-

viously developed feature extraction algorithm.

start position

desired position

−15

−5

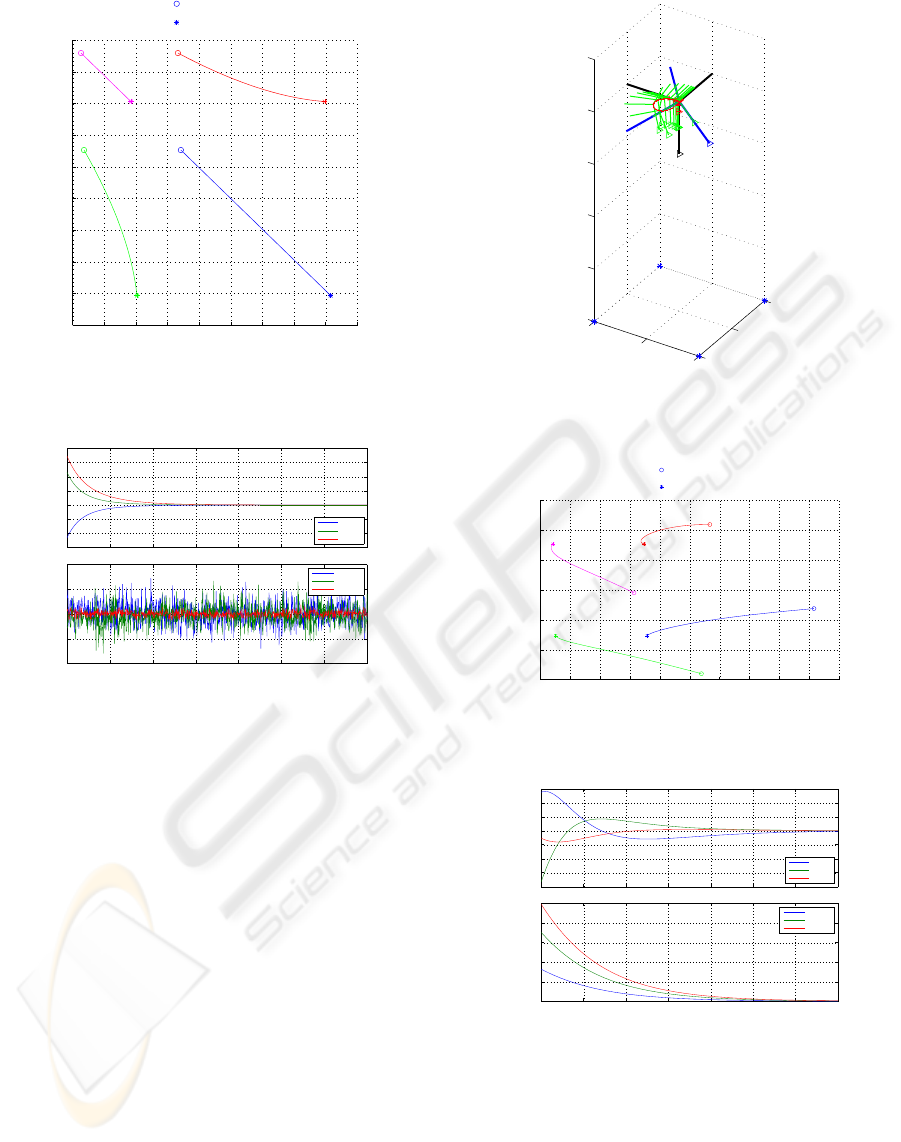
Figure 3: Linear motion simulation in euclidean space.

4.1 Linear Motion

In this simulation the camera did not rotate, i.e. the

orientation of the camera in the start pose was the

same as in the desired pose. The camera was sim-

ply moved 20 units along the z-axis of the reference

frame and -10 units along the x- and the y-axis of the

reference frame. The start pose was given by

◦



−10 −10 40 0

◦

180

◦



(21)

Figure 3 shows the pose of the camera at ten time

instants. The z-axis of the camera – the direction in

which the camera is “looking” – is marked with a

triangle in the ﬁgure. The four points on the target

object, lying in the xy-plane, are marked with a star.

In Figure 4 the image coordinates of the four points

are shown. The image coordinate at the start pose is

marked with a circle, the image coordinate at the de-

sired pose with a star.

In Figure 5 the control inputs are shown. The ﬁrst

part shows the linear velocities, the second part the

angular velocities of the camera.

IMPLEMENTATION OF A HOMOGRAPHY-BASED VISUAL SERVO CONTROL USING A QUATERNION

FORMULATION

291

u [pixel]

v [pixel]

start coordinates

desired coordinates

100

120

140

Figure 4: Coordinates of the feature points in image space

for the linear motion.

t [s]

−20

−4

×10

−15

Figure 5: Control input for the linear motion.

4.2 Angular Motion

In this simulation the start position of the camera was

identical to the desired position, only the orientation

differed. The start pose is given by:

◦



0 0 20 45

◦

150

◦



(22)

As in Section 4.1 the ﬁgures 6, 7 and 8 show the

movement of the camera in euclidean space, the im-

age coordinates of the four feature points and the con-

trol variables.

4.3 Coupled Motion

In this simulation the camera could perform any

generic movement, i.e. both the position and the ori-

entation at the beginning differ from the desired pose

of the camera. The start pose is given by:

◦



10 −10 40 90

◦

140

◦



(23)

start position

desired position

−5

Figure 6: Angular motion simulation in euclidean space.

u [pixel]

v [pixel]

start coordinates

desired coordinates

100

120

140

160

200 240

Figure 7: Coordinates of the target points in image space

for the angular motion.

t [s]

−4

−2

0.2

0.4

Figure 8: Control input for the angular motion.

As in Section 4.1 the ﬁgures 9, 10 and 11 show

the movement of the camera in euclidean space, the

image coordinates of the four feature points and the

control variables.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

292

start position

desired position

−10

Figure 9: Coupled motion simulation in euclidean space.

u [pixel]

v [pixel]

start coordinates

desired coordinates

100

120

140

160 200

Figure 10: Coordinates of the target points in image space

for the coupled motion.

t [s]

0.4

0.8

5 6

Figure 11: Control input for the coupled motion.

4.4 Inﬂuence of Noise

The setup for this simulation is the same as in Sec-

tion 4.3, but with noise added to the pixels. That is,

at each discrete time an image is grabbed a random

Gaussian noise N(0.5,2) is added to the pixel coordi-

nates.

As in Section 4.1 the ﬁgures 12, 13 and 14 show

the movement of the camera in euclidean space, the

image coordinates of the four feature points and the

control variables.

start position

desired position

−15

−10

−5

Figure 12: Coupled motion with noise simulation in eu-

clidean space.

u [pixel]

v [pixel]

start coordinates

desired coordinates

100

120

140

140 160 180 200

Figure 13: Coordinates of the target point in image space

for the coupled motion with noise.

t [s]

0.4

0.8

1.2

Figure 14: Control input for the coupled motion with noise.

IMPLEMENTATION OF A HOMOGRAPHY-BASED VISUAL SERVO CONTROL USING A QUATERNION

FORMULATION

293

5 CONCLUSIONS

An implementation of an image-based visual servo

controller using Matlab and C++ was presented. Var-

ious simulations with and without noise were con-

ducted and the controller achieved asymptotic regula-

tion in all cases. This implementation experimentally

validates the controller developed in (Hu et al., 2006)

and now that the controller is safe to use, new experi-

menations using the real robot can be carried out.

At this point, the control gains were kept small and

the discretized intervals were based on a normal cam-

era (30fps). Those choices let us achieve a conver-

gence in less than 7 seconds. However, for real-world

applications, those same choices must be revised so

that the convergence can be made a lot faster.

The control model and all software modules used

in this paper will be made available on line at

http://vigir.missouri.edu

REFERENCES

Chou, J. C. K. and Kamel, M. (1991). Finding the posi-

tion and orientation of a sensor on a robot manipulator

using quaternions. International Journal of Robotics

Research, 10(3):240–254.

DeSouza, G. N. and Kak, A. C. (2004). A subsumptive,

hierarchical, and distributed vision-based architecture

for smart robotics. IEEE Transactions on Systems,

Man and Cybernetics - Part B, 34(5).

Hirsh, R., DeSouza, G. N., and Kak, A. C. (2001). An it-

erative approach to the hand-eye and base-world cal-

ibration problem. In Proceedings of 2001 IEEE In-

ternational Conference on Robotics and Automation,

volume 1, pages 2171–2176. Seoul, Korea.

Hu, G., Dixon, W., Gupta, S., and Fitz-Coy, N. (2006). A

quaternion formulation for homography-based visual

servo control. In IEEE International Conference on

Robotics and Automation, pages 2391–2396.

Hutchinson, S., Hager, G. D., and Corke, P. (1996). A tu-

torial on visual servo control. IEEE Transactions on

Robotics & Automation, 12(5):651–670.

Saeed, B. (2001). Introduction to Robotics, Analysis, Sys-

tems, Applications. Prentice Hall Inc.

Spong, M. W. and Vidyasagar, M. (1989). Robot Dynamics

and Control. John Wiley & Sons.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

294