USING THE OAG TO BUILD A MODEL DEDICATED TO MODE
HANDLING OF FMS
Nadia Hamani
Departement of Informatics, Paris X University, 200 avenue de la République, 92001 Nanterre, France
Nathalie Dangoumau, Etienne Craye
LAGIS, Ecole Centrale de Lille, BP48 cité scientifique, Villeneuve d’Ascq, France
Keywords: Flexible Manufacturing Systems, control system, supervision, mode handling, functional modeling.
Abstract: This paper deals with a modeling approach for mode handling of Flexible Manufacturing Systems (FMS).
We show that using the plant model enables to establish aggregate operations. These are generic entities
which depend only on the plant and do not depend on production goals. Aggregate operations are then used
to build the model dedicated to mode handling. This study is illustrated through an example of a flexible
manufacturing cell.
1 INTRODUCTION
We are interested in problems of monitoring and
supervision in a fault tolerant control system
dedicated to Flexible Manufacturing Systems
(FMS) (Ranky, 1990). According to our approach,
the supervision is made up of three functions:
decision, piloting, and mode handling. The
monitoring function (Elkhattabi et al., 1995;
Toguyeni et al., 1996) detects and localizes the
failures at the plant level. The decision function
(Berruet et al., 2000) determines the new
configuration of the FMS. The functions of mode
handling and piloting (Tawegoum et al., 1994)
implement the decisions about the new
configuration of the FMS.
In order to achieve the role of mode handling
within the control system, one should provide
models representing the operating modes of the
production system and its subsystems. The existing
modeling approaches of operating modes of
Automated Production Systems (APS) are
compared in (Hamani et al., 2006). The advantages
of functional modeling approaches are showed.
Such approaches are concerned with the services
delivered by the FMS rather than production means.
Our approach (Hamani et al., 2006) is based on a
functional modeling method. This approach is well
adapted to FMSs because it is based on the mission
concept (a production goal) which represents the
flexibility which characterizes the FMS production.
The obtained model is generic. For a given FMS,
the predefined functional subsystems (called
entities) are instantiated to generate the model. An
aggregate operation is a generic entity depending
only on the plant and not on production goals.
The purpose of this paper is to present a method
to calculate aggregate operations from the plant
model. The paper is organized as follows. Section 2
reminds the basic concepts of our modeling method
and the steps of building the FMS functional model.
Section 3 presents a method to determine aggregate
operations from the plant model. An example of a
flexible manufacturing cell is used to illustrate this
study.
2 THE FMS MODEL
2.1 Basic Concepts
An FMS produces simultaneously a set of parts.
Usually we desire to change production goals. That
is why the mission concept is introduced in
(Hamani et al., 2006). A mission (M) is the subset
of Logical Operating Sequences (LOS) which are
282
Hamani N., Dangoumau N. and Craye E. (2008).
USING THE OAG TO BUILD A MODEL DEDICATED TO MODE HANDLING OF FMS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 282-287
DOI: 10.5220/0001503302820287
Copyright
c
 SciTePress

produced simultaneously. A LOS is a set of ordered
machining functions performed on some parts. A
LOS is noted LOS f
1
...f
n
or LOS f
i
(i = 1, n).
With each function of a Logical Operating
Sequence is associated its possible achievements.
They are aggregate operations for which the
machining operation is defined. An aggregate
operation is a generic entity which depends only on
the FMS plant and not on production goals. An
aggregate operation corresponding to a machining
Major Characteristic Area (MCA) noted
Op
MCA_machining
is a set of the corresponding
elementary machining operations and Access
Transfers. MCA concept is defined in (Hamani et
al., 2006).
In an FMS, an operation (Op) is defined as a
function carried out by a resource (Berruet et al.,
2000; Toguyeni et al., 2003). An operation is noted
Op
Ri, fi
where f
i
is the performed function and R
i
the
resource which implements it. An elementary
operation is an operation carried out only once,
continuously, i.e. without the possibility to choose
another alternative during the normal execution of
the operation.
Access Transfers (TrA) associated with a
machining area (or a MCA), noted TrA
machining_MCA
,
correspond to the set of elementary transfer
operations that connect this area to the other MCA
of the FMS. An elementary transfer (TrE) is
performed by one resource between two MCA. An
elementary transfer is noted
DS
i
R
TrE
→
with S a source
CA, D a destination CA, and R
i
the transfer
resource.
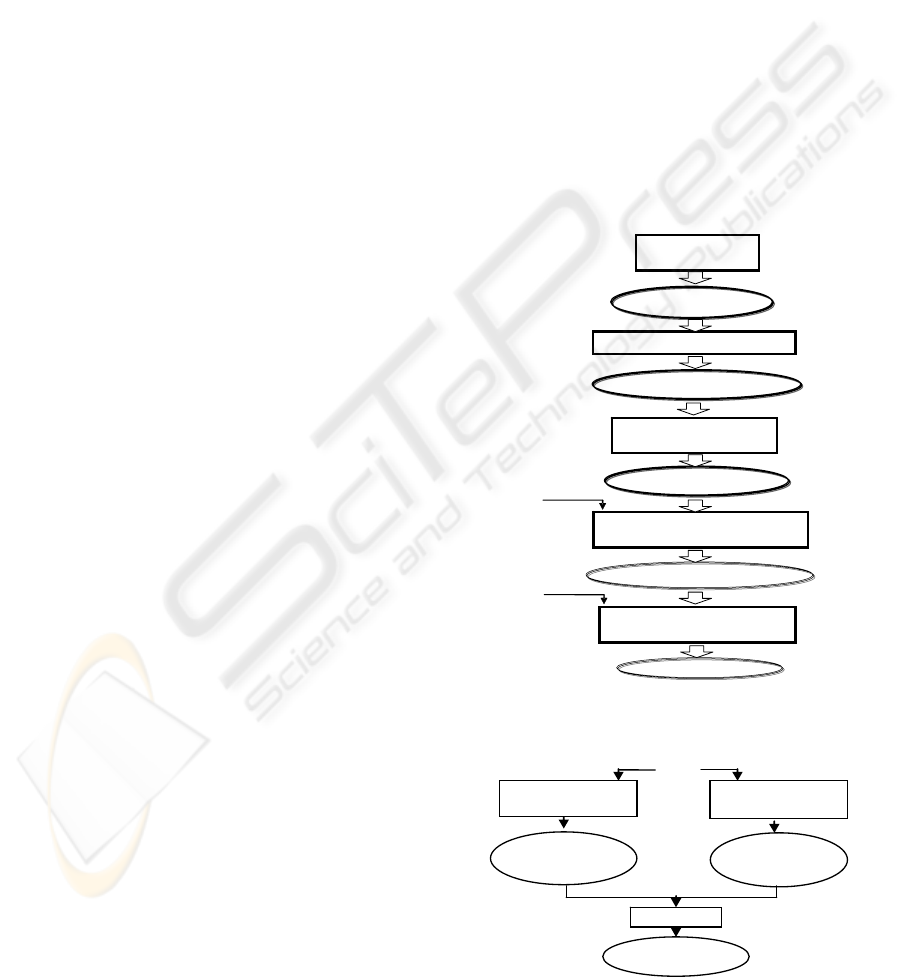
2.2 The Specification Steps
The specification steps (Figure 1) of the FMS
functional model are described in the following.
1
st
Step: Identification of the entities of the model
- list the missions that the FMS should carry out
- list for each mission its corresponding Logical
Operation Sequences
- for each Logical Operating Sequence identify the
corresponding machining functions
A machining function is implemented by one or
several elementary machining operations. Each one
is belonging to an aggregate operation.
- identify the aggregate operations of the FMS (see
the 2
nd
step)
- for each aggregate operation, identify the
resources which perform it (see the 3
rd
step)
2
nd
Step: Determination of aggregate operations
(Figure 2). For each machining area of the FMS:
- identify elementary machining operations which
are performed in this area
- identify the Access Transfers related to this area
- gather elementary machining operations together
with Access Transfers identified previously to
obtain aggregate operations
3
rd
Step: Determination of the resources that
perform elementary operations
For each aggregate operation:
- associate with each elementary machining
operation the resource or the configuration of the
resource (in the case of a polyvalent resource)
which performs it
- associate also with each elementary transfer
operation the resource (or the resources) which
performs it, redundant resources are linked with a
logical OR.
The aggregate
operations
of the FMS
The FMS
resources
Set of missions
Determination o
f
FMS mission
s
Determination of logical sequences
Set of lo
g
ical sequences
Determination of a
gg
re
g
ate
operations
Set of a
gg
re
g
ate operations
Determination of machinin
g
and
transfer resources
Set of resources
Determination of machinin
g
functions
Set of functions
Figure 1: Specification steps of the FMS entities.
Set of machining
operations
Determination of
machining operations
Set of access
transfers
Machin ing area
Determination of access
transfers
Aggregate operation
Gathering
Figure 2: Aggregate operations specification.
USING THE OAG TO BUILD A MODEL DEDICATED TO MODE HANDLING OF FMS
283

The functional model of the machining cell is
represented using the following entities:
• The missions
• The Logical Operating Sequences
• The machining functions
• The aggregate operations
- elementary machining operations
- Access Transfers (set of transfer operations)
• Transfer resources, machining resources
2.3 Illustration Example
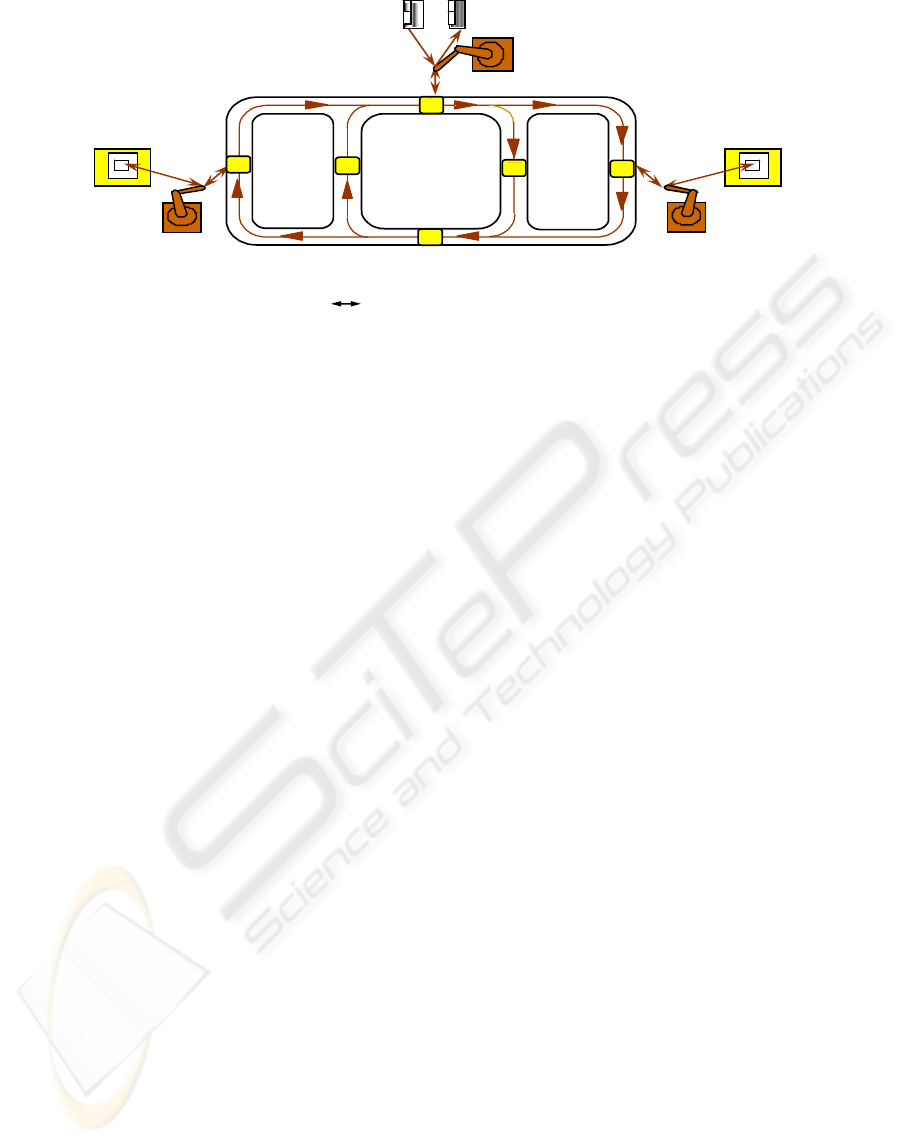
Consider an example of a flexible manufacturing
cell (Figure 3) with two machines M
1
and M
2
and
INPUT/OUTPUT buffers. The machines are loaded
with a transport system using three robots R
1
, R
2
and R
3
and a conveyer (CV). Moving directions of
CV are Z
1
→ (Z
2
or Z
5
), (Z
2
or Z
5
)Æ Z
3
, Z
3
→ (Z
4
or
Z
6
), (Z
4
or Z
6
)Æ Z
1
. It is assumed that M
1
is loaded
with R
1
and M
2
is loaded with R
2
. The parts are
loaded on the conveyor using the robot R
3
. The
machining functions performed by the system are
turning (t) and milling (m). Turning is carried out
by M
1
, milling by M
1
and M
2
.
According to the functional requirements of this
illustration example, three missions can be required
by the operator: M
1
, M
2
and M
3
. The corresponding
Logical Operating Sequences are the following:
M
1
: LOS
1
and LOS
2
, M
2
: LOS
1
, LOS
2
and LOS
12
and M
3
: LOS
1
, LOS
12
and LOS
21
The machining functions which compose each
Logical Operating Sequence are the following:
LOS
1
: turning; LOS
2
: milling; LOS
12
: turning then
milling; LOS
21
: milling then turning.
Turning function is performed by the
elementary machining operation Op
M1,t
belonging to
the aggregate operation Op
M1
. Milling function is
performed by the elementary machining operation
Op
M1,m
belonging to the aggregate operation Op
M1
or by the elementary machining operation Op
M2,m
belonging to the aggregate operation Op
M2
.
For the machining area M
1
: the elementary
machining operations performed by M
1
are Op
M1,t
and Op
M1,m
. Access Transfers related to M
1
are
1
M
TrA = AND (
1
Msource_MCA
Tr
→
,
ndestinatio_MCA
1
M
Tr
→
).
This notation is using the logical AND and OR
and also three distinct levels: ‘{’ for the first level,
‘[’ for the second level and ‘(’ for the third level.
Section 3 presents a method to determine TrA
using the plant model.
The aggregate operation related to the
machining area M
1
is Op
M1
= AND [OR (Op
M1,t
,
Op
M1,m
) ,
1
M
TrA ]. The aggregate operation related to
the machining area M
2
is obtained in the same
manner.
Op
M1
is performed by the following resources:
the polyvalent machining resource M
1
performs the
elementary operations Op
M1,t
et Op
M1,m
. For transfer
resources: R
1
performs the elementary transfer
operations
1
M
2
Z
1
R
TrE
→
and
2
Z
1
M
1
R
TrE
→
; R
2
performs the
elementary transfer operations
4
Z
2
M
2
R
TrE
→
and
2
M
4
Z
2
R
TrE
→
; R
3
performs the elementary transfer
operations
1
ZIN
3
R
TrE
→
and
OUT
1
Z
3
R
TrE
→
; CV performs
the elementary transfer operations
2
Z
1
Z
CV
TrE
→
,
3
Z
2
Z
CV
TrE
→
,
5
Z
1
Z
CV
TrE
→
,
3
Z
5
Z
CV
TrE
→
,
4
Z
3
Z
CV
TrE
→
1
Z
4
Z
CV
TrE
→
,
6
Z
3
Z
CV
TrE
→
and
1
Z
6
Z
CV
TrE
→
.
The obtained model (AND/OR graph) for the
machining cell is represented in Figure 4. The
underlined entities are not developed. AND nodes
do not have any notation, however OR nodes are
denoted using +. These nodes correspond to an
M
1
FIFO INPUT
FIFO_OUTPUT
M
2
R
1
R
2
R
3
Z2 Conve
y
er
CV
Z1
Z5
Z4 Z6
Z3
R
robot
M machining resource
Z zone
Accessibilit
y
relation
Figure 3: An example of a flexible cell.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
284

inclusive OR or an exclusive OR according to the
constraints given in the functional requirements.
For example, an exclusive logical OR is necessary
for safety reasons, like two machining operations
which are performed by the same resource for
instance.
LOS
1
LOS
2
LOS
12
The cell
turning
milling
Op
M1
Op
M2
+
+
LOS
21
TrA
M2
M
1
M
2
M
3
+
Op
M2,m
TrA
M1
Op
M1,m
Op
M1,t
+
Figure 4: An extract of the functional model of the
machining cell.
3 DETERMINATION OF ACCESS
TRANSFERS
In order to determine TrA, a first step consists in
listing symmetrical transfers between MCA
representing both source and destination areas.
Then it is necessary to refine these transfers until
obtaining elementary transfer operations.
Once Access Transfers are determined, it is
necessary to identify elementary transfers which
compose them. If there is a direct accessibility
between two MCA then Tr
MCA_source→MCA_destination
corresponds to an elementary transfer. If not, it is
necessary to refine the transfers between the
Characteristic Areas until obtaining elementary
transfers. The possible paths are then established
and those which are redundant are linked together
with a logical OR. For example:
1
MIN
Tr
→
= AND (
1
ZIN
3
R
TrE
→
,
2
Z
1
Z
CV
TrE
→
,
1
M
2
Z
1
R
TrE
→
).
Due to increasing complexity of FMS, it could
be difficult to identify all the elementary transfers
which compose Access Transfers. That is why we
propose to determine them from the Operational
Accessibility Graph (OAG) (Berruet et al., 2000), a
graph which represents the FMS plant. The OAG
formalizes all the accessibilities between the
characteristic areas more precisely than informal
specifications provided in the functional
requirements.
To build an OAG, a partition of all elementary
operations is carried out and the concept of node is
introduced to simplify the modeling process. This
concept is defined in the following.
A node consists of an elementary operation or
some elementary operations. This regrouping is
governed by rules about the operations taxonomy
(Berruet et al., 2000; Toguyéni et al., 2003). The
nodes form OAG entities and allow relating the
operations using accessibility relations.
Based on this definition, several nodes are
defined: storage, machining, assembly, link, and
transfer nodes. The nodes are then linked together
using accessibility relations in order to build the
OAG.
3.1 The Operational Accessibility
Graph
The Operational Accessibility Graph (OAG) is a
directed graph where nodes are subsets of
operations performed by the resources of the
system and the arcs represent the accessibility
relations between operations (Toguyéni et al.,
2003). The OAG represents all the flexibilities of an
existing plant or a plant being designed. It is
obtained following these steps:
1
st
step- Identification of elementary operations
of the FMS: in this step elementary operations of
machining, storage (passive, active), and transfer
are identified.
2
nd
step- Regrouping the elementary operations:
the elementary operations carried out on the same
area and the equivalent elementary transfer
operations are gathered. A partition of all the
operations is thus obtained.
3
rd
step- Building the graph: a node is
associated with each operations subset established
in the previous step. The nodes of the OAG are thus
obtained. Then these nodes are connected with
respect to the accessibility between operations. The
OAG structure is then determined.
The method is applied to the illustration
example (Figure 3).
1) The elementary machining operations are
already identified (Op
M1,t
, Op
M1,m
, Op
M2,m
) and the
elementary transfer operations (
2
Z
1
M
1
R
TrE
→
,
1
M
2
Z
1
R
TrE
→
,
4
Z
2
M
2
R
TrE
→
,
2
M
4
Z
2
R
TrE
→
,
1
ZIN
3
R
TrE
→
,
OUT
1
Z
3
R
TrE
→
,
2
Z
1
Z
CV
TrE
→
,
3
Z
2
Z
CV
TrE
→
,
5
Z
1
Z
CV
TrE
→
3
Z
5
Z
CV
TrE
→
,
4
Z
3
Z
CV
TrE
→
,
1
Z
4
Z
CV
TrE
→
,
6
Z
3
Z
CV
TrE
→
,
1
Z
6
Z
CV
TrE
→
).
USING THE OAG TO BUILD A MODEL DEDICATED TO MODE HANDLING OF FMS
285

It is necessary to add the following storage
operations:
- Storage IN and storage OUT which are passive;
- Storage Z
1
, storage Z
2
, storage Z
3
, storage Z
4
,
storage Z
5
and storage Z
6
which are active.
2) Concerning the regroupings:
- One gathers Op
M1,t
and Op
M1,m
in a complex
operation on M
1
.
- Linking operations are: Link Z
1
, Link Z
2
, Link Z
3
,
Link Z
4
, Link Z
5
and Link Z
6
.
- The functions fulfilled by the elementary transfer
operations are all distinct. There is no regrouping
of transfers.
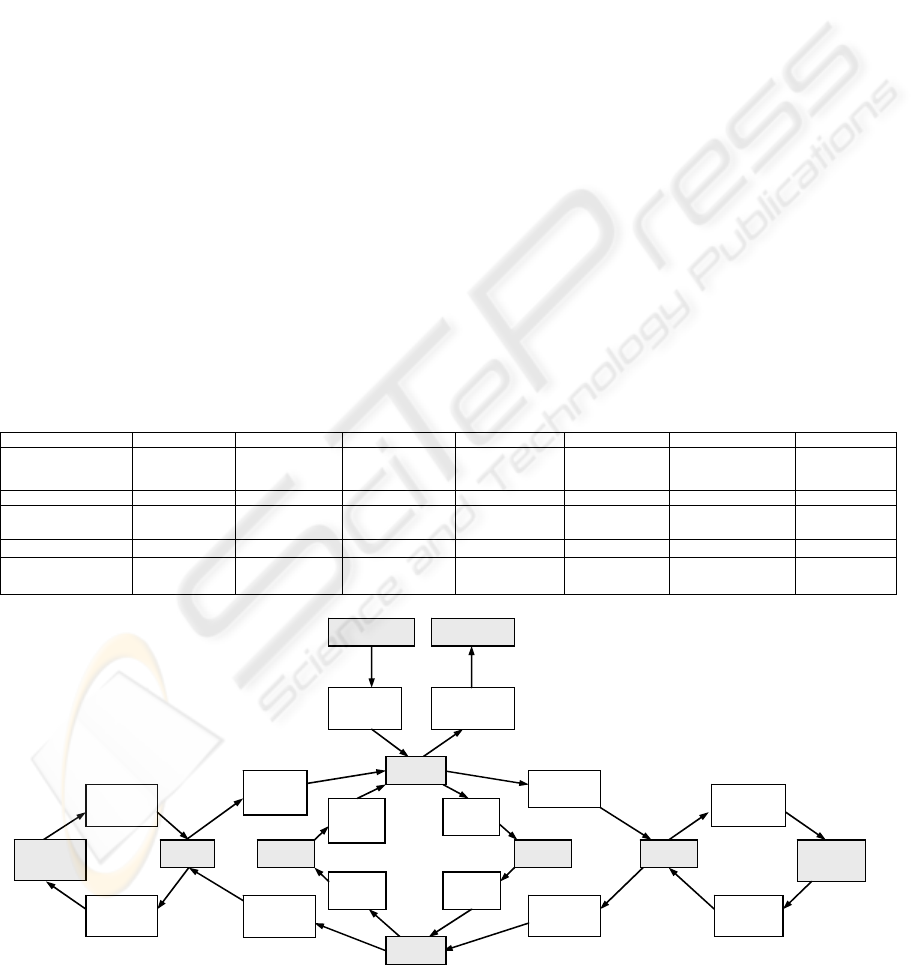
3) Table 1 summarizes the correspondence
between the nodes and the operations which
compose them. The resulting OAG is represented in
Figure 5.
Note: on Figure 5, storage nodes IN and OUT, link
nodes as well as machining nodes correspond to
characteristic areas of the cell. The subset formed
only by storage nodes and machining nodes
corresponds to main characteristic areas.
The obtained model is used to calculate the
elementary transfers as shown in the following.
3.2 A Procedure for Determination
Elementary Transfers
Based on the OAG, the following procedure is
proposed in order to calculate Access Transfers.
Beginning of the procedure:
1st Step: determination of Access Transfers associated
with machining nodes
For each machining node of the OAG:
- determine the paths which connect it with the others
machining nodes and the input of the cell;
- determine the paths which enable unloading parts
onto other machining nodes and the output of the cell;
The obtained paths are linked with a logical OR;
End For;
2
nd
Step: determination of elementary transfers which
compose the Access Transfers:
Do again for each identified path in the previous step
If the path relates two successive nodes of the OAG
Then the path is an elementary transfer
If not determine the paths which compose it
The redundant transfers are linked with a logical
OR; do not consider the paths which go over a
transfer node twice and those that contain
intermediary machining nodes;
Until all the obtained paths are elementary.
End of the procedure.
Table 1: The correspondence between nodes and operations.
N1 N2 N3 N4 N5 N6 N7 N8
Storage IN
1
ZIN
3
R
TrE
→
Link Z
1
2
Z
1
Z
CV
TrE
→
Link Z
2
1
M
2
Z
1
R
TrE
→
Machining M
1
Op
M1,t
Op
M1,m
2
Z
1
M
1
R
TrE
→
N9 N10 N11 N12 N13 N14 N15 N16
5
Z
1
Z
CV
TrE
→
Link Z
5
3
Z
2
Z
CV
TrE
→
3
Z
5
Z
CV
TrE
→
Link Z
3
4
Z
3
Z
CV
TrE
→
Link Z
4
2
M
4
Z
2
R
TrE
→
N17 N18 N19 N20 N21 N22 N23 N24
Machining M
2
Op
M2,m
4
Z
2
M
2
R
TrE
→
6
Z
3
Z
CV
TrE
→
Link Z
6
1
Z
6
Z
CV
TrE
→
1
Z
4
Z
CV
TrE
→
OUT
1
Z
3
R
TrE
→
Storage OUT
17
OUT
1
Z
3
R
TrE
→
1
ZIN
3
R
TrE
→
Turning
Milling
on M
1
2
Z
1
M
1
R
TrE
→
1
M
2
Z
1
R
TrE
→
12
8
3
6
Link Z
2
Storage OUT Storage IN
23
24
20
2
21
5
19
10
Link Z
4
4
Z
2
M
2
R
TrE
→
2
M
4
Z
2
R
TrE
→
18
15
16
13
7
Millin
g
on M
2
14
1
Z
6
Z
CV
TrE
→
6
Z
3
Z
CV
TrE
→
11
5
Z
1
Z
CV
TrE
→
3
Z
5
Z
CV
TrE
→
9
Link Z
6
2
Z
1
Z
CV
TrE
→
3
Z
2
Z
CV
TrE
→
Link Z
5
4
Z
3
Z
CV
TrE
→
1
22
4
1
Z
4
Z
CV
TrE
→
Link Z
3
Link Z
1
Figure 5: The OAG of the illustration example.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
286

For each machining node, the access paths
which are associated with it, added with machining
operations carried out on this node, are linked with
logical AND. This regrouping is an aggregate
operation.
For the illustration example, the access paths
calculated in the first step of the procedure for the
machining area M
1
are the following: OR
(
1
MIN
Tr
→
,
12
MM
Tr
→
) and OR (
2
M
1
M
Tr
→
,
OUT
1
M
Tr
→
). The
following elementary transfers are then obtained
using the second step of the procedure.
1
MIN
Tr
→
= AND (
1
ZIN
3
R
TrE
→
,
2
Z
1
Z
CV
TrE
→
,
1
M
2
Z
1
R
TrE
→
);
12
MM
Tr
→
= AND (
4
Z
2
M
2
R
TrE
→
,
1
Z
4
Z
CV
TrE
→
,
2
Z
1
Z
CV
TrE
→
,
1
M
2
Z
1
R
TrE
→
);
21
MM
Tr
→
= AND (
2
Z
1
M
1
R
TrE
→
,
3
Z
2
Z
CV
TrE
→
,
4
Z
3
Z
CV
TrE
→
,
2
M
4
Z
2
R
TrE
→
);
OUTM
1
Tr
→
= AND {
2
Z
1
M
1
R
TrE
→
,
3
Z
2
Z
CV
TrE
→
, OR [AND (
4
Z
3
Z
CV
TrE
→
,
1
Z
4
Z
CV
TrE
→
), AND
(
6
Z
3
Z
CV
TrE
→
,
1
Z
6
Z
CV
TrE
→
)],
OUT
1
Z
3
R
TrE
→
}.
Finally,
1
M
TrA = AND [OR (
1
MIN
Tr
→
,
12
MM
Tr
→
), OR
(
2
M
1
M
Tr
→
,
OUT
1
M
Tr
→
)].
4 CONCLUSIONS
In this paper our modeling method dedicated to
FMS
mode handling is extended. The FMS
functional model is obtained by a modular and
hierarchical decomposition leading to the
elementary machining and transfer operations. For
large scale systems, it is difficult to obtain all
possible redundancies of a plant. So we propose to
determine aggregate operations associated with
machining areas from the plant model represented
by the OAG. The aggregate operations are generic
concepts which depend only on the plant and not on
production goals. Such method enables to generate
automatically aggregate operations for an existing
system or a system being designed. The proposed
modeling steps are then illustrated through an
example of a manufacturing cell.
Further works aim at implementing the proposed
method within the information system
CASPAIM_soft (Ndiaye et al., 2002).
REFERENCES
Berruet, P., Toguyéni, A.K.A., Craye, E., 2000. Towards
implementation of recovery procedures for FMS
supervision. Computers in Industry, 43, 227-236.
Elkhattabi, S., Craye, E., Gentina, J.C., 1995. Supervision
by the behavior modeling. In SMC’95, IEEE
International Conference on Systems, Man, and
Cybernetics.
Hamani, N., Dangoumau, N., Craye , E., 2005. A
comparative study of mode handling approaches. In
CiE’05, 35th International Conference on Computers
& Industrial Engineering.
Hamani, N., Dangoumau, N., Craye, E., 2006. A
functional modeling approach for Flexible
Manufacturing Systems mode handling. In INCOM'06,
12th IFAC Symposium on Information Control
Problems in Manufacturing. Elsevier Press.
Ndiaye, D., Bigand, M., Corbeel, D., Bourey, J.-P., 2002.
Information system for production engineering. Int. J.
of Computer Integrated Manufacturing, 15(3), 233-
241.
Ranky, P., 1990. Flexible manufacturing cells and systems
in CIM, CIMware Ltd. Guildford, U.K.
Tawegoum, R., Castelain, E., Gentina, J.-C., 1994. Real
time piloting of flexible manufacturing systems.
European J. of Operational Research, 78, 252-261.
Toguyeni, A.K.A., Craye, E., Gentina, J.-C., 1996. A
framework to design a distributed diagnosis in FMS.
In SMC’96, IEEE International Conference on
Systems, Man, and Cybernetics.
Toguyéni, A.K.A., Berruet, P., Craye, E., 2003. Models
and algorithms for failure diagnosis and recovery in
Flexible Manufacturing Systems. Int. J. of Flexible
Manufacturing Systems, 15(1), 57-85.
USING THE OAG TO BUILD A MODEL DEDICATED TO MODE HANDLING OF FMS
287