
TEMPORAL SMOOTHING PARTICLE FILTER FOR VISION BASED
AUTONOMOUS MOBILE ROBOT LOCALIZATION
Walter Nistic
`
o and Matthias Hebbel
Robotics Research Institute (IRF), Technische Universit
¨
at Dortmund, Otto-Hahn-Str. 8, Dortmund, Germany
Keywords:
Particle Filters, Vision Based Localization, Real Time Systems.
Abstract:
Particle filters based on the Sampling Importance Resampling (SIR) algorithm have been extensively and
successfully used in the field of mobile robot localization, especially in the recent extensions (Mixture Monte
Carlo) which sample a percentage of particles directly from the sensor model. However, in the context of
vision based localization for mobile robots, the Markov assumption on which these methods rely is frequently
violated, due to “ghost percepts” and undetected collisions, and this can be troublesome especially when
working with small particle sets, due to limited computational resources and real-time constraints. In this
paper we present an extension of Monte Carlo localization which relaxes the Markov assumption by tracking
and smoothing the changes of the particles’ importance weights over time, and limits the speed at which the
samples are redistributed after a single resampling step. We present the results of experiments conducted on
vision based localization in an indoor environment for a legged-robot, in comparison with state of the art
approaches.
1 INTRODUCTION
Vision-based localization is becoming very popular
for autonomous mobile robots, and particle filters are
a successful technique to integrate visual data for lo-
calization. Due to size, cost and power consumption
limits, many robots use a camera as their only exte-
roceptive sensor; although range finders such as laser
scanners would provide more accurate measurements,
vision can often provide unique features such as land-
marks to speed up global localization.
1.1 The Platform
This work has been developed on the Sony Aibo
ERS-7 robot (Sony Corporation, 2004), which has
been one of the most popular complete standard plat-
forms adopted for robotic applications. The robot is
equipped with a 576MHz 64bit RISC CPU, 64MB of
main memory, and a low-power CMOS camera sen-
sor with a maximum resolution of 416X320 pixel.
The camera is mounted on the robot head, with 3 de-
grees of freedom in the neck; it is severely limited in
terms of resolution, field of view (56.9
◦
horizontally),
and is affected by a significant amount of noise. The
Aibo production has been recently discontinued by
Sony, but several new commercially available robotic
kits are being introduced, such as the humanoid robot
“Nao” from Aldebaran Robotics
1
, with similar char-
acteristics in terms of size and power, often equipped
with embedded RISC CPUs or PDAs and inexpensive
compact flash cameras.
1.2 Related Work
Practical applications of particle filters for mobile
robot localization began with the introduction of the
Sampling Importance Resampling (SIR) filter pro-
posed in (Gordon et al., 1993), (Dellaert et al., 1999)
as an important extension of the Sequential Impor-
tance Sampling (SIS) filter (Geweke, 1989). The SIS
filter requires a huge number of particles to work,
since it does not make an efficient use of them, as
the particle location is not influenced by sensor data
in any way; the resampling step introduced in the SIR
filter acts as a kind of “survival of the fittest” strat-
egy that increases the particle density in the areas of
highest probability of the posterior distribution. How-
ever, in the context of mobile robot localization the
SIR filter suffers of two major problems: difficulty to
1
http://www.aldebaran-robotics.com/
93
Nisticò W. and Hebbel M. (2008).
TEMPORAL SMOOTHING PARTICLE FILTER FOR VISION BASED AUTONOMOUS MOBILE ROBOT LOCALIZATION.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 93-100
DOI: 10.5220/0001497400930100
Copyright
c
SciTePress

recover in the “kidnapped robot” case (i.e. the robot
is moved by an external agent to a new location); and
filter degeneracy, where the filter performance starts
to drop instead of improving as the sensors become
“too” accurate, so that it becomes increasingly diffi-
cult to find particles close enough to the peaks of the
likelihood function. Both problems can be (partially)
eased by increasing the number of particles used, but
this increases the computational cost; a much better
solution has been proposed in (Lenser and Veloso,
2000) which samples a certain percentage of parti-
cles directly from the sensor model (“Sensor Reset-
ting Localization” (SRL)), ensuring that no measure-
ment gets lost due to a lack of particles. A more
formal representation of the sensor resetting idea has
been described in (Thrun et al., 2001) with the “Mix-
ture Monte Carlo” (MMCL) algorithm, where a small
percentage of particles are sampled from the sensor
model and receive importance weights proportional to
the process model, thus (unlike SRL localization) the
belief converges to the true posterior for an infinite
number of samples. In the context of vision based
localization on autonomous mobile robots, in (R
¨
ofer
and J
¨
ungel, 2003) the authors presented an approach
to deal with high levels of noise/uncertainty while us-
ing a small particle set (100 samples). Their approach
keeps track of the individual importance weights of
different landmark classes, and uses this information
to constrain the maximum change of likelihood of the
particle set in a single iteration of the algorithm, thus
easily rejecting outliers in the measured data. The
proposed approach is not formally correct, as we will
show, however it provides surprisingly good results in
practice and it is very popular on the Aibo platform,
thanks also to the availability of its source code
2
.
2 PARTICLE FILTERS
The Particle Filter (Fox et al., 2003) is a non-
parametric implementation of the general Bayes Filter
(Thrun et al., 2005). Given a time series of measure-
ments z
1:t
, control actions u
1:t
and an initial belief
p(x
0
), the Bayes Filter is a recursive algorithm that
calculates the belief or posterior bel(x
t
) at time t of
the state x
t
of a certain process, by integrating sensor
observations z
t
and control actions u
t
over the belief
of the state at time t − 1. The Bayes Filter is based on
the Markov assumption or complete state assumption
which postulates the conditional independence of past
and future data given the current state x
t
. This can
be expressed in terms of conditional independence as
2
http://www.germanteam.org/GT2005.zip
follows:
p(z
t
|x
t
, z
1:t
, u
1:t
) = p(z
t
|x
t
)
p(x
t
|x
t−1
, z
1:t−1
, u
1:t
) = p(x
t
|u
t
, x
t−1
)
(1)
A Particle Filter represents an approximation of the
posterior bel(x
t
) in the form of a set of samples ran-
domly drawn from the posterior itself; such a repre-
sentation has the advantage, compared to closed form
solutions of the Bayes Filter such as the Kalman Fil-
ter (Kalman, 1960), of being able to represent a broad
range of distributions and model non-linear processes,
whereas parametric representations are usually con-
strained to simple functions such as Gaussians. In
the context of robot localization and object tracking,
particle filters are often referred to as Monte Carlo
Localization. Given a set of N samples or parti-
cles χ
t
:= x
1
t
, x
2
t
, . . . , x
N
t
, at time t each particle
represents an hypothesis of the state of the observed
system; in case of robot localization, the state space
is usually represented by the (x, y) cartesian coordi-
nates in the plane, and the heading θ. Obviously, the
higher the number of samples N , the better the ap-
proximation, however (Fox, 2003) has shown how to
dynamically adjust N . In this work we do not con-
sider dynamic adjustments in the number of samples
used, since we are interested in keeping the run-time
of the algorithm approximately constant, due to the
real-time constraints. An estimate of p(x
t
|u
t
, x
t−1
)
Algorithm 1 : SIR Particle Filter.
Require: particle distribution χ
t−1
, control action
u
t
, measurement observation z
t
for i = 1 to N do
1. Process update: update the particles’ state
as the result of the control action u
t
: x
i
t
∼
p(x
t
|u
t
, x
i
t−1
)
2. Measurement update: calculate the particle
importance factors w
i
t
= p(z
t
|x
i
t
) from the latest
observation
Add
x
i
t
, w
i
t
to the temporary set χ
t
end for
3. Resampling: create χ
t
from χ
t
by drawing the
particles x
i
t
in number proportional to their impor-
tance w
i
t
. All the importance factors w
t
in χ
t
are
reset to 1.
is called Process Model, while p(z
t
|x
t
) is known as
Sensor Model. χ
t
before the measurement update
step is a sampled representation of the prior distri-
bution bel(x
t
). If we omit the Resampling step in Al-
gorithm 1we obtain the SIS filter. Under the Markov
assumption, current measurements are statistically in-
dependent from past measurements, as such the im-
portance factors during the Measurement update step
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
94

can be calculated as:
w
i
t
= p(z
t
|x
i
t
) · w
i
t−1
(2)
The SIS filter for localization generally performs
poorly, in fact since the importance weights are up-
dated multiplicatively, a single percept is sufficient to
set the importance of a given particle close to zero. It
has been formally demonstrated that the variance of
the importance weights in the SIS filter can only in-
crease (stochastically) over time (Doucet et al., 2000).
The SIR filter performs much better, because after the
resampling step, the particles of low importance are
discarded while the particles of high importance are
replicated and all the importance weights are reset to
1, i. e. all particles carry the same importance. Con-
sequently the distribution approximates the true pos-
terior bel(x
t
) = ηp(z
t
|x
t
)bel(x
t
).
2.1 Sampling from Observations: The
Kidnapped Robot Problem
The situation when a mobile robot is physically
moved (“teleported”) by an external agent in a new lo-
cation is known as the “Kidnapped Robot” problem.
This situation is challenging because the robot has no
information about such external action and its sensor
and control data is not in accordance with the new
state. The SIR filter as it has been presented has seri-
ous problems dealing with this situation, because it is
unlikely to find a particle in the proximity of the loca-
tion where the robot has been teleported, due to the ef-
fect of resampling which tends to concentrate the par-
ticle distribution in the area of high likelihood of the
posterior at time t − 1, which in this case corresponds
to the robot’s location prior to the teleporting action.
An efficient solution to such problem is to reverse the
Monte Carlo process (“Dual Monte Carlo”) by draw-
ing a certain percentage of the samples directly from
the measurement model instead of the prior belief dis-
tribution :
x
i
t
∼ p(z
t
|x
t
) (3)
and calculate the importance weights from the prior
distribution (integrating the process model):
w
i
t
=
Z
p(x
i
t
|u
t
, x
t−1
)bel(x
t−1
)dx
t−1
(4)
Dual Monte Carlo performs better than normal MCL
with very precise sensors, and can quickly recover
in case the robot is teleported, since the samples are
drawn directly from the last observations. Conversely,
it is extremely sensitive in case of high sensor noise
and performs poorly especially with ghost percepts;
for these reasons, Mixture Monte Carlo uses a small
percentage of samples which are updated using the
Dual MCL approach, and the rest are following the
normal MCL algorithm, thus combining the benefits
of both approaches. The main implementation prob-
lems of the Dual MCL approach is that it is often dif-
ficult to sample from the observation model (Equation
3), when such model does not have a closed form, and
it is both difficult and computationally expensive to
calculate the importance weights from the prior dis-
tribution (Equation 4).
3 TEMPORAL SMOOTHING
PARTICLE FILTER
Particle filters can generally deal efficiently with sen-
sor noise, provided that there is a sufficient amount
of particles (most authors suggest to use at least 1000
particles) and that the measurement model is accurate
enough. However a limit of this approach is that in
practice the Markov assumption can often be violated:
unmodeled dynamics in the environment, such as the
presence of other mobile agents, “ghost” percepts (for
example, echoes in sonar data, or incorrectly classi-
fied objects in a vision system), inaccuracies in the
probabilistic sensor and process model (slippage, col-
lisions), approximation errors due to the sampled rep-
resentation, etc.
3.1 Sensor Smoothing
In (R
¨
ofer and J
¨
ungel, 2003) the authors proposed an
approach which can deal with highly noisy visual
measurements while using a sample set of just 100
particles, which can then be executed in real-time on
severely constrained (in terms of processing power)
mobile robots. The idea is to limit the effect of a sin-
gle measurement (which might be an outlier) on the
particle population; this is achieved by constraining
the measured importance weight ¯w
i
t
for a given parti-
cle at time t to differ at most by a fixed ∆ from the
value that the particle had at time t − 1.
w
i
t
=
(w
i
t−1
+ ∆
up
) if( ¯w
i
t
> w
i
t−1
+ ∆
up
)
(w
i
t−1
− ∆
dn
) if( ¯w
i
t
< w
i
t−1
− ∆
dn
)
¯w
i
t
else
(∆
up
= 0.01, ∆
dn
= 0.005)
(5)
The visual features used for localization are separated
in a set of different percept classes (field lines, bor-
ders and goals are the recognized objects in (R
¨
ofer
and J
¨
ungel, 2003)), the perceived measurements of
different classes are assumed to be statistically inde-
pendent, and each particle carries a different impor-
tance weight per percept class. Consequently, the im-
TEMPORAL SMOOTHING PARTICLE FILTER FOR VISION BASED AUTONOMOUS MOBILE ROBOT
LOCALIZATION
95

portance weight of a particle is calculated as the prod-
uct of the weights associated to each percept class.
From a theoretical point of view, the smoothing per-
formed in Equation 5 is a violation of the Markov as-
sumption, in fact past and current measurements for
objects in the same class are correlated by this up-
date method. This can be seen as an incremental es-
timate of the importance weight of a given particle
with respect to a series of measurements of a certain
object, rather than considering each measurement in-
dependently. For this reason, this method can easily
filter noise in the measurements, as well as limit the
effects of outliers, since it takes a series of consis-
tent measurements to affect significantly the distribu-
tion. However, this approach as presented in (R
¨
ofer
and J
¨
ungel, 2003) has some problems:
1. having ∆
up
6= ∆
dn
introduces an unnecessary
bias in the importance weights;
2. since measurements relative to different objects
are put in the same class, and the particles keep
their “memory” indefinitely, this mechanism in-
correctly correlates measurements which should
be independent.
While fixing the first problem is trivial, the same is not
true about the second; the correct solution would be
to assign a different percept class to each perceived
object, so that they can be treated as statistically in-
dependent. This however is not always possible, be-
cause in some cases the robot is observing different
objects which are undistinguishable, like walls in vi-
sion based localization, or range measurements with
laser scanners. Thus, here we introduce an “aging
law” which fades out the memory of past measure-
ments in the importance weights, thus reducing the in-
correct correlations among percepts of the same class.
This corresponds to an assumption of temporal co-
herence of a series of measurements, i. e. we expect
“bursts” of measurements relative to a certain object
to appear for a short time. So, if we define a set Γ of
percept classes, let w
i,j
t
be the importance weight for
the percept class j ∈ Γ relative to the i-th particle at
time t, α
j
∈ [0..1] an aging factor for class j, then the
result of the aging process ˆw
i,j
t
can be calculated as:
ˆw
i,j
t
= w
i,j
t
+ (1 − w
i,j
t
) · α
j
(6)
This function asymptotically fades an importance fac-
tor toward 1 (i. e. that percept class does not affect the
global importance factor of that particle), with a speed
controlled by the parameter α
j
, which can be set ac-
cording to the frequency of independent observations
of a given percept class. For α tending to 0, the par-
ticles keep “memory” of old percepts for a long time,
while for α tending to 1 the particle weights are re-
set in each iteration like in the SIR filter. This is also
beneficial in case a series of past measurements for a
given class resulted in a very low weight, which with-
out aging would affect negatively the global weight
of the particle, regardless of the values of the other
percept classes. Finally, after the aging step (Equa-
tion 6), given a ¯w
i,j
t
calculated from the measurement
model, we can apply the temporal smoothing step:
w
i,j
t
=
( ˆw
i,j
t−1
+ ∆
j
) if( ¯w
i,j
t
> ˆw
i,j
t−1
+ ∆
j
)
( ˆw
i,j
t−1
− ∆
j
) if( ¯w
i,j
t
< ˆw
i,j
t−1
− ∆
j
)
¯w
i,j
t
else
w
i
t
=
Y
j∈Γ
w
i,j
t
(7)
3.2 “lazy” Resampling
The main problem of the approach described in
(R
¨
ofer and J
¨
ungel, 2003) is the resampling step: par-
ticles are copied in the new distribution χ with a fre-
quency proportional to their importance weight w
i
t
,
as in the Step 3 of Algorithm 1, but the weights w
i,j
t
are not reset to 1 afterward, this because otherwise it
would not be possible to use them to filter the mea-
surements at the following iterations of the algorithm.
So, supposing that a particle with importance w
i
t
is
copied n
i
> 1 times in the target distribution χ, the
probability density in that location will increase by a
factor of n
i
. Consequently, after the resampling step
the particle distribution does not approximate the true
posterior anymore: the probability density will artifi-
cially increase in areas of high likelihood, while it will
further decrease in areas of low likelihood. The re-
sult is that this filter converges very quickly and tends
to focus most of the particles around the main peak
of the probability distribution; in practice the filter
works very well as long as the noise can be filtered
by its sensor smoothing mechanism, but when there
is a high level of ambiguity in the sensor data, for ex-
ample if no unique landmark is observed in a long
time, then the particles will start to quickly oscillate
among different peaks of the true posterior distribu-
tion, rather than assume a multi-modal distribution.
This problem can be fixed however, if we know the
number of times n
i
that a certain particle i has been
copied. This can be used to normalize the weights in
the target distribution, so that it again approximates
the posterior:
˜w
i
t
=
w
i
t
n
i
t
⇒
Q
j∈Γ
w
i,j
t
Q
j∈Γ
ν
i
t
⇒
Y
j∈Γ
w
i,j
t
ν
i
t
ν
i
t
=
c
q
n
i
t
; c = kΓk
(8)
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
96

where, given n
i
and c (the number of percept classes)
we can normalize the global weight of the particle ˜w
i
t
dividing its importance weights by the coefficient ν
i
t
.
As the basis for our new resampling algorithm, we
use the low variance sampler (Thrun et al., 2005).
The low variance sampler has several advantages over
Algorithm 2 : Low Variance Sampling.
Require: proposal particle distribution ¯χ
t
, impor-
tance weights W
t
, number of particles N
χ
t
= ∅
r = rand(0; N
−1
)
c = w
1
t
i = 1
for m = 1 to N do
U = r + (m − 1) · N
−1
while U > c do
i = i + 1
c = c + w
i
t
end while
add x
i
t
to χ
t
end for
return target distribution χ
t
the independent random sampler described in the ba-
sic SIR filter algorithm: it has O(N ) complexity (in-
stead of O(N log(N ))), it guarantees that if all parti-
cles have the same importance, χ
t
is the same as ¯χ
t
,
and most importantly for us, it covers the set of sam-
ples systematically, making it much easier to track the
values n
i
to use for normalization. At this point, we
can introduce a new technique, that here we will call
“lazy resampling”, to enforce temporal coherence in
the particle distribution: we can clip the number of
new samples in the target distribution χ which can be
generated from a single particle in the proposal dis-
tribution ¯χ to be at most a chosen ¯n
max
∈ [1..N ].
The idea is to reduce the effect of a single resampling
step on the particle distribution: if a robot is well lo-
calized and it is not teleported, we would expect that
the peaks of the posterior distribution at time t are
close to the position they had at time t − 1, factoring
in the odometry data in the process update step. Es-
pecially when drawing some samples from the mea-
surement model, as in the Sensor Resetting / Mixture
Monte Carlo approaches described, a few bad mea-
surements would move many particles away from the
area of high likelihood, degrading the performance of
the filter; by setting a limit to the number of times
that a single particle can be copied as a consequence
of resampling, we are reducing the effects of outliers
on the particle distribution. The downside is that, in
case the robot is really teleported, our filter would be
slower in relocating most of the particles in the new
area of high likelihood: the robot would still relocate
its estimate quickly, because of the update in the par-
ticle importance weights, but there would be initially
less resolution in the area where the robot has been
teleported. Thus, it is necessary to set a value of ¯n
max
as a compromise dependent on the frequency of robot
teleports and the amount of sensor noise and ambigu-
ity. For ¯n
max
= 1, a particle in ¯χ is copied unaltered
in χ, as such the SIS filter can be seen as a special case
of our lazy resampling; at the other end of the spec-
trum, setting ¯n
max
= N results in no limitations in
the effects of resampling, so our filter behaves exactly
like a SIR filter. Algorithm 3 describes a possible im-
plementation, r is used to calculate how many times a
certain particle should be copied in the target distribu-
tion based on its importance weight; such number is
clipped to a maximum resample limit of ¯n
max
. Par-
ticles of low weight (n < 1) are copied in the target
distribution starting from the end of the list (indexed
by j), so that they can be overwritten by the more im-
portant particles, which are copied starting from the
beginning of the list (indexed by i).
Algorithm 3 : “Lazy” Resampling.
Require: proposal particle distribution ¯χ
t
, impor-
tance weights W
t
, number of particles N , resample
limit ¯n
max
χ
t
= ∅
i = 1
j = N
r =
N
P
i
w
i
t
for m = 1 to N do
n = min(br · w
m
t
c; ¯n
max
)
if n > 0 then
normalize ˜w
m
t
=
w
m
t
n
for z = 1 to n do
add x
m
t
, ˜w
m
t
to
D
χ
t
,
˜
W
t
E
in position i
i = i + 1
end for
else
if j > i then
add x
m
t
, w
m
t
to
D
χ
t
,
˜
W
t
E
in position j
j = j − 1
end if
end if
end for
return target distribution
D
χ
t
,
˜
W
t
E
TEMPORAL SMOOTHING PARTICLE FILTER FOR VISION BASED AUTONOMOUS MOBILE ROBOT
LOCALIZATION
97
4 EXPERIMENTS AND RESULTS
In the following experiments, we will evaluate the
performance of our new approach (from now on
referred to as Temporal Smoothing Monte Carlo
“TSMCL”) which uses our sensor smoothing with ag-
ing (Equations 6,7) and the lazy resampling strategy
described in Algorithm 3. We compare it with a SIR
filter with Sensor Resetting, and the approach de-
scribed in (R
¨
ofer and J
¨
ungel, 2003) (here for conve-
nience referred to as Sensor Smoothing Monte Carlo
“SSMCL”).
4.1 Test Environment
The robot is placed in a soccer field whose size is
6m×4m, where it can recognize 4 unique landmarks:
2 goals (1 yellow, 1 blue) and 2 cylindrical beacons
(yellow on blue, and blue on yellow). The position
of the landmarks on the map is known to the robot.
Additionally, the robot can recognize non unique fea-
tures such as the white lines on the field, and the inter-
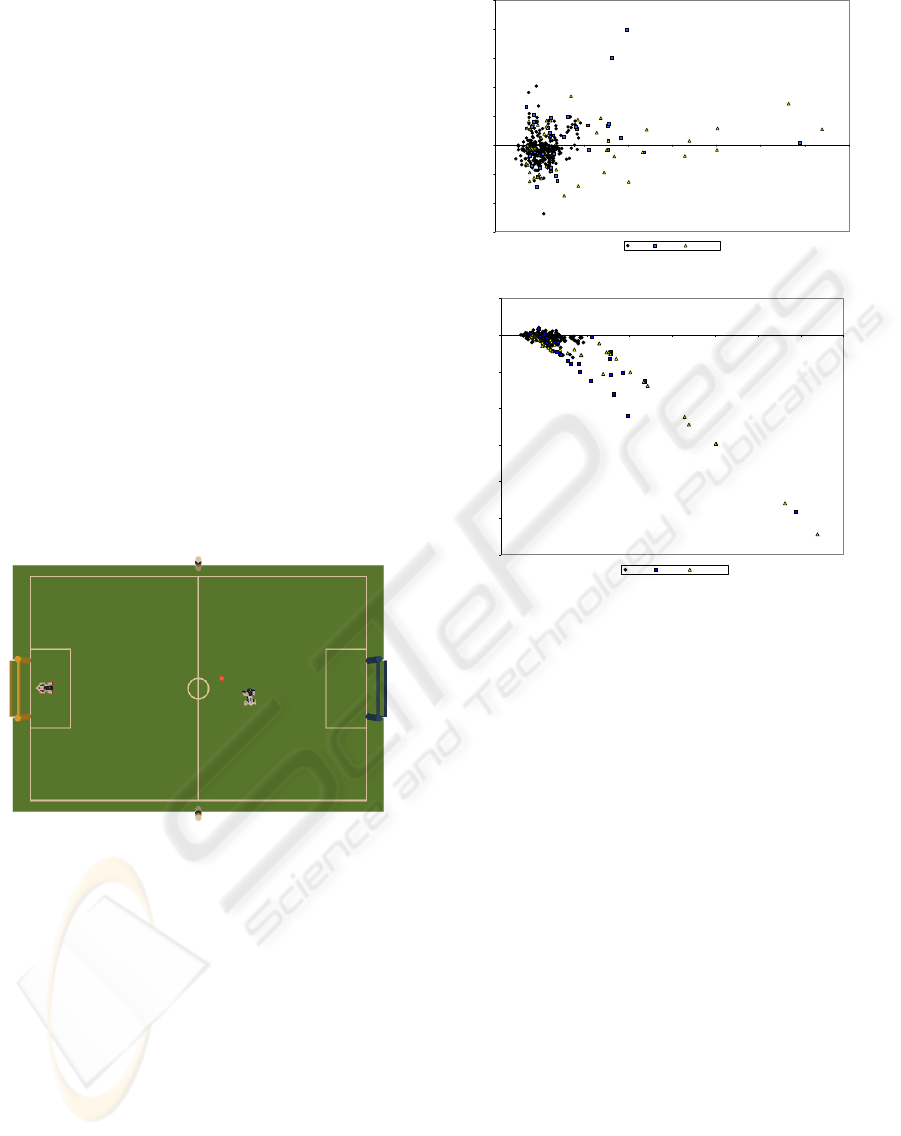
sections where the lines meet (see Figure 1). Since the
Figure 1: Test environment: a yellow and a blue goal, two
colored beacons (on the middle line), two robots and an or-
ange ball.
environment is color coded, the vision system, simi-
lar to the approach described in (Nistic
`
o and R
¨
ofer,
2006), uses color based image segmentation. The vi-
sion and localization systems run at 30 frames per sec-
ond.
As can be seen in Figure 2, the measurement error
is high (especially the measured distance error grows
almost exponentially with the distance to the observed
object), due to the low resolution of the camera and
the fact that the camera pose in space can only be
roughly estimated. In fact the camera is mounted on
the head of the robot, it has 3 degrees of freedom and
due to the narrow field of view, it has to constantly
scan around at high angular velocity. Moreover, the
-30
-20
-10
0
10
20
30
40
50
0 2000 4000 6000 8000 10000 12000 14000 16000
Beacons Blue Goal Yellow Goal
(a) Bearing Error
-12000
-10000
-8000
-6000
-4000
-2000
0
2000
0 2000 4000 6000 8000 10000 12000 14000 16000
Beacons Blue Goal Yellow Goal
(b) Distance Error
Figure 2: Landmark Measurement error. The bearing (de-
grees) and distance (mm) errors are plotted as a function of
the perceived distance.
height of the neck on which the camera is mounted is
not constant since the robot uses legged locomotion,
and it can only be approximately estimated through
kinematic calculations from the servos’ encoders in
the robot legs. For these reasons our sensor model
calculates the measurement error in terms of hori-
zontal angle (bearing) and vertical angle (depression)
to the observed object. This has the advantage that,
while the distance error grows more than linearly with
the real distance to the object, the vertical angle er-
ror variance is approximately constant. We assume
the horizontal and vertical angle error components to
be independent, and use gaussian likelihood functions
to model each component, with different constants
σ
j
horizontal
, σ
j
vertical
, j ∈ Γ for each percept class.
Field lines and their intersections (crossings) due to
their small size can only be recognized reliably up to
a maximum distance of approximately 800mm; for
these non-unique features we adopt a closest point
matching model (with pre-computed lookup tables)
as described in (R
¨
ofer and J
¨
ungel, 2003). Due to the
different measurement errors (see Table 1) and fre-
quency of detection, we distinguish our percepts in 3
different classes: Γ = {Beacons, Goals, Lines}.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
98
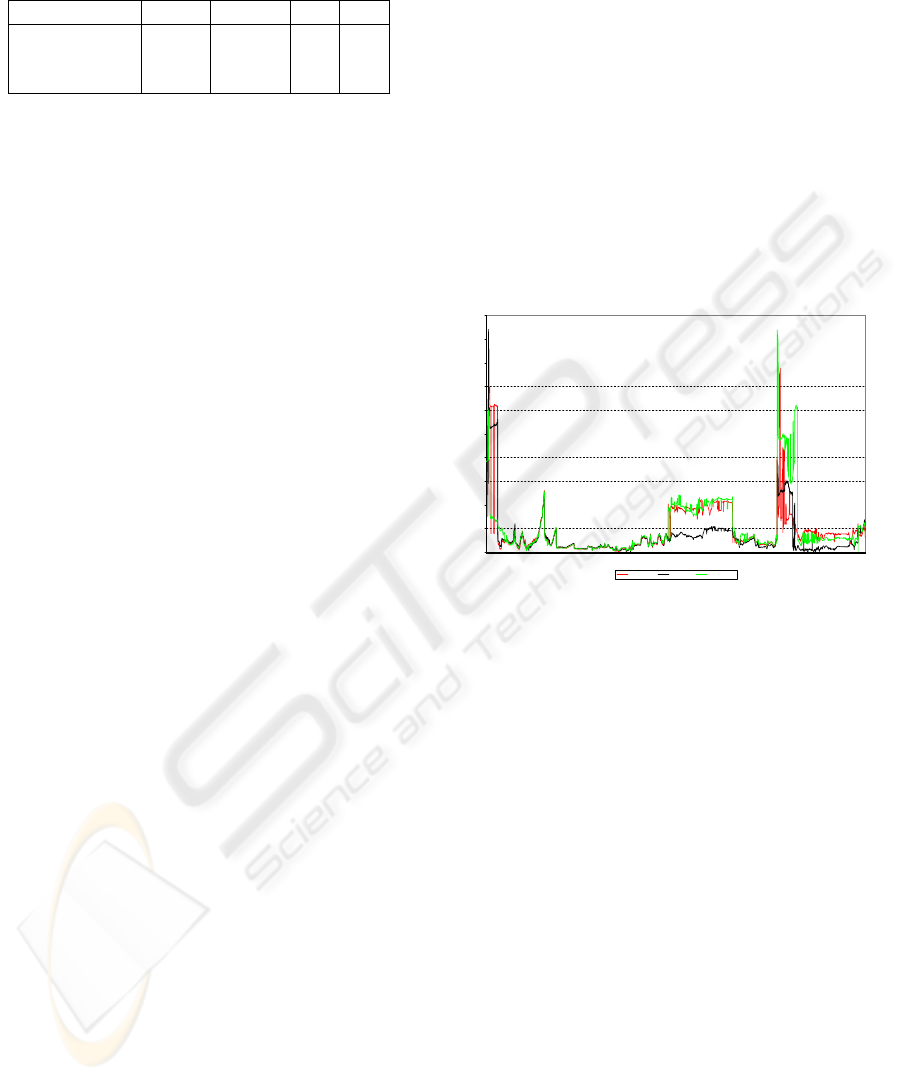
Table 1: Measurement error. ρ represents the distance error,
in expressed in mm; α the bearing error, in deg..
Percept Class µ
ρ
σ
ρ
µ
α
σ
α
Beacons 162.7 178.5 3.2 3.1
Goals 708.5 1294.6 4.6 4.8
Lines 122.6 215.8 3.1 3.5
All three localization algorithms use overall 100
particles, draw a small percentage of them directly
from observations, and are executed in parallel in real-
time on our test platform. The locations for such sam-
ples are calculated from landmarks via triangulation
or using two bearings and two distances; for this pur-
pose, the location of seen landmarks is retained for
5 seconds and updated using odometry information.
Additionally, line crossings are classified as T-shaped
or L-shaped, and samples are drawn from all possi-
ble locations which match the seen shape (8 at most,
for L-shaped crossings, hence we use a mixture with
8% of particles drawn from observations), and two
further possible poses are found if the center circle is
seen. To provide ground truth to evaluate the localiza-
tion performance, we use an external vision system
based on a ceiling-mounted camera which is able to
track the robot position at 25 frames per second with
a maximum error of 40mm (position) and 2
◦
degrees
(heading). The process model updates the particle
positions based on odometry data which is provided
by the robot’s motion module; the odometry error is
modeled as a bi-dimensional gaussian with the ma-
jor axis parallel to the direction of movement, and an
independent gaussian represents the heading error.
4.2 Experiments
In the static localization case, with the robot hav-
ing unlimited time to reach a specified position on
the field, all three approaches are able to localize the
robot with a position error below 7 cm and heading
error below 3 degrees, and in this situation it is not
possible to make an analysis of the relative perfor-
mance, due to measurement errors in the ceiling cam-
era system providing ground truth and the fluctuations
derived from the randomized nature of the localiza-
tion algorithms employed. So in the following exper-
iments, we will analyze the accuracy of localization
while the robot runs around the field: in the first half
of each experiment the robot will be allowed to look
around to see unique landmarks, in the second half it
will be chasing a ball looking only at it, hence see-
ing landmarks only occasionally, having to rely on
non-unique features such as lines and crossings for
localization. In the first experiment, we want to il-
lustrate the effects of our lazy resampling, by com-
paring the performance of our algorithm for different
values of the resample limit ¯n
max
: 8 (the experimen-
tally derived optimum for our application), 15 and
30 (for all practical purposes, equivalent to “unlim-
ited”, given a set of 100 particles). As can be seen
in Figure 3, all three versions localize about at the
same time (≈ 180 frames or 6 seconds), then they
perform equally well, as long as the robot receives
reasonably good percepts. However, in the situations
where the robot looks only at the ball for a long time,
the version with ¯n
max
= 8 performs much better, be-
ing more effective in smoothing the noise and resolv-
ing ambiguities by keeping more particles in the areas
where the robot was previously localized. In the sec-
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
1 206 411 616 821 1026 1231 1436 1641 1846 2051 2256 2461 2666 2871 3076 3281 3486 3691 3896 4101 4306 4511 4716 4921 5126 5331 5536 5741 5946
15 Particles 8 Particles 30 Particles
Figure 3: Resample limit comparison (Test 1). x-axis: time
(frames); y-axis: position error. At frames 2900-3950 and
4700-5100 the scarcity of unique features and the odometry
errors make the localization jump to a wrong location.
ond experiment, we compare our TSMCL algorithm
with ¯n
max
= 8 to the state of the art approaches. In
the first half of the experiment, all systems perform
equally well, with TSMCL and SIR nearly identical
and SSMCL slightly worse but within the limits due
to random factors. When the robot starts to chase
the ball however (after frame 3000), SIR and SSMCL
start to oscillate much more (Figure 4). Our third test
is similar to the second, but it represents a worse sce-
nario since this time the beacons (which are the best
landmark, in terms of measurement error and ease of
detection) are removed. The results presented in Fig-
ure 5 show our approach clearly outperforming the
others. The run-time of all 3 algorithms is 3−5ms per
frame, depending on the number and type of percepts
seen. We could not measure significant differences in
the time taken to globally localize and recover from
kidnapping (2 − 6s in all cases).
TEMPORAL SMOOTHING PARTICLE FILTER FOR VISION BASED AUTONOMOUS MOBILE ROBOT
LOCALIZATION
99
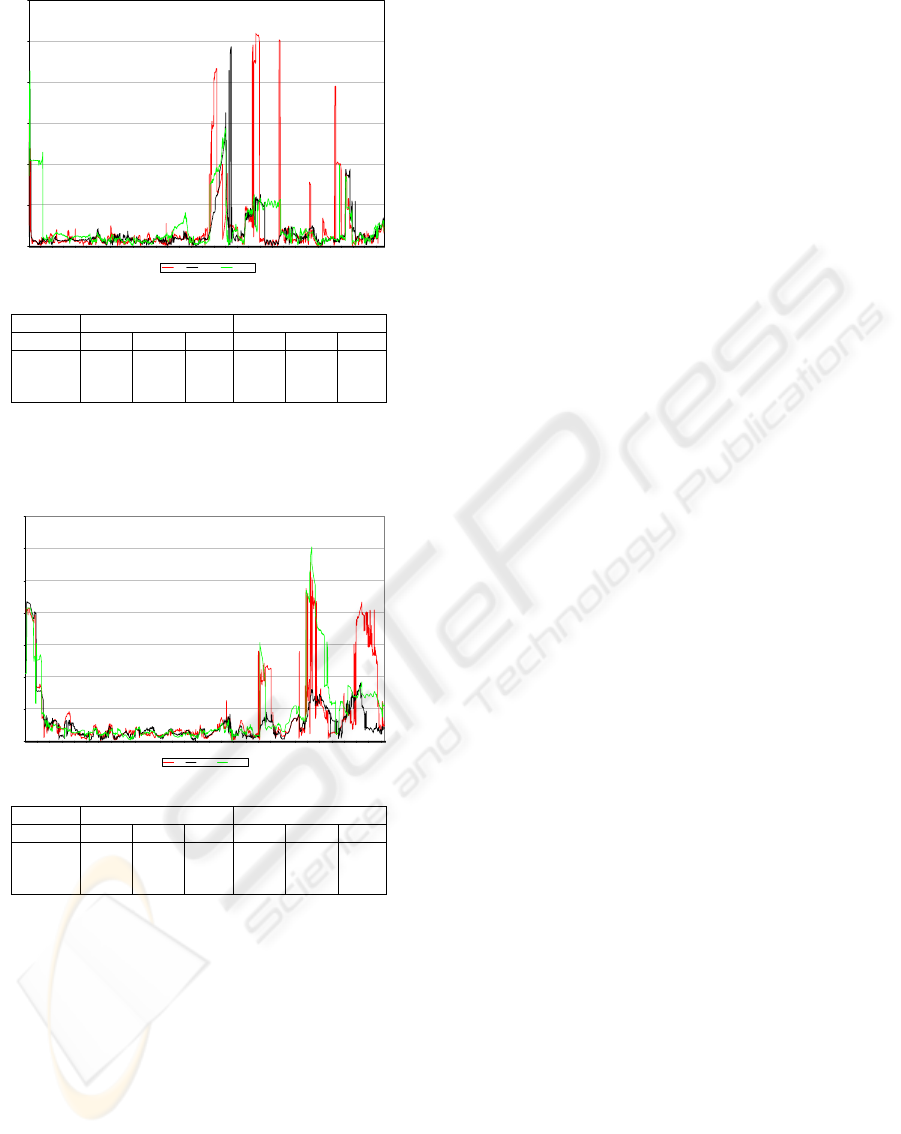
0
1000
2000
3000
4000
5000
6000
1 228 455 682 909 1136 1363 1590 1817 2044 2271 2498 2725 2952 3179 3406 3633 3860 4087 4314 4541 4768 4995 5222 5449 5676 5903 6130
SIR TSMCL SSMCL
(a)
First Half Overall
µ σ max µ σ max
TSMCL 144.8 62.8 430 323.6 503.0 4864
SSMCL 201.9 130.3 813 444.1 553.1 2875
SIR 146.2 76.1 548 436.7 897.1 5195
(b)
Figure 4: Localization algorithm comparison (Test 2). x-
axis: time (frames); y-axis: position error.
0
1000
2000
3000
4000
5000
6000
7000
1 197 393 589 785 981 1177 1373 1569 1765 1961 2157 2353 2549 2745 2941 3137 3333 3529 3725 3921 4117 4313 4509 4705 4901 5097 5293 5489 5685
SIR TSMCL SSMCL
(a)
First Half Overall
µ σ max µ σ max
TSMCL 277.5 160.1 847 432.7 355.0 1811
SSMCL 276.3 128.6 867 745.8 998.1 6051
SIR 294.2 169.0 1261 706.9 993.7 5567
(b)
Figure 5: Localization algorithm comparison (Test 3). x-
axis: time (frames); y-axis: position error.
5 FUTURE WORK
We have presented an extension of Monte Carlo
Localization which exploits temporal smoothing to
improve localization accuracy in presence of high
amounts of noise and sensor ambiguity. In the fu-
ture we would like to apply our algorithm to multi-
object tracking, where its use of temporal coherence
could allow it to “keep memory” of multiple modes
in the distribution more effectively than normal parti-
cle filters, making it a good candidate to compete with
banks of multiple filters with degrees of association.
REFERENCES
Dellaert, F., Fox, D., Burgard, W., and Thrun, S. (1999).
Monte carlo localization for mobile robots. In IEEE
International Conference on Robotics and Automation
(ICRA99).
Doucet, A., Godsill, S., and Andrieu, C. (2000). On se-
quential monte carlo sampling methods for bayesian
filtering. Statistics and Computing, 10:197–208.
Fox, D. (2003). Adapting the sample size in particle filters
through kld-sampling. I. J. Robotic Res., 22(12):985–
1004.
Fox, D., Hightower, J., Liao, L., Schulz, D., and Borriello,
G. (2003). Bayesian Filtering for Location Estimation.
PERVASIVE computing, pages 10–19.
Geweke, J. (1989). Bayesian inference in econometric
models using monte carlo integration. Econometrica,
57(6):1317–39.
Gordon, N. J., Salmond, D. J., and Smith, A. F. M. (1993).
Novel approach to nonlinear/non-gaussian bayesian
state estimation. Radar and Signal Processing, IEE
Proceedings F, 140(2):107–113.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. Transactions of the ASME -
Journal of Basic Engineering, 82:35–45.
Lenser, S. and Veloso, M. (2000). Sensor resetting local-
ization for poorly modelled mobile robots. In Pro-
ceedings of the IEEE International Conference on
Robotics and Automation, 2000.
Nistic
`
o, W. and R
¨
ofer, T. (2006). Improving percept reli-
ability in the sony four-legged league. In RoboCup
2005: Robot Soccer World Cup IX, Lecture Notes in
Artificial Intelligence, pages 545–552. Springer.
R
¨
ofer, T. and J
¨
ungel, M. (2003). Vision-Based Fast and
Reactive Monte-Carlo Localization. In Proceedings of
the 2003 IEEE International Conference on Robotics
and Automation, ICRA 2003, September 14-19, 2003,
Taipei, Taiwan, pages 856–861. IEEE.
Sony Corporation (2004). OPEN-R SDK Model Informa-
tion for ERS-7. Sony Corporation.
Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic
Robotics. Number ISBN 0-262-20162-3. MIT Press.
Thrun, S., Fox, D., Burgard, W., and Dellaert, F. (2001).
Robust monte carlo localization for mobile robots. Ar-
tificial Intelligence, 128(1-2):99–141.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
100
