
AN EFFICIENT INFORMATION EXCHANGE STRATEGY IN A
DISTRIBUTED COMPUTING SYSTEM
Application to the CARP
Kamel Belkhelladi
1,2
, Pierre Chauvet
1,2
and Arnaud Schaal
2
1
LISA, Universit´e d’Angers, 62, avenue Notre Dame du Lac, 49000 Angers, France
2
CREAM, Universit´e Catholique de l’Ouest, 44-46, rue Rabelais, 49008 Angers, France
Keywords:
Capacitated Arc Routing Problem, Information exchange strategy, Distributed computing, Agents.
Abstract:
Distributed computation models have been widely used to enhance the performance of traditional evolutionary
algorithms, and have been implemented on parallel computers to speed up the computation. In this paper,
we introduce a multi-agent model conceived as a conceptual and practical framework for distributed genetic
algorithms used both to reduce execution time and get closer to optimal solutions. Instead of using expensive
parallel computing facilities, our distributed model is implemented on easily available networked personal
computers (PCs). In order to show that the parallel co-evolution of different sub-populations may lead to an
efficient search strategy, we design a new information exchange strategy based on different dynamic migration
window methods and a selective migration model. To evaluate the proposed approach, different kinds of
experiments have been conducted on an extended set of Capacitated Arc Routing Problem(CARP). Obtained
results are useful for optimization practitioners and show the efficiency of our approach.
1 INTRODUCTION
Genetic Algorithms, a special class of Evolutionary
Algorithms (EAs), are proven to be successful in a
wild range of applications, especially in cases of op-
timization. In order to solve more difficult problems,
two inherent features of EAs, premature convergence
and computation time must be improved. To over-
come the two problems, the idea of parallelizing EAs
has been proposed by different researchers, and it
has been proven to be a promising method (Cant`u-
Paz, 2000). Conceptually, the parallelism is to di-
vide a big population in a sequential EA into multiple
smaller sub-populations that are distributed to sepa-
rate processors and can then be evaluated simultane-
ously. According to the sub-population size, the par-
allel EAs are categorized into two types: coarse-grain
and fine-grain, and they are usually implemented on
distributed memory and massively parallel comput-
ers, respectively. All though parallel computers can
speed up EAs, they are not easily available and it is
very expensive to upgrade their processing power and
memory. A promising alternative without expensive
hardware facilities is to construct the parallel evolu-
tionary computation (EC) framework on a set of net-
worked personal computers.
To make the parallel EAs more realistic, we pro-
pose in this paper a mobile agent-based methodol-
ogy to support parallelism on networked computers
in a flexible and adaptive way. In addition, we de-
sign a new information exchange strategy. The idea
is that an EA periodically selects some promising in-
dividuals from each sub-population and sends them
to other sub-populations, according to certain criteria.
To evaluate the proposed approach, different kinds of
experiments have been conducted on an extended set
of Capacitated Arc Routing Problem (CARP) and the
obtained results show the promise and efficiency of
our approach.
2 THE CARP
The Capacitated Arc Routing Problem (CARP) is a
vehicle routing problem raised by applications like ur-
ban waste collection, snow plowing, sweeping, grit-
ting, etc. It is defined on an undirected network
G=(V,E), with a set V of n nodes and a set E of m
edges. A fleet of identical vehicles with capacity W is
based at a depot node s. Each edge e can be traversed
342
Belkhelladi K., Chauvet P. and Schaal A. (2008).
AN EFFICIENT INFORMATION EXCHANGE STRATEGY IN A DISTRIBUTED COMPUTING SYSTEM - Application to the CARP.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 342-346
DOI: 10.5220/0001497103420346
Copyright
c
SciTePress

any number of times, each time with a cost c
e
, and
has a non-negativedemand q
e
. All costs and demands
are integers. The τ edges with non-zero demands are
called required edges or tasks and require service by a
vehicle. The goal is to determine a set of vehicle trips
of minimum total cost, such that each trip starts and
ends at the depot, each required edge is serviced by
one single trip, and the total demand handled by any
vehicle does not exceed W.
Since the CARP is NP-hard, large scale instances
must be solved in practice using heuristics. Among
fast constructive methods, one can cite Path-Scanning
(Golden et al., 1983) and Ulusoy’s splitting technique
(Ulusoy, 1985). Available meta-heuristics are very
recent and include tabu search methods (Belenguer
and Benavent, 2003; Hertz et al., 2000), guided local
search (Beullens et al., 2003) and genetic algorithm
(Lacomme et al., 2001). All these heuristics algo-
rithms can be evaluated through lower bounds (Am-
berg and Voß, 2002).
3 AGENT-BASED APPROACH
The DGA-MAS
1
developed in this work uses several
components of the genetic algorithm algorithm pro-
posed by (Lacomme et al., 2001) for the CARP. The
common parts are described below:
Solution Encoding: The network is coded as a sym-
metric digraph, in which each edge is replaced by two
opposite arcs. A chromosome is an ordered list of the
τ tasks, in which each task may appear as one of two
directions. The implicit shortest paths are assumed
between successive tasks. The chromosome does not
include trip delimiters and can be viewed as a giant
trip for an incapacitated vehicle. A procedure Split
optimally partitions (subject to the sequence) the gi-
ant trip into feasible trips. The fitness function of the
genetic algorithm (GA) is the total cost of the result-
ing CARP solution.
Initialization: The global population P of chro-
mosomes is initialized with the solutions of the
two CARP heuristics cited in introduction (PS and
UH)(Golden et al., 1983; Ulusoy, 1985), completed
by random permutations. The distributed genetic
algorithm (DGA) forbids clones (identical chromo-
somes).
Selection and Crossover: At each iteration, two par-
ents are selected by a biased roulette wheel (Gold-
berg, 1989). Three crossovers were defined for
the giant trip representation, LOX (Linear Order
Crossover), a modified version of the classical order
1
Distributed Genetic Algorithm using Multi-agent Sys-
tem
crossover OX and X1 (crossing in a point).
Mutation: Several mutation operators have been pro-
posed for the CARP, such as inversion, insertion, dis-
placement (MOVE), and reciprocal exchange muta-
tion (SWAP). Reciprocal exchange mutation selects
two positions at random and swaps the tasks on these
positions.
Several researchers are trying to compare the per-
formance of using coarse-grain and fine-grain mod-
els to parallelize genetic algorithms. Some prefer
fine-grain models but others favor coarse-grain ones
(Cant`u-Paz, 2000). As our goal is to develop a
distributed genetic framework without using a pow-
erful connection machine, we choose to implement
a coarse-grain model on a set of networked PCs.
By using the concept of coarse-grained paralleliza-
tion, the population is divided into a few large sub-
populations. These sub-populations evolve indepen-
dently and concurrently on different processors. After
a predefined period of time, some selected individuals
are exchanged via a migration process.
Our distributed genetic algorithms with multiple
sub-populations uses the master-slave (Luque et al.,
2005) multi-agent model for the CARP. The inter-
connection topology is logically a star, with the mas-
ter in the center. Our new migration process is
based on different dynamic migration window meth-
ods (Kim, 2002) and the selective migration model
(Eldos, 2006).
In the master-slave multi-agent model, the master
agent maintains the lists of partial results that are sent
from slaves. At first, the master agent generates the
population and divides them into sub-populations. It
sends them to slave agents. The slaves execute a con-
ventional genetic algorithm on their sub-population:
fitness evaluation, selection, crossover, mutation and
periodically return their best partial results to the mas-
ter agent. Pseudo-code of the conventional genetic
algorithm is shown in section 3.1. The subroutine Mi-
gration is an extension to a general coarse-grained
model. The master stores the partial results in lists.
Then, the master agent searches the lists and selects
two slaves that have bad partial results and sends the
migration window size to selected slaves. The se-
lected slaves exchange individuals according to the
migration window methods. However, in the pro-
posed model, individuals are screened and examined
at both the source and the destination to qualify for
migration. The source gives or denies a visa based on
local qualification criteria and the destination grants
or denies a residency based on local qualification cri-
teria. The simplest form of qualification criteria is
through the individual’s relative fitness. Every in-
dividual in a very sub-population is ranked locally;
AN EFFICIENT INFORMATION EXCHANGE STRATEGY IN A DISTRIBUTED COMPUTING SYSTEM -
Application to the CARP
343

an individual qualifies for a visa at the source sub-
population if its rank is within a range, typically the
middle class. On the destination sub-population, an
immigrant is accepted as a new member of the popu-
lation if its rank is better than a threshold set by that
receiving sub-population.
3.1 The Algorithm
The Pseudo-code of the algorithm in each slave Agent
is described as below:
initialize the population, P
while generation < max_generation begin
evaluate P
select P1’ from P using roulette
wheel selection
select parents randomly from P1’
apply genetic operators to create
the rest of the new population, P2’
merge P1’ and P2’ to P’
replace P with P’
if an interval of K generations is reached
Migration
end
generation = generation + 1
end
subroutine Migration
begin
Pick a random number (1 - pop_size)
to nominate
an immigrant X
If the rank of X is within limits then
Send X to the Master
Mark X as "dead" to be killed
end
If an immigrant Y is received then
If the rank of Y exceeds threshold
Add to the population
Update Fitness and Ranking
Pick a random number (1 - pop_size)
to nominate a victim V
Discard the victim V
end
end
end
4 EXPERIMENTS AND RESULTS
Following our computational experiments and the
agent’s methodology, we conducted two series of ex-
periments to compare the corresponding performance
for genetic computation with and without individ-
ual’s exchange. The first series examines whether the
parallel implementation can improve search quality.
The second series of experiments evaluates the per-
formance of using Multi-agent and the individuals ex-
change strategies in order to exploit the computational
power of multiple machines.
Both the pure Parallel Genetic Algorithm (PGA)
and the Distributed Genetic Algorithm (DGA-MAS),
including the multi-agent strategies, are implemented
on a network of PCs, connected with a 100Mbit/sec
Ethernet. In the experiments, we arranged eight net-
worked computers running Suse Linux operating sys-
tem as a distributed computing environment to sup-
port our Multi-agent system.
One computer played the role of ”master” and
ran the multi-agent platform. Once the platform was
activated, the master agent instantiated other agents
(slave agents) and sent each one towards a machine
in the network. Each machine in this framework
had a slave agent to take care of the computation for
each sub-population. Also, the master agent allowed
activation of the communication phase described in
Section 3 for exchanging individuals among sub-
populations.
In the experiments, we use three crossover types
(LOX, OX, X1) and two mutation types (MOVE,
SWAP). Sevenvalues for crossover rate are used rang-
ing from 0.2 to 0.7 in increments of 0.1. Also, seven
mutation rates are allowed varying from 0.1 to 0.4
in increments of 0.05. Our results are obtained with
small sub-populations of 30 solutions. Clones (iden-
tical solutions) are forbidden in each sub-population,
to have a better dispersion of solutions and to dimin-
ish the risk of premature convergence. The number
of generations is fixed to 5000 for all slave agents.
The migration interval is 500 generations. Whenever
migration occurs, the dynamic migration window size
varies at random from 1 to θ. The θ value is generated
at random within 20% of the sub-population size. The
threshold value is fixed to the mean fitness of the sub-
population.
These tests are done on a standard set of undi-
rected instances in which all edges are required. Table
1 contain 23 instances from (DeArmon, 1981) with 7
to 27 nodes and 11 to 55 edges. All these files can be
obtained at http://www.uv.es/∼belengue/carp.html.
In the Table 1, Pb gives the instance number and
N,M the numbers of nodes and edges. LBB is a lower
bound from (Belenguer and Benavent, 2003). TS is
the result of Carpet (Hertz et al., 2000) with the pa-
rameter setting yielding the best results on average
(the same setting for all instances). Best gives the
best solution published, generally obtained by Car-
pet with various parameter settings. GA is the so-
lution of GA from (Lacomme et al., 2001). Our re-
sults are shown in the pure parallel genetic algorithm
(PGA) and the distributed genetic algorithm includ-
ing the Multi-agent strategy (DGA) columns.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
344
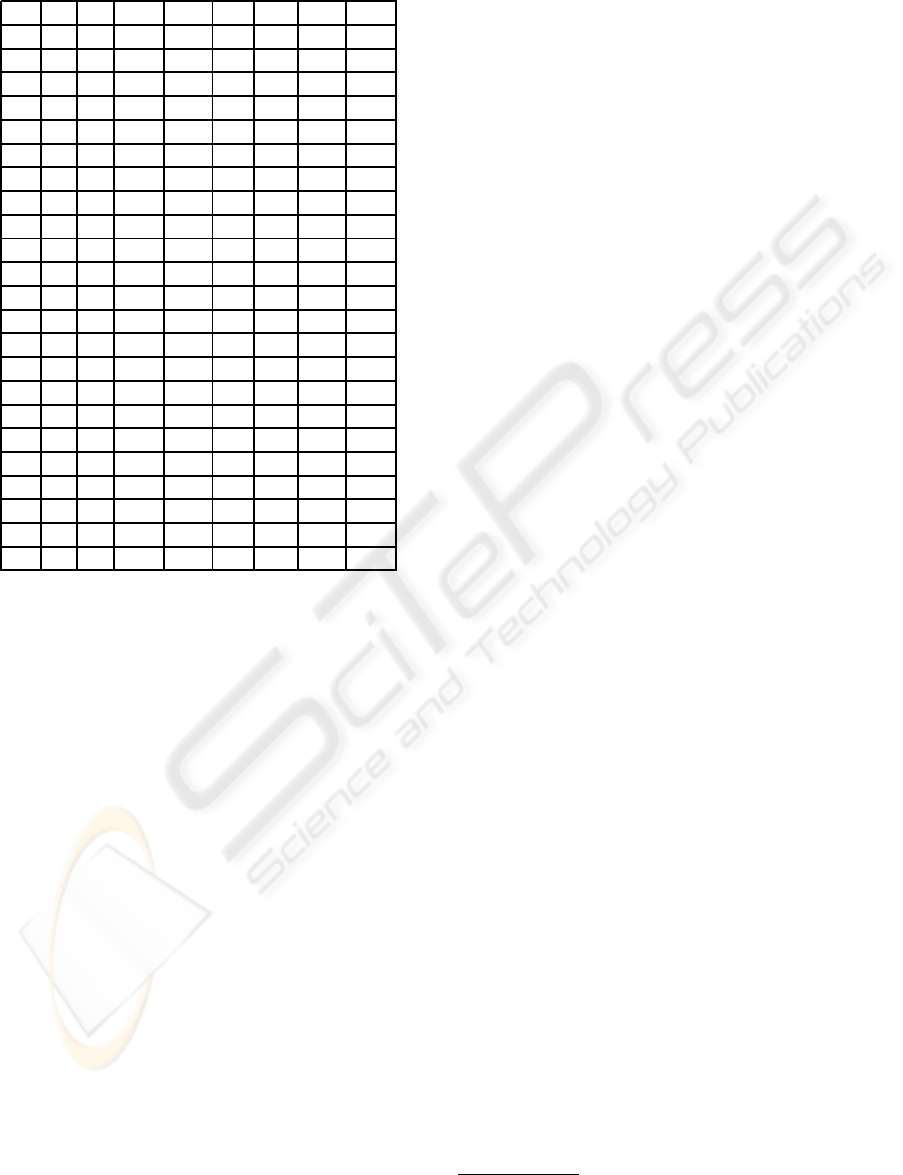
Table 1: Results of the DGA-MAS on DeArmon’s instances
vs best known results.
Pb N M LBB Best TS GA PGA DGA
1 12 22 316 316 316 316 316 316
2 12 26 339 339 339 339 339 339
3 12 22 275 275 275 275 275 275
4 11 19 287 287 287 287 287 287
5 13 26 377 377 377 377 377 377
6 12 22 298 298 298 298 298 298
7 12 22 325 325 325 325 325 325
8 27 46 344 348 352 350 355 344
9 27 51 303 311 317 303 323 305
10 12 25 275 275 275 275 275 275
11 22 45 395 395 395 395 403 395
12 13 23 448 458 458 458 462 452
13 10 28 536 544 544 540 544 540
14 7 21 100 100 100 100 100 100
15 7 21 58 58 58 58 58 58
16 8 28 127 127 127 127 129 127
17 8 28 91 91 91 91 91 91
18 9 36 164 164 164 164 164 164
19 11 11 55 55 55 55 58 55
20 11 22 121 121 121 121 123 121
21 11 33 156 156 156 156 158 157
22 11 44 200 200 200 200 203 200
23 11 55 233 233 233 235 237 233
5 DISCUSSION
We can observe that DGA-MAS obtained solutions as
good as our PGA. Furthermore, within 48% of the
solved problems, DGA-MAS outperformed our PGA
implementation of evolutionary system by a mean ad-
vantage of 0.98% in term of solution cost. DGA-MAS
is very efficient: on all instances, it is at least as good
as Carpet. On the 23 DeArmon’s instances, it out-
performs Carpet 4 times, improves 4 best known so-
lutions with one to optimality, and reaches LBB 20
times. The average deviation to LBB is roughly di-
vided by 3 compared to Carpet and becomes 0.19%.
Moreover, the mean speed up factor for the execution
times between DGA-MAS and PGA is approximately
1.7, in spite of overhead communication time spent in
DGA-MAS. Hence, the mean execution time spent to
find a solution using PGA and DGA-MAS are respec-
tively 40.3 and 24.5 seconds.
6 CONCLUSIONS
In this paper, we have proposed DGA-MAS, an effi-
cient distributed genetic algorithm which combines
the two advantages of parallelism: the computational
power and co-evolution. We implemented an infor-
mation exchange strategy based on the dynamic mi-
gration window methods that control the size and the
frequency of migration and the selective migration
model for the choice of individuals to migrate. Re-
sults confirm the positive impact of using MAS
2
strat-
egy in regard to the pure parallel GA. They also point
out that such strategies are, at a minimum, as good as
the best known methods.
In future work, we will improve the performance
of our information exchange system by the addition
of intelligent modules, thus allowing the study of the
exchange semantics of the requests for improving in-
formation. We will test also our framework on other
NP-complete problems such as planning and schedul-
ing problems.
REFERENCES
Amberg, A. and Voß, S. (2002). A hierarchical relax-
ations lower bound for the capacitated arc routing
problem. In HICSS ’02: Proceedings of the 35th An-
nual Hawaii International Conference on System Sci-
ences (HICSS’02)-Volume 3, pages 83–84, Washing-
ton, DC, USA. IEEE Computer Society.
Belenguer, J. and Benavent, E. (2003). A cutting plane al-
gorithm for the capacitated arc routing problem. Com-
put. Oper. Res., 30(5):705–728.
Beullens, P., Muyldermans, L., Cattrysse, D., and Oudheus-
den, D. (2003). A guided local search heuristic for the
capacitated arc routing problem. European Journal of
Operational Research, 127(3):629–643.
Cant`u-Paz, E. (2000). Efficient and Accurate Parallel Ge-
netic Algorithms. Kluwer Academic Publishers, Nor-
well, MA, USA.
DeArmon, J. (1981). A Comparison of Heuristics for
the Capacitated Chinese Postman Problem. Master’s
Thesis. The University of Maryland at College Park,
MD, USA.
Eldos, T. (2006). A new migration model for distributed
genetic algorithms. In The International Conference
On Scientific Computing (CSC), pages 128–134.
Goldberg, D. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA.
Golden, B., DeArmon, J., and Baker, E. (1983). Computa-
tional experiments with algorithms for a class of rout-
ing problems. Computers and Operations Research,
10(1):47–59.
Hertz, A., Laporte, G., and Mittaz, M. (2000). A tabu
search heuristic for the capacitated arc routing prob-
lem. Oper. Res., 48(1):129–135.
2
Multi-Agent System
AN EFFICIENT INFORMATION EXCHANGE STRATEGY IN A DISTRIBUTED COMPUTING SYSTEM -
Application to the CARP
345

Kim, J. (2002). Distributed genetic algorithm with mul-
tiple populations using multi-agent. In ISHPC’02:
Proceedings of the 4th International Symposium on
High Performance Computing, pages 329–334, Lon-
don, UK. Springer-Verlag.
Lacomme, P., Prins, C., and Ramdane-Ch´erif, W. (2001).
A genetic algorithm for the capacitated arc rout-
ing problem and its extensions. In Proceedings of
the EvoWorkshops on Applications of Evolutionary
Computing, pages 473–483, London, UK. Springer-
Verlag.
Luque, G., Alba, E., and Dorronsoro, B. (2005). Paral-
lel Genetic Algorithms , E. Alba (ed.), Parallel Meta-
heuristics: A New Class of Algorithms. John Wiley.
Ulusoy, G. (1985). The fleet size and mix problem for
capacitated arc routing. European Journal of Oper-
ational Research, 22(3):329–337.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
346
