THE ROLE OF SENSORY-MOTOR COORDINATION

Identifying Environmental Motion Dynamics with Dynamic Neural Networks

Stephen Paul McKibbin, Bala Amavasai, Arul N. Selvan, Fabio Caparrelli and W. A. F. W. Othman

Microsystems and Machine Vision Laboratory, Materials and Engineering Research Institute

Sheffield Hallam University Pond Street, Sheffield S1 1WB, U. K.

Keywords: Sensory-motor coordination, Particle Swarm Optimisation, Dynamic Neural Networks, Mobile robot

controllers, Bio-inspired controllers.

Abstract: We describe three recurrent neural architectures inspired by the proprioceptive system found in mammals;

Exo-sensing, Ego-sensing, and Composite. Through the use of Particle Swarm Optimisation the robot

controllers are adapted to perform the task of identifying motion dynamics within their environment. We

highlight the effect of sensory-motor coordination on the performance in the task when applied to each of

the three neural architectures.

1 INTRODUCTION

In situated agents, the actions that they perform are

the pre-cursor for the senses that they experience

which, in turn, are the basis for their next action.

Often it is assumed that senses are read and then

actions are made. It has been suggested that the

coordination of the action is as important as the

sensing and that the close coupling of these

behaviours is fundamental to building complex

behaviours (Nolfi, 2002b) and even knowledge

(O’Regan, 2001).

We investigate the task of a mobile robot being

able to identify the dynamics of a moving target in

its environment using only local information. In

nature this is an important skill that enables animals

to hunt prey, evade predators and also to

communicate with gesture or dance. The work is an

extension of the experiment by (McKibbin et al,

submitted for review) where three recurrent neural

architectures are evaluated however in this paper, a

comparison is drawn between those controllers that

are allowed to invoke Sensory-Motor Coordination

(SMC) in their motion strategy and those that are

not. The controllers have been designed in such a

way that they can be conceptually defined by a

number of features. This definition makes the study

of the effect of each feature more apparent.

The controllers that are prevented form using

SMC are given a pre-trained set of weights that

control their movement and these weights are not

adpated throughout the optimisation process. Each

controller is given the same pre-trained weights

allowing a comparison to be drawn between them

and also with the controllers that are free to adapt

their motion strategy. The work carried out in this

paper is an extension of previous work by the author

(McKibbin et al, submitted for review) and focuses

on the role of SMC in simplifying or complicating a

task that requires some amount of deliberative

processing.

2 TASK DESCRIPTION:

IDENTIFYING MOTION

DYNAMICS

The task under investigation in this paper requires a

mobile robot to discriminate and identify the two

phases of the trajectory of a moving target object

using only local information (McKibbin et al,

submitted for review).

The robot used in the task is a simulated version

of the Khepera II robot from k-team, it is cylindrical

in shape with a diameter of 32mm and it is simulated

in the Webots 3D fast prototyping software package

from Cyberbotics. The robot has two wheels

controller by independent motors (m0 and m1) that,

when spun in opposite directions, allow the robot to

rotate on the spot. It has 8 IR sensors (ds0 – ds7)

129

Paul McKibbin S., Amavasai B., N. Selvan A., Caparrelli F. and A. F. W. Othman W. (2008).

THE ROLE OF SENSORY-MOTOR COORDINATION - Identifying Environmental Motion Dynamics with Dynamic Neural Networks.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 129-136

DOI: 10.5220/0001495101290136

 SciTePress

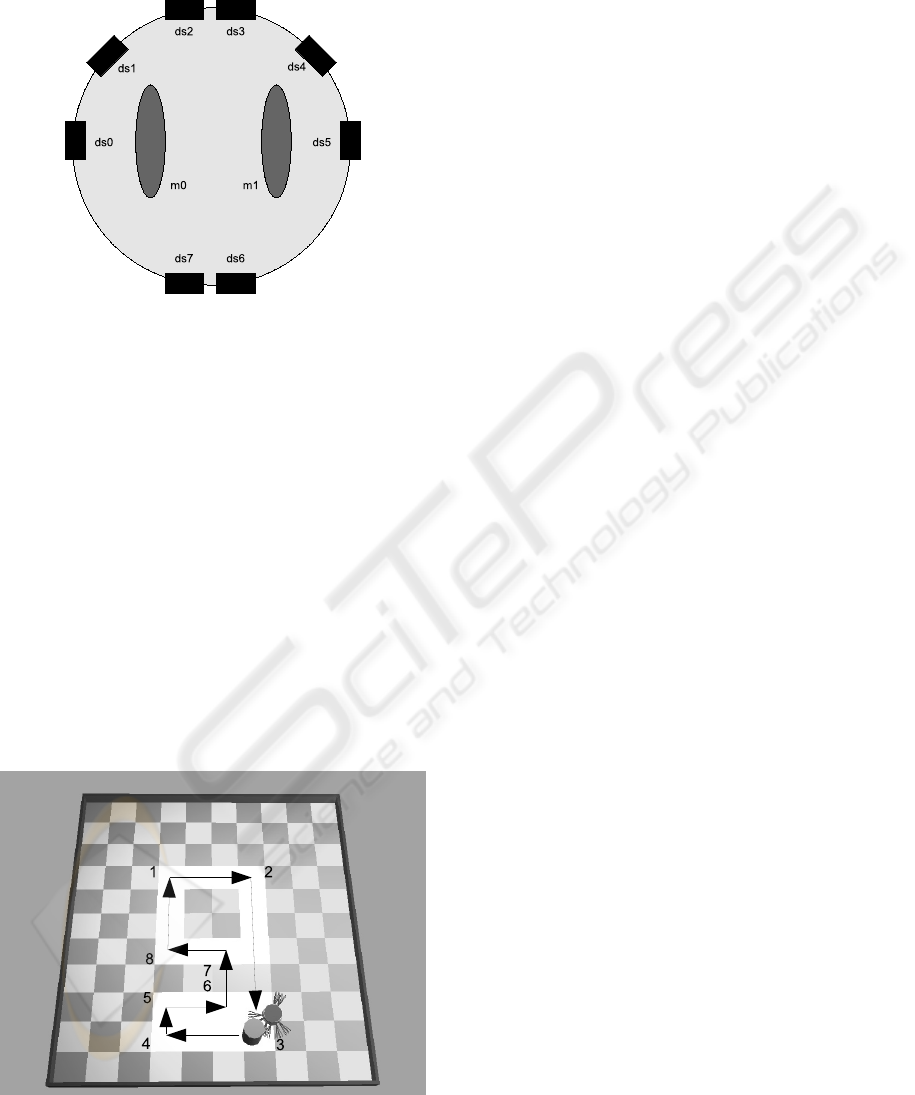
distributed around its perimeter and the particular

configuration of the sensors is shown in figure 1.

Figure 1: A functional diagram of the Khepera robot

showing the configuration of the IR sensors (ds0 – ds7)

and the motor driven wheels (m0, m1).

The target object moves in a bounded arena with

a constant “figure of 9” trajectory as shown in figure

2. It moves with a constant speed and takes no input

from the environment and will not stop if confronted

with an obstacle i.e. a robot. The size and shape of

the target are approximate to that of the robot, being

cylindrical in shape with a radius of 32mm. Since

the shape of the target is cylindrical its sensory

profile will remain the same from which ever angle

it is sensed and on its trajectory as it changes

direction and turns corners this sensory profile will

remain unchanged from the point of view of the

robot. As a result of this uniformity of shape, there is

only one distinguishing feature of the target and that

is the dynamics of its motion plan; the path of its

trajectory.

Figure 2: Screenshot of the arena showing the robot next

to the target. The arrows indicate the target’s straight

edged “figure of 9” trajectory.

The targets trajectory is considered to have two

phases, the lower part of the loop, phase0,

comprising of a flat horizontal rectangular shape,

and the upper part, phase1, comprising of a regular

square-like shape. The task for the robot is to follow

the target and to decide which phase of the trajectory

it is currently executing and to display this using an

output LED. When the LED is switched on it

denotes phase1 and when it is off it denotes phase0.

The task has 2 parts;

1) Follow the target through the “figure of 9”

loop, keeping it within sensory range

2) Indicate at each time step which phase of its

trajectory the target is currently performing

Part 1 of the task is a predicate for part 2. Since

the only sensory information available to the robot is

that provided by its IR sensors, in order to decide

which part of the loop the target is in at any given

time, the robot should be able to sense it. The only

way the robot can sense the target is when it is at

close range (<50mm). As detailed in Section 4.2, the

robot needs to remain close to the target at each time

step in order to gain fitness.

Considering part 2 of the task, the robot must be

able to discriminate the two phases of the trajectory

using only local information. As we have already

described, the sensory profile of the target remains

constant throughout each phase. The target moves in

straight lines and takes corners at 90 degrees for

each turn. The transition from one phase to another

is performed in a straight line through the grey

banded “no man’s land”. This locally uniform

motion does not give any clue to the transition

between phases. In view of these constant and

regular conditions, there are no explicit signals or

sensory states presented to the robot to aid it in its

identification task. There is no single sensory state

afforded by its environment that would allow the

robot to distinguish the two phases of the targets

movement. The robot must incorporate an ability to

add context to its current sensory information and,

depending on the context, identify the current

trajectory of the target.

3 RECURRENT NEURAL

NETWORK CONTROLLERS

The neural networks examined for this task are

DNNs with update functions that take into account

previous activation levels when producing new

activations. The architectures of the networks are

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

130

inspired by a rough model of how the human body

uses internal and external senses. The use of the

combination of external and internal senses is called

proprioception and it is this feedback system that

allows the human body to modulate its behaviour.

For example, it is through the use of proprioception

that we are able to touch our nose with our finger

whilst we have our eyes closed. Motor commands

are sent to the muscles to cause actions and so too

sensory signals are returned for processing to

provide closed loop control. The mechanisms used

to process these flows and contra-flows of

information are still active areas of research in

biology.

We describe 3 types of DNN below, each of

which have an input layer, a fully connected hidden

layer and an output layer. Each of the 3 architectures

uses different types of recurrent feedback. We have

named the 3 types of DNN Ego-sensing, Exo-

sensing and composite. They are so named due to

the type of sensing they employ;

1. The Ego-sensing controller takes the output

of the previous motor actions as inputs to

the hidden layer.

2. The Exo-sensing controller takes inputs to

the hidden layer only from the IR sensors.

3. The Composite controller uses inputs to the

hidden layer from both the motor actions

and the IR sensors.

The input layer consists of 6 input nodes each

connected to one of the 6 frontal IR sensors of the

robot. The actual input value is the IR activation

normalised in the range [0, 1]. There is also a bias

node which provides a constant input of 1. This

layer feeds forward only to the motor outputs in the

Ego-sensing architecture, in the Exo-sensing and

Composite architecture it also feeds forward to the

hidden layer and the IDU output. The hidden layer

consists of 5 nodes that are fully connected to each

other also with recursive connections that encode the

hidden node activation at the previous time step. The

input to the layer is the weighted sum of all its inputs

and each node operates with the logistic transfer

function however the output of each node is both a

function of its current inputs and its previous output

(Nolfi, 2002a). In each of the 3 types of controller

this layer feeds forward to the IDU output but does

not connect to the motor outputs. The update

equation for the hidden nodes is given in (1).

hidden_unit_out

√(mem_coef

*hidden_unit_out

) +

(1 - √(mem_coef

*hidden_unit_out

i(t-1)

)

(1)

Where hidden_unit_out

is the output of the

current hidden node in the supervisory layer and

mem_coef

is the memory coefficient associated with

the current node in the supervisory layer. The

memory coefficient for each hidden node is an

encoded parameter in the PSO algorithm and is

bound in the range [0, 1]. This parameter determines

to what extent a hidden node is affected by its

current inputs and its previous outputs. This has the

effect of altering how quickly a particular node

reacts to changes at its inputs.

3.1 Ego-Sensing Controller

The architecture for the Ego-sensing controller

consists of 2 parts. The first part is a purely reactive

system that connects the sensors at the input directly

to the motors with weighted connections. The

second part consists of a fully connected hidden

layer containing recursive feedback loops that takes

input from the sensors and feeds forward to the

Identification Unit (IDU). In an analogy with natural

systems, the first part is similar to the reflex system

found in mammals where motor actions are coupled

closely to sensory input and the second part is

loosely based on the afferent signal feedback system

in proprioception that processes self-initiated motor

actions. Figure 3 shows the reactive part on the left

with the connections directly from the sensors to the

motor shown with the thick arrow and the

deliberative part on the right with connections from

the outputs of the motors and the IDU feeding back

into the hidden layer. These connections are

weighted and they connect to each node in the

hidden layer. The hidden layer only connects to the

IDU and is thus the decision maker.

Figure 3: The architecture of the Ego-sensing controller.

The thick arrow indicates the reactive part of the network.

THE ROLE OF SENSORY-MOTOR COORDINATION - Identifying Environmental Motion Dynamics with Dynamic

Neural Networks

131

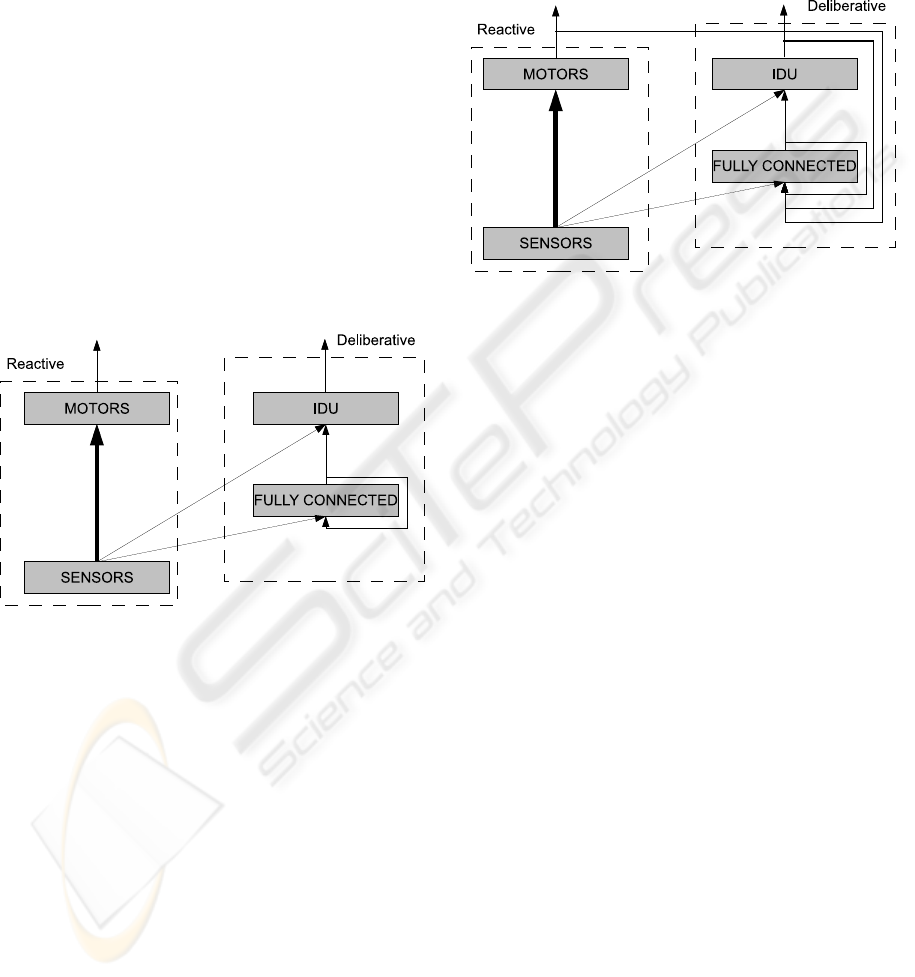
3.2 Exo-Sensing Controller

The Exo-Sensing controller also has two parts, the

reactive part with its direct coupling to the motors

and the deliberative part which processes

information over time that feeds forward to the IDU.

In the Exo-Sensing controller however, the input to

the fully connected hidden layer comes from

external information sensed by the sensor nodes.

There are no feedback connections from the output

layer thus providing no information on internal

states or actions. There is still feedback in this

controller however, provided by the recursive

connections in the hidden layer. The analogy for the

this controller is the exteroceptive sensing system

found in mammals that respond to stimuli

originating outside the body such as the sense of

touch, smell, sight and sound. Figure 4 shows the

input connections from the sensors that feed forward

to the hidden layer and to both the motor outputs and

the IDU output.

Figure 4: The architecture of the Exo-Sensing controller.

The thick arrow indicates the reactive part of the network.

3.3 Composite Controller

The Composite controller as shown in Figure 5 is a

hybrid of the Exo-Sensing and the Ego-sensing

controllers described previously. Again this

controller has two parts, the reactive part which is

the same as the other two controllers and the

deliberative part. The deliberative part in this

controller takes inputs both from the outside world

using its IR sensors and from its internal states and

actions provided by the feedback inputs from the

output layer. In fact a truer description would be that

the previous two controllers are a decomposition of

the composite controller. This represents a more

complete system as found in nature where organisms

are furnished with sensory information from the

outside world along with information of their own

internal state. An example of this would be moving

one’s hand through space, whilst watching it move

and feeling it move at the same time. The structure

of the composite controller is shown in Figure 5 with

connections to the hidden layer from both the

external sensors and from the feedback from the

output layer.

Figure 5: The architecture of the Composite controller.

The thick arrow indicates the reactive part of the network.

3.4 Pre-Trained Reactive Controller

For each of the three types or architecture detailed

above, there are 2 sets of experiments carried out. In

the first set, all of the weights for each of the

connections shown in figures 3 – 5 are allowed to

adapt freely throughout the adaptation process. In

the second set of experiments, the weights of the

connections from the sensors to the motors,

indicated by the thick arrow in each figure, are not

adapted by the PSO algorithm. The weights

associated with these connections are fixed and are

taken from a pre-trained architecture which was

trained only on its ability to follow the target. By

comparing the performance of the architectures in

each of the two experiments we should be able to

highlight the role of sensory-motor coordination in

their identification strategy. The pre-trained

architecture used is the same as the reactive part of

the network in each of the architectures, without the

hidden layer and the IDU output. Figure 6 shows the

details of the reactive network that was trained only

on its ability to follow the target. This can be

considered an expansion of the boxes labelled

“MOTORS” and “SENSORS” and the connections

between them in figures 3 – 5.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

132

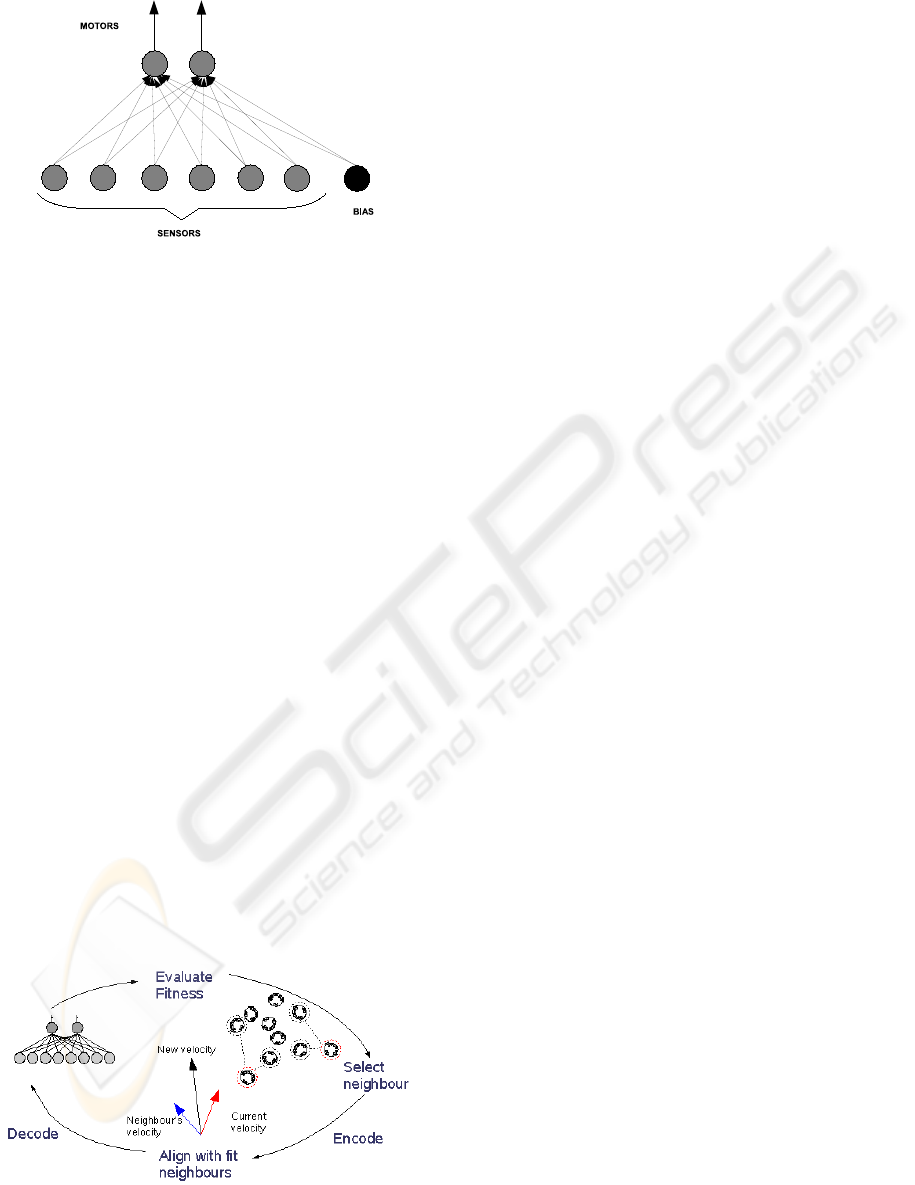
Figure 6: Reactive architecture used to obtain the pre-

trained weights for the second set of experiments.

4 PSO FOR ADAPTATION

In this paper, we employ Particle Swarm

Optimisation (PSO) to adapt the weights of a robot

neural controller. It is a bio-inspired technique that

was introduced by Kennedy and Eberhart (Kennedy,

1995) and draws inspiration from the flocking

models of birds and fish.

The free parameters, n, of an individual robot

controller are represented as the position of a single

particle that is flying through an n-dimensional

hyperspace. The particle updates its velocity at each

iteration based on its own previous best position,

pbest, and also the previous best position of its

neighbours, nbest. With time, the particles tend to

explore the solution space and, by sharing

information on the areas each of them have covered,

converge on good solutions.

The methodology for applying PSO to

adaptation in robotics is akin to that used in

Evolutionary Robotics (ER). A similar iterative

process is used for PSO in robotics, however, the

selection methods and update operators are PSO

specific. Figure 7 shows the basic methodology and

iterative process of the PSO algorithm.

Figure 7: PSO in robotics.

4.1 PSO Parameters

The PSO used in this work was the constriction

factor version that was developed by (Clerc, 1999).

= K(v

i(t-1)

+ c

- x

) + c

- x

))

K = 2/(| 2 - φ - √(φ² - 4φ)|) ,

φ = (c

+ c

φ > 4

Where:

K = constriction factor

= velocity

= position

= own best position

= group best location

= constant weight of attraction to own

best location

= constant weight of attraction to group

best location

& r

= uniform random variables in the

range [0,1]

(2)

This version of the algorithm has been shown to

always converge towards a solution (Clerc, 2002)

for a particular range of parameters. The constriction

factor version of the algorithm is given in (2).

Some standard parameter settings are used rather

than trying to tune the algorithm using empirical

methods to be problem specific (Eberhart, 2000).

The constriction factor, K, has been set to 0.729 and

the cognitive coefficient and the social coefficient

and c

) have both been set to 2.05.

The free parameters of the controller that are to

be adapted include the dynamic range of the

weights, which are randomised in the range [-10, 10]

and the memory coefficient, that has been

randomised in the range [0, 1]. These two

parameters are encoded to represent a particle’s

position vector. Each particle’s velocity vector is

also initialised to a random value in the same range

as the position vector. The velocity and position

vectors are also hard-limited to the range [-10, 10]

throughout the adaptation process. A population size

of 40 particles has been used for the swarm. This

value was achieved through empirical testing and is

an acceptable compromise between performance and

training time. The neighbourhood topology used for

each experiment is the ring topology with a

neighbourhood size of 3. Each particle has 2

neighbours and since the neighbourhood size is

restricted, the current particle can be its own

neighbourhood best particle.

THE ROLE OF SENSORY-MOTOR COORDINATION - Identifying Environmental Motion Dynamics with Dynamic

Neural Networks

133

4.2 Fitness Function

Per iteration of the algorithm, each robot is allowed

to live for 4 epochs of 2500 time steps of 96ms each.

An epoch is ended early if the robot crashes. At the

beginning of each epoch, the robot is place close to

the target in one of each of the four starting

positions; 2 in the part0

The fitness function (4) for the task has two

parts. The first part rewards for staying close to the

target object as it moves along its trajectory. The

definition of “close” here is that the robot must be

within sensory range of the target. For each time

step that the robot is close to the target

found_target_count is incremented. Fitness is given

as the percentage of the total time (4 epochs x 2500

life steps) that the robot is close to the target. If

found_target_count is greater than threshold, then

the second part of the fitness function is evaluated

and the first part is ignored.

For the pre-trained Reactive Controller, only the

first part of the fitness is evaluated since this

network has no identification output. The result is a

controller that consistently follows the target well

and attains maximum fitness in doing so.

The second part of the fitness function rewards

for the robot correctly identifying which part of its

trajectory the target is currently in. Figure 6 shows

the trajectory of the target and the robot, with its

projected IR sensor beams, next to it. The white

square shape in the upper part indicates phase1 of

the trajectory and the white rectangle shape in the

lower part indicates phase0. The grey band between

the two phases represents “no man’s land” where no

reward is given as the robot and target travel

between the two phases. The identified_

phase0_count is incremented for each time step that

the robot correctly identifies phase0 of the trajectory

and identified_phase1_count is incremented for

correctly identifying phase1. The second part of the

fitness function uses these values represented as

percentages of the correct identifications for each

phase.

fitness = (found_target_count /

max_life_span)

(4)

if(found_target_count > threshold)

fitness = 1 + (perc_identified_phase0 *

perc_identified_phase1)

where:

max_life_span

= number of epochs * life span

= 10000

threshold

= max_life_span * 0.8

= 8000

5 RESULTS

For each of the neural network architectures and

both the fixed and non-fixed weight test, the

experiment was run 10 times and the fitness data

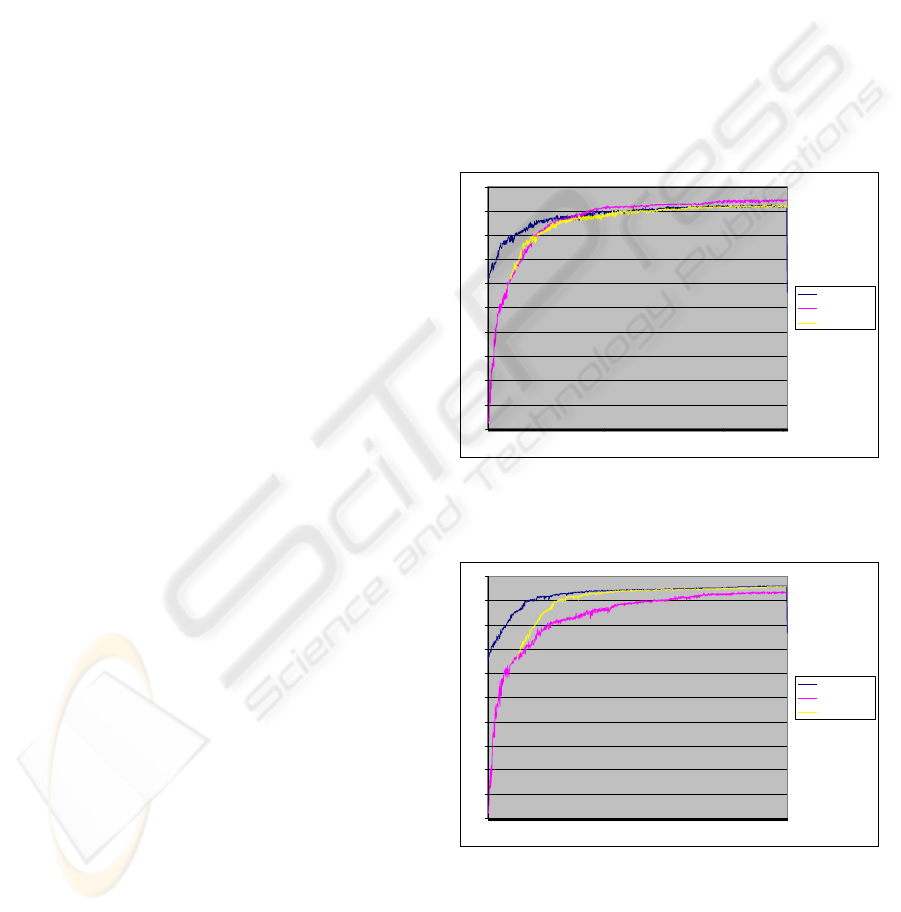
was recorded and averaged. Figures 8a, 8b and 8c

show the plots of the training data. Each plot shows

the fixed weight training data and also the same data

shifted to the right to the point where the non-fixed

weight controller achieves a similar fitness score.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

1 101 201 301 401 501 601 701 801 901

ego2_fix_avg

ego2_avg

ego2_fix_shift

Figure 8a: Training data of the best individual at each

iteration for the Ego-sensing controller. Maximum

theoretical fitness is 2.0.

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

1 101 201 301 401 501 601 701 801 901

exo3_fix_avg

exo3_avg

exo3_fix_shift

Figure 8b: Training data of the best individual at each

iteration for the Exo-sensing controller. Maximum

theoretical fitness is 2.0.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

134

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

1 101 201 301 401 501 601 701 801 901

comp2_fix_avg

comp2_avg

comp2_fix_shift

Figure 8c: Training data of the best individual at each

iteration for the Composite controller. The plots in figures

8a, 8b and 8c show the data from both the fixed weight

and non-fixed weight training. Also the fixed weight data

is shown shifted so the fitness scores start at the same

point to aid in their comparison. Data is averaged over 10

runs. Maximum theoretical fitness is 2.0.

The reason for this is to make the comparison

between the experiments more clear. The controllers

in the non-fixed weight experiment had to learn to

complete the following part of the task, part 1,

before they could gain any fitness from the

identification part, part 2. The fixed weight

controllers in each case made use of the pre-trained

reactive weights and so where already able to

complete part 1 of the task from the start of the

adaptation process.

The Ego-sensing controller was the only one of

the three architectures that performed less well when

the motion strategy of the robot was not allowed to

adapt along with the identification strategy. For the

other two architectures, when the weights

controlling robot’s motion strategy were fixed, they

were both able to train faster on the identification

task and achieve a higher maximum score.

comparison of fixed-weight averages

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

1 101 201 301 401 501 601 701 801 901

exo3_fix_avg

ego2_fix_avg

comp2_fix_avg

Figure 9: Training data of each of the three architectures

for the fixed weight version of the experiment. Data is

averaged over 10 runs. Maximum theoretical fitness is 2.0.

When comparing the three architecture types of

the fixed weight experiment, it is clear from figure 9

that the Ego-sensing controller also performs the

worst with a highest average score of 1.851. The

Exo-sensing controller and the Composite

controllers perform similarly well scoring highest

average scores of 1.921 and 1.925 respectively.

6 DISCUSSION

For the non-fixed weight experiment, each of the

controllers was able to quickly adopt a target

following behaviour. For each architecture this took

between 43 and 44 iterations. This shows that each

controller was able to learn a good motion strategy

that enabled it to remain close to the target object at

all times and that also prevented it from crashing

into the target as it suddenly changed direction when

turning corners.

In the fixed weight experiment each controller

used the same pre-trained weights from the reactive

architecture and so all of them were instantly able to

follow the target without crashing. All fitness scores

above 1.0 are attributed to the robot’s ability to

identify the phase of the target’s trajectory. Each of

the fixed weight fitness scores start above 1.0 due to

the chance level of identification ability they might

have.

When the Ego-sensing controller’s performance

in the fixed weight experiment is compared to non-

fixed weight experiment, the controller performs

better when it is allowed to adapt its own motion

strategy. The reason for this may be that the

information that is fed to the hidden layer in the

Ego-sensing controller is somewhat bland (only 2

inputs instead of 6 in the Exo-sensing version). The

Ego-sensing controller uses only its own outputs as

inputs the hidden layer and these outputs are in fact

a function of the sensor inputs. The motion strategy

used in the fixed weight experiment was not adapted

to aid in the completion of the identification task and

was used only as a method to allow the robot to

remain close to the target. This fixed motion strategy

combined with the fact the that the inputs to the

hidden layer were not as rich in patterns as some of

the other controllers may have made it harder for the

Ego-sensing controller to perform the identification

part of the task without being able to adapt its

sensory-motor coordination and thus its motion

strategy.

The Exo-sensing controller was able to perform

better in the fixed weight experiment than the

experiment where it was free to adapt its own

THE ROLE OF SENSORY-MOTOR COORDINATION - Identifying Environmental Motion Dynamics with Dynamic

Neural Networks

135

motion strategy. In the fixed weight experiment it

trained faster and reached a higher maximum

average score. Similarly the Composite controller

performed better when the weights controlling its

motion strategy were fixed. Both of these controllers

had inputs to their hidden layer from the six IR

sensors. Since this data was the raw instantaneous

sensor values, the patterns will have contained much

more information than was available to the Ego-

sensing controller. The Composite controller also

had the ego-sensing data as inputs to its hidden layer

and it scored the highest maximum average score of

the three architectures.

In previous work by the author (McKibbin et al,

submitted for review) a study of the nature of the

information being fed to the hidden layer revealed

that the fast changing sensor (exo-sensing) data can

make it more difficult for the controller to learn

slower changing temporal patterns. Conversely, the

slower changing output (ego-sensing) data seemed

to be more useful to the controller to be able to learn

the temporal patterns more quickly. However each

of the controller types was able to identify the target

trajectory with similar success after training for 1000

iterations. The main difference between the

architectures was the time taken to train. From the

experiments in this work however, it is clear that

when the motion strategy is fixed and not adaptable,

the controllers perform differently. The controllers

that had the fast changing sensor data available to

them (Exo-sensning and Composite controllers)

were more able to perform the identification task

than the controller with only the slower changing

output data (Ego-sensing controller). In the latter

case, it seems to be that the restriction of the

richness of the sensor information available to the

controller combined with it not being able to invoke

its own sensory-motor coordination strategy has

inhibited it.

It should be noted that in the fixed weight

experiment, every individual was initialised with the

weights that exhibited a pre-trained following

behaviour. This meant that every member of the

population could begin to optimise the controller for

the second part, the identification task. In the non-

fixed weight experiment only the individuals who

were able to complete the following part of the task

could gain fitness in the identification task. It should

be noted that even after 1000 iterations only 75% of

the members had learnt the following task.

7 CONCLUSIONS

This paper has presented a study of the performance

of three recurrent neural robot controllers in

identifying environmental motion dynamics.

Although all three can perform the task well, we

have shown that there are significant differences in

performance when sensory-motor coordination is

eliminated from their motion strategy. We have

highlighted the utility of DNNs as mobile robot

controllers and suggest further investigation into the

role of sensory-motor coordination in aiding

complex robot tasks.

ACKNOWLEDGEMENTS

This work has been supported by the I-SWARM project,

European FP6 Integrated Project, Project No. 507006.

REFERENCES

McKibbin, S.P., Amavasai, B., Selvan, A.N., Caparrelli,

F., Othman, W.A.F.W, 2007. Recurrent Neural Robot

Controllers: Feedback Mechanisms for identifying

Environmental Motion Dynamics. Submitted.

Clerc, M., 1999. The swarm and the queen: towards a

deterministic and adaptive particle swarm

optimization. In Proceedings of the 1999 ICEC,

Washington DC, pp1951-1957.

Clerc, M., Kennedy, J., 2002. The particle swarm -

explosion, stability, and convergence in

amultidimensional complex space. In IEEE

Transactions on Evolutionary Computation, vol. 6,

issue 1.

Eberhart, R.C. Shi, Y., 2000. Comparing inertia weights

and constriction factors in particleswarm optimization.

In Proceedings of the 2000 Congress on Evolutionary

Computation.

Kennedy, J., Eberhart, R.C., 1995. Particle Swarm

Optimisation. In Proceedings of the IEEE Int. Conf.

Neural Networks.

Nolfi, S., 2002a. Evolving robots able to self-localize in

the environment: The importance of viewing cognition

as the result of processes occurring at different time

scales. In Connection Science, vol. 14 issue 3.

Nolfi, S., Marocco D., 2002b. Active perception: A

sensorimotor account of object categorization. In

From Animals to Animats. In B. Hallam, D. Floreano,

J. Hallam, G. Hayes, J-A. Meyer (eds.) Proceedings of

the VII International Conference on Simulation of

Adaptive Behavior. Cambridge, MA: MIT Press, pp.

266-271.

O’Regan, J. K., Noe, A., 2001. A sensorimotor account of

vision and visual consciousness. In Behavioral and

Brain Sciences, 24(5):939-73.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

136