PROGRESSIVE MESH BASED ITERATIVE CLOSEST POINTS

FOR ROBOTIC BIN PICKING

Kay Boehnke and Marius Otesteanu

Communication Department, Polytehnica University Timisoara, Bd. Vasile Parvan, nr. 2, 300223 Timisoara, Romania

Keywords: Iterative Closest Points, Surface registration, Progressive Mesh, laser range sensors, Object localization,

Robotic bin picking.

Abstract: This paper describes a hierarchical registration process using the iterative closest point algorithm combined

with a Progressive Mesh. To find the exact pose of objects in a robotic bin picking process we simulate the

appearance of object poses and compare them with the real range data provided by laser range sensors. The

coarse pose is estimated in a first step and then refined with the well known iterative Closest Point (ICP)

algorithm combined with Progressive Meshes for hierarchical object localization. We evaluate our approach

with different test scenarios and show the comprehensive potential of this idea for other registration

problems.

1 INTRODUCTION

Today robots get more and more involved in

industrial processes, because they are superior to

man regarding requirements on strength, speed and

endurance. Robotic automation processes became

very successful in the last years, and offers a wide

range for research. The task of robotic bin picking is

easy to explain: Pick a known or unknown object out

of a bin with an unsupervised industrial robot. This

is called the “bin picking problem”(Hashimoto &

Sumi,1999), (Katsoulas, 2005). It is also known as

the de-palletizing problem, which occurs in nearly

every industrial sector. The approach in this paper

focuses on the object localization step, which is the

most challenging step in the whole process. We

introduce a simulation of a full laser scanning

process. Industrial laser range sensors are modelled

to transfer a cad-aided-design (CAD) model to a

2.5D range data representation. This virtual range

data is aligned to the real range data of the scene

with the help of combination of the Iterative Closest

Point algorithm (Besl & McKay, 1992) and

Progressive Meshes (Hoppe, 1996). Beside the

significant improvement in speed our approach leads

to better accuracy and robustness of the whole

system. After the overview in section 2 the coarse

pose estimation for a pose pre-selection is

introduced in section 3. In the refinement step of our

system we use the Progressive Mesh based Iterative

Closest Point (PMICP) algorithm to derive optimal

solution with high accuracy. We evaluate our

approach with test range data in section 4 and

conclude with upcoming extensions of our approach.

2 SYSTEM OVERVIEW

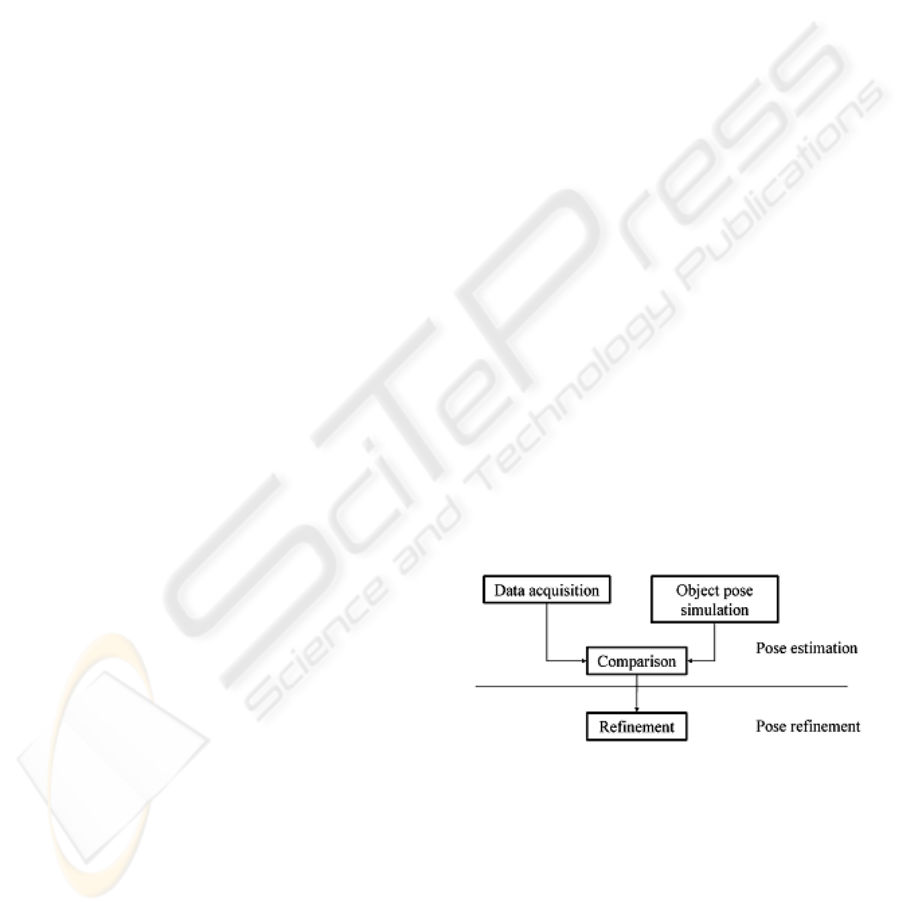
An overview of the proposed object localization

system is shown in the figure 1.

Figure 1: System overview.

The object localization is separated into pose

estimation and refinement. To reduce the number of

possible poses in the computational expensive

refinement step, we make a pre-selection in the pose

estimation step. The refinement step uses a modified

registration algorithm to increase the accuracy. The

components of our system are introduced in detail in

the following sections.

121

Boehnke K. and Otesteanu M. (2008).

PROGRESSIVE MESH BASED ITERATIVE CLOSEST POINTS FOR ROBOTIC BIN PICKING.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 121-124

DOI: 10.5220/0001494801210124

 SciTePress

3 POSE ESTIMATION

The purpose of the object pose estimation is to find

adequate coarse positions of an object in the scene.

The object pose simulation creates a virtual

range image (VRI) with help of a simulated sensor

and a virtual scene points. The triangulated CAD-

based object model is used to generate virtual range

images with the help of the simulated range sensor.

The sensor model virtually scans the object and

produces a range image in the same way like the real

scene. For every possible position and orientation a

VRI is produced. This VRI is indexed with a known

position and orientation of the model in a database.

The range data representation of the VRI and the

real range image (RRI) are datasets of three

dimensional points with the position x, y and z.

Every VRI is compared to the RRI determining the

difference between the distance values z for acquired

data from the range sensor and the simulated data

with the following error function:

∑∑

−=

RRIVRI

jizjiz

Error

),(),(

(1)

The error is defined as the mean of the difference

between every distance value Z

of the simulated

object and the distance value Z

of the scene. We use

this efficient calculation considering the fact, that

both coordinate systems of RRI and VRI are equal

due to knowledge of the real scene setup. Different

VRI’s for different kind of objects are compared to

the RRI in the same way. So the object classification

is integrated in the step of object localization. One

advantage of this pre-selection of matching positions

is the fact, that all VRI can be calculated offline and

stored in a database. So the process for our coarse

pose estimation can be summarized in that way:

 the RRI is delivered by the sensor

 all VRI in the database (one for each

possible pose) are compared to the RRI

 these VRI with the best error value are

selected for pose refinement

We take the VRI candidates within the best 10-

20% of all error values in the coarse pose estimation.

These VRI candidates are delivered to the pose

refinement process, starting with the best matching

candidate.

4 POSE REFINEMENT

In the previous section the coarse pose estimation

creates an error value for every pose. The best VRI

candidates were chosen and used as input for the

pose refinement to find the best matching candidate.

The task of the pose refinement is to find a nearly

exact match between the object in the scene and the

simulated image. The classical and most commonly

used algorithm for determining rigid transformations

is the Iterative Closest Point algorithm (Besl &

McKay, 1992), (Chen & Medioni, 1992). Because of

the slow convergence speed, the ICP was improved

by many researchers (Rusinkiewicz & Levoy, 2001).

We use the ICP algorithm in combination with

Progressive Meshes (Hoppe, 1996) to find the exact

matching pose for every VRI candidate in the real

scene captured by the laser range sensor. We call

this combination Progressive Mesh Iterative Closest

Point Algorithm (PMICP). The major problems of

the ICP algorithm are the low performance

calculating a huge amount of points in scene and

model and its sensitivity to outliers (Rusinkiewicz

and Levoy, 2001). In every iteration step all points

of the two datasets must be compared to each other

with a complexity of O(N

RRI

VRI

) where N

RRI

and

VRI

are the numbers points in the datasets. Our

hierarchical approach now reduces this complexity

by comparing only a reduced number of points N

each dataset. The representation of Progressive

Meshes provides a highly efficient implementation

for adjusting the level of detail in a point dataset and

includes an inbuilt noise reduction. This

representation is given by a set of meshes M

to M

is the mesh with the lowest accuracy and M

the mesh with the highest accuracy. The process of

generating Progressive Meshes from point datasets

is described in detail in the work of Hoppe et.

al.(1993). In our experiments we choose the simplest

way to connect the hierarchy of the Progressive

Mesh representation to the ICP: The Progressive

Mesh representation M

is increased by a fixed

increment and starts with a defined level of detail in

each iteration step. The obvious advantage is the

increased performance. But the profoundly effect is

the increased robustness against outliers. By

reducing the mesh up to M

outliers can no longer

affect the result of the distance calculation. The

shape of the model in representation of M

is similar

to the M

representation of the scene representation.

This leads to a very good initial position in the

iterative process of the closest point algorithm. We

have evaluated our PMICP with several experiments

which are described in the next section.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

122

5 EXPERIMENTAL RESULTS

It is obvious that some results depend on the used

registration data and the initial pose. In our

applications the ICP has to find the transformation

between range images (RRI) and the simulated range

images (VRI), which are more or less similar in

shape to the “fractal” scenario of the following test

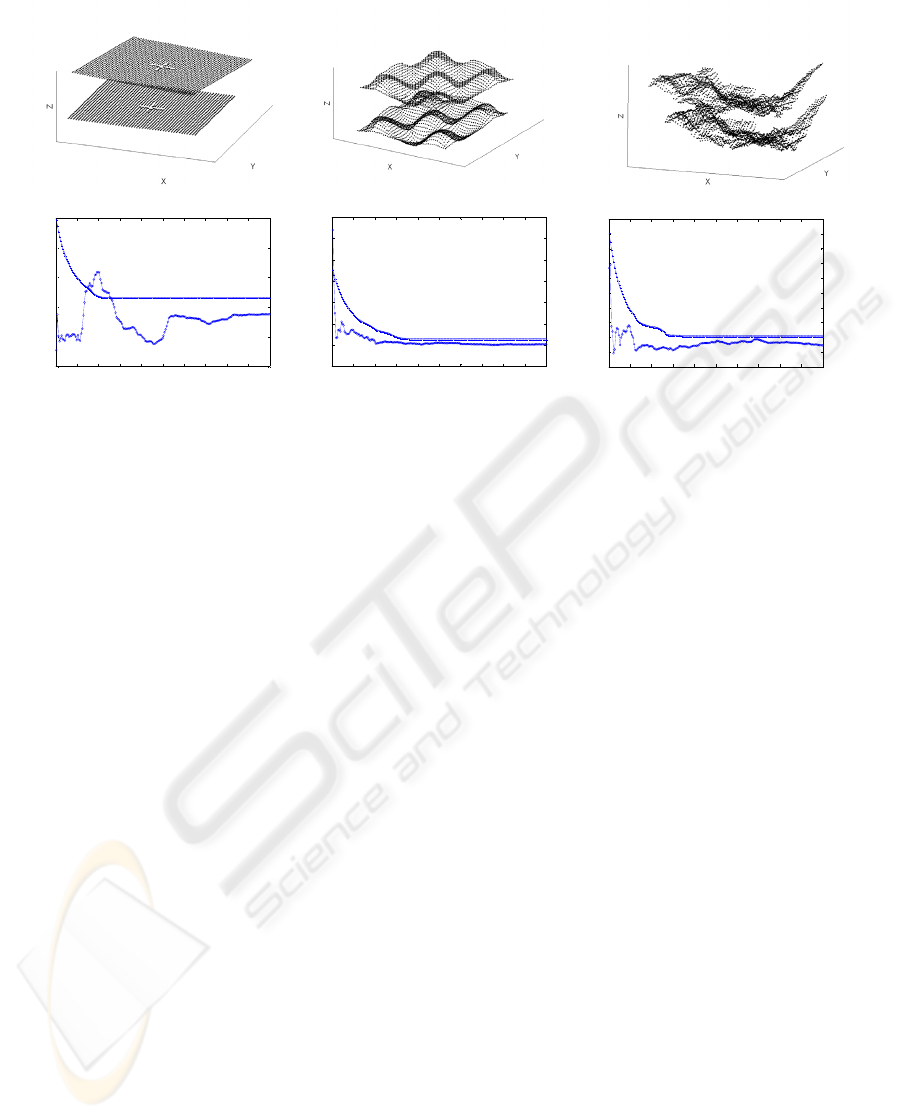
scenarios. To evaluate our idea we used the

reference datasets of Rusinkiewicz and Levoy

(2001). We us the same test environment with

synthetic meshs of 2000 points added with Gaussian

noise and outliers. The datasets are shown in figure

2a. The “incised” dataset has two lines in shape of

an “X” in the middle of a planar surface. This

“wave” dataset is an easy scenario because of low

frequency features and a smooth surface. In opposite

to the wave scenario the “fractal” dataset represents

landscape data of terrain registration and has

features in all level of details.

5.1 Results

To compare our results we implemented the standard

ICP algorithm according to (Besl & McKay, 1992)

without approximation and any other possible

improvements described by Rusinkiewicz and Levoy

(2001). We changed the distance error calculation

from Euclidian distance to

()( )()

zzyyxxE −+−+−=

∑

(2)

to avoid computational floating point errors and

increase calculation performance. We implemented

the Progressive Mesh based Iterative Closest Point

Algorithm (PMICP) based on the Progressive Mesh

implementation of Hoppe in DirectX (Hoppe 1998).

In our tests we start with an initial meshs consisting

of five triangles and increase the number of vertices

in the meshs by five triangles for each iteration step.

The initial M

does not suffer from outliers like

the standard ICP does. With the increasing iteration

steps and the number of points in the datasets the

PMICP implementation degenerates more and more

to the reference algorithm with a better robustness.

The convergence performance (figure 2b) of the

“wave” scenario is similar to the “fractal” scenario.

The algorithm outperforms the standard algorithm in

the “incised” scenario over most iteration steps. The

higher error between iteration step 20 and 40 shows

the rotation ambiguity of the alignment of two plane

surfaces. Especially in the first few iteration steps

the PMICP aligns the datasets to a good initial pose.

The squared distance error is always smaller when

comparing to the standard ICP.

All this experiments concentrate on convergence

robustness and final distance error issues. But the

experiments show, beside the improvements

mentioned above, that the overall performance of the

refinement process can be increased significantly.

The complexity of the ICP algorithm depends

mainly on the number of points in the dataset. The

search of the closest points has a computational

complexity of

O(N

). We reduce the number of

2 a) “incised” “wave” “fractal”

2 b)

0 20 40 60 80 100 120 140 160 180 200

3.5

4.5

5.5

x 10

iterations

squared error distance

0 20 40 60 80 100 120 140 160 180 200

3.5

4.5

5.5

6.5

x 10

iterations

squared distance error

0 20 40 60 80 100 120 140 160 180 200

3.2

3.4

3.6

3.8

4.2

4.4

4.6

4.8

x 10

iterations

squared distance error

Figure 2: Test scenarios (2a) with convergence performance (2b).

PROGRESSIVE MESH BASED ITERATIVE CLOSEST POINTS FOR ROBOTIC BIN PICKING

123

points in the dataset, starting with only a few points

and increase the number in every iteration step. The

computational complexity is reduced in average to

O((0.5*N

)*(0.5*N

)) assuming we do not stop the

iteration until we reach the end (M

mesh).

If the iteration process is stopped, because the

ICP reached the minimum, the performance of our

implementation is always better than

O((0.5*N

)*(0.5*N

)). Our Progressive Mesh ICP

experiments need in average 25% of the time of the

standard ICP implementation.

6 FURTHER EXTENSIONS

Many of known modifications of the ICP can be

combined with the PMICP without loss of

generalization. For example the performance in the

closest points search is often increased using Kd-

Trees implementations (Z. Zhang, 1994) to

O(N

*log(N

)). The Kd-Tree search could be used in

addition to our PMICP leading to a significant

improvement in speed especially in the higher level

of details. The ICP algorithm is known to be very

sensitive to wrong initial poses of the two datasets

because of the fact, that the ICP will always

converge to the local minimum (which is of course

commonly not identical to the global minimum). So

the determination of the optimal initial start value

for the number of points in the mesh is very

important. In the current implementation the level of

detail in the Progressive Mesh is connected to

number of iterations in the ICP. Finding the optimal

number of points for each iteration step in ICP

iterations is one of possible improvements in the

next steps of our research.

7 CONCLUSIONS

We described a system to align range data surfaces

in a context of industrial process automation. We

focused on the improvements in the refinement step

of our hierarchical object localization system. The

well known and proven ICP Algorithm is modified

with the use of Progressive Meshes. To be sure to

meet the requirements of different applications we

evaluated our system with test scenarios, which

cover many types of possible range data scenes.

The simulation of real scenes offers the

possibility to use our approach in many scenarios.

The described two-step object localization is

integrated in our system robotic bin picking covering

different application scenarios (Boehnke, 2007).

ACKNOWLEDGEMENTS

The author would like to thank S. Rusinkiewicz for

providing the datasets. This work was supported in

part by VMT (Pepperl+Fuchs Group) in Mannheim/

Germany. The author wants to thank P. Roebrock,

M. Kleinkes, W. Neddermeyer, W. Winkler, and K.

Lehmann for their support in this project.

REFERENCES

Besl, J.P., N.D. McKay, 1992. A Method for Registration

of 3-D Shapes, In IEEE Trans. on Pattern Analysis

and Machine Intelligence, vol 14, pp. 239-256

Boehnke, K., 2007. Object localization in range data for

robotic bin picking, In IEEE Proceedings on

Automation Science and Engineering, pp. 572-577

Chen, Y., Medioni, G., 1992. Object Modelling by

Registration of Multiple Range Images, In Image and

Vision Computing, vol. 10, pp. 145-155

Hashimoto, M., Sumi, K., 1999. 3d object recognition

based on integration of range image and grey-scale

image, In Proc. British Machine Vision Conference

pp. 253–262

Hoppe, H., 1996. Progressive Meshes, In Computer

Graphics (SIGGRAPH ’96 Proceedings), pp. 99–108.

Hoppe, H., DeRose, T., Duchamp, T., McDonald, J.,

Stuetzle, W., 1993. Mesh optimization. In Computer

Graphics (SIGGRAPH '93 Proceedings) pp 19-26

Hoppe, H., 1998. Efficient Implementation of Progressive

Meshes, In Comp.. & Graphics Vol.22/1, pp. 27-36

Katsoulas, D., 2004. Robust recovery of piled box-like

objects in range images, Ph.D. dissertation, Dept.

Computer Science, Freiburg Univ., Germany

Rusinkiewicz, S., Levoy, M., 2001. Efficient variants of

the ICP algorithm, In Proc. of the Third Intl. Conf. on

3D Digital Imaging and Modeling, pp. 145–152

Zhang, Z.,1994. Iterative point matching for registration of

free-form curves and surfaces. In the International

Journal of Computer Vision, 13(1):119–152.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

124