
FOOTSTEP PLANNING FOR BIPED ROBOT BASED ON FUZZY
Q-LEARNING APPROACH
Christophe Sabourin, Kurosh Madani
Laboratoire Images, Signaux, et Syst`emes Intelligents (LISSI EA / 3956), Universit´e Paris-XII
IUT de S´enart, Avenue Pierre Point, 77127 Lieusaint, France
Weiwei Yu, Jie Yan
Flight Control and Simulation Institute, Northwestern Polytechnical University, Xi’an 710072, China
Keywords:
Biped robots, Footstep planning, Fuzzy Q-Learning.
Abstract:
The biped robots have more flexible mechanical systems and they can move in more complex environment
than wheeled robots. Their abilities to step over both static and dynamic obstacles allow to the biped robots to
cross an uneven terrain where ordinary wheeled robots can fail. In this paper we present a footstep planning
for biped robots allowing them to step over dynamic obstacles. Our footstep planning strategy is based on a
fuzzy Q-learning concept. In comparison with other previous works, one of the most appealing interest of our
approach is its good robustness because the proposed footstep planning is operational for both constant and
random velocity of the obstacle.
1 INTRODUCTION
In contrast with the wheeled robots, the biped robots
have more flexible mechanical system and thus they
can move in more complex environment. Actually,
their abilities to step over both static and dynamic
obstacles allow to the biped robots to cross an un-
even terrain where regular wheeled robots can fail.
Although there are a large number of papers dealing
with the field of biped and humanoid robots (see for
examples (Hackel, 2007) and (Carlos, 2007)), only a
few of publication researches concern the path plan-
ning for biped robots (Ayza, 2007), (Chestnutt, 2004),
(Sabe, 2004). In fact, the design of a path planning for
biped robots into indoor and outdoor environment is
more difficult than for wheeled robots because it must
take into account their abilities to step over obstacles.
Consequently, path planning with obstacle avoidance
strategy like the wheeled robots is not sufficient.
Generally, the previous proposed approaches in
the field of path planning for biped robots arebased on
a tree search algorithm. In (Kuffner, 2001) , Kuffner
et al. have proposed a footstep planning approach us-
ing a search tree from a discrete set of feasible foot-
step locations. This approach has been validated on
the robot H6 (Kuffner, 2001) and H7 (Kuffner, 2003).
Later, this strategy has been extended for the robot
Honda ASIMO (Chestnutt, 2005). Although the foot-
step planning proposed by Kuffner seems an interest-
ing way to solve the problem of the path planning
for biped robots, the main drawbacks are on the one
hand the limitation at 15 foot placements (Kuffner,
2001) in order to limit the computational time, and
on the other hand, this approach is operational only
in the case of the predictable dynamic environments
(Chestnutt, 2005). In this paper, we present a new
concept of a footstep planning for biped robots in
dynamic environments. Our approach is based on a
Fuzzy Q-learning (FQL) algorithm. The FQL, pro-
posed by Glorennec et al. (Glorennec, 1997) (Jouffe,
1998), is an extension of the traditional Q-learning
concept (Watkins, 1992) (Sutton, 1998) (Glorennec,
2000) allowing to handle the continuous nature of the
state-action. In this case, both actions and Q-function
may be represented by Takagi-Sugeno Fuzzy Infer-
ence System (TS-FIS). After a training phase, our
footstep planning strategy is able to adapt the step
length of the biped robot only using a Fuzzy Inference
System. However, our study is limited to the sagittal
plane and does not take into account the feasibility of
the joint trajectories of the leg. In fact, the footstep
planning gives only the position of the landing point.
But the first investigations show a real interest of this
approach because:
183
Sabourin C., Madani K., Yu W. and Yan J. (2008).
FOOTSTEP PLANNING FOR BIPED ROBOT BASED ON FUZZY Q-LEARNING APPROACH.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - RA, pages 183-188
DOI: 10.5220/0001486701830188
Copyright
c
SciTePress

• The computing time is very short. After the learn-
ing phase, the footstep planning is based only on
a FIS,
• The footstep planning is operational for both pre-
dictable and unpredictable dynamic environment
allowing to increase the robustness.
This paper is organized as follows. In Section 2,
the Fuzzy Q-learning concept is presented. Section
3 describes the footstep planning based on the Fuzzy
Q-learning. In section 4, the main results, obtained
from simulations, are given. Conclusions and further
developments are finally set out in section 5.
2 FUZZY Q-LEARNING
CONCEPT
Reinforcement learning (Sutton, 1998) (Glorennec,
2000) involves problems in which an agent interacts
with its environment and estimates consequences of
its actions on the base of a scalar signal in terms of
reward or punishment. The goal of the reinforcement
learning algorithm is to find the action which maxi-
mize a reinforcement signal. The reinforcement sig-
nal provides an indication of the interest of last chosen
actions. Q-Learning, proposed by Watkins (Watkins,
1992), is a very interesting way to use reinforcement
learning strategy. However, the Q-Learning algorithm
developed by Watkins deals with discrete cases and
assumes that the whole state space can be enumerated
and stored in a memory. Because the Q-matrix values
are stored in a look-up table, the use of this method
becomes impossible when the state-action spaces are
continuous. For a continuous state space, Glorenec
et al. (Glorennec, 1997) (Jouffe, 1998) proposed to
use fuzzy logic where both actions and Q-function
may be represented by Takagi-Sugeno Fuzzy Infer-
ence System (TS-FIS). Unlike the TS-FIS in which
there is only one conclusion for each rule, the Fuzzy
Q-Learning (FQL) approach admits several actions
per rule. Therefore, the learning agent has to find the
best issue for each rule.
The FQL algorithm uses a set of N
K
fuzzy rules
such as:
IF x
1
is M
1
1
AND x
i
is M
j
i
THEN
y
k
= a
1
k
with q = q
1
k
or y
k
= a
l
k
with q = q
l
k
or y
k
= a
N
l
k
with q = q
N
l
k
(1)
x
i
(i = 1..N
i
) are the inputs of the FIS which represent
the state space, N
i
is the size of the input space. Each
fuzzy set j for the input i is modeled by a membership
function M
j
i
and its membership value µ
j
i
. a
l
k
and q
l
k
are respectively the l
th
possible action for the rule k
and its corresponding Q-value (k = 1..N
k
;l = 1..N
l
).
At each step time t, the agent observes the present
state X(t). For each rule k, the learning system has
to choose one action among the total N
l
actions us-
ing an Exploration/Exploitation Policy (EEP). In our
approach, ε-greedy algorithm is used to select the lo-
cal action for each activated rule. The action with the
best evaluation value (max(q
l
k
),l = 1..N
l
) has a prob-
ability P
ε
to be chosen, otherwise, an action is chosen
randomly among all possible actions. After, the ex-
ecution of the next computed action, the agent may
update the Q-value using of a reinforcement signal.
The algorithm of the FQL may be decomposed into
four stages:
• After the fuzzification of the perceived state X(t),
the rule values α
k
(t) are computing using equa-
tion (2):
α
k
(t) = µ
j
1
µ
j
2
................µ
j
Ni
(2)
• The final actionY(t) is computed through two lev-
els of computation: in the first level, local action l
in each activated rule is determined by using EEP,
and in the second level global action is calculated
as a combination of all local actions. Equations
(3) and (4) give respectively the computation of
the global action Y(t) and the corresponding Q(t)
value according to the truth value α
k
(t):
Y(t) =
N
k
∑
k=1
α
k
(t)a
l
k
(t) (3)
Q(t) =
N
k
∑
k=1
α
k
(t)q
l
k
(t) (4)
• Matching up the new action, given by Y(t)
and taking into account the environment’s reply,
Q(t)may be updated using equation (5):
∆Q(t) = β[r + γV
max
(t + 1) − Q(t)] (5)
Where V
max
(t + 1) is the maximum Q-value for
the activated rule at the next step time t + 1:
V
max
(t + 1) =
N
k
∑
k=1
α
k
(t + 1)max(Q
l
k
(t + 1)) (6)
γ is a discount factor which can be chosen from 0
to 1. If it is close to 0, the reinforcement informa-
tion tends to consider only the immediate reward,
while if it is closer to 1, it considers the future
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
184
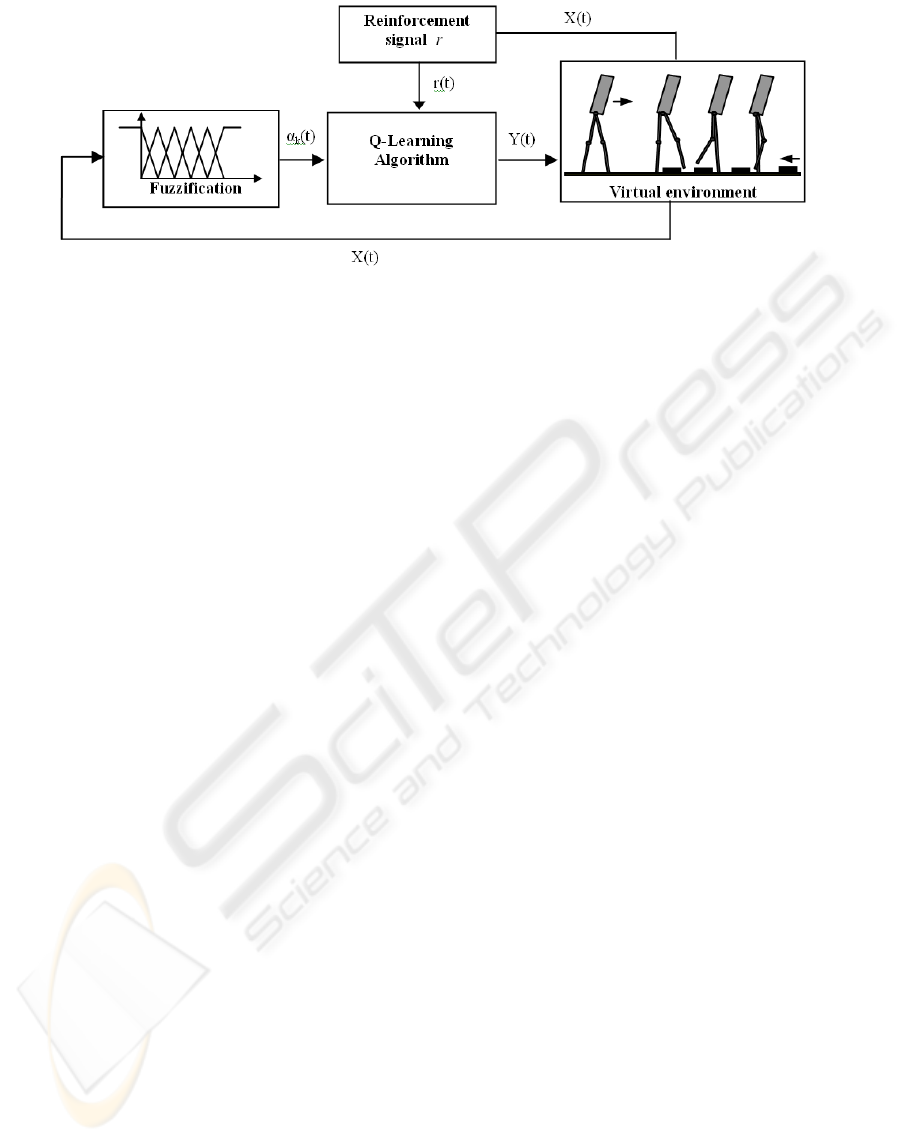
Figure 1: Footstep planning strategy.
rewards with greater weight. β is a learning rate
parameter allowing to weight the part of the old
and new rewards in a reinforcement signal r.
• Finally, for each activated rules, the correspond-
ing elementary quality ∆q
l
k
of the Q-matrix is up-
dated as:
∆q
l
k
= Q(t)α
k
(t) (7)
3 FOOTSTEP PLANNING
The proposed footstep planning is based on a FQL ap-
proach. Our aim is to design a control strategy allow-
ing to adjust automatically the step length of a biped
in order that the robot avoids dynamic obstacles by
using step over strategy. As figure 1 shows it, our
footstep planning may be divided into four parts:
• The first part involves a fuzzification of inputs of
the state X(t),
• The second concerns the FQL algorithm allowing
to compute the length of the step,
• The third part allows simulating dynamic environ-
ment into which the robot moves,
• And the fourth part gives the reinforcement signal.
3.1 Virtual Dynamic Environment
The both robot and obstacle move in sagittal plane but
in opposite directions. We consider that the walking
of the biped robot may include as well strings of sin-
gle support phases (only one leg is in contact with the
ground) as instantaneous double support phases (the
two legs are in contact with the ground). The biped
robot may adjust the length of its step but we con-
sider that the duration of each step is always equal
to 1s. The size and velocity of the obstacle are in-
cluded into [0,0.4m] and [0,0.4m/s] ranges respec-
tively. Although the robot has the ability to adjust
its step length, there are two possibilities in which the
robot may crash with the obstacle. First one occurs
when the length of the step is not correctly adapted
according to the position of the dynamic obstacle. In
this case, the swing leg touches directly the obstacle
during a double support phase. The other case cor-
responds to the situation where the obstacle collides
with the stance leg during the single or double sup-
port phase.
3.2 Fuzzification
The design of our footstep planning is based on both
Takagi-Sugeno FIS and Q-learning strategies. Conse-
quently, it is necessary to use a fuzzification for each
input. In the proposed approach, we use two inputs
in order to perform a correct footstep planning. These
inputs are the distance between the robot and the ob-
stacle d
obs
and the velocity of the obstacle v
obs
. d
obs
and v
obs
are updated at each double support phase.
d
obs
correspondsto the distance between the front foot
and the first side of the obstacle. v
obs
is computed
from the distance covered during 1s. The fuzzification
of v
obs
and d
obs
is carried out by using respectively 6
and 11 triangular membership functions. Figure 2(a)
and 2(b) gives the membership functions of the obsta-
cle velocity and distance respectively.
3.3 FQL-based Step Length
The FQL algorithm uses a set of fuzzy rules such as
equation (1). For the proposed problem, the number
of the rules is 66 (6 and 11 membership functions
for velocity and distance of the obstacle respectively).
For each rules, we define 5 possible outputs which
are [0.1,0.2,0.3, 0.4,0.5]m. In fact, these outputs cor-
FOOTSTEP PLANNING FOR BIPED ROBOT BASED ON FUZZY Q-LEARNING APPROACH
185

(a) Obstacle velocity v
obs
(in m/s).
(b) Obstacle distance d
obs
(in m).
Figure 2: Membership functions used for the input space.
respond to the length of the step. Consequently, at
each step time, the Fuzzy Q-Learning algorithm needs
to choose one output among five possible outputs for
each activated rules. It must be pointed out that the
chosen output is included into a discrete set, but the
real output Y(t) is a real number dues a fuzzification.
During the simulation, the size of the obstacle is con-
stant but the velocity of the obstacle may be modi-
fied. At each episode, initialization of some param-
eters are necessary. The initial distance between the
biped robot and the obstacle is always equal to 2.5m.
The velocity of the obstacle is chosen randomly into
the interval [0,0.4]m/s. During one episode, the step
length of the robot is computed using the FQL algo-
rithm described in section 2. Consequently, the biped
robot moves step by step towards the obstacle dur-
ing the episode. The episode is finished whether the
robot steps over the obstacle (success) or if the robot
crashes into obstacle (failure). The discount factor
γ and the learning rate parameter β are equal to 0.8
and 0.1 respectively. This parameters have been cho-
sen empirically after several trials in order to assure a
good convergence of FQL algorithm. The probability
P
ε
is equal to 0.1 and means that the random explo-
ration is privileged during the learning phase.
3.4 Reinforcement Signal
The reinforcement signal provides an information in
terms of reward or punishment. Consequently, the re-
inforcement signal informs the learning agent about
the quality of the chosen action. In our case, the learn-
ing agent must find a succession of action allowing
to the biped robot to step over an obstacle. But here
the obstacle is a dynamic object which moves towards
the biped robot. Consequently, the reinforcement in-
formation have to take into account of the velocity
of the moving obstacle. In addition, the position of
the foot just before the stepping-over is very impor-
tant as well. On the base of these considerations, we
designed reinforcement signal in two parts.
Firstly, if x
rob
< x
obs
where x
rob
and x
obs
give the
positions of the robot and of the obstacle respectively:
• r = 0, if the robot is still far from obstacle,
• r = 1, if the position of the robot is appropriate to
cross the obstacle at next step,
• r = −1, if the robot is too close to the obstacle.
In this first case, r is computed with the following
equation:
r =
0 if ( x
rob
≤ (x
obs
− 1.2v
obs
∆t) )
1 if (x
rob
> (x
obs
− 1.2v
obs
∆t))
AND (x
rob
≤ (x
obs
− 1.1v
obs
∆t)).
-1 if (x
rob
> (x
obs
− 1.1v
obs
∆t))
(8)
x
rob
and x
obs
are updated after each action. v
obs
∆t rep-
resents the distance covering by obstacle during the
time ∆t. As the duration of the step is always equal
1s, ∆t is always equal to 1s.
Secondly, if (x
rob
≥ x
obs
):
• r = −2, if the robot crashes into the obstacle at the
next step,
• r = 2, if the robot crosses the obstacle at the next
step.
In this last case, r is given by equation (9).
r =
-2 if ( x
rob
≤ (x
obs
+ L
obs
) )
2 if ( x
rob
> (x
obs
+ L
obs
) )
(9)
Where L
obs
is the size of the obstacle.
4 SIMULATION RESULTS
In this section, we present the main results related the
footstep planning based on FQL approach by using
MATLAB software. It must be noticed that our goal
is to design a control strategy allowing to give a path
planning into a dynamic environment for biped robot
but we do not take into account the dynamic of the
biped robot. We consider only discrete information
allowing to compute the landing position of the foot.
In addition, we consider only flat obstacles in the fol-
lowing simulations.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
186
4.1 Training Phase
During the training phase, the goal of the learning
agent is to find the best rules in order that the biped
robot crosses the obstacle. On the base of the previous
description, we trained the Q-matrix during 10000
episodes. After a full training, we test the footstep
planning approach with 1000 velocity samples cover-
ing uniformly the input range [0,0.4]m/s.
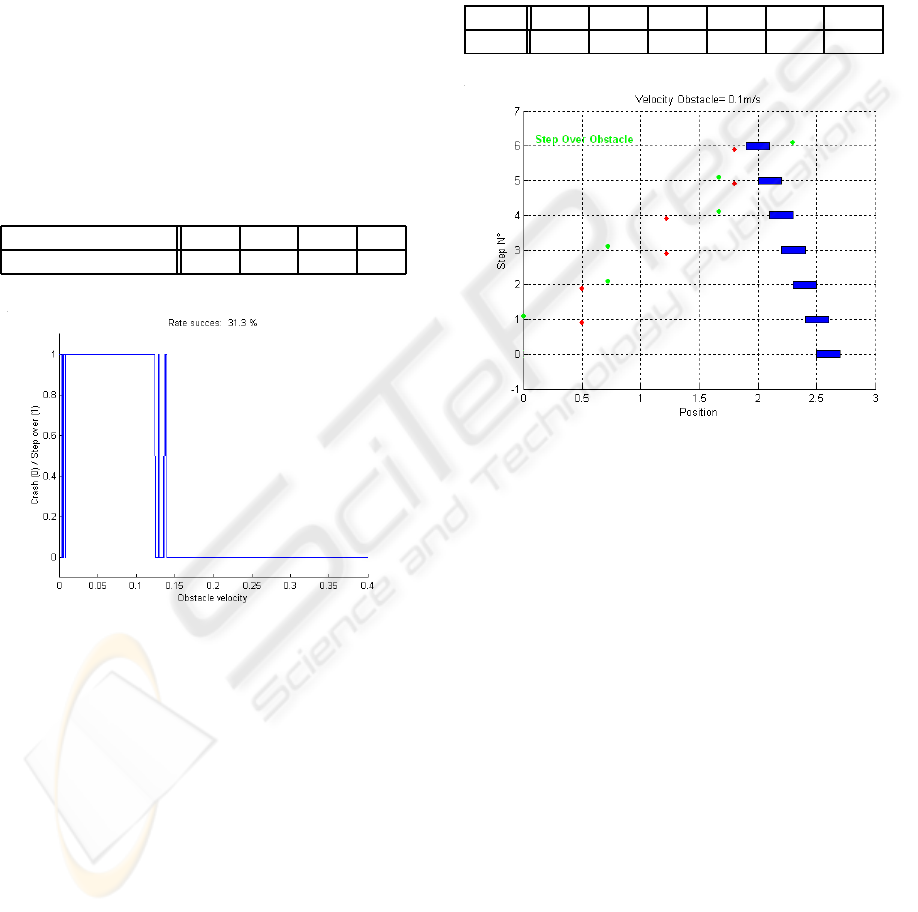
Table 1 gives results about successes rate for four
sizes of the obstacle. The rate success corresponds
to the ratio between the number of successes and the
totality of trials (1000). And the figure 3 shows an
example of the repartition between the successes and
the failures over an input range v
obs
and when L
obs
is equal to 0.2m. When the robot can step over the
obstacle successfully, the results is 1 otherwise it is 0.
Table 1: Rate success according to obstacle size.
Size (m) 0.1 0.2 0.3 0.4
Successes rate (%) 65.6 31.3 21.7 4.8
Figure 3: Successes rate when the size of the obstacle is
equal to 0.2m.
It must be pointed out that more the size is large,
more the successes rate is weak. And like figure 3
shows it, there is a threshold (0.12m/s approxima-
tively when L
obs
= 0.2m) where our footstep planning
never finds a solution. Consequently, the velocity of
the obstacle must be limited if we want the biped
crosses the obstacle successfully.
4.2 Footstep Planning Examples
Figure 4 shows a footstep sequence when the robot
crosses an obstacle. The size of the obstacle is equal
to 0.2m and its velocity is constant during all the sim-
ulation. Rectangles indicate the obstacle and the spots
indicate the two positions of the feet (left and right)
for each step. Table 2 gives the step length for all
the steps. It must be pointed out that when the biped
robot is close to the obstacle, then the length of the
step decreases in order to prepare the stepping over.
Finally, the last step allows to avoid obstacle without
collision.
Table 2: Length of the step L
step
when v
obs
= 0.1m/s and
L
obs
= 0.2m.
Step 1 2 3 4 5 6
L
step
0.50 0.22 0.50 0.45 0.13 0.50
Figure 4: Successful footstep planning when v
obs
= 0.1m/s
and L
obs
= 0.2m.
It is pertinent to note that one of the most inter-
esting point in our approach is its abilities to operate
when the velocity of the obstacle is not constant. Fig-
ure 5 shows the footstep sequence when the obstacle
moves with a random velocity. The velocity of the
obstacle is carried out by the sum of a constant value
which is equal to 0.1m/s and a random value included
into [−0.1..0.1]m/s. Table 3 gives V
obs
and L
step
for
each step. The size of the obstacle is equal to 0.1m.
It must be pointed out that the control strategy allows
to adapt automatically the length of the step accord-
ing to the obstacle velocity thanks to FQL algorithm.
For 1000 trials realized in the same conditions, the
successes rate is equal to 85% approximatively. This
is very interesting because our strategy allows to in-
crease the robustness of the footstep planning.
5 CONCLUSIONS
In this paper we have presented a footstep planning
strategy for biped robots allowing them to step over
FOOTSTEP PLANNING FOR BIPED ROBOT BASED ON FUZZY Q-LEARNING APPROACH
187
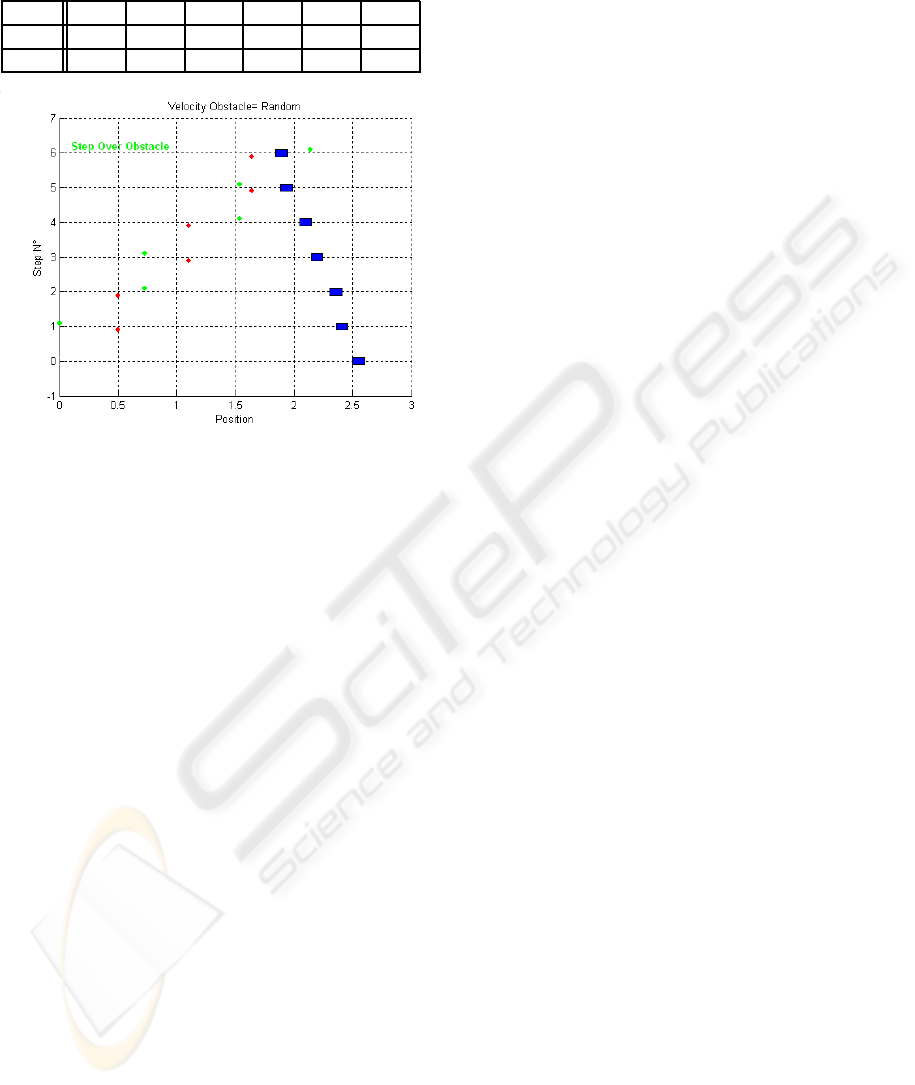
Table 3: Length of the step when v
obs
is random and L
obs
=
0.1m.
Step 1 2 3 4 5 6
v
obs
0.14 0.05 0.16 0.10 0.16 0.04
L
step
0.50 0.23 0.37 0.44 0.10 0.50
Figure 5: successful footstep planning when v
obs
is random,
L
obs
= 0.1m.
dynamic obstacles. Our footstep planning tactic is
based on a fuzzy Q-learning concept. The most ap-
pealing interest of our approach is its outstanding ro-
bustness related to the fact that the proposed footstep
planning is operational for both constant and variable
velocity of the obstacle.
Futures works will be focus on the improvement
of our footstep planning strategy:
• First, our actual control strategy does not take into
account the duration of the step. However, this
parameter is very important with dynamic obsta-
cles. Therefore, our goal is to enhance the pro-
posal footstep planning in order to take care about
both the length and the duration of the step,
• Second, in some cases, biped robot can not step
over obstacle: for example when the size of the
obstacle is too large. Consequently, the footstep
planning must be able to propose a path planning
in order to make the robot avoid obstacle.
• Third, in long-term, our goal is to design more
general footstep planning based on both local
footstep planning and global path planning,
• Finally, experimental validation may be consider
on real humanoid robot. But in this case, it is nec-
essary to design the joint trajectories based on the
position of feet.
REFERENCES
M. Hackel. Humanoid Robots: Human-like Machines. I-
Tech Education and Publishing, Vienna, Austria, June
2007 .
A. Carlos, P. Filho. Humanoid Robots: New Developments.
I-Tech Education and Publishing, Vienna, Austria,
June 2007.
Y. Ayza, K. Munawar, M. B. Malik, A. Konno and
M. Uchiyama. A Human-Like Approach to Footstep
Planning. Humanoid Robots, I-Tech Education and
Publishing, Vienna, Austria, June 2007, pp.296–314
J. Chestnutt, J. J. Kuffner. A Tiered Planning Strategy for
Biped Navigation. Int. Conf. on Humanoid Robots
(Humanoids’04), Santa Monica, California, 2004.
K. Sabe, M. Fukuchi, J.Gutmann, T. Ohashi, K. Kawamoto,
and T. Yoshigahara. Obstacle Avoidance and Path
Planning for Humanoid Robots using Stereo Vision.
Int. Conf. on Robotics Automation (ICRA). 2004, 592–
597.
J.J. Kuffner, K. Nishiwaki, S. Kagami, M. Inaba, H. In-
oue. Footstep Planning Among Obstacles for Biped
Robots. Proceedings of IEEE/RSJ Int. Conf. on Intel-
ligent Robots and Systems (IROS), 2001, 500–505.
J.J. Kuffner, K. Nishiwaki, S. Kagami, M. Inaba, H. Inoue.
Online Footstep Planning for Humanoid Robots. Pro-
ceedings of IEEE/RSJ Int. Conf. on Robotics and Au-
tomation (ICRA), 2003, 932–937
J. Chestnutt, M. Lau, G. Cheung, J.J. Kuffner, J. Hodgins, T.
Kanade. Footstep Planning for the Honda Asimo Hu-
manoid. Proceedings of IEEE Int. Conf. on Robotics
Automation (ICRA), 2005, pp. 629-634
C. Watkins, P. Dayan. Q-learning. Machine Learning, 8,
1992, 279–292.
R.S. Sutton, A.G. Barto. Reinforcement Learning: An In-
troduction. MIT Press, Cambridge, MA, 1998.
P. Y. Glorennec. Reinforcement Learning: an Overview. Eu-
ropean Symposium on Intelligent Techniques (ESIT),
2000,17–35.
P.Y. Glorennec, L. Jouffe. Fuzzy Q-Learning Proc. of
FUZZ-IEEE’97, Barcelona, 1997.
L. Jouffe. Fuzzy inference system learning by reinforce-
ment methods. IEEE Trans. on SMC, Part C, August
1998, Vol. 28 (3).
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
188
