FAIR AND EFFICIENT RESOURCE ALLOCATION

Bicriteria Models for Equitable Optimization

Włodzimierz Ogryczak

Institute of Control & Computation Engineering, Warsaw University of Technology, Nowowiejska 15/19, Warsaw, Poland

Keywords:

Optimization, multiple criteria, efﬁciency, fairness, equity, resource allocation.

Abstract:

Resource allocation problems are concerned with the allocation of limited resources among competing ac-

tivities so as to achieve the best performances. In systems which serve many usersthere is a need to respect

some fairness rules while looking for the overall efﬁciency. The so-called Max-Min Fairness is widely used to

meet these goals. However, allocating the resource to optimize the worst performance may cause a dramatic

worsening of the overall system efﬁciency. Therefore, several other fair allocation schemes are searched and

analyzed. In this paper we focus on mean-equity approaches which quantify the problem in a lucid form of two

criteria: the mean outcome representing the overall efﬁciency and a scalar measure of inequality of outcomes

to represent the equity (fairness) aspects. The mean-equity model is appealing to decision makers and allows

a simple trade-off analysis. On the other hand, for typical dispersion indices used as inequality measures, the

mean-equity approach may lead to inferior conclusions with respect to the outcomes maximization (system

efﬁciency). Some inequality measures, however, can be combined with the mean itself into optimization cri-

teria that remain in harmony with both inequality minimization and maximization of outcomes. In this paper

we introduce general conditions for inequality measures sufﬁcient to provide such an equitable consistency.

We verify the conditions for the basic inequality measures thus showing how they can be used not leading to

inferior distributions of system outcomes.

1 INTRODUCTION

Resource allocation problems are concerned with the

allocation of limited resources among competing ac-

tivities (Ibaraki and Katoh, 1988). In this paper, we

focus on approaches that, while allocating resources

to maximize the system efﬁciency, they also attempt

to provide a fair treatment of all the competing ac-

tivities (Luss, 1999). The problems of efﬁcient and

fair resource allocation arise in various systems which

serve many users, like in telecommunication systems

among others. In networking a central issue is how

to allocate bandwidth to ﬂows efﬁciently and fairly

(Bonald and Massoulie, 2001; Denda et al., 2000;

Kleinberg et al., 2001; Pi´oro and Medhi, 2004). In

location analysis of public services, the decisions of-

ten concern the placement of a service center or an-

other facility in a position so that the users are treated

fairly in an equitable way, relative to certain criteria

(Ogryczak, 2000). Recently, several research publica-

tions relating the fairness and equity concepts to the

multiple criteria optimization methodology have ap-

peared (Kostreva et al., 2004; Luss, 1999).

The generic resource allocation problem may be

stated as follows. Each activity is measured by an

individual performance function that depends on the

corresponding resource level assigned to that activ-

ity. A larger function value is considered better, like

the performance measured in terms of quality level,

capacity, service amount available, etc. Models with

an (aggregated) objective function that maximizes the

mean (or simply the sum) of individual performances

are widely used to formulate resource allocation prob-

lems, thus deﬁning the so-called mean solution con-

cept. This solution concept is primarily concerned

with the overall system efﬁciency. As based on aver-

aging, it often provides solution where some smaller

services are discriminated in terms of allocated re-

sources. An alternative approach depends on the so-

called Max-Min solution concept, where the worst

performance is maximized. The Max-Min approach

is consistent with Rawlsian (Rawls, 1971) theory of

justice, especially when additionally regularized with

the lexicographic order. The latter is called the Max-

149

Ogryczak W. (2008).

FAIR AND EFFICIENT RESOURCE ALLOCATION - Bicriteria Models for Equitable Optimization.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 149-156

DOI: 10.5220/0001485601490156

 SciTePress

Min Fairness (MMF) and commonly used in network-

ing (Pi´oro and Medhi, 2004; Ogryczak et al., 2005).

Allocating the resources to optimize the worst perfor-

mances may cause, however, a large worsening of the

overall (mean) performances. Therefore, there is a

need to seek a compromise between the two extreme

approaches discussed above.

Fairness is, essentially, an abstract socio-political

concept that implies impartiality, justice and equity

(Rawls and Kelly, 2001; Young, 1994), Neverthe-

less, fairness was frequently quantiﬁed with the so-

called inequality measures to be minimized (Atkin-

son, 1970; Rothschild and Stiglitz, 1973). Unfortu-

nately, direct minimization of typical inequality mea-

sures contradicts the maximization of individual out-

comes and it may lead to inferior decisions. In or-

der to ensure fairness in a system, all system entities

have to be equally well provided with the system’s

services. This leads to concepts of fairness expressed

by the equitable efﬁciency (Kostreva and Ogryczak,

1999; Luss, 1999). The concept of equitably efﬁ-

cient solution is a speciﬁc reﬁnement of the Pareto-

optimality taking into account the inequality mini-

mization according to the Pigou-Dalton approach. In

this paper the use of scalar inequality measures in bi-

criteria models to search for fair and efﬁcient allo-

cations is analyzed. There is shown that properties

of convexity and positive homogeneity together with

some boundedness condition are sufﬁcient for a typi-

cal inequality measure to guarantee that it can be used

consistently with the equitable optimization rules.

2 EQUITY AND FAIRNESS

The generic resource allocation problem may be

stated as follows. There is a system dealing with a set

I of m services. There is given a measure of ser-

vices realization within a system. In applications we

consider, the measure usually expresses the service

quality. In general, outcomes can be measured (mod-

eled) as service time, service costs, service delays as

well as in a more subjective way. There is also given

a set Q of allocation patterns (allocation decisions).

For each service i ∈ I a function f

(x) of the alloca-

tion pattern x ∈ Q has been deﬁned. This function,

called the individual objective function, measures the

outcome (effect) y

= f

(x) of allocation x pattern for

service i. In typical formulations a larger value of the

outcome means a better effect (higher service qual-

ity or client satisfaction). Otherwise, the outcomes

can be replaced with their complements to some large

number. Therefore, without loss of generality, we can

assume that each individual outcome y

is to be max-

imized which allows us to view the generic resource

allocation problem as a vector maximization model:

max {f(x) : x ∈ Q} (1)

where f(x) is a vector-function that maps the decision

space X = R

into the criterion space Y = R

, and

Q ⊂ X denotes the feasible set.

Model (1) only speciﬁes that we are interested in

maximization of all objective functions f

for i ∈ I =

{1,2,...,m}. In order to make it operational, one

needs to assume some solution concept specifying

what it means to maximize multiple objective func-

tions. The solution concepts may be deﬁned by prop-

erties of the corresponding preference model. The

preference model is completely characterized by the

relation of weak preference, denoted hereafter with

. Namely, the corresponding relations of strict pref-

erence ≻ and indifference

∼

are deﬁned by the fol-

lowing formulas:

′

≻ y

′′

⇔ (y

′

 y

′′

and y

′′

6 y

′

∼

′′

⇔ (y

′

 y

′′

and y

′′

 y

′

The standard preference model related to the Pareto-

optimal (efﬁcient) solution concept assumes that the

preference relation  is reﬂexive:

y  y, (2)

transitive:

′

 y

′′

and y

′′

 y

′′′

) ⇒ y

′

 y

′′′

, (3)

and strictly monotonic:

y+ εe

≻ y for ε > 0; i = 1,...,m, (4)

where e

denotes the i–th unit vector in the criterion

space. The last assumption expresses that for each in-

dividual objective function more is better (maximiza-

tion). The preference relations satisfying axioms (2)–

(4) are called hereafter rational preference relations.

The rational preference relations allow us to formal-

ize the Pareto-optimality (efﬁciency) concept with the

following deﬁnitions. We say that outcome vector y

′

rationally dominates y

′′

′

≻

′′

), iff y

′

≻ y

′′

for all

rational preference relations . We say that feasible

solution x ∈ Q is a Pareto-optimal (efﬁcient) solution

of the multiple criteria problem (1), iff y = f(x) is ra-

tionally nondominated.

Simple solution concepts for multiple criteria

problems are deﬁned by aggregation (or utility) func-

tions g : Y → R to be maximized. Thus the multiple

criteria problem (1) is replaced with the maximization

problem

max {g(f(x)) : x ∈ Q} (5)

In order to guarantee the consistency of the aggre-

gated problem (5) with the maximization of all indi-

vidual objective functions in the original multiple cri-

teria problem (or Pareto-optimality of the solution),

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

150

the aggregation function must be strictly increasing

with respect to every coordinate.

The simplest aggregation functions commonly

used for the multiple criteria problem (1) are deﬁned

as the mean (average) outcome

µ(y) =

∑

i=1

(6)

or the worst outcome

M(y) = min

i=1,...,m

. (7)

The mean (6) is a strictly increasing function while

the minimum (7) is only nondecreasing. Therefore,

the aggregation (5) using the sum of outcomes always

generates a Pareto-optimal solution while the maxi-

mization of the worst outcome may need some addi-

tional reﬁnement. The mean outcome maximization

is primarily concerned with the overall system efﬁ-

ciency. As based on averaging, it often provides a so-

lution where some services are discriminated in terms

of performances. On the other hand, the worst out-

come maximization, ie, the so-called Max-Min solu-

tion concept is regarded as maintaining equity. In-

deed, in the case of a simpliﬁed resource allocation

problem with the knapsack constraints, the Max-Min

solution meets the perfect equity requirement. In the

general case, with possibly more complex feasible

set structure, this property is not fulﬁlled. Never-

theless, if the perfectly equilibrated outcome vector

¯y

= ¯y

= ... = ¯y

is nondominated, then it is the

unique optimal solution of the corresponding Max-

Min optimization problem. In other words, the per-

fectly equilibrated outcome vector is a unique opti-

mal solution of the Max-Min problem if one cannot

ﬁnd any (possibly not equilibrated) vector with im-

proved at least one individual outcome without wors-

ening any others. Unfortunately, it is not a common

case and, in general, the optimal set to the Max-Min

aggregation may contain numerous alternative solu-

tions including dominated ones. The Max-Min solu-

tion may be then regularized according to the Rawl-

sian principle of justice (Rawls, 1971) which leads

us to the lexicographic Max-Min concepts or the so-

called Max-Min Fairness (Marchi and Oviedo, 1992;

Ogryczak and

Sliwi´nski, 2006).

In order to ensure fairness in a system, all sys-

tem entities have to be equally well provided with

the system’s services. This leads to concepts of fair-

ness expressed by the equitable rational preferences

(Kostreva and Ogryczak, 1999). First of all, the fair-

ness requires impartiality of evaluation, thus focusing

on the distribution of outcome values while ignoring

their ordering. That means, in the multiple criteria

problem (1) we are interested in a set of outcome val-

ues without taking into account which outcome is tak-

ing a speciﬁc value. Hence, we assume that the pref-

erence model is impartial (anonymous, symmetric).

In terms of the preference relation it may be written

as the following axiom

π(1)

,...,y

π(m)

)

∼

,...,y

) ∀π ∈ Π(I) (8)

where Π(I) denotes the set of all permutations of

I. This means that any permuted outcome vector is

indifferent in terms of the preference relation. Fur-

ther, fairness requires equitability of outcomes which

causes that the preference model should satisfy the

(Pigou–Dalton) principle of transfers. The principle

of transfers states that a transfer of any small amount

from an outcome to any other relatively worse–off

outcome results in a more preferred outcome vector.

As a property of the preference relation, the principle

of transfers takes the form of the following axiom

y−εe

+ εe

≻ y for 0 < ε < y

−y

(9)

The rational preference relations satisfying addition-

ally axioms (8) and (9) are called hereafter fair (equi-

table) rational preference relations. We say that out-

come vector y

′

fairly (equitably) dominates y

′′

′

≻

′′

), iff y

′

≻y

′′

for all fair rational preference relations

. In other words, y

′

fairly dominates y

′′

, if there

exists a ﬁnite sequence of vectors y

(j = 1,2,.. .,s)

such that y

= y

′′

, y

= y

′

and y

is constructed from

j− 1

by application of either permutation of coordi-

nates, equitable transfer, or increase of a coordinate.

An allocation pattern x ∈Q is called fairly (equitably)

efﬁcient or simply fair if y = f(x) is fairly nondomi-

nated. Note that each fairly efﬁcient solution is also

Pareto-optimal, but not vice verse.

In order to guarantee fairness of the solution con-

cept (5), additional requirements on the class of ag-

gregation (utility) functions must be introduced. In

particular, the aggregation function must be addition-

ally symmetric (impartial), i.e. for any permutation π

of I,

g(y

π(1)

π(2)

,... ,y

π(m)

) = g(y

,... ,y

) (10)

as well as be equitable (to satisfy the principle of

transfers)

g(y

,... ,y

−ε,... ,y

+ ε,... ,y

) > g(y

,...,y

)

(11)

for any 0 < ε < y

′

−y

′′

. In the case of a strictly

increasing function satisfying both the requirements

(10) and (11), we call the corresponding problem (5)

a fair (equitable) aggregation of problem (1). Every

optimal solution to the fair aggregation (5) of a multi-

ple criteria problem (1) deﬁnes some fair (equitable)

solution.

FAIR AND EFFICIENT RESOURCE ALLOCATION - Bicriteria Models for Equitable Optimization

151

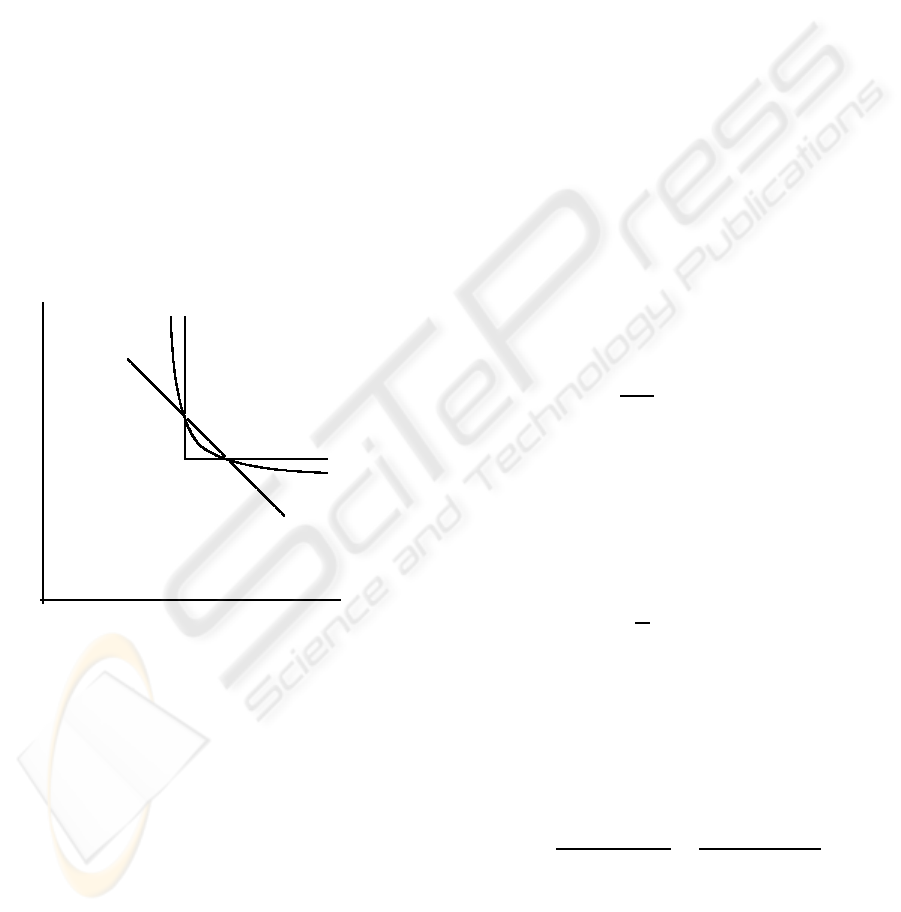
Note that both the simplest aggregation functions,

the sum (6) and the minimum (7), are symmetric al-

though they do not satisfy the equitability require-

ment (11). To guarantee the fairness of solutions,

some enforcement of concave properties is required.

For any strictly concave, increasing utility function

u : R → R, the function g(y) =

∑

i=1

u(y

) is a strictly

monotonic and equitable thus deﬁning a family of the

fair aggregations. Various concave utility functions

u can be used to deﬁne such fair solution concepts.

In the case of the outcomes restricted to positive val-

ues, one may use logarithmic function thus resulting

in the Proportional Fairness (PF) solution concept

(Kelly et al., 1997). Actually, it corresponds to the

so-called Nash criterion which maximizes the product

of additional utilities compared to the status quo. For

a common case of upper bounded outcomes y

≤ y

∗

one may maximize power functions −

∑

i=1

∗

−y

)

for 1 < p < ∞ which corresponds to the minimization

of the corresponding p-norm distances from the com-

mon upper bound y

∗

(Kostreva et al., 2004).

¯y



= y



S(¯y)

D(¯y)

u(y) = u(¯y)

Figure 1: Structure of the fair dominance: D(¯y) – the set

fairly dominated by ¯y, S(¯y) – the set of outcomes fairly

dominating ¯y.

Fig. 1 presents the structure of fair dominance for

two-dimensional outcome vectors. For any outcome

vector ¯y, the fair dominance relation distinguishes set

D(¯y) of dominated outcomes (obviously worse for all

fair rational preferences) and set S(¯y) of dominating

outcomes (obviously better for all fair rational prefer-

ences). However, some outcome vectors are left (in

white areas) and they can be differently classiﬁed by

various speciﬁc fair rational preferences. The MMF

fairness assigns the entire interior of the inner white

triangle to the set of preferred outcomes while clas-

sifying the interior of the external open triangles as

worse outcomes. Isolines of various utility functions

split the white areas in different ways. One may no-

tice that the set D(¯y) of directions leading to outcome

vectors being dominated by a given ¯y is, in general,

not a cone and it is not convex. Although, when we

consider the set S(¯y) of directions leading to outcome

vectors dominating given ¯y we get a convex set.

3 INEQUALITY MEASURES AND

FAIR CONSISTENCY

Inequality measures were primarily studied in eco-

nomics while recently they become very popular tools

in Operations Research. Typical inequality mea-

sures are some deviation type dispersion characteris-

tics. They are translation invariant in the sense that

ρ(y+ νe) = ρ(y) for any outcome vector y and real

number ν (where e vector of units (1,...,1)), thus

being not affected by any shift of the outcome scale.

Moreover, the inequality measures are also inequality

relevant which means that they are equal to 0 in the

case of perfectly equal outcomeswhile taking positive

values for unequal ones.

The simplest inequality measures are based on the

absolute measurement of the spread of outcomes, like

the mean absolute difference

Γ(y) =

∑

i=1

∑

j=1

−y

| (12)

or the maximum absolute difference

d(y) = max

i, j=1,...,m

−y

| (13)

In most application frameworksbetter intuitive appeal

may have inequality measures related to deviations

from the mean outcome like the mean absolute de-

viation

δ(y) =

∑

i=1

−µ(y)| (14)

or the maximum absolute deviation

R(y) = max

i∈I

−µ(y)| (15)

Note that the standard deviation σ (or the variance

) represents both the deviations and the spread mea-

surement as

(y) =

∑

i∈I

−µ(y))

∑

i∈I

∑

j∈I

−y

)

(16)

Deviational measures may be focused on the down-

side semideviations as related to worsening of out-

come while ignoring upper semideviations related to

improvement of outcome. One may deﬁne the maxi-

mum (downside) semideviation

∆(y) = max

i∈I

(µ(y) −y

) (17)

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

152

and the mean (downside) semideviation

δ(y) =

∑

i∈I

(µ(y) −y

)

(18)

where (.)

denotes the nonnegative part of a num-

ber. Similarly, the standard (downside) semideviation

is given as

σ(y) =

∑

i∈I

(µ(y) −y

)

(19)

In economics one usually considers relative inequal-

ity measures normalized by mean outcome. Among

many inequality measures perhaps the most com-

monly accepted by economists is the Gini coefﬁcient,

which is the relative mean difference. One can easily

notice that direct minimization of typical inequality

measures (especially the relative ones) may contra-

dict the optimization of individual outcomes resulting

in equal but very low outcomes. As some resolution

one may consider a bicriteria mean-equity model:

max {(µ(f(x)),−ρ(f(x))) : x ∈ Q} (20)

which takes into account both the efﬁciency with op-

timization of the mean outcome µ(y) and the eq-

uity with minimization of an inequality measure ρ(y).

For typical inequality measures bicriteria model (20)

is computationally very attractive since both the cri-

teria are concave and LP implementable for many

measures. Unfortunately, for any dispersion type in-

equality measures the bicriteria mean-equity model

is not consistent with the outcomes maximization,

and therefore is not consistent with the fair domi-

nance. When considering a simple discrete problem

with two allocation patterns P1 and P2 generating

outcome vectors y

′

= (0, 0) and y

′′

= (2,8), respec-

tively, for any dispersion type inequality measure one

gets ρ(y

′′

) > 0 = ρ(y

′

) while µ(y

′′

) = 5 > 0 = µ(y

′

Hence, y

′′

is not bicriteria dominated by y

′

and vice

versa. Thus for any dispersion type inequality mea-

sure ρ, allocation P1 with obviously worse outcome

vector than that for allocation P2 is a Pareto-optimal

solution in the corresponding bicriteria mean-equity

model (20).

Note that the lack of consistency of the mean-

equity model (20) with the outcomes maximization

applies also to the case of the maximum semidevia-

tion ∆(y) (17) used as an inequality measure whereas

subtracting this measure from the mean µ(y)−∆(y) =

M(y) results in the worst outcome and thereby the

ﬁrst criterion of the MMF model. In other words, al-

though a direct use of the maximum semideviation in

the mean-equity model may contradict the outcome

maximization, the measure can be used complemen-

tary to the mean leading us to the worst outcome cri-

terion which does not contradict the outcome max-

imization. This construction can be generalized for

various (dispersion type) inequality measures. More-

over, we allowthe measures to be scaled with any pos-

itive factor α > 0, in order to avoid creation of new

inequality measures as one could consider ρ

(X) =

αρ(X) as a different inequality measure. For any in-

equality measure ρ we introduce the corresponding

underachievement function deﬁned as the difference

of the mean outcome and the (scaled) inequality mea-

sure itself, i.e.

αρ

(y) = µ(y) −αρ(y). (21)

This allows us to replace the original mean-equity bi-

criteria optimization (20) with the following bicriteria

problem:

max{(µ(f(x)),µ(f(x)) −αρ(f(x))) : x ∈Q} (22)

where the second objective represents the correspond-

ing underachievement measure M

αρ

(y) (21). Note

that for any inequality measure ρ(y) ≥ 0 one gets

αρ

(y) ≤ µ(y) thus really expressing underachieve-

ments (comparing to mean) from the perspective of

outcomes being maximized.

We will say that an inequality measure ρ is fairly

α-consistent if

′



′′

⇒ µ(y

′

) −αρ(y

′

) ≥ µ(y

′′

) −αρ(y

′′

) (23)

The relation of fair α-consistency will be called

strong if, in addition to (23), the following holds

′

≻

′′

⇒ µ(y

′

) −αρ(y

′

) > µ(y

′′

) −αρ(y

′′

). (24)

Theorem 1. If the inequality measure ρ(y) is fairly

α-consistent (23), then except for outcomes with iden-

tical values of µ(y) and ρ(y), every efﬁcient solution

of the bicriteria problem (22) is a fairly efﬁcient allo-

cation pattern. In the case of strong consistency (24),

every allocation pattern x ∈ Q efﬁcient to (22) is, un-

conditionally, fairly efﬁcient.

Proof. Let x

∈ Q be an efﬁcient solution of (22).

Suppose that x

is not fairly efﬁcient. This means,

there exists x ∈ Q such that y = f(x) ≻

= f(x

Then, it follows µ(y) ≥ µ(y

), and simultaneously

µ(y) −αρ(y) ≥ µ(y

) −αρ(y

), by virtue of the fair

α-consistency (23). Since x

is efﬁcient to (22) no in-

equality can be strict, which implies µ(y) = µ(y

) and

and ρ(y) = ρ(y

In the case of the strong fair α-consistency (24),

the supposition y = f(x) ≻

= f(x

) implies µ(y) ≥

µ(y

) and µ(y)−αρ(y) > µ(y

)−αρ(y

) which con-

tradicts the efﬁciency of x

with respect to (22).

Hence, the allocation pattern x

is fairly efﬁcient.

FAIR AND EFFICIENT RESOURCE ALLOCATION - Bicriteria Models for Equitable Optimization

153

4 FAIR CONSISTENCY

CONDITIONS

Typical dispersion type inequality measures are con-

vex, i.e. ρ(λy

′

+ (1 −λ)y

′′

) ≤ λρ(y

′

) + (1−λ)ρ(y

′′

)

for any y

′

′′

and 0 ≤ λ ≤ 1. Certainly, the under-

achievementfunction M

αρ

(y) must be also monotonic

for the fair consistency which enforces more restric-

tions on the inequality measures. We will show fur-

ther that convexity together with positive homogene-

ity and some boundedness of an inequality measure

is sufﬁcient to guarantee monotonicity of the corre-

sponding underachievement measure and thereby to

guarantee the fair α-consistency of inequality mea-

sure itself.

We say that (dispersion type) inequality measure

ρ(y) ≥ 0 is ∆-bounded if it is upper bounded by the

maximum downside deviation, i.e.,

ρ(y) ≤ ∆(y) ∀y. (25)

Moreover, we say that ρ(y) ≥ 0 is strictly ∆-bounded

if inequality (25) is a strict bound, except from the

case of perfectly equal outcomes, i.e., ρ(y) < ∆(y)

for any y such that ∆(y) > 0.

Theorem 2. Let ρ(y) ≥ 0 be a convex, positively

homogeneous and translation invariant (dispersion

type) inequality measure. If αρ(y) is ∆-bounded, then

ρ(y) is fairly α-consistent in the sense of (23).

Proof. The relation of fair dominance y

′



′′

de-

notes that there exists a ﬁnite sequence of vectors

= y

′′

,... ,y

such that y

= y

k−1

−ε

′

+ ε

′′

0 ≤ε

≤y

k−1

′

−y

k−1

′′

for k = 1,2,.. .,t and there exists

a permutation π such that y

′

π(i)

≥ y

for all i ∈I. Note

that the underachievement function M

αρ

(y), similar

as ρ(y) depends only on the distribution of outcomes.

Further, if y

′

≥ y

′′

, then y

′

= y

′′

+ (y

′

−y

′′

) and y

′

−

′′

≥ 0. Hence, due to concavity and positive homo-

geneity, M

αρ

′

) ≥ M

αρ

′′

) + M

αρ

′

−y

′′

). More-

over, due to the bound (25), M

αρ

′

−y

′′

) ≥ µ(y

′

−

′′

) −∆(y

′

−y

′′

) ≥ µ(y

′

−y

′′

) −µ(y

′

−y

′′

) = 0. Thus,

αρ

(y) satisﬁes also the requirement of monotonic-

ity. Hence, M

αρ

′

) ≥ M

αρ

). Further, let us notice

that y

= λ

k−1

+ (1−λ)y

k−1

where

k−1

= y

k−1

−

′

−y

′′

′

+ (y

′

−y

′′

and λ = ε/(y

′

−y

′′

). Vec-

tor

k−1

has the same distribution of coefﬁcients as

k−1

(actually it represents results of swapping y

′

and y

′′

). Hence, due to concavity of M

αρ

(y), one

gets M

αρ

) ≥ λM

αρ

(

k−1

) + (1 −λ)M

αρ

k−1

) =

αρ

k−1

). Thus, M

αρ

′

) ≥ M

αρ

′′

) which justiﬁes

the fair α-consistency of ρ(y).

For strong fair α-consistency some strict

monotonicity and concavity properties of the un-

derachievement function are needed. Obviously,

there does not exist any inequality measure which is

positively homogeneous and simultaneously strictly

convex. However, one may notice from the proof

of Theorem 2 that only convexity properties on

equally distributed outcome vectors are important for

monotonous underachievement functions.

We say that inequality measure ρ(y) ≥0 is strictly

convex on equally distributed outcome vectors, if

ρ(λy

′

+ (1−λ)y

′′

) < λρ(y

′

) + (1−λ)ρ(y

′′

)

for 0 < λ < 1 and any two vectors y

′

6= y

′′

representing

the same outcomes distribution as some y, i.e., y

′

(1)

,... ,y

′

(m)

) π

′

and y

′′

= (y

′′

(1)

,... ,y

′′

(m)

) for

some permutations π

′

and π

′′

, respectively.

Theorem 3. Let ρ(y) ≥ 0 be a convex, positively

homogeneous and translation invariant (dispersion

type) inequality measure. If ρ(y) is also strictly con-

vex on equally distributed outcomes and αρ(y) is

strictly ∆-bounded, then the measure ρ(y) is fairly

strongly α-consistent in the sense of (24).

Proof. The relation of weak fair dominance y

′



′′

denotes that there exists a ﬁnite sequence of vectors

= y

′′

,... ,y

such that y

= y

k−1

−ε

′

+ ε

′′

0 ≤ε

≤y

k−1

′

−y

k−1

′′

for k = 1,2,.. .,t and there exists

a permutation π such that y

′

π(i)

≥ y

for all i ∈ I. The

strict fair dominance y

′

≻

′′

means that y

′

π(i)

> y

for

some i ∈ I or at least one ε

is strictly positive. Note

that the underachievement function M

αρ

(y) is strictly

monotonousand strictly convex on equally distributed

outcome vectors. Hence, M

αρ

′

) > M

αρ

′′

) which

justiﬁes the fair strong α-consistency of the measure

ρ(y).

The speciﬁc case of fair 1-consistency is also

called the mean-complementary fair consistency.

Note that the fair

α-consistency of measure ρ(y) ac-

tually guarantees the mean-complementary fair con-

sistency of measure αρ(y) for all 0 < α ≤

α, and the

same remain valid for the strong consistency proper-

ties. It follows from a possible expression of µ(y) −

αρ(y) as the convex combination of µ(y)−

αρ(y) and

µ(y). Hence, for any y

′



′′

, due to µ(y

′

) ≥ µ(y

′′

)

one gets µ(y

′

) −αρ(y

′

) ≥ µ(y

′′

) −αρ(y

′′

) in the case

of the fair

α-consistency of measure ρ(y) (or respec-

tive strict inequality in the case of strong consistency).

Therefore, while analyzing speciﬁc inequality mea-

sures we seek the largest values α guaranteeing the

corresponding fair consistency.

As mentioned, typical inequality measures are

convex and many of them are positively homoge-

neous. Moreover, the measures such as the mean ab-

solute (downside) semideviation

δ(y) (18), the stan-

dard downside semideviation

σ(y) (19), and the mean

absolute difference Γ(y) (12) are ∆-bounded. Indeed,

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

154

one may easily notice that µ(y)−y

≤∆(y) and there-

fore

δ(y) ≤

∑

i∈I

∆(y) = ∆(y),

σ(y) ≤

∆(y)

∆(y) and Γ(y) =

∑

i∈I

∑

j∈I

(max{y

}−µ(y)) ≤

∆(y). Actually, all these inequality measures are

strictly ∆-bounded since for any unequal outcome

vector at least one outcome must be below the

mean thus leading to strict inequalities in the above

bounds. Obviously, ∆-bounded (but not strictly) is

also the maximum absolute downside deviation ∆(y)

itself. This allows us to justify the maximum down-

side deviation ∆(y) (17), the mean absolute (down-

side) semideviation

δ(y) (18), the standard down-

side semideviation

σ(y) (19) and the mean absolute

difference Γ(y) (12) as fairly 1-consistent (mean-

complementary fairly consistent) in the sense of (23).

We emphasize that, despite the standard semide-

viation is a fairly 1-consistent inequality measure, the

consistency is not valid for variance, semivariance

and even for the standard deviation. These measures,

in general, do not satisfy the all assumptions of The-

orem 2. Certainly, we have enumerated only the sim-

plest inequality measures studied in the resource allo-

cation context which satisfy the assumptions of The-

orem 2 and thereby they are fairly 1-consistent. The-

orem 2 allows one to show this property for many

other measures. In particular, one may easily ﬁnd

out that any convex combination of fairly α-consistent

inequality measures remains also fairly α-consistent.

On the other hand, among typical inequality measures

the mean absolute difference seems to be the only one

meeting the stronger assumptions of Theorem 3 and

thereby maintaining the strong consistency.

As mentioned, the mean absolute deviation is

twice the mean absolute downside semideviation

which means that αδ(y) is ∆-boundedfor any 0 < α ≤

0.5. The symmetry of mean absolute semideviations

δ(y) =

∑

i∈I

−µ(y))

∑

i∈I

(µ(y) −y

)

can be

also used to derive some ∆-boundedness relations for

other inequality measures. In particular, one may ﬁnd

out that for m-dimensional outcome vectors of un-

weighted problem, any downside semideviation from

the mean cannot be larger than m−1 upper semidevi-

ations. Hence, the maximum absolute deviation satis-

ﬁes the inequality

m−1

R(y) ≤ ∆(y), while the maxi-

mum absolute difference fulﬁlls

d(y) ≤∆(y). Simi-

larly, for the standard deviation one gets

√

m−1

δ(y) ≤

∆(y). Actually, ασ(y) is strictly ∆-bounded for any

0 < α ≤ 1/

√

m−1 since for any unequal outcome

vector at least one outcome must be below the mean

thus leading to strict inequalities in the above bounds.

These allow us to justify the mean absolute semidevi-

ation with 0 < α ≤ 0.5, the maximum absolute devia-

tion with 0 < α ≤

m−1

, the maximum absolute differ-

ence with 0 < α ≤

and the standard deviation with

0 < α ≤

√

m−1

as fairly α-consistent within the spec-

iﬁed intervals of α. Moreover, the α-consistency of

the standard deviation is strong.

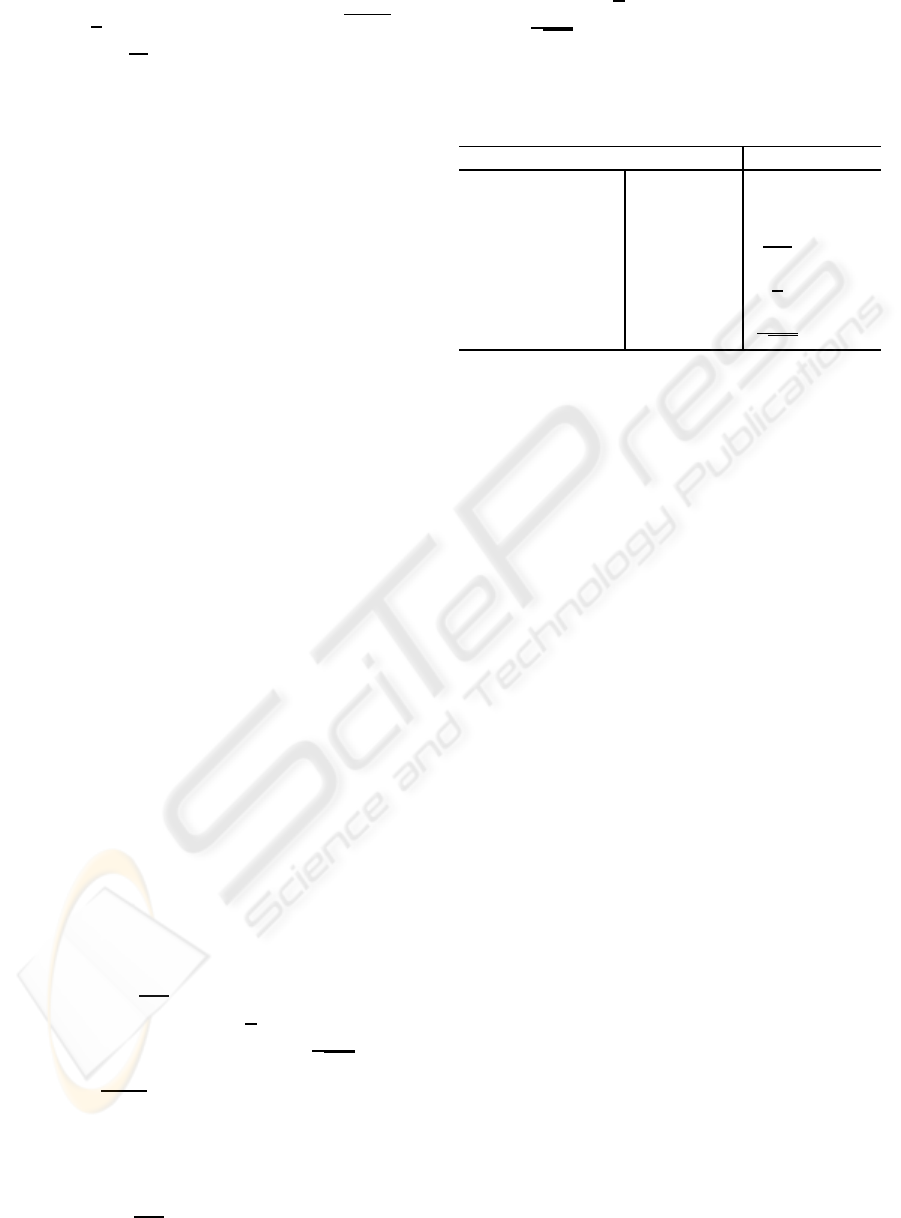
Table 1: Fair consistency results.

Measure α–consistency

Mean abs. semidev.

δ(y) (18)

Mean abs. dev.

δ(y) (14) 0.5

Max. semidev.

∆(y) (17) 1

Max. abs. dev. R(y) (15)

m−1

Mean abs. diff.

Γ(y) (12) 1 strong

Max. abs. diff.

d(y) (13)

Standard semidev.

σ(y) (19)

Standard dev. σ(y) (16)

√

m−1

strong

The fair consistency results for basic dispersion type

inequality measures considered in resource alloca-

tion problems are summarized in Table 1 where α

values are given and the strong consistency is indi-

cated. Table 1 points out how the inequality measures

can be used in resource allocation models to guar-

antee their harmony both with outcome maximiza-

tion (Pareto-optimality) and with inequalities mini-

mization (Pigou-Dalton equity theory). Exactly, for

each inequality measure applied with the correspond-

ing value α from Table 1 (or smaller positive value),

every efﬁcient solution of the bicriteria problem (22),

ie. max{(µ(f(x)),µ(f(x)) −αρ(f(x))) : x ∈ Q}, is a

fairly efﬁcient allocation pattern, except for outcomes

with identical values of µ(y) and ρ(y). In the case of

strong consistency (as for mean absolute difference or

standard deviation), every solution x ∈ Q efﬁcient to

(22) is, unconditionally, fairly efﬁcient.

The consistency results summarized in Table 1 are

sufﬁcient conditions. This means that whenever the α

limit is observed the corresponding consistency rela-

tion is valid for any problem. It may happen that for

a speciﬁc problem instance and a speciﬁc inequality

measure the fair consistency is valid for larger values

of α. Nevertheless, we have provided strict bounds

in the sense that for a larger value of α there exists a

resource allocation problem on which the fair consis-

tency is not valid, and the bicriteria problem (22) may

generate dominated solution.

5 CONCLUSIONS

The problems of efﬁcient and fair resource allocation

arise in various systems which serve many users. Fair-

ness is, essentially, an abstract socio-political concept

that implies impartiality, justice and equity. Neverthe-

FAIR AND EFFICIENT RESOURCE ALLOCATION - Bicriteria Models for Equitable Optimization

155

less, in operations research it was quantiﬁed with var-

ious solution concepts (Denda et al., 2000). The eq-

uitable optimization with the preference structure that

complies with both the efﬁciency (Pareto-optimality)

and with the Pigou-Dalton principle of transfers may

be used to formalize the fair solution concepts. Mul-

tiple criteria models equivalent to equitable optimiza-

tion allows to generate a variety of fair and efﬁcient

resource allocation patterns (Kostreva et al., 2004;

Ogryczak et al., 2008).

In this paper we haveanalyzed how scalar inequal-

ity measures can be used to guarantee the fair consis-

tency. It turns out that several inequality measures can

be combined with the mean itself into the optimiza-

tion criteria generalizing the concept of the worst out-

come and generating fairly consistent underachieve-

ment measures. We have shown that properties of

convexity and positive homogeneity together with be-

ing bounded by the maximum downside semidevia-

tion are sufﬁcient for a typical inequality measure to

guarantee the corresponding fair consistency. It al-

lows us to identify various inequality measures which

can be effectively used to incorporate fairness fac-

tors into various resource allocation problems while

preserving the consistency with outcomes maximiza-

tion. Among others, the standard semideviation and

the mean semideviation turn out to be such a consis-

tent inequality measure while the mean absolute dif-

ference is strongly consistent.

Our analysis is related to the properties of solu-

tions to resource allocation models. It has been shown

how inequality measures can be included into the

models avoiding contradiction to the maximization of

outcomes. We do not analyze algorithmic issues for

the speciﬁc resource allocation problems. Generally,

the requirement of convexity necessary for the consis-

tency, guarantees that the corresponding optimization

criteria belong to the class of convex optimization, not

complicating the original resource allocation model

with any additional discrete structure. Many of the in-

equality measures, we analyzed, can be implemented

with auxiliary linear programming constraints. Nev-

ertheless, further research on efﬁcient computational

algorithms for solving the speciﬁc models is neces-

sary.

REFERENCES

Atkinson, A. (1970). On the measurement of inequality. J.

Economic Theory, 2:244–263.

Bonald, T. and Massoulie, L. (2001). Impact of fairness on

internet performance. In Proceedings of ACM Sigmet-

rics, pages 82–91.

Denda, R., Banchs, A., and Effelsberg, W. (2000). The

fairness challenge in computer networks. Lect. Notes

Comp. Sci., 1922:208–220.

Ibaraki, T. and Katoh, N. (1988). Resource Allocation

Problems, Algorithmic Approaches. MIT Press, Cam-

bridge.

Kelly, F., Mauloo, A., and Tan, D. (1997). Rate con-

trol for communication networks: shadow prices, pro-

portional fairness and stability. J. Opnl. Res. Soc.,

49:206–217.

Kleinberg, J., Rabani, Y., and Tardos, E. (2001). Fairness

in routing and load balancing. J. Comput. Syst. Sci.,

63:2–21.

Kostreva, M. M. and Ogryczak, W. (1999). Linear opti-

mization with multiple equitable criteria. RAIRO Op-

erations Research, 33:275–297.

Kostreva, M. M., Ogryczak, W., and Wierzbicki, A. (2004).

Equitable aggregations and multiple criteria analysis.

Eur. J. Opnl. Res., 158:362–377.

Luss, H. (1999). On equitable resource allocation problems:

A lexicographic minimax approach. Operations Re-

search, 47:361–378.

Marchi, E. and Oviedo, J. A. (1992). Lexicographic op-

timality in the multiple objective linear programming:

the nucleolar solution. Eur. J. Opnl. Res., 57:355–359.

Ogryczak, W. (2000). Inequality measures and equitable

approaches to location problems. Eur. J. Opnl. Res.,

122:374–391.

Ogryczak, W., Pi´oro, M., and Tomaszewski, A. (2005).

Telecommunications network design and max-min

optimization problem. J. Telecom. Info. Tech., 3:1–14.

Ogryczak, W. and

Sliwi´nski, T. (2006). On direct methods

for lexicographic min-max optimization. Lect. Notes

Comp. Sci., 3982:774–783.

Ogryczak, W., Wierzbicki, A., and Milewski, M. (2008). A

multi-criteria approach to fair and efﬁcient bandwidth

allocation. OMEGA, 36:451–463.

Pi´oro, M. and Medhi, D. (2004). Routing, Flow and Ca-

pacity Design in Communication and Computer Net-

works. Morgan Kaufmann, San Francisco.

Rawls, J. (1971). The Theory of Justice. Harvard Univ.

Press, Cambridge.

Rawls, J. and Kelly, E. (2001). Justice as Fairness: A Re-

statement. Harvard Univ. Press, Cambridge.

Rothschild, M. and Stiglitz, J. E. (1973). Some further re-

sults in the measurement of inequality. J. Econ. The-

ory, 6:188–204.

Young, H. P. (1994). Equity in Theory and Practice. Prince-

ton Univ. Press, Princeton.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

156