PHASE

LOCKED LOOPS DESIGN AND ANALYSIS

Nikolay V. Kuznetsov, Gennady A. Leonov and Svetlana S. Seledzhi

Saint-Petersburg State University, Universitetski pr. 28, Saint-Petersburg, 198504, Russia

Keywords:

Mathematical model, stability, Phase-locked loops, Costas loop.

Abstract:

New methods, for the design of different block diagrams of PLL, using the asymphtotic analysis of high-

frequency periodic oscillations, are suggested. The PLL description on three levels is made: 1) on the level of

electronic realizations; 2) on the level of phase and frequency relations between inputs and outputs in block

diagrams; 3) on the level of differential and integro-differential equations. On the base of such description, the

block diagram of ﬂoating PLL for the elimination of clock skew and that of frequency synthesizer is proposed.

The rigorous mathematical formulation of the Costas loop for the clock oscillators are ﬁrst obtained. The

theorem on a PLL global stability is proved.

1 INTRODUCTION

The phase-locked loops are widespread in a mod-

ern radio electronics and circuit technology (Viterbi,

1966; Gardner, 1966; Lindsey, 1972; Lindsey and

Chie, 1981; Leonov, Reitmann and Smirnova, 1992;

Leonov, Ponomarenko and Smirnova, 1996; Leonov

and Smirnova, 2000; Kroupa, 2003; Best, 2003,

Razavi, 2003; Egan, 2000; Abramovitch, 2002). In

this paper the technique of PLL description on three

levels is suggested:

1) on the level of electronic realizations,

2) on the level of phase and frequency relations

between inputs and outputs in block-diagrams,

3) on the level of differential and integro-

differential equations.

The second level, involving the asymptotical anal-

ysis of high-frequency oscillations, is necessary for

the well-formed derivation of equations and for the

passage on the third level of description. For example,

the main for the PLL theory notion of phase detector

is formed exactly on the second level of consideration.

In this case the characteristic of phase detector de-

pends on the class of considered oscillations. While

in the classical PLL it is used the oscillation multi-

pliers, for harmonic oscillations, the characteristic of

phase detector is also harmonic, for the impulse os-

cillations (for the same electronic realization of feed-

back loop) it is a continuous piecewise-linear periodic

function.

In the present work the development of the above-

mentioned technique for PLL is pursued. Here for

the standard electronic realizations, the characteristics

of phase detectors are computed and the differential

equations, describing the PLL operation, are derived.

Here together with usual PLL the Costas loop is

also considered. The essential conclusion is that the

Costas loop with impulse oscillators tunes to a half

frequency of master oscillator.

2 BLOCK DIAGRAM AND

MATHEMATICAL MODEL OF

PLL

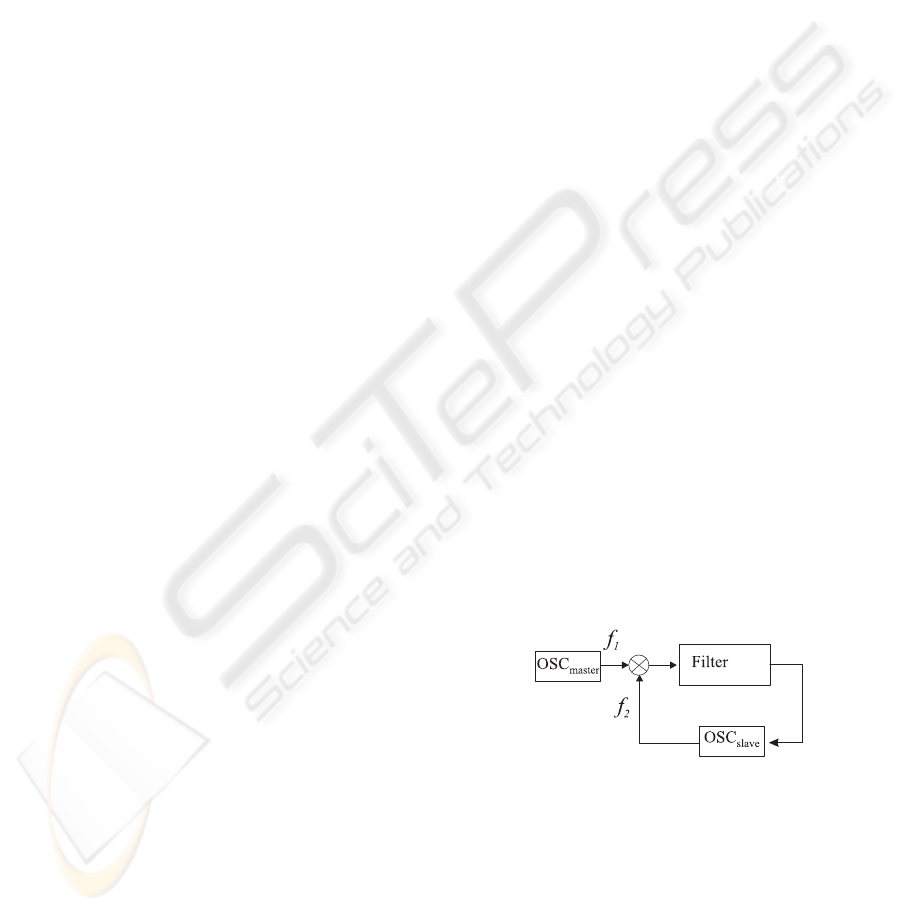
Consider a PLL on the ﬁrst level (Fig.1)

Figure

1: Electronic circuit of PLL.

Here OSC

master

is a master oscillator, OSC

slave

is a

slave oscillator, which generates high-frequency ”al-

most harmonic oscillations”

(t) = A

sin(ω

(t)t + ψ

). (1)

Block × is a multiplier of oscilations of f

(t) and

(t). At its output the signal f

(t) f

(t) arises. The

relations between the input ξ(t) and the output σ(t) of

114

Kuznetsov N., Leonov G. and Seledzhi S. (2008).

PHASE LOCKED LOOPS DESIGN AND ANALYSIS.

In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 114-118

DOI: 10.5220/0001485401140118

 SciTePress

linear ﬁlter have the form

σ(t) = α

(t) +

γ(t − τ)ξ(τ)dτ.

Here γ(t) is an impulse transient function of ﬁlter,

(t) is an exponentially damped function, depend-

ing on the initial date of ﬁlter at the moment t = 0.

Now we reformulate the high-frequency property

of oscillations f

(t) to obtain the following condition.

Consider the great ﬁxed time interval [0,T ], which

can be partitioned into small intervals of the form

[τ,τ + δ], (τ ∈ [0, T ]), where the following relations

|γ(t) − γ(τ)| ≤ Cδ, |ω

(t) − ω

(τ| ≤ Cδ,

∀t ∈ [τ,τ + δ], ∀τ ∈ [0,T ],

(2)

|ω

(τ) − ω

(τ)| ≤ C

, ∀ τ ∈ [0, T ], (3)

(t) ≥ R, ∀t ∈ [0,T ] (4)

are satisﬁed. Here we assume that the quantity δ is

sufﬁciently small with respect to the ﬁxed numbers

T,C,C

, the number R is sufﬁciently great with re-

spect to the number δ.

The latter means that on the small intervals [τ,τ +

δ] the functions γ(t) and ω

(t) are ”almost constants”

and the functions f

(t) rapidly oscillate as harmonic

functions. It is clear that such conditions occur for

high-frequency oscillations.

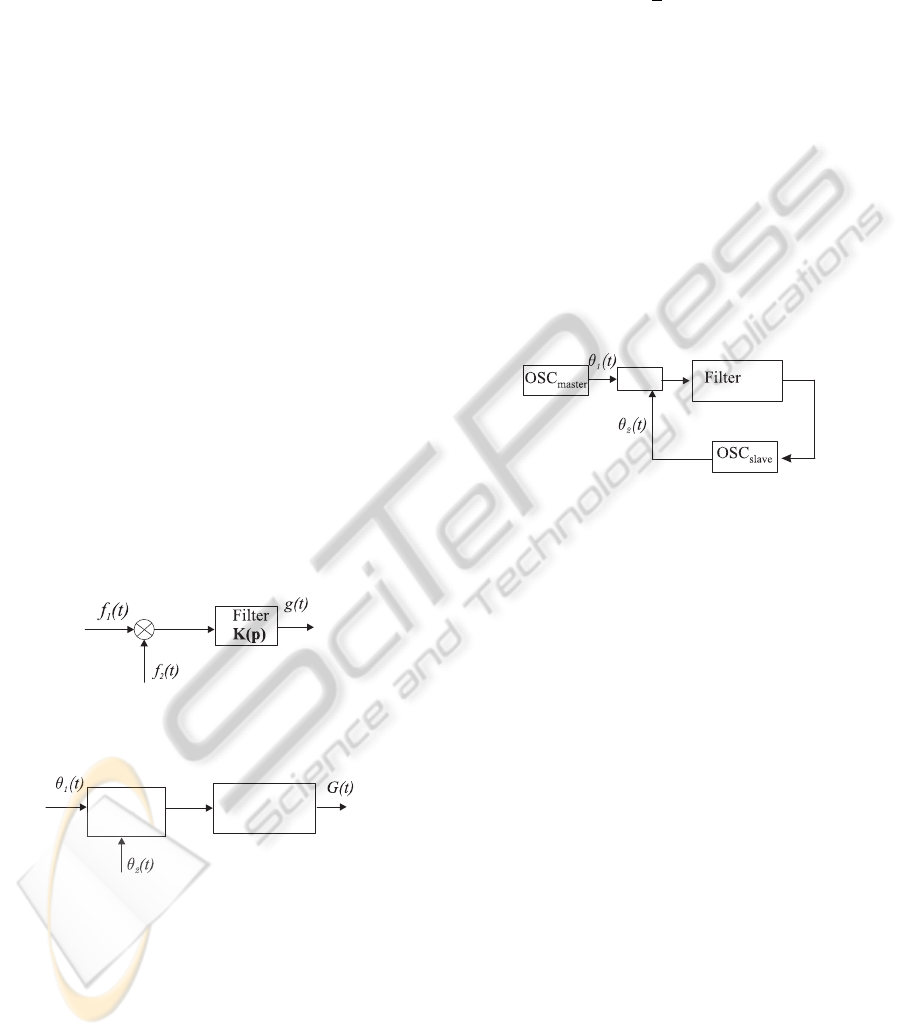
Consider two block diagram described in Fig. 2

and 3.

Figure 2: Multiplier and ﬁlter with transfer function K(p).

Filter

K(p)

Figure 3: Phase detector and ﬁlter.

Here θ

(t) = ω

(t)t + Ψ

are phases of the oscil-

lations f

(t), PD is a nonlinear block with the charac-

teristic ϕ(θ), being called a phase detector (discrimi-

nator). The phases θ

(t) enter the inputs of PD block

and the output is the function ϕ(θ

(t) − θ

(t)).

The signals f

(t) f

(t) and ϕ(θ

(t) − θ

(t)) enter

the same ﬁlters with the same impulse transient func-

tion γ(t). The ﬁlter outputs are the functions g(t) and

G(t) respectively.

A classical PLL synthesis is based on the follow-

ing result

Theorem 1. If conditions (2)–(4) are satisﬁed and

ϕ(θ) =

cosθ,

then for the same initial data of ﬁlter the following

relation

|G(t) − g(t)| ≤ C

δ, ∀t ∈ [0,T ].

is valid. Here C

is a certain number not depending

on δ.

Thus, the outputs of two block-diagrams in Fig. 2

and Fig. 3: g(t) and G(t), differ little from each other

and we can pass (from a standpoint of the asymptotic

with respect to δ) to the following description level,

namely to the level of phase relations 2).

In this case a block diagram in Fig. 1 passes to the

following block diagram (Fig. 4)

Figure 4: Block diagram of PLL on the level of phase rela-

tions.

Consider now the high-frequency oscillators, con-

nected by a diagram in Fig. 1. Here

(t) = A

sign sin(ω

(t)t + ψ

). (5)

We assume, as before, that conditions (2)–(4) are sat-

isﬁed.

Consider a 2π-periodic function ϕ(θ) of the form

ϕ(θ) =

(1 + 2θ/π) for θ ∈ [−π, 0],

(1 − 2θ/π) for θ ∈ [0, π].

(6)

and block-diagrams in Fig. 2 and 3.

Theorem 2. If conditions (2)–(4) are satisﬁed and

the characteristic of phase detector ϕ(θ) has the form

(6), then for the same initial data of ﬁlter the following

relation holds

|G(t) − g(t)| ≤ C

δ, ∀t ∈ [0,T ].

Here C

is a certain number not depending on δ.

Theorem 2 is a base for the synthesis of PLL with

impulse oscillators. It permits us for the impulse

clock oscillators to consider two block-diagrams in

parallel: on the level of electronic realization (Fig. 1)

and on the level of phase relations (Fig. 4), where the

common principles of the phase synchronization the-

ory can be applied. Thus, we can construct the theory

PHASE LOCKED LOOPS DESIGN AND ANALYSIS

115

of phase synchronization for the distributed system of

clocks in multiprocessor cluster.

Let us make a remark necessary to derive the dif-

ferential equations of PLL.

Consider a quantity

(t) = ω

(t) +

(t)t.

For the well-synthesized PLL, namely possessing

the property of global stability, we have an exponen-

tial damping of the quantity

(t):

(t)| ≤ Ce

−αt

Here C and α are certain positive numbers not de-

pending on t. Therefore the quantity

(t)t is, as a

rule, sufﬁciently small with respect to the number R

(see condition (2)– (4)).

From the above we can conclude that the follow-

ing approximate relation

(t) = ω

(t) (7)

is valid. When derived the differential equations of

this PLL, we make use of a block diagram in Fig. 4

and relation (7),which is assumed to be valid precisely

Note that, by assumption, the control low of tun-

able oscillators is linear:

(t) = ω

(0) + LG(t). (8)

Here ω

(0) is the initial frequency of tunable os-

cillator, L is a certain number, G(t) is a control signal,

which is a ﬁlter output (Fig. 4).

Thus, the equation of PLL is as follows

(t) = ω

(0)+L(α

(t)+

γ(t −τ). ϕ(θ

(τ)−θ

(τ))dτ).

Assuming that the master oscillator such that ω

(t) ≡

(0), we obtain the following relations for PLL

(θ

(t) − θ

(t))

•

+ L(α

(t) +

γ(t − τ).

ϕ(θ

(τ) − θ

(τ))dτ) = ω

(0) − ω

(0).

(9)

This is an equation of PLL.

Applying the similar approach, we can conclude

that in PLL the ﬁlters with transfer functions of more

general form can be used:

K(p) = a +W (p),

where a is a certain number, W (p) is a proper frac-

tional rational function. In this case in place of equa-

tion (9) we have

(θ

(t) − θ

(t))

•

+ L(a(ϕ(θ

(t) − θ

(t))+

+ α

(t) +

γ(t − τ)ϕ(θ

(τ) − θ

(τ))dτ) =

= ω

(0) − ω

(0).

(10)

In the case when the transfer function of the ﬁlter

a+W (p) is non degenerate, i.e. its numerator and de-

nominator do not have common roots, equation (10)

is equivalent to the following system of differential

equations

˙z = Az + bψ(σ)

σ = c

∗

z + ρψ(σ).

(11)

Here A is a constant n ×n-matrix, b and c are constant

n × n-vectors, ρ is a number, ψ(σ) is a 2π-periodic

function, satisfying the relations ρ = −aL

W (p) = L

−1

∗

(A − pI)

−1

ψ(σ) = ϕ(σ) −

(0) − ω

(0)

L(a +W (0))

Note that in (11) σ = θ

− θ

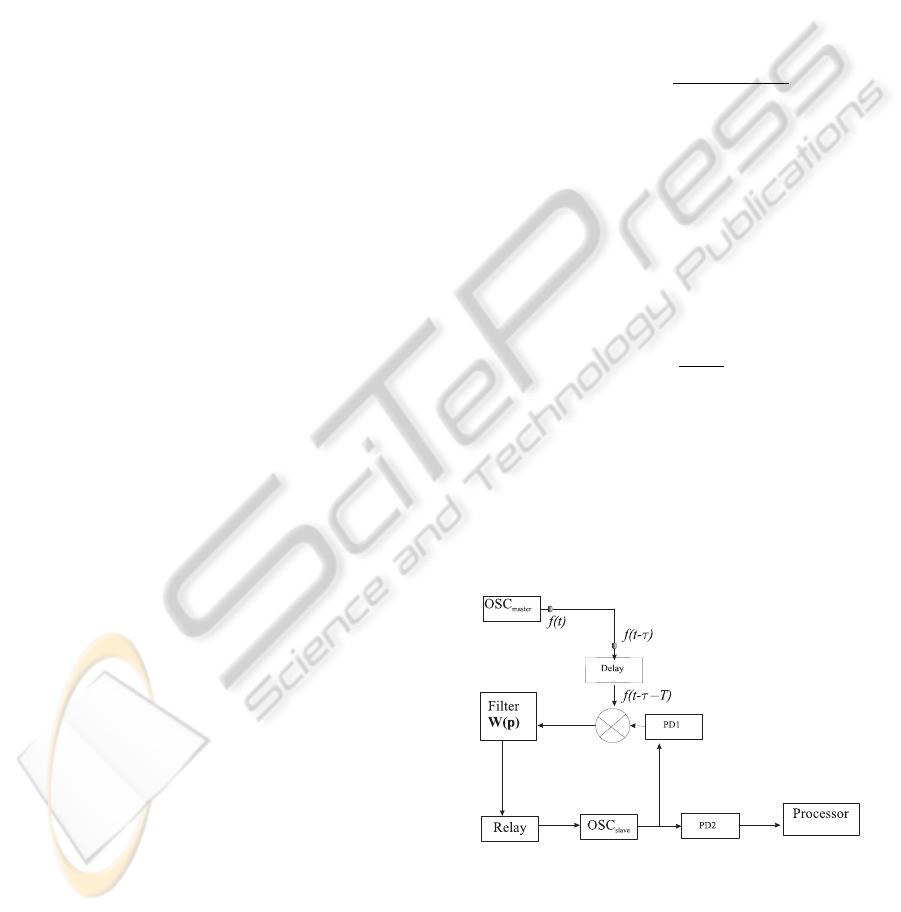
Using Theorem 2, we can make the design of a

block diagram of ﬂoating PLL, which plays a role of

the function of frequency synthesizer and the function

of correction of the clock-skew (see parameter τ in

Fig. 5).

Such a block diagram is shown in Fig. 5.

Here OSC

master

is a master oscillator, Delay is

a time-delay element, Filter is a ﬁlter with transfer

function

W (p) =

p + α

OSC

slave

is a slave oscillator, PD1 and PD2 are pro-

grammable dividers of frequencies, Processor is a

processor.

The Relay element plays a role of ﬂoating correct-

ing block. The introduction of it allow us to null a

residual clock skew, which arises for the nonzero ini-

tial difference of frequencies of master and slave os-

cillators.

Figure 5: Block diagram of PLL.

Note, the electronic realization of clock and delay

can be found in (Ugrumov, 2000; Razavi, 2003) and

that of multipliers, ﬁlters, and relays in (Aleksenko,

2004; Razavi, 2003). The description of dividers of

frequency can be found in (Solonina et al., 2000).

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

116

Assume, as usual, that the frequency of master os-

cillator is constant, namely ω

(t) ≡ ω

= const. The

parameter of delay line T is chosen in such a way that

(T + τ) = 2πk + 3π/2. Here k is a certain natural

number, ω

τ is a clock skew.

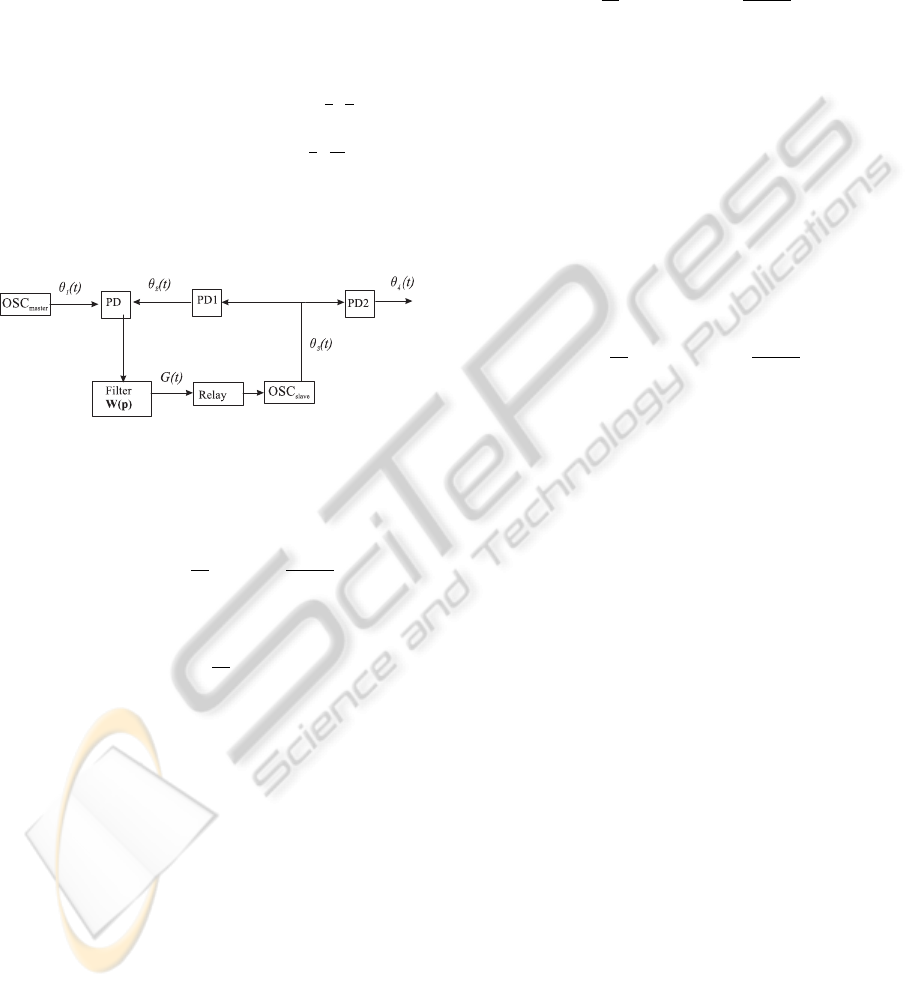
By Theorem 2 and the choice of T the block dia-

gram, shown in Fig. 6, can be changed by the close

block diagram, shown in Fig. 6.

Here 2π is a periodic characteristic of phase de-

tector. It has the form

ϕ(θ) =







θ/π forθ ∈ [−

]

(1 − θ/π) forθ ∈ [

3π

(12)

(t) = θ

(t)/M, θ

(t) = θ

(t)/N, where the nat-

ural numbers M and N are the parameters of pro-

grammable divisions PD1 and PD2.

Figure 6: Equivalent block diagram of PLL.

For transient process (capture mode) the following

conditions

lim

t→+∞

(θ

(t) −

(t)) =

2πkM

(13)

(phase capture)

lim

t→+∞

(

(t) −

(t)) = 0 (14)

(frequency capture) must be satisﬁed.

Relations (13) and (14) are the main requirements

of PLL for array processors. The time of transient

processors depends on the initial data and is sufﬁ-

ciently large for multiprocessors system (Leonov and

Seledzhi, 2002; Kung, 1988). Here a difference be-

tween the beginning of transient process and the be-

ginning of performance of parallel algorithm can be

some minutes. This difference is very large for the

electronic systems.

Assuming that the characteristic of relay is of the

form Ψ(G) = signG and the actuating element of

slave oscillator is linear, we have

(t) = RsignG(t) + ω

(0), (15)

where R is a certain number, ω

(0) is the initial fre-

quency, θ

(t) is a phase of slave oscillator.

Taking into account relations (15), (1), (12), and

the block diagram in Fig. 6, we have the following

differential equations of PLL

G + αG = βϕ(θ)

θ = −

signG + (ω

−

(0)

(16)

Here θ(t) = θ

(t) − θ

(t).

3 CRITERION OF GLOBAL

STABILITY OF PLL

System (16) can be written as

G = −αG + βϕ(θ)

θ = −F(G),

(17)

where

F(G) =

signG − (ω

−

(0)

Theorem 3. If the inequality

|R| > |Mω

− ω

(0)| (18)

is valid, then any solution of system (17) as t → +∞

tends to a certain equilibrium.

If the inequality

|R| < |Mω

− ω

(0)| (19)

is valid, then all the solutions of system (17) tends to

inﬁnity as t → +∞.

Consider the equilibria for system (17). For any

equilibrium we have

θ(t) ≡ 0, G(t) ≡ 0, θ(t) ≡ πk.

Theorem 4. Let relation (18) be valid. In this case,

if R > 0, then the following equilibria

G(t) ≡ 0, θ(t) ≡ 2kπ (20)

are locally asymptotically stable and the following

equilibria

G(t) ≡ 0, θ(t) ≡ (2k +1)π (21)

are locally unstable. If R < 0, then equilibria (21) are

locally asymptotically stable and equilibria (20) are

locally unstable.

Thus, for relations (13) and (14) to be satisﬁed it is

necessary to choice the parameters of system in such

a way that the inequality holds

R > |Mω

− ω

(0)|. (22)

PHASE LOCKED LOOPS DESIGN AND ANALYSIS

117

OSC

master

Filter

OSC

slave

Figure 7: Costas loop.

4 COSTAS LOOP

Consider now a block diagram of the Costas loop

(Fig. 7)

Here all denotations are the same as in Fig. 1, 90

– is a quadrature component. As before, we consider

here the case of the high-frequency harmonic and im-

pulse signals f

(t).

However together with the assumption that condi-

tions (2) and (4) are valid we assume also that (3) is

satisﬁed for the signal of the type (1) and the relation

|ω

(τ) − 2ω

(τ)| ≤ C

, ∀τ ∈ [0,T ], (23)

is valid for the signal of the type (5).

Applying the similar approach we can obtain dif-

ferential equation for the Costas loop, where

˙z = Az + bΨ(σ)

σ = c

∗

z + ρΨ(σ).

(24)

Here A is a constant n ×n-matrix, b and c are con-

stant n-vectors, ρ is a number, Ψ(σ) is a 2π-periodic

function, satisfying the following relations

ρ = −2aL, W (p) = (2L)

−1

∗

(A − pI)

−1

ψ(σ) =

sinσ −

(0) − ω

(0)

L(a +W (0))

σ = 2θ

− 2θ

(in the case (1);

ψ(σ) = P(σ) −

(0) − 2ω

(0)

2L(a +W (0))

P(σ) =











−

2σ

∈

[

]

− 2A

1 −

2σ

, σ ∈ [−π, 0]

σ = θ

− 2θ

(in the case (5).

From the above equations it follows that for

deterministic (when the noise is lacking) description

of the Costas loops the conventional introduction

of additional ﬁlters turns out unnecessary. Here a

central ﬁlter plays their role.

REFERENCES

Abramovitch, D., 2002. Phase-Locked Loope A control

Centric. Tutorial, in the Proceedings of the 2002 ACC.

Aleksenko, A., 2004. Digital engineering, Unimedstyle.

Moscow. (in Russian)

Best Ronald E., 2003. Phase-Lock Loops: Design, Simula-

tion and Application, McGraw Hill, 5

Egan, W.F., 2000. Frequency Synthesis by Phase Lock ,(2nd

ed.), John Wiley and Sons, 2

Gardner F., 2005. Phase–lock techniques, John Wiley &

Sons, New York, 2

Kroupa, V., 2003. Phase Lock Loops and Frequency Syn-

thesis, John Wiley & Sons.

Kung, S., 1988. VLSI Array Processors, Prentice Hall. New

York.

Lapsley, P., Bier, J., Shoham, A., Lee, E., 1997. DSP Pro-

cessor Fundamentals Architecture and Features, IEE

Press. New York.

Leonov, G., Reitmann, V., Smirnova, V., 1992. Nonlocal

Methods for Pendulum-Like Feedback Systems, Teub-

ner Verlagsgesselschaft. Stuttgart; Leipzig.

Leonov, G., Ponomarenko, D., Smirnova, V., 1996.

Frequency-Domain Methods for Nonlinear Analysis.

Theory and Applications, World Scientiﬁc. Singapore.

Leonov, G., Seledzhi, S., 2002. Phase locked loops in array

processors, Nevsky dialekt. St.Petersburg. (in Rus-

sian)

Lindsey, W., 1972, Sinchronization systems in communica-

tion and ontrol, Prentice-Hall. New Jersey.

Lindsey, W., Chie, C., 1981. A Survey of Digital Phase

Locked Loops. Proceedings of the IEEE.

Razavi, B., 2003. Phase-Locking in High-Performance Sys-

tems: From Devices to Architectures, John Wiley &

Sons.

Smith, S., 1999. The Scientist and Engineers Guide to Dig-

ital Dignal Processing, California Technical Publish-

ing. San Diego.

Solonina, A., Ulahovich, D., Jakovlev, L., 2000. The Mo-

torola Digital Signal Processors. BHV, St. Petersburg.

(in Russian)

Ugrumov, E., 2000. Digital engineering, BHV,

St.Petersburg. (in Russian)

Viterbi, A., 1966. Principles of coherent communications,

McGraw-Hill. New York.

ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics

118