
OPTIMAL CONTROL WITH ADAPTIVE INTERNAL
DYNAMICS MODELS
Djordje Mitrovic, Stefan Klanke and Sethu Vijayakumar
Institute of Perception, Action and Behavior, School of Informatics, University of Edinburgh, Edinburgh, U.K.
Keywords:
Learning dynamics, optimal control, adaptive control, robot simulation.
Abstract:
Optimal feedback control has been proposed as an attractive movement generation strategy in goal reaching
tasks for anthropomorphic manipulator systems. The optimal feedback control law for systems with non-linear
dynamics and non-quadratic costs can be found by iterative methods, such as the iterative Linear Quadratic
Gaussian (iLQG) algorithm. So far this framework relied on an analytic form of the system dynamics, which
may often be unknown, difficult to estimate for more realistic control systems or may be subject to frequent
systematic changes. In this paper, we present a novel combination of learning a forward dynamics model
within the iLQG framework. Utilising such adaptive internal models can compensate for complex dynamic
perturbations of the controlled system in an online fashion. The specific adaptive framework introduced lends
itself to a computationally more efficient implementation of the iLQG optimisation without sacrificing control
accuracy – allowing the method to scale to large DoF systems.
1 INTRODUCTION
We address the problem related to control of move-
ment in large degree of freedom (DoF) anthropomor-
phic manipulators, with specific emphasis on (target)
reaching tasks. This is challenging mainly due to
the large redundancies that such systems exhibit. For
example, a controller has to make a choice between
many different possible trajectories (kinematics) and
a multitude of applicable motor commands (dynam-
ics) for achieving a particular task. How do we re-
solve this redundancy?
Optimal control theory (Stengel, 1994) answers
this question by postulating that a particular choice
is made because it is the optimal solution to the task.
Most optimal motor control models so far have fo-
cused on open loop optimisation in which the se-
quence of motor commands or the trajectory is di-
rectly optimised with respect to some cost function,
for example, minimum jerk (Flash and Hogan, 1985),
minimum torque change (Uno et al., 1989), minimum
end point variance (Harris and Wolpert, 1998), etc.
Trajectory planning and execution steps are separated
and errors during execution are compensated for by
using a feedback component (e.g., PID controller).
However, these corrections are not taken into account
in the optimisation process.
A suggested alternative to open loop models are
closed loop optimisation models, namely optimal
feedback controllers (OFC) (Todorov, 2004). In con-
trast to open loop optimisation that just produces a de-
sired optimal trajectory, in OFC, the gains of a feed-
back controller are optimised to produce an optimal
mapping from state to control signals (control law). A
key property of OFC is that errors are only corrected
by the controller if they adversely affect the task per-
formance, otherwise they are neglected (minimum
intervention principle (Todorov and Jordan, 2003)).
This is an important property especially in systems
that suffer from control dependent noise, since task-
irrelevant correction could destabilise the system be-
side expending additional control effort. Another in-
teresting feature of OFC is that desired trajectories
do not need to be planned explicitly but they sim-
ply fall out from the feedback control laws. Empir-
ically, OFC also accounts for many motion patterns
that have been observed in natural, redundant systems
and human experiments (Shadmehr and Wise, 2005)
141
Mitrovic D., Klanke S. and Vijayakumar S. (2008).
OPTIMAL CONTROL WITH ADAPTIVE INTERNAL DYNAMICS MODELS.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - ICSO, pages 141-148
DOI: 10.5220/0001484501410148
Copyright
c
SciTePress

including the confounding trial-to-trial variability in
individual degrees of freedom that, remarkably, man-
ages to not compromise task optimality (Li, 2006;
Scott, 2004). Therefore, this paradigm is potentially a
very attractive control strategy for artificial anthropo-
morphic systems (i.e., large DoF, redundant actuation,
flexible lightweight construction, variable stiffness).
Finding an optimal control policy for nonlinear
systems is a big challenge because they do not fol-
low the well explained Linear-Quadratic-Gaussian
formalism (Stengel, 1994). Global solutions could
be found in theory by applying dynamic program-
ming methods (Bertsekas, 1995) that are based on
the Hamilton-Jacobi-Bellman equations. However, in
their basic form these methods rely on a discretisa-
tion of the state and action space, an approach that is
not viable for large DoF systems. Some research has
been carried out on random sampling in a continuous
state and action space (Thrun, 2000), and it has been
suggested that sampling can avoid the curse of dimen-
sionality if the underlying problem is simple enough
(Atkeson, 2007), as is the case if the dynamics and
cost functions are very smooth.
As an alternative, one may use iterative ap-
proaches that are based on local approximations of
the cost and dynamics functions, such as differen-
tial dynamic programming (Jacobson and Mayne,
1970), iterative linear-quadratic regulator designs (Li
and Todorov, 2004), or the recent iterative Linear
Quadratic Gaussian (iLQG) framework (Todorov and
Li, 2005; Li and Todorov, 2007), which will form the
basis of our work.
A major shortcoming of iLQG is its dependence
on an analytic form of the system dynamics, which
often may be unknown or subject to change. We over-
come this limitation by learning an adaptive internal
model of the system dynamics using an online, su-
pervised learning method. We consequently use the
learned models to derive an iLQG formulation that is
computationally less expensive (especially for large
DoF systems), reacts optimally to transient perturba-
tions as well as adapts to systematic changes in plant
dynamics.
The idea of learning the system dynamics in com-
bination with iterative optimisations of trajectory or
policy has been explored previously in the literature,
e.g., for learning to swing up a pendulum (Atkeson
and Schaal, 1997) using some prior knowledge about
the form of the dynamics. Similarly, Abeel et al.
(Abbeel et al., 2006) proposed a hybrid reinforcement
learning algorithm, where a policy and an internal
model get subsequently updated from “real life” tri-
als. In contrast to their method, however,we (or rather
iLQG) employ second-order optimisation methods,
and we iteratively refine the control policy solely from
the internal model. To our knowledge, learning dy-
namics in conjunction with control optimisation has
not been studied in the light of adaptability to chang-
ing plant dynamics.
The remainder of this paper is organised as fol-
lows: In the next section, we recall some basic con-
cepts of optimal control theory and we briefly de-
scribe the iLQG framework. In Section 3, we intro-
duce our extension to that framework, and we explain
how we include a learned internal model of the dy-
namics. We demonstrate the benefits of our method
experimentally in Section 4, and we conclude the pa-
per with a discussion of our work and future research
directions in Section 5.
2 LOCALLY-OPTIMAL
FEEDBACK CONTROL
Let x(t) denote the state of a plant and u(t) the applied
control signal at time t. In this paper, the state con-
sists of the joint angles q and velocities
˙
q of a robot,
and the control signals u are torques. If the system
would be deterministic, we could express its dynam-
ics as ˙x = f(x,u), whereas in the presence of noise we
write the dynamics as a stochastic differential equa-
tion
dx = f(x, u)dt + F(x,u)dω
ω
ω. (1)
Here, dω
ω
ω is assumed to be Brownian motion noise,
which is transformed by a possibly state- and control-
dependent matrix F(x,u). We state our problem as
follows: Given an initial state x
0
at time t = 0, we
seek a control sequence u(t) such that the system’s
state is x
∗
at time t = T. Stochastic optimal control
theory approaches the problem by first specifying a
cost function which is composed of (i) some evalua-
tion h(x(T)) of the final state, usually penalising de-
viations from the desired state x
∗
, and (ii) the accu-
mulated cost c(t,x,u) of sending a control signal u
at time t in state x, typically penalising large motor
commands. Introducing a policy π
π
π(t,x) for selecting
u(t), we can write the expected cost of following that
policy from time t as (Todorov and Li, 2005)
v
π
π
π
(t,x(t)) =
D
h(x(T)) +
Z
T
t
c(s,x(s),π
π
π(s,x(s)))ds
E
(2)
One then aims to find the policy π
π
π that minimises
the total expected cost v
π
π
π
(0,x
0
). Thus, in contrast to
classical control, calculation of the trajectory (plan-
ning) and the control signal (execution) is not sep-
arated anymore, and for example, redundancy can
actually be exploited in order to decrease the cost.
If the dynamics f is linear in x and u, the cost is
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
142

iLQG
u
plant
learned
dynamics model
+
feedback
controller
x, dx
L, x
u
u
perturbations
x
cost function
(incl. target)
δ
-
-
u +
-
u
δ
Figure 1: Illustration of our iLQG–LD learning and control scheme.
quadratic, and the noise is Gaussian, the resulting so-
called LQG problem is convex and can be solved an-
alytically (Stengel, 1994).
In the more realistic case of non-linear dynamics
and non-quadratic cost, one can make use of time-
varying linear approximations and apply a similar for-
malism to iteratively improve a policy, until at least
a local minimum of the cost function is found. The
resulting iLQG algorithm has only recently been in-
troduced (Todorov and Li, 2005), so we give a brief
summary in the following.
One starts with an initial time-discretised control
sequence
¯
u
k
≡
¯
u(k∆t) and applies the deterministic
forward dynamics to retrieve an initial trajectory
¯
x
k
,
where
¯
x
k+1
=
¯
x
k
+ ∆t f(
¯
x
k
,
¯
u
k
). (3)
Linearising the discretised dynamics (1) around
¯
x
k
and
¯
u
k
and subtracting (3), one gets a dynamics equa-
tion for the deviations δx
k
= x
k
−
¯
x
k
and δu
k
= u
k
−
¯
u
k
:
δx
k+1
=
I+ ∆t
∂f
∂x
¯
x
k
δx
k
+ ∆t
∂f
∂u
¯
u
k
δu
k
+
√
∆t
F(u
k
) +
∂F
∂u
¯
u
k
δu
k
ξ
ξ
ξ
k
. (4)
Here, ξ
ξ
ξ
k
represents zero mean Gaussian noise. Sim-
ilarly, one can derive an approximate cost function
which is quadratic in δu and δx. Thus, in the vicin-
ity of the current trajectory
¯
x, the two approxima-
tions form a “local” LQG problem, which can be
solved analytically and yields an affine control law
δu
k
= l
k
+ L
k
δx
k
(for details please see (Todorov and
Li, 2005)). This control law is fed into the linearised
dynamics (eq. 4 without the noise term) and the re-
sulting δx are used to update the trajectory
¯
x. In the
same way, the control sequence
¯
u is updated from δu.
This process is repeated until the total cost cannot be
reduced anymore. The resultant control sequence
¯
u
can than be applied to the system, whereas the matri-
ces L
k
from the final iteration may serve as feedback
gains.
In our current implementation
1
, we do not utilise
an explicit noise model F for the sake of clarity of
results; in any case, a matching feedback control law
1
We used an adapted version of the iLQG implementa-
tion at: www.cogsci.ucsd.edu/∼todorov/software.htm
is only marginally superior to one that is optimised
for a deterministic system (Todorov and Li, 2005).
3 iLQG WITH LEARNED
DYNAMICS (iLQG–LD)
In order to eliminate the need for an analytic dynam-
ics model and to make iLQG adaptive, we wish to
learn an approximation
˜
f of the real plant forward dy-
namics
˙
x = f(x,u). Assuming our model
˜
f has been
coarsely pre-trained, for example by motor babbling,
we can refine that model in an online fashion as shown
in Fig. 1. For optimising and carrying out a move-
ment, we have to define a cost function (where also
the desired final state is encoded), the start state, and
the number of discrete time steps. Given an initial
torque sequence
¯
u
0
, the iLQG iterations can be car-
ried out as described in the previous section, but utilis-
ing the learned model
˜
f. This yields a locally optimal
control sequence
¯
u
k
, a corresponding desired state se-
quence
¯
x
k
, and feedback correction gain matrices L
k
.
Denoting the plant’s true state by x, at each time step
k, the feedback controller calculates the required cor-
rection to the control signal as δu
k
= L
k
(x
k
−
¯
x
k
). We
then use the final control signal u
k
=
¯
u
k
+ δu
k
, the
plant’s state x
k
and its change dx
k
to update our inter-
nal forward model
˜
f. As we show in Section 4, we can
thus account for (systematic) perturbations and also
bootstrap a dynamics model from scratch.
The domain of real-time robot control demands
certain properties of a learning algorithm, namely fast
learning rates, high prediction speeds at run-time, and
robustness towards negative interference if the model
is trained incrementally. Locally Weighted Projec-
tion Regression (LWPR) has been shown to exhibit
these properties, and to be very efficient for incremen-
tal learning of non-linear models in high dimensions
(Vijayakumar et al., 2005). In LWPR, the regression
function is constructed by blending local linear mod-
els, each of which is endowed with a locality kernel
that defines the area of its validity (also termed its re-
ceptive field). During training, the parameters of the
local models (locality and fit) are updated using in-
cremental Partial Least Squares, and models can be
pruned or added on an as-need basis, for example,
OPTIMAL CONTROL WITH ADAPTIVE INTERNAL DYNAMICS MODELS
143

when training data is generated in previously unex-
plored regions.
Usually the receptive fields of LWPR are mod-
elled by Gaussian kernels, so their activation or re-
sponse to a query vector z (combined inputs x and u
of the forward dynamics
˜
f) is given by
w
k
(z) = exp
−
1
2
(z−c
k
)
T
D
k
(z−c
k
)
, (5)
where c
k
is the centre of the k
th
linear model and D
k
is its distance metric. Treating each output dimension
separately for notational convenience, the regression
function can be written as
˜
f(z) =
1
W
K
∑
k=1
w
k
(z)ψ
k
(z), W =
K
∑
k=1
w
k
(z), (6)
ψ
k
(z) = b
0
k
+ b
T
k
(z−c
k
), (7)
where b
0
k
and b
k
denote the offset and slope of the k-th
model, respectively.
LWPR learning has the desirable property that it
can be carried out online, and moreover, the learned
model can be adapted to changes in the dynamics in
real-time. A forgetting factor λ (Vijayakumar et al.,
2005), which balances the trade-off between preserv-
ing what has been learned and quickly adapting to the
non-stationarity, can be tuned to the expected rate of
external changes. As we will see later, the factor λ
can be used to model biologically realistic adaptive
behaviour to external force-fields.
So far, we have shown how the problem of un-
known or changing system dynamics can be solved
within iLQG–LD. Another important issue to address
is the computational complexity. The iLQG frame-
work has been shown to be the most effective locally
optimal control method in terms of convergencespeed
and accuracy (Li, 2006). Nevertheless the computa-
tional cost of iLQG remains daunting even for sim-
ple movement systems, preventing their application
to real-time, large DoF systems. A major component
of the computational cost is due to the linearisation of
the system dynamics, which involves repetitive calcu-
lation of the system dynamics’ derivatives ∂f/∂x and
∂f/∂u. When the analytical form of these derivatives
is not available, they must be approximated using fi-
nite differences. The computational cost of such an
approximation scales linearly with the sum of the di-
mensionalities of x = (q;
˙
q) and u = τ
τ
τ (i.e., 3N for an
N DoF robot). In simulations, our analysis show that
for the 2 DoF manipulator, 60% of the total iLQG
computations can be attributed to finite differences
calculations. For a 6 DoF arm, this rises to 80%.
Within our iLQG–LD scheme, we can avoid finite dif-
ference calculations and rather use the analytic deriva-
tives of the learned model, as has also been proposed
in (Atkeson et al., 1997). Differentiating the LWPR
predictions (6) with respect to z = (x;u) yields terms
∂
˜
f(z)
∂z
=
1
W
∑
k
∂w
k
∂z
ψ
k
(z) + w
k
∂ψ
k
∂z
−
1
W
2
∑
k
w
k
(z)ψ
k
(z)
∑
l
∂w
l
∂z
(8)
=
1
W
∑
k
(−ψ
k
w
k
D
k
(z−c
k
) + w
k
b
k
)
+
˜
f(z)
W
∑
k
w
k
D
k
(z−c
k
) (9)
for the different rows of the Jacobian matrix
∂
˜
f/∂x
∂
˜
f/∂u
=
∂
∂z
(
˜
f
1
,
˜
f
2
,...
˜
f
N
)
T
.
Table 1 illustrates the computational gain (mean CPU
time per iLQG iteration) across 4 test manipulators
– highlighting added benefits for more complex sys-
tems. On a notebook running at 1.6 GHz, the average
CPU times for a complete iLQG trajectory using the
analytic method are 0.8 sec (2 DoF), 1.9 sec (6 DoF),
and 9.8 sec (12 DoF), respectively. Note that LWPR
is a highly parallelisable algorithm: Since the local
models learn independently of each other, the respec-
tive computations could be distributed across multi-
ple processors, which would yield a further significant
performance gain.
Table 1: CPU time for one iLQG–LD iteration (sec).
manipulator: 2 DoF 6 DoF 12 DoF
finite differences 0.438 4.511 29.726
analytic Jacobian 0.193 0.469 1.569
improvement factor 2.269 9.618 18.946
4 EXPERIMENTS
We studied iLQG–LD on two different joint torque
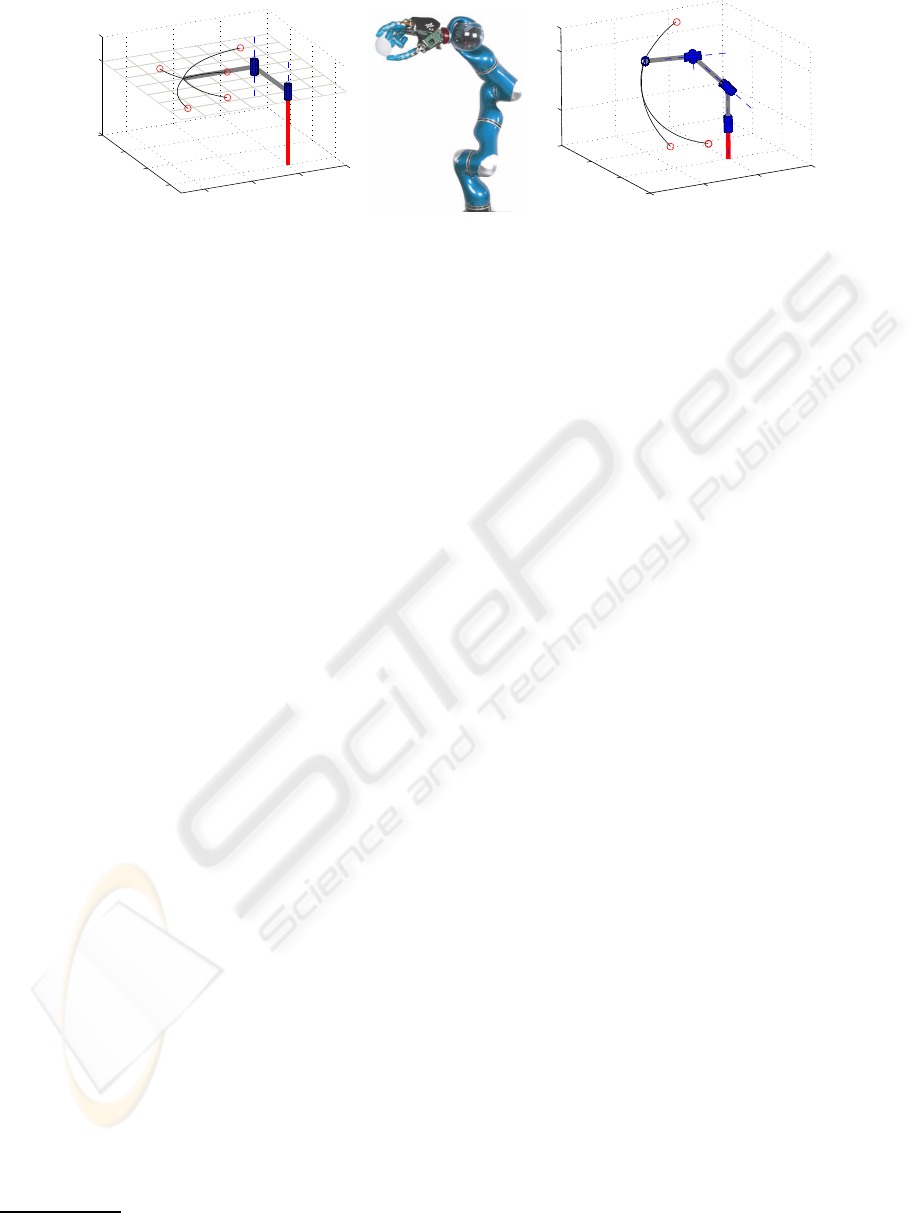
controlled manipulators. The first (Fig. 2, left) is a
horizontally planar 2 DoF manipulator similar to the
one used in (Todorov and Li, 2005). This low DoF
system is ideal for performing extensive (quantitative)
comparison studies and to test the manipulator under
controlled perturbations and force fields during planar
motion. The second experimental setup is a 6 DoF
manipulator, the physical parameters (i.e., inertia ten-
sors, mass, gear ratios etc.) of which are a faithful
model of the actual DLR Light-Weight Robot (LWR)
from the German Aerospace Centre
2
(Fig. 2, right).
2
http://www.dlr.de
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
144
−40
−20
0
20
0
20
40
60
0
X (cm)
Y (cm)
Z (cm)
-100
-50
0
50
-50
0
50
100
0
50
X (cm)
Y (cm)
Z (cm)
Figure 2: Two different manipulator models with selected targets (circles) and iLQG generated trajectories as benchmark data.
All models are simulated using the Matlab Robotics Toolbox. Left: 2 DoF planar manipulator model; Middle: picture of real
LWR; Right: 6 DoF LWR model (without hand).
This setup is used to evaluate iLQG–LD on a realis-
tic, redundant anthropomorphic system.
Our simulation model computes the non-linear
plant dynamics using standard equations of motion.
For an N-DoF manipulator the joint torques τ
τ
τ are
given by
τ
τ
τ = M(q)
¨
q+ C(q,
˙
q)
˙
q+ b(
˙
q) + g(q), (10)
where q and
˙
q are the joint angles and joint velocities
respectively; M(q) is the N-dimensional symmetric
joint space inertia matrix, C(q,
˙
q) accounts for Corio-
lis and centripetal effects, b(
˙
q) describes the viscous
and Coulomb friction in the joints, and g(q) defines
the gravity loading depending on the joint angles q of
the manipulator. It is important to note that while the
above analytical dynamics perfectly match the system
dynamics in simulation, they are at best, an extremely
crude approximation to the dynamics of the real hard-
ware arm.
We study movements for a fixed motion duration
of one second, which we discretise into K = 100 steps
(∆t = 0.01s). The manipulator starts at an initial po-
sition q
0
and reaches towards a target q
tar
. During
movement we wish to minimise the energy consump-
tion of the system. We therefore use the cost function
3
v = w
p
|q
K
−q
tar
|
2
+ w
v
|
˙
q
K
|
2
+ w
e
K
∑
k=0
|u
k
|
2
∆t,
(11)
where the factors for the target position accuracy
(w
p
), the final target velocity accuracy (w
v
), and for
the energy term (w
e
) weight the importance of each
component.
We compare the control results of iLQG–LD and
iLQG with respect to the number of iterations, the
end point accuracy and the generated costs. We first
present results for the 2 DoF planar arm in order
to test whether our theoretical assumptions hold and
iLQG–LD works in practice (Sections 4.1 and 4.2). In
3
We specify the target in joint space only for the 2-DoF
arm.
a final experiment, we present qualitative and quan-
titative results to show that iLQG–LD scales up to
the redundant 6 DoF anthropomorphic system (Sec-
tion 4.3).
4.1 Stationary Dynamics
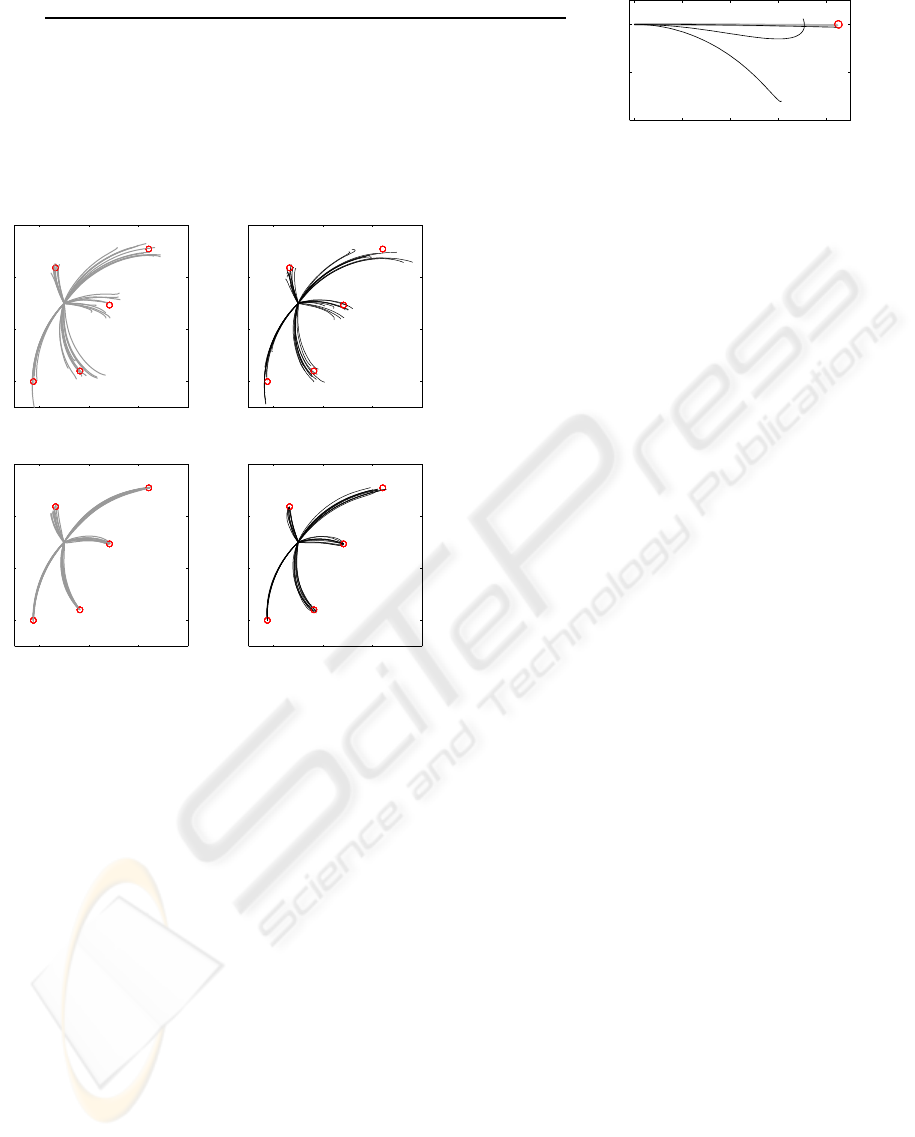
First, we compared the characteristics of iLQG–LD
and iLQG (both operated in open loop mode) in the
case of stationary dynamics without any noise in the
2 DoF plant. Fig. 3 shows three trajectories gener-
ated by learned models of different predictive quality
(reflected by the different test nMSE). As one would
expect, the quality of the model plays an important
role for the final cost, the number of iLQG–LD it-
erations, and the final target distances (cf. the table
within Fig. 3). For the final learned model, we ob-
serve a striking resemblance with the analytic iLQG
performance. Real world systems usually suffer
from control dependent noise, so in order to be prac-
ticable, iLQG–LD has to be able to cope with this.
Next, we carried out a reaching task to 5 reference tar-
gets covering a wide operating area of the planar arm.
To simulate control dependent noise, we contami-
nated commands u just before feeding them into the
plant, using Gaussian noise with 50% of the variance
of the signal u. We then generated motor commands
to move the system towards the targets, both with and
without the feedback controller. As expected, closed
loop control (utilising gain matrices L
k
) is superior to
open loop operation regarding reaching accuracy. Fig.
4 depicts the performanceof iLQG–LD and iLQG un-
der both control schemes. Averaged over all trials,
both methods show similar endpoint variancesand be-
haviour which is statistically indistinguishable.
OPTIMAL CONTROL WITH ADAPTIVE INTERNAL DYNAMICS MODELS
145
iLQG–LD (L) (M) (H) iLQG
Train. points 111 146 276 –
Prediction error (nMSE) 0.80 0.50 0.001 –
iterations 19 17 5 4
Cost 2777.36 1810.20 191.91 192.07
Eucl. target distance (cm) 19.50 7.20 0.40 0.01
0 10 20 30 40 cm
-20
-10
0
cm
(L)
(M)
(H)
Figure 3: Behaviour of iLQG–LD for learned models of different quality. Right: Trajectories in task space produced by
iLQG–LD (black lines) and iLQG (grey line).
−40 −20 0 cm
0
20
40
open loop iLQG
d = 2.71±1.84 cm
−40 −20 0 cm
0
20
40
open loop iLQG–LD
d = 3.20±1.60 cm
−40 −20 0 cm
0
20
40
closed loop iLQG
d = 0.19±0.001 cm
−40 −20 0 cm
0
20
40
closed loop iLQG–LD
d = 0.18±0.001 cm
Figure 4: Illustration of the target reaching performances
for the planar 2 DoF in the presence of strong control de-
pendent noise, where d represents the average Euclidean
distance to the five reference targets.
4.2 Non-stationary Dynamics
A major advantage of iLQG–LD is that it does not
rely on an accurate analytic dynamics model; conse-
quently, it can adapt ‘on-the-fly’ to external perturba-
tions and to changes in the plant dynamics that may
result from altered morphology or wear and tear.
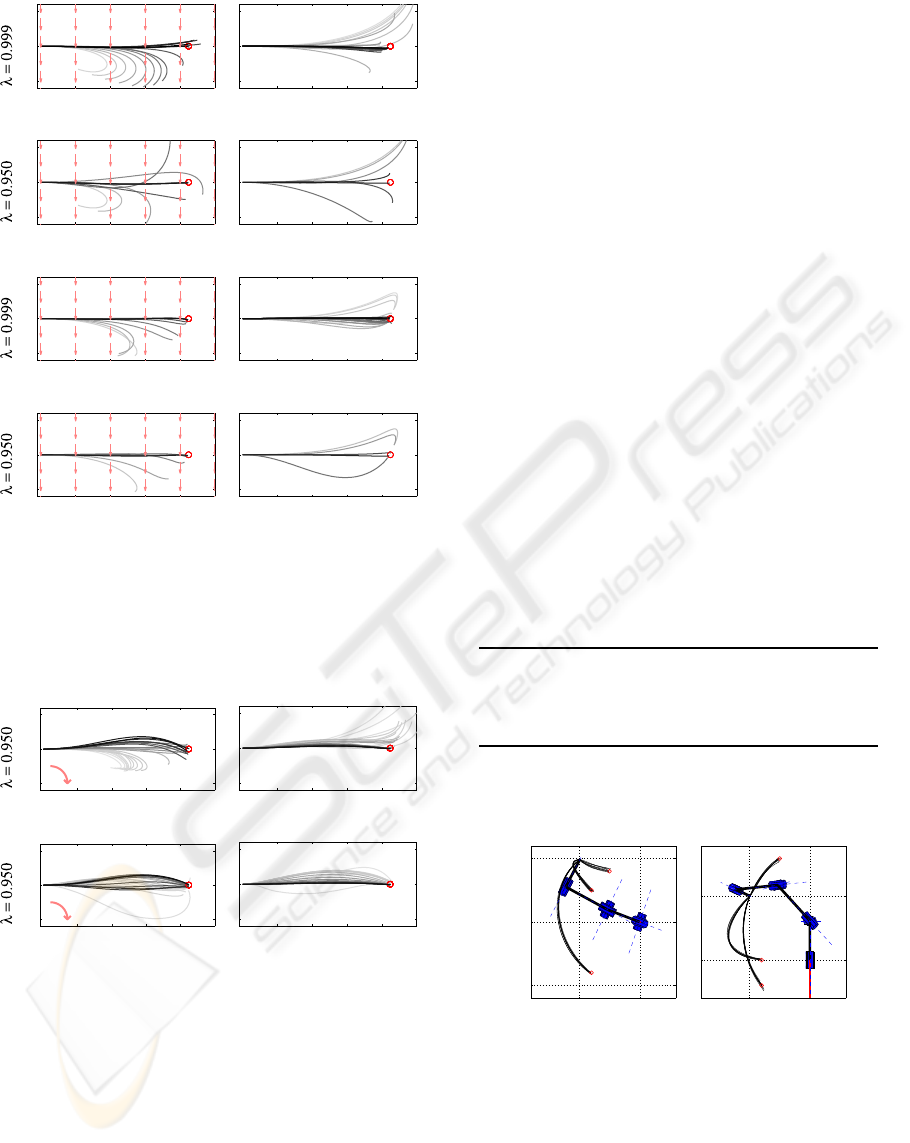
We carried out adaptive reaching experiments in
our simulation similar to the human manipulandum
experiments in (Shadmehr and Mussa-Ivaldi, 1994).
First, we generated a constant unidirectional force
field (FF) acting perpendicular to the reaching move-
ment (see Fig. 5). Using the iLQG–LD models
from the previous experiments, the manipulator gets
strongly deflected when reaching for the target be-
cause the learned dynamics model cannot account for
the “spurious” forces. However, using the resultant
deflected trajectory (100 data points) as training data,
updating the dynamics model online brings the ma-
nipulator nearer to the target with each new trial. We
repeated this procedure until the iLQG–LD perfor-
mance converged successfully. At that point, the in-
ternal model successfully accounts for the change in
dynamics caused by the FF. Then, removing the FF
results in the manipulator overshooting to the other
side, compensating for a non-existing FF. Just as be-
fore, we re-adapted the dynamics online over repeated
trials.
Fig. 5 summarises the results of the sequential
adaptation process just described. The closed loop
control scheme clearly converges faster than the open
loop scheme, which is mainly due to the OFC’s desir-
able property of always correcting the system towards
the target. Therefore, it produces relevant dynamics
training data in a way that could be termed “active
learning”. Furthermore, we can accelerate the adapta-
tion process significantly by tuning the forgetting fac-
tor λ, allowing the learner to weight the importance of
new data more strongly (Vijayakumar et al., 2005). A
value of λ = 0.95 produces significantly faster adapta-
tion results than the default of λ = 0.999. As a follow-
up experiment, we made the force field dependent on
the velocity v of the end-effector, i.e. we applied a
force
F = Bv, with B =
0 50
−50 0
Nm
−1
s (12)
to the end-effector. The results are illustrated in Fig.
6: For the more complex FF, more iterations are
needed in order to adapt the model, but otherwise
iLQG–LD shows a similar behaviour as for the con-
stant FF. Interestingly, the overshooting behaviour de-
picted in Fig. 5 and 6 has been observed in human
adaptation experiments (Shadmehr and Mussa-Ivaldi,
1994). We believe this to be an interesting insight for
future investigation of iLQG–LD and its role in mod-
eling sensorimotor adaptation data in the (now exten-
sive) human reach experimental paradigm (Shadmehr
and Wise, 2005).
4.3 iLQG–LD for 6 DoF
In the 6 DoF LWR, we studied reaching targets speci-
fied in task space coordinates r ∈ R
3
in order to high-
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
146
10 20 30 40 cm
−10
0
10
n = 1500
10 20 30 40 cm
−10
0
10
n = 3000
10 20 30 40 cm
−10
0
10
n = 900
10 20 30 40 cm
−10
0
10
n = 700
10 20 30 40 cm
−10
0
10
n = 1100
10 20 30 40 cm
−10
0
10
n = 2400
10 20 30 40 cm
−10
0
10
n = 500
10 20 30 40 cm
−10
0
10
n = 500
Figure 5: Illustration of adaptation experiments for open
loop (rows 1,2) and closed loop (rows 3,4) iLQG–LD. Ar-
rows depict the presence of a (constant) force field; n repre-
sents the number of training points required to successfully
update the internal LWPR dynamics model. Darker lines
indicate better trained models, corresponding to later trials
in the adaption process.
10 20 30 40
−0.1
0
0.1
n = 3500
10 20 30 40
−10
0
10
n = 3000
10 20 30 40
−0.1
0
0.1
n = 1400
10 20 30 40
−10
0
10
n = 1900
Figure 6: Adaptation to a velocity-dependent force field
(as indicated by the bent arrow) and re-adaptation after the
force field is switched off (right column). Top: open loop.
Bottom: closed loop.
light the redundancyresolution capability and trial-to-
trial variability in large DoF systems. Therefore, we
replaced the term |q
K
−q
tar
|
2
by |r(q
K
) −r
tar
|
2
in
(11), where r(q) denotes the forward kinematics.
Similar to the 2 DoF, we bootstrapped a forward dy-
namics model through ‘motor babbling’. Next, we
used iLQG–LD (closed loop, with noise) to train our
dynamics model online until it converged to stable
reaching behaviour. Fig. 7 (left) depicts reaching
trials, 20 for each reference target, using iLQG–LD
with the final learned model. Table 2 quantifies the
performance. The targets are reached reliably and no
statistically significant differences can be spotted be-
tween iLQG–LD and iLQG. An investigation of the
trials in joint angle space also shows similarities. Fig.
7 (right) depicts the 6 joint angle trajectories for the
20 reaching trials towards target (c). The joint angle
variances are much higher compare d to the variances
of the task space trajectories, meaning that task irrel-
evant errors are not corrected unless they adversely
affect the task (minimum intervention principle of
OFC). Moreover, the joint angle variances (trial-to-
trial variability) between the iLQG–LD and iLQG tri-
als are in a similar range, indicating an equivalent cor-
rective behaviour – the shift of the absolute variances
can be explained by the slight mismatch in between
the learned and analytical dynamics. We can conclude
from our results that iLQG–LD scales up very well to
6 DoF, not suffering from any losses in terms of accu-
racy, cost or convergence behaviour. Furthermore, its
computational cost is significantly lower than the one
of iLQG.
Table 2: Comparison of iLQG–LD and iLQG for control-
ling a 6 DOF arm to reach for three targets.
iLQG–LD Iter. Run. cost d (cm)
(a) 17 18.32 ±0.55 1.92 ±1.03
(b) 30 18.65 ±1.61 0.53 ±0.20
(c) 51 12.18 ±0.03 2.00 ±1.02
iLQG Iter. Run. cost d (cm)
(a) 19 18.50 ±0.13 2.63 ±1.63
(b) 26 18.77 ±0.25 1.32 ±0.69
(c) 48 12.92 ±0.04 1.75 ±1.30
cm
cm−50
0
−50
0
50
X
Y
(a)
(b)
(c)
cm
cm
−50 0
0
50
X
Z
(b)
(a)
(c)
Figure 7: Illustration of the 6-DoF manipulator and the tra-
jectories for reaching towards the targets (a,b,c). Left: top-
view, right: side-view.
5 CONCLUSIONS
In this work we introduced iLQG–LD, a method that
realises adaptive optimal feedback control by incor-
porating a learned dynamics model into the iLQG
OPTIMAL CONTROL WITH ADAPTIVE INTERNAL DYNAMICS MODELS
147

(1)
(2)
(3)
iLQG
iLQG-LD
(4)
(5)
(6)
Figure 8: Illustration of the trial-to-trial variability of the 6-
DoF arm when reaching towards target (c). The plots depict
the joint angles (1–6) over time. Grey lines indicate iLQG,
black lines stem from iLQG–LD.
framework. Most importantly, we carried over the
favourable properties of iLQG to more realistic con-
trol problems where the analytic dynamics model is
often unknown, difficultto estimate accurately or sub-
ject to changes.
Utilising the derivatives (8) of the learned dynam-
ics model
˜
f avoids expensive finite difference cal-
culations during the dynamics linearisation step of
iLQG. This significantly reduces the computational
complexity, allowing the framework to scale to larger
DoF systems. We empirically showed that iLQG–LD
performs reliably in the presence of noise and that it
is adaptive with respect to systematic changes in the
dynamics; hence, the framework has the potential to
provide a unifying tool for modelling (and informing)
non-linear sensorimotor adaptation experiments even
under complex dynamic perturbations. As with iLQG
control, redundancies are implicitly resolved by the
OFC framework through a cost function, eliminating
the need for a separate trajectory planner and inverse
kinematics/dynamics computation.
Our future work will concentrate on implement-
ing the iLQG–LD frameworkon the anthropomorphic
LWR hardware – this will not only explore an alterna-
tive control paradigm, but will also provide the only
viable and principled control strategy for the biomor-
phic variable stiffness based highly redundant actua-
tion system that we are currently developing. Indeed,
exploiting this framework for understanding OFC and
its link to biological motor control is another very im-
portant strand.
REFERENCES
Abbeel, P., Quigley, M., and Ng, A. Y. (2006). Using inac-
curate models in reinforcement learning. In Proc. Int.
Conf. on Machine Learning, pages 1–8.
Atkeson, C. G. (2007). Randomly sampling actions in
dynamic programming. In Proc. Int. Symp. on Ap-
proximate Dynamic Programming and Reinforcement
Learning, pages 185–192.
Atkeson, C. G., Moore, A., and Schaal, S. (1997). Locally
weighted learning for control. AI Review, 11:75–113.
Atkeson, C. G. and Schaal, S. (1997). Learning tasks from a
single demonstration. In Proc. Int. Conf. on Robotics
and Automation (ICRA), volume 2, pages 1706–1712,
Albuquerque, New Mexico.
Bertsekas, D. P. (1995). Dynamic programming and optimal
control. Athena Scientific, Belmont, Mass.
Flash, T. and Hogan, N. (1985). The coordination of arm
movements: an experimentally confirmed mathemati-
cal model. Journal of Neuroscience, 5:1688–1703.
Harris, C. M. and Wolpert, D. M. (1998). Signal-dependent
noise determines motor planning. Nature, 394:780–
784.
Jacobson, D. H. and Mayne, D. Q. (1970). Differential Dy-
namic Programming. Elsevier, New York.
Li, W. (2006). Optimal Control for Biological Movement
Systems. PhD dissertation, University of California,
San Diego.
Li, W. and Todorov, E. (2004). Iterative linear-quadratic
regulator design for nonlinear biological movement
systems. In Proc. 1st Int. Conf. Informatics in Con-
trol, Automation and Robotics.
Li, W. and Todorov, E. (2007). Iterative linearization meth-
ods for approximately optimal control and estimation
of non-linear stochastic system. International Journal
of Control, 80(9):14391453.
Scott, S. H. (2004). Optimal feedback control and the neu-
ral basis of volitional motor control. Nature Reviews
Neuroscience, 5:532–546.
Shadmehr, R. and Mussa-Ivaldi, F. A. (1994). Adaptive
representation of dynamics during learning of a motor
task. The Journal of Neurosciene, 14(5):3208–3224.
Shadmehr, R. and Wise, S. P. (2005). The Computational
Neurobiology of Reaching and Ponting. MIT Press.
Stengel, R. F. (1994). Optimal control and estimation.
Dover Publications, New York.
Thrun, S. (2000). Monte carlo POMDPs. In Solla, S. A.,
Leen, T. K., and M¨uller, K. R., editors, Advances
in Neural Information Processing Systems 12, pages
1064–1070. MIT Press.
Todorov, E. (2004). Optimality principles in sensorimotor
control. Nature Neuroscience, 7(9):907–915.
Todorov, E. and Jordan, M. (2003). A minimal intervention
principle for coordinated movement. In Advances in
Neural Information Processing Systems, volume 15,
pages 27–34. MIT Press.
Todorov, E. and Li, W. (2005). A generalized iterative LQG
method for locally-optimal feedback control of con-
strained nonlinear stochastic systems. In Proc. of the
American Control Conference.
Uno, Y., Kawato, M., and Suzuki, R. (1989). Formation
and control of optimal trajectories in human multijoint
arm movements: minimum torque-change model. Bi-
ological Cybernetics, 61:89–101.
Vijayakumar, S., D’Souza, A., and Schaal, S. (2005). In-
cremental online learning in high dimensions. Neural
Computation, 17:2602–2634.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
148
