QOS MULTICAST ROUTING DESIGN USING NEURAL
NETWORK
Ming Huang and Shang Ming Zhu
Department of Computer Science, East China University of Science and Technology, 200237 ShangHai, China
Keywords: Quality of service, Hopfield neural network, Multicast routing.
Abstract: In this paper, an algorithm based on Hopfield neural network for solving the problem of determining
minimum cost paths to multiple destination nodes satisfying QoS requirements is proposed. The schema of
constructing the multicast tree with HNN is emphasized after the analysis of the attributes of the multicast
tree. At last, the emulation explores the feasibility of this algorithm.
1 INTRODUCTION
With the rapid emergency of the multimedia
applications on networks, especially for video
conferences, the need for multicast QoS routing
mechanism to satisfy the multimedia transmission
requirements among conference participants is
urgently rising.
Wang and Crowcroft have proved QoS routing
with multi-constraint to be a NP-complete problem
(Wang et al., 1996). Neural networks have often
been formulated to solve NP-complete optimization
problems. Tank and Hopfield (Tank et al., 1986)
proposed the first neural approach applied in the
TSP problem. The advantage of the Hopfield NN is
the rapid computational capablility of solving the
combinatorial optimization problem. Ahn and
Ramakrishna (Ahn et al., 2001) proposed a near-
optimal routing algorithm employing a modified
Hopfield NN. In this paper, a new Hopfield NN
model is proposed to speed up the convergence
whilst improving the optimality of the multicast tree
constructed under multi-constraint
2 PROBLEM FORMULATION
As far as multicast routing is concerned, a network
is usually represented as a weighted directed graph
G=(V, E), where V, the set of vertexes, denotes the
set of nodes, and E, the set of directed edges,
corresponds to the set of links connecting the nodes.
Suppose the number of nodes is n, refer to the ith
node as i for short, then the adjacency matrix O
describing the initial state of the focused network
can be defined as: O
ij
=1, if the link from i to j exists;
elsewise, O
ij
=0.
We also appoint a node s
∈
V to denote the
source node of a multicast request. The source node
acts as the root of the multicast tree to be build
which has only out-degree. Correspondingly, let
d={d
1
,…,d
m
} ⊂ (V-{s}) denotes the set of the
destination nodes with only in-degree. Then the
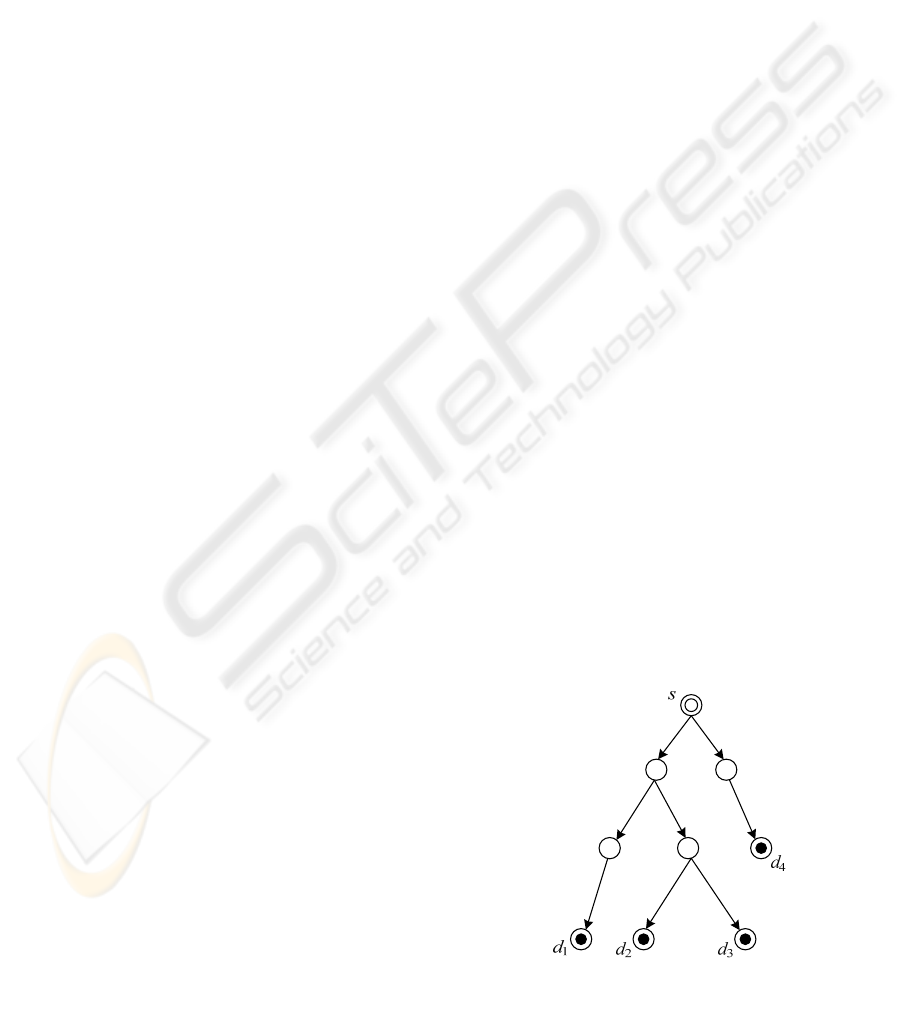
constructed multicast tree, denoted by T and shown
in Fig.1, should satisfy:
1) T is a subgraph of G;
2) The equal undirected graph T’ is a tree;
3) s is the root of T’;
4) d
∈
T and every leaf of T’ is in d;
5) Every vertex in T except s can be accessed
from s.
Figure 1: Indicating diagram of multicast tree.
213
Huang M. and Ming Zhu S. (2008).
QOS MULTICAST ROUTING DESIGN USING NEURAL NETWORK.
In Proceedings of the Fifth International Conference on Informatics in Control, Automation and Robotics - SPSMC, pages 213-216
DOI: 10.5220/0001476002130216
Copyright
c
SciTePress
Let the adjacency matrix A describing the
constructed subgraph G’ of G after multicast routing
is defined as: A
ij
=1, if the link from i to j is in G’;
elsewise, A
ij
=0. Then let’s prove the theorems
below:
Theorem 1. In a multicast tree T, there will be
one and only one path from s to v (v
∈
T and v≠s).
Proof: Existence. According to attribute 5) of T,
v can be accessed from s, so there is at least one path
from from s to d
i
(i=1,…,m);
Uniqueness. If there are two different paths from
s to v in T, then there will be at least two dis-
coincident sectors composed of directed edges in the
two paths. Combined with the joint vertexes, the two
sectors form a circle in the equal undirected graph of
T. Refer to attribute 2) of multicast tree, the
existence of the circle contradict the acyclic attribute
of a tree. So there is only one path from s to v in T;
Theorem 2. Supposing
s, d
∈
G’ and the in-
degree of s is 0, G’ is a multicast tree T if and only
if:
()
1
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∑
=
sj
n
k
k
A
, where j
∈
G’ and j≠s
(1)
()
01
2
'
2
1
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
∏
∑∑
∈
∈=
d
AA
d
Gj
dj
id
n
k
k
,
where i
∉
d or
0
'
>
∑
∈Gj
ij
A
(2)
Proof: Necessity. Based on the accessible theory
in graph theory, Eq.1 denotes the number of paths
from s to j within a length of k. Refer to Theorem 1,
Eq.1 is obviously tenable. If I
∈
T, then i must
locate at a branch of T except i is a leaf destination
node itself. Suppose the branch ends at a leaf θ.
According to Theorem 1, there is one and only one
path from s to θ and i is in the path. Due to attribute
4 of multicast tree, θ
∈
d, therefore Eq.2 is got.
Sufficiency. Obviously, attribute 1 of multicast
tree is qualified. Because of Eq.1, attributes 5 is
qualified. Considering the in-degree of s is 0, G’ is a
tree with s as the root, i.e. attributes 2 and 3 is
qualified. When Eq.2 is satisfied, for I
∈
G’, except
i is a leaf destination node itself , there will be at
least one leaf θ
∈
d which can be accessed from i by
one and only one path. So attribute 4 is qualified.
Therefore, G’ is a multicast tree.
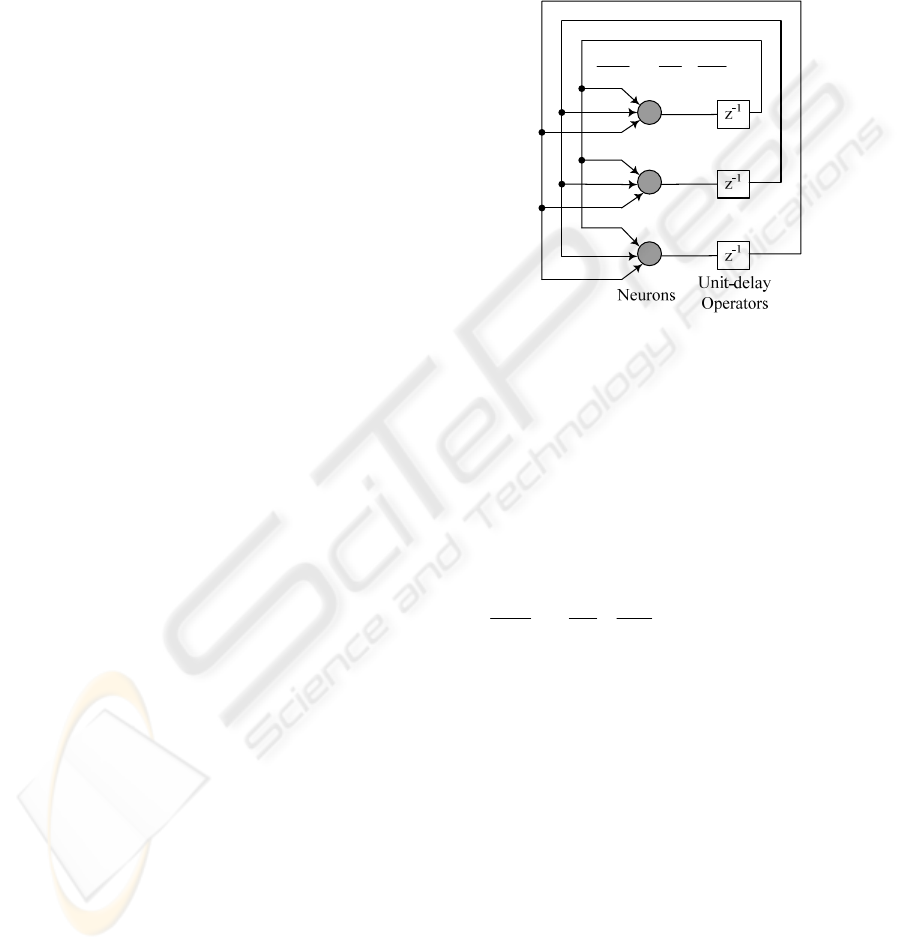
3 NEURAL NETWORK MODEL
The Hopfield NN model for multicast QoS routing,
which consists of
nn
×
neurons connected with
each other, is mapped from the corresponding
directed graph G of the aimed network system with
n nodes.
ij
V
ij
V
ij
V
ij
ijij
V
E
U
dt
dU
∂
∂
−−=
τ
Figure 2: Model of Hopfield neural network.
The output of the neuron at the position (i,j) is
denoted by V
ij
, where V
ij
=1, if the link from i to j
exists; otherwise, V
ij
=0. Obviously, the output
matrix V=[V
ij
]
n×n
is equal to the adjacency matrix A
of G. Let U
ij
denotes the input of neuron (i,j), and
define the gain function g of the neuron as:
()
1
1
=
⎟
⎠
⎞
⎜
⎝
⎛
∑
=
sj
n
k
k
A
, where j
∈
G’ and j≠s
(3)
ij
ijij
V
E
U
dt
dU
∂
∂
−−=
τ
(4)
Define several link state matrix as: W=[W
ij
]
n×n
,
B=[B
ij
]
n×n
, D=[D
ij
]
n×n
and L=[L
ij
]
n×n
, where W
ij
is the
cost of the link from i to j, B
ij
is the bandwidth of the
link from i to j, D
ij
is the delay of the link from i to j
and L
ij
is the parcket loss rate of the link from i to j.
The QoS constraints is denoted with B
w
, D
w
and L
w
where B
w
is the minimal available bandwidth of each
selected link, D
w
is the maximal available delay of
each selected path and L
w
is the maximal available
packet loss rate of each selected path.
As shown in Fig.2, the dynamic Eq.4 governs
the dynamics of the network. The design of the
energy function should reflect the attributes of the
selected multi-path below:
1) There is no non-existing link in the selected
multi-path;
2) There is no input to the source node in the
selected multi-path;
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
214
3) All destination nodes is in the selected multi-
path;
4) According to Theorem 2, the two equations
should be satisfied;
5) Satisfy the QoS constraints.
6) The total cost of the selected multi-path must
be as low as possible;
To fit the constraints above, we design the
suitable energy function as:
665544
332211
EEE
EEEE
μμμ
μ
μ
μ
+++
++=
(5)
()()
2
11
1
1
∑∑
==
−=
n
i
n
j
ijijij
VOVE
(6)
()
∑
=
=
n
i
is
VE
1
2
2
(7)
()
∑∑
∈=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
d
V
d
sd
n
k
k
E
2
1
3
1
(8)
()
()
⎟
⎟
⎟
⎠
⎞
⎟
⎟
⎠
⎞
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⎜
⎜
⎜
⎝
⎛
⎜
⎜
⎝
⎛
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
=
∑
∑
∏
∑
∑∑
∈
>
∑
∉
≠
∈
∈
=
≠
∈=
∈
2
0or
'
2
1
'
2
1
4
1
1
Vj
dj
i
si
Gi
d
id
n
k
k
sj
Gj
sj
n
k
k
Vj
ij
E
V
V
V
Ad
d
(9)
()
(
)
3215
zHzHzE ++=
(10)
() () ()
⎩
⎨
⎧
>
==
∫
e, otherwis
z, if z
zhdzzhzH
z
0
0
,
0
(11)
()
∑∑
=
≠
=
−=
n
i
n
ij
j
wijij
BVBHz
11
1
(12)
∑∑ ∑
=
≠
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−=
n
i
n
ij
j
n
k
jkijijw
VDVmDHz
11 1
2
(13)
()
())
w
n
i
n
ij
j
n
k
jkijij
Lm
VLVHz
−−
⎜
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
−=
∑∑ ∑
=
≠
==
1
1
11 1
3
(14)
()
∑∑
=
≠
=
=
n
i
n
ij
j
ijij
VWE
11
2
6
(15)
Obviously, E
1
, E
2
and E
3
refer to constraints 1, 2
and 3 respectively. According to Theorem 2, when
E
4
get minimal (i.e. zero), the constraint 4 is
attained. E
5
represents the integration of QoS
constraints on bandwidth, delay and loss rate. As z
1
,
z
2
and z
3
represents the deviation of the QoS
constraints and the minus value is meaningless, so
we filter the minus value with an integral
computation in E
5
. With z
1
, z
2
and z
3
, conditions of
links near root will influence the deviation more
severely.
4 EMULATION
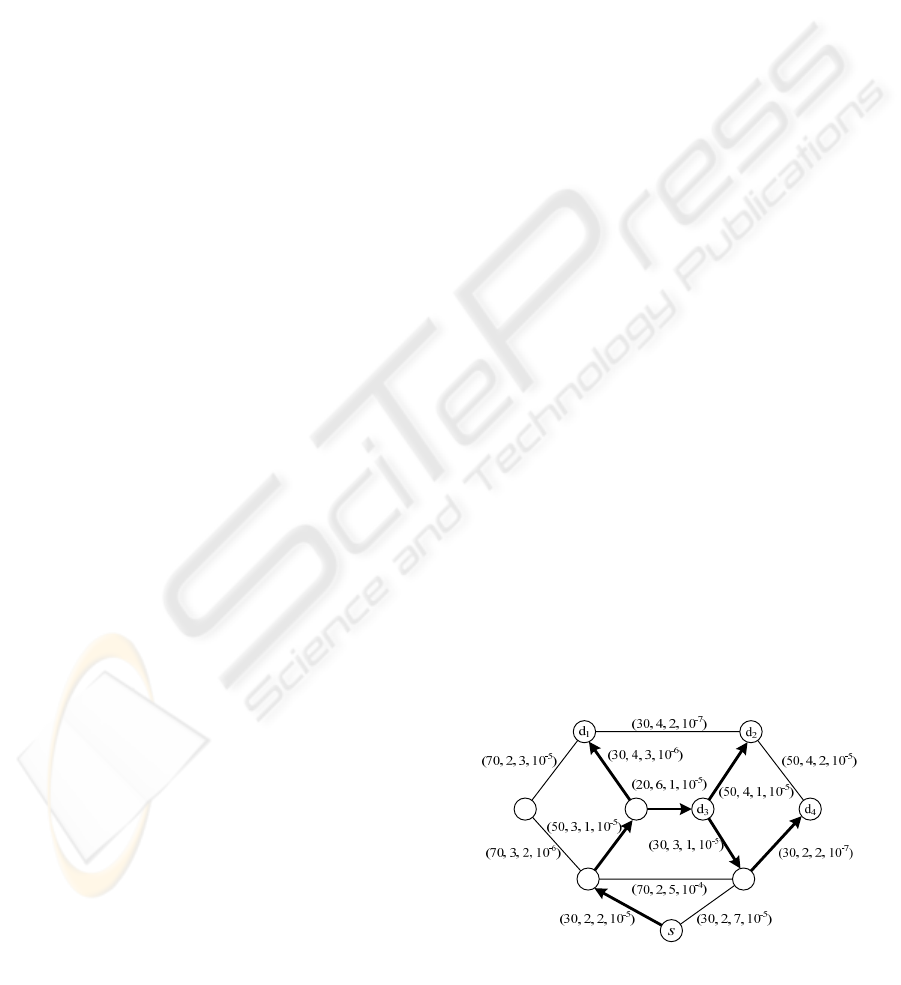
Fig.3 shows the topology of the delegating network
system. The source node which promotes the routing
request and four destination nodes have already been
signed out in the graph. Each link in the network is
labeled with a link status vector consists of cost W,
bandwidth B(MB), delay D(ms) and loss rate L. The
QoS constraints are: B
w
=2MB, D
w
=8ms, L
w
=10
-3
.
In this case, we set coefficient μ
1
=80000, μ
2
=40000, μ
3
=160000, μ
4
=500, μ
5
=400, μ
6
=400,
λ=1, and Δt = 2×10
-8
. By emulation, we could obtain
the global optimal solution shown in Fig.3.
5 CONCLUSIONS
In this paper, we propose a new multicast tree
selection algorithm to simultaneously optimize
multiple QoS parameters which is based on Hopfield
neural network. The result of emulation shows that
the utilization of Hopfield neural network is an
available method to solve QoS routing problems.
Furthermore, by the massive parallel computation of
neural network, it can find near optimal route
quickly, so the real-time requirement of routing in
high-speed network system could be satisfied.
Figure 3: Topology of network system with parameters
and selected multi-path.
QOS MULTICAST ROUTING DESIGN USING NEURAL NETWORK
215

REFERENCES
Wang Z, Crowcroft J, 1996. Quality of service for
supporting multimedia applications. 14th. IEEE JSAC.
Tank, D.W., Hopfield, J.J, 1986. Simple neural
optimization networks: an A/D converter, signal
decision network, and a linear programming circuit.
33th. IEEE Transactions on Circuits and Systems.
Ahn, C.W., Ramakrishna, R.S., Kang, C.G., Choi, I.C.,
2001. Shortest Path Routing Algorithm Using Hopfield
Neural Network. 37th. Electronics Letters.
B.M. Waxman, 1988. Routing of multipoint connections.
Vol.9. IEEE TSAC.
S.Chen, K.Nahrstedt, Y.Shavitt, 2000. A QoS-aware
multicast routing protocol. Vol.18. IEEE Journal on
Selected Areas in Communications.
Q.Sun, 1999. A genetic algorithm for delay-constrained
minimumcost multicasting. Technical Report. IBR. TU
Braunschweig. Braunschweig. Germany.
ICINCO 2008 - International Conference on Informatics in Control, Automation and Robotics
216
