
CONTROL POLYGON BASED TEXTURE SYNTHESIS ON
BIQUADRATIC BĒZIER RATIONAL SURFACES
Rupesh N. Shet, H. E. Bez and E. A. Edirisinghe
Department of Computer Science, Loughborough University, UK
Keywords: Texture synthesis Discrete Wavelet Transform (DWT), EZW, Rendering, Bézier surfaces.
Abstract: Existing texture synthesis algorithms fail to deliver effectively in application areas where progressive
rendering of texture is required. To provide a practical solution to this problem we propose a novel
algorithm for progressive-texture synthesis on surfaces, which makes use of the Embedded Zero-tree of
Wavelet (EZW) idea proposed by Shapiro et al., 1993 which is capable of prioritising the coefficients of a
DWT decomposed image according to their visual significance. We demonstrate the use of the proposed
algorithm on texturing a single biquadratic surface and two smoothly joined biquadratic surfaces. It is
further shown that the proposed texture synthesis approach on Bézier patches allows the algorithm's general
use in texture synthesis on many common surface topologies and can be generalised for arbitrarily shaped
surfaces. We provide experimental results to prove the effectiveness of the proposed approach, when
synthesising textures of regular, irregular and stochastic nature. Further experimental results are provided to
illustrate the practical use of the proposed texture synthesis algorithm in resource constrained application
domains.
1 INTRODUCTION
Texture synthesis provides a practical solution for
data acquisition and is often used to enhance realism
of artificially created scenes. As result, a number of
‘image based' texturing algorithms have been
proposed in the past decade. A typical texture
synthesis algorithm starts from a sample image and
attempts to produce a larger texture with a visual
appearance similar to the sample, by repeated
placement of micro patterns of texture elements. It
does this in a way that when perceived by an
observer, the synthesized texture appears to be
generated by the same underlying stochastic process.
However all texture synthesis algorithms are
challenged by the high statistical variability of
textures involved in synthesis. Thus a universal
solution to fast texture synthesis yet remains an open
problem. Texturing surfaces provides further
challenges and attracted much research interest in
the recent past due to applications in computer
graphics, animated movie production, computer
games, education, architecture, computer art and
virtual productions.
A major proportion of research in the area of
texture synthesis has focused on synthesizing texture
on planner surfaces. Recently a number of
approaches have been proposed for texture synthesis
on surfaces. These texture synthesis approaches can
be broadly classified into two groups, namely, pixel
based (Wei & Levoy, 2000, 2001; Turk, 2001;Ying
et al., 2001; Ashikhmin et al., 2001; Tong et al.,
2002; Shet et al., 2006; Lefebvre and Hoppe, 2006 )
and patch based ( Neyret and Cani, 1999; Praun et
al., 2000; Soler et al., 2002; Sebastian et al., 2003;
Wang et al., 2005; Wing Fu et al., 2005) approaches.
Pixel based approaches consider a pixel as the basic
unit in the synthesis process. Patch based approaches
are an alternative to pixel based approaches where
an attempt is made to synthesis texture by copying
selected regions of pixels from the sample texture
and stitching them together. This approach
overcomes the limitations of the pixel based
approaches, i.e. being limited to work with certain
types of textures and the lack of computational
speed. Neyret-Cani’s 1999, technique is based on
precomputed triangular texture samples which are
mapped non-periodically. However this method is
restricted to synthesising isotropic textures. In the
lapped texture technique proposed by Praun et al,
2000, the texture patches are first oriented and are
subsequently placed in an overlapping fashion on a
45
N. Shet R., E. Bez H. and A. Edirisinghe E. (2008).
CONTROL POLYGON BASED TEXTURE SYNTHESIS ON BIQUADRATIC BÄŠZIER RATIONAL SURFACES.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 45-52
DOI: 10.5220/0001096400450052
Copyright
c
SciTePress

surface with a predefined vector field. The method
works for a limited set of textures. Soler et al., 2002
introduces hierarchical texturing to overcome
drawbacks of previous algorithm. The method is
capable of capturing low-frequency pattern while
preserving high frequency randomness in the
texture. The synthesis time may vary from few
minutes to few tens of minutes. Sebastian et al.,
2003 separated the texture pre-processing from
synthesis and proposed two independent phases. Pre-
processed texture is stored on a disk and used when
needed. This process is very slow but only needs to
be performed once. The pre-processing time vary
from minutes to a few tens of minutes. Further
storing the texture on a disk is essential. Wang et al.,
2005 algorithm is mainly based on global conformal
parameterization of surfaces, where the textures are
preserved on surfaces without seams or cracks. This
algorithm is simple for texture synthesis but
parameterization process adopted is time consuming
thereby slowing down the overall performance.
Wing Fu et.al., 2005 introduced the concept of
Wang tiles. Initially a low distortion conformal map
is created from the input surface, which forms a
quad based geometry. The texture is then laid out on
quad surfaces, properly oriented and then mapped
back on to the surface. However this approach
inherits all drawbacks of the image quilting
algorithms.
All the above techniques are applied on irregular
shapes of triangular meshes, which results in seams
at edges. Size of triangles in the mesh also varies
which makes the visual artefacts on the surface,
prominent. Further to this, it will also use extensive
bandwidth in transmission media as triangular mesh
information and texture are in uncompressed format.
Further the animation of this triangular mesh is
difficult as they are rigid. To overcome many of the
above problems we have proposed to use NURBS, a
form of surface representation which helps to
compress a mesh and thus can be applied in
constrained bandwidth environments. NURBS also
provides additional facilities to animate the surface.
The inspiration of our work comes from the
present requirements for progressive texture
synthesis on surfaces, which results in extensive use
of transmission media with limited bandwidth for
modern application domains such as remote
visualisation, distributed/collaborative gaming etc.
Current texture synthesis algorithms on surfaces are
time consuming and fail to perform in
progressive/transform domain. To overcome this
problem we propose a progressive texture synthesis
algorithm using multiresolution DWT
decomposition, coefficient prioritisation using EZW
(embedded zero-tree wavelet) algorithm and surface
representation using biquadratic rational surfaces
which is falls under patch base category. We prove
the proposed novel algorithm is capable of creating
seamlessly varying quality levels of synthesized
texture on surfaces. According to the authors
knowledge it is a first attempt that demonstrates
progressive texture synthesis on meshes, which
utilises control polygons generated from the
biquadratic Bézier equations. We show that the
proposed work can be generalised to any type of
arbitrary mesh.
For clarity of presentation the paper is organised
as follows Section-2 introduces the reader to the
research background and fundamentals. Section-3
presents the proposed algorithm. Section-4 provides
experimental results and a detailed analysis. Finally,
Section-5 concludes, with an insight to possible
improvements and future variations.
2 RESEARCH BACKGROUND
For the purpose of clarity and ease of reference we
have summarized the fundamental techniques used
for multiresolution representation of texture (DWT)
(Wickramanayake et al., 2005), DWT coefficient
prioritization (EZW) (Shapiro et al., 1993) and
surface parameterization (biquadratic rational
surfaces) in this section. Hence readers who are
familiar with these concepts can forgo reading this
section.
2.1 DWT Representation of Texture
Image
Textured images contain a large amount of
perceptual data. Therefore the number of bits
required to represent/encode a texture image is high.
However typical images consist of a wide range of
frequency components spread throughout the human
visual frequency band. Some of theses frequency
components have a significant effect in human
perception while some others have very low
significance. Fortunately texture images are often of
this type. The Discrete Wavelet Transforms (DWT)
provide a compact multi resolution representation of
an image. It gives a signal representation in
correspondence to a narrow band, low frequency
range and some of the coefficients represent short
data lags corresponding to a wide band, high
frequency range. Using the concept of scale, data
representing a continuous trade off between space
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
46

and frequency can be made available for further
processing.
Figure 1: Transforming the sample texture into a multi-
resolution image representation. (a) Sample texture, (b)
single level decomposition, (c) two level decomposition,
(d) three level decomposition.
In our algorithm we use two-dimensional DWT.
To begin with, the texture image is subdivided into
four sub-bands using horizontal and vertical DWT
filters over the image pixels. The resulting sub bands
labeled LH1, HL1 and HH1 represent the finest
scale wavelet coefficient whereas the sub-band
labeled LL1 represents low resolution coefficients.
In order to obtain the next level of wavelet sub-
bands, the sub band labeled LL1 is further
decomposed and sampled using the vertical and
horizontal DWT filters. This process is repeated
until the required final decomposition is reached (see
Figure 1). The coefficients of the subbands are then
used for speeding up searching process and
prioritized using the EZW algorithm presented next.
2.2 Embedded Zerotree Wavelet
(EZW) Algorithm
The Zerotrees of wavelet coefficient concept was
originally introduced by Shapiro et al., 1993 in
progressive encoding of images. It is based on two
important observations:
1. Natural images in general have a low pass
spectrum. Therefore when an image is
wavelet transformed the energy in the
subbands decreases as the scale decreases
(low scale means high resolution), so the
wavelet coefficients will, on average be
smaller in the higher subbands than in the
lower subbands.
2. Large wavelet coefficients are visually more
important than smaller wavelet coefficients.
EZW provides a compact representation of
perceptually significant coefficients and multi
resolution construction capability of an image. The
idea is to organize DWT coefficients of an image
(see Figure 1) in a prioritized order of visual
significance, depending on their position and
magnitude in the DWT decomposition and to
subsequently encode the ordered list of coefficients
following an embedded coding algorithm. In an
embedded coding algorithm the encoder can
terminate the encoding at any point thereby allowing
a target bit rate or target distortion metric to be met
exactly. On the other hand, given a bit stream, a
decoder can cease decoding at any point in the bit
stream. Thus it is capable of producing exactly the
same image that would have been encoded at the bit
rate corresponding to the truncated bit stream.
In this paper we use the EZW algorithm’s initial
coefficient prioritization procedure to prioritize their
use within texture synthesis algorithm. Due to space
limitation we refer readers interested in the detail of
the EZW coefficient prioritization algorithm to
Shapiro et al., 1993. We show that the visually
prioritized availability of coefficients enables
seamless progressive texture synthesis capability on
biquadratic rational surface using control polygon.
This is the main contribution of our present work.
2.3 Biquadratics Bézier Surfaces
This section will briefly introduce biquadratic
surface patches and construction of simple surface
using them. For more details the readers are referred
to Bez H.E, 2006.
Rational parametrisation is a de-facto standard
representation in computer graphics and geometric
modelling software, allowing portability across
applications and systems. In addition to possessing
desirable geometric properties, rational
parametrisation
♦ requires the evaluation of only polynomial
functions,
♦ gives rise to a compact data-structure,
♦ facilitates interactive control of shape,
♦ is complete in the sense that approximation
of any shape to a specified tolerance δ can
CONTROL POLYGON BASED TEXTURE SYNTHESIS ON BIQUADRATIC BÉZIER RATIONAL SURFACES
47
be achieved, and exact parametrisation (i.e.
δ= 0) is often possible.
Rational parametrisations of surfaces comprise
local atlases, or patches, of the form:
()
(
)
() ()
(2.1)1,ts,0,
st
st
t)τ(s,
n.m
0jk,
jk,m.jn.k
n.m
0jk,
*
jk,m.jn.k
ωbb
vbb
<<=
∑
∑
=
=
where
ω
jk ,
are the weights and
v
jk ,
are the
Bernstein vectors. If all the weights are non-zero this
may be expressed as
()
()
()
()
)2.2(1t,s0,)t,s(
m.n
0j,k
j,kj.mk.n
m.n
0j,k
j.mk.n
st
st
bb
bb
j,k
j,k
<<=
∑
∑
=
=
ω
ω
ν
τ
where
ω
jk
jk
jk
v
v
,
*
,
,
=
are the Bézier vertices. The values of
n and m determine the degree of the
parametrisation; if n = m = 2 the patch is said to be
biquadratic and if n = m = 3 it is bi-cubic.
With given nine control points we compute and
draw the biquadratic surface patch defined by them.
(see Figure 2)
(a) (b)
Figure 2: (a) Green Colour: Biquadratic control polygon
point, Red Colour: Smooth surface mesh generated using
control polygon (b) Control polygon mesh (for 9 control
points generate 4 faces).
Many of the desirable geometric properties of
rational representation, e.g. the convex hull property
and the existence of bézier vertices, are lost if
negative or zero weights occur - hence, in computer
graphics and geometric modelling applications,
positive weight parametrisations are always
preferred. For computational efficiency, low degree
parametrisations are desirable.
3 PROPOSED METHODOLOGY
In this section we provide the design details of the
proposed texture synthesis algorithm.
3.1 Texture Synthesis on Control
Polygon
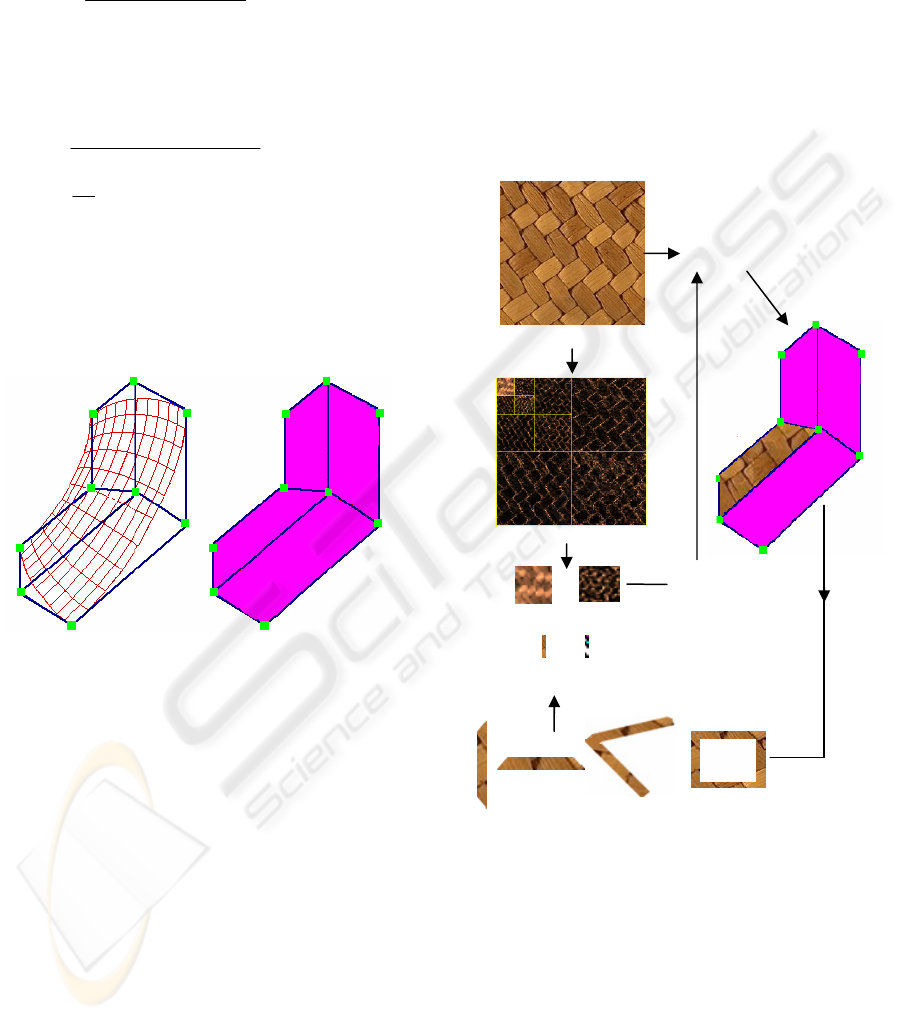
Figure 3 illustrates the basic block diagram of the
proposed algorithm. The texture synthesis process
starts by applying a n-level (n=3 used in our
experiments) 2D DWT (e.g. Haar Transform) on
sample texture image, which is denoted as I
sample
,
The application of single level 2D DWT on the
sample texture results in a set of component images
i.e. sub-bands, as follows:
(
)
(
)
)1.3(DWT,,,
IIIII
sample1HH1LH1HL1LL
−
=
Figure 3: Proposed block diagram for texture synthesis on
biquadratic surfaces.
Where
IIII
HHLHHLLL 1111
,,,
are the texture image
sub-bands corresponding respectively to low-
resolution approximation, vertical details, horizontal
details and diagonal details of sample texture.
Similarly 2
nd
level and 3
rd
level decomposition are
obtained by applying DWT to the low-resolution
sub-bands of previous decomposition level. This can
be mathematically represented as follows.
(
)
(
)
)2.3(,,,
12222
−=
IIIII
LLHHLHHLLL
DWT
Sample
LL3 and HH3
3
rd
Levelled DWT
LL3 and HH3 bands
Paste block of shape and
size of face on control
polygon /
EZWIDWT
Best Match
Location
Find next best match
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
48

(
)
(
)
)3.3(,,,
23333
−=
IIIII
LLHHLHHLLL
DWT
(
)
(
)
)4.3(,,,
1111
−=
++++
IIIII
LLnHHnLHnHLnLLn
DWT
from n-level we extract low-resolution and diagonal
detail bands i.e.
I
LLn
and
I
HHn
.
We generalise the notation used in equation
(3.1)-(3.6)as
I
pl
where
}{
HHLHHLLLp ,,,
∈
and
}{
n,..2,1,0l ∈ where p represent the sub-bands
within each decomposition level (LL-low resolution,
LH-horizontal, HL- vertical, HH diagonal) and l
represent the decomposition level. DWT represent
the forward discrete wavelet transform.
The basic idea of proposed algorithm is to
synthesise texture on control polygons of a given
surface. Let
B
yxLLn ),(
represent a general polygonal
block of decomposed sample image located at
position (x, y) relative to the sub-bands (p, l)’s
origin.
Initially we randomly pick block
B
yxLLn ),(
from
the sample texture image with identical size and
shape to that of the control polygon face. This
randomly created texture block is mapped to the
control polygon surface shown in figure 3. [Note:
the details of the mapping process are described in
section 3.2.]
In locating the next block to be synthesized, we
cut a 8 pixel wide template of pixels along the edge
of already synthesized, neighbouring blocks, apply a
3 level DWT decomposition on the template block
and extract low-resolution and diagonal detail bands
which are used for searching in sample LL3 and
HH3 bands. Best matching block can be found by
minimizing the L2 norm. EZW algorithm can be
used if coefficient prioritisation is used to further
reduce complexity.
In general, if
)1,1( yxpl
B
and
)2y,2x(pl
B
are two
randomly shaped blocks to be matched, we
say
)1,1( yxpl
B
is the best match for
)2,2( yxpl
B
if
),(
)2,2()1,1( yxplyxpl
BBd
is minimum for all
possible
pl
B blocks, which is calculated as,
)5.3(
}])i(B)i(B[
])i(B)i(B[{
)B,B(d
Bi
2
)2y,2x(3HH)1y,1x(3HH
2
)2y,2x(3LL)1y,1x(3LL
)1y,1x()2y,2x(
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂−∂+
∂−∂
=
∑
∂∈
Where
pl
B∂ an edge is zone of block
),( yxpl
B
and
i is an element (coefficient) within the edge
zone.
Finally the overlap area of the best matching
edge is blended with the overlap area on the original
block using alpha bending. The non-overlapping
area of the block is picked from the sample texture
and subsequently appended to the synthesized
texture. This process will continue till all the faces
of control polygon are mapped. In some cases we
have considered two or more overlapping areas for
finding the best match.
3.2 Texture Mapping on Control
Polygons
In our implementation initially we create
propagating seed vertex directions, which are then
used to smooth the surface vector field. However
alternatively a number of other surface vector field
techniques (Wei-Levoy, 2001; Turk 2002; Ying etal,
2001) can be used to replace the approach we have
selected above. Once vector fields are assigned to
all control polygon faces, we then rotate all the faces
according to tangential vector field and surface
normal, thus placing all faces in the same 2D plane.
Using a modified version of Soucy et al., 1996,
approach (Note: modified from using triangle to
using polygon) a texture map. T is created. For each
face of the control polygon, we map it to a
corresponding face in T in compact form, i.e. with
no space being wasted. The faces in T are textured
using the corresponding best matching block. The
faces in T that we use are of non-uniform size that
are a better fit to the shape and size. It is noted that
the resulting texture can be rendered on the control
polygon surfaces at interactive rates. The images
illustrated in Figure 4 were rendered in this manner
using 256 x 256 textures. The models used in our
experiments are composed of smooth surfaces
having between 100 to 1000 faces, whereas the
control polygons used consisted of 4 faces to 8 faces
(It can be further increase to n faces). We have
observed that these surfaces render at real-time rates.
3.3 Projection of Texture from Control
Polygons to Biquadratic Rational
Surfaces
Firstly we calculate the distance between control
points of the control polygon using the standard
distance formula between two points in 3D space.
Depending on these distances we calculate relative
location of projections of these points on the rational
surface, parameterised by
0,1
s
t<<
. Using the
correspondence between points we then decide on
the area projection from control polygonal mesh to
the smooth surface. Figure 4(a) illustrates the texture
synthesized onto the control polygon using the
CONTROL POLYGON BASED TEXTURE SYNTHESIS ON BIQUADRATIC BÉZIER RATIONAL SURFACES
49

proposed algorithm and figure 4(b) illustrates the
mapped texture onto the smooth rational surface..
Figure 4: (a) Texture on control polygon (b) Projection
from control Polygon to smooth surface.
Note that closer the control polygon to the smooth
surface representation, lesser distortion in projection
will occur and vice –versa.
3.4 Progressive Texture Using EZW
In order to achieve progressive texture synthesis on
surfaces, we adopt Shapiro’s EZW idea in which
coefficient values with magnitudes above a given
threshold are considered significant. This threshold
(t) is calculated using equation (3.6) based on the
magnitude of wavelet coefficients of decomposed
sample image.
()
)6.3(Kt
2
y,xMAX
LL
log
n
2
−=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
where MAX() means the maximum coefficient
value, K is a constant and
()
yx
LL
n
, denotes a
general coefficient in
LL
n
sub-band. By only
considering the coefficients of sub-bands, which are
larger than the threshold and ignoring all others (i.e.
setting to zero), an inverse DWT is calculated to
produce the texture at a given progressive texture
quality. This can be expressed generally as:
()
)7.3(
thershold
,,
,
EZWIDWT
BB
BB
B
HHnHLn
LHn,LLn
1LLn
−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
=
−
The above equation can produce discrete quality
levels of texture depending on threshold or number
of coefficients need to be considered. Image quality
can be increased by decreasing the threshold and
vies-versa. Note that the function EZWIDWT above
represent an EZW constrained inverse discrete
wavelet transform. When progressive texture
synthesis is required we replace the normal texture
mapping process with the above EZW based
approach (see figure 5 & 6).
4 EXPERIMENTAL RESULTS &
ANALYSIS
In order to analyse the performance of proposed
algorithm and to show that surfaces can be rendered
effectively, we have implemented the proposed
algorithms in OpenGL, C++.
Experiment were performed on a diverse range
of texture samples that include regular, near-regular,
irregular and stochastic (Lin et al., 2004) textures.
Results illustrated in figure 5 indicate the ability of
proposed technique to efficiently map and
synthesized texture on surfaces, with minimal
artifacts. Further as matching and searching is
performed in wavelet domain, the texture synthesis
is fast. Textures illustrated in Figure 5 (a), (b), (c)
respectively belong to near-regular, regular, and
stochastic categories. Similar synthesized quality
levels are demonstrated for all three texture
categories. Further analysis revealed that the time
required to synthesize these texture is in the range of
few milliseconds.
To further extend the functionality of the
proposed method, we have extended our work to
progressive texture synthesis on surfaces. We have
preformed a wide range of experiments (see figure 6
& 7) to show that texture can be synthesized at
seamlessly different levels of quality on surfaces,
without consuming noticeable processing time.
Figure 6 illustrates the synthesis of a stochastic
texture of a flower. It is evident from the results that
only 10% of information from sample texture is
sufficient to create a texture with sufficiently rough
quality. By increasing the percentage of coefficients
further, the quality of the synthesized texture can be
seamlessly improved. Further experiments revealed
that for this texture, 20% of coefficients was
sufficient to synthesize a texture visually equal to
the texture that can be synthesized when all
coefficients are utilized. Progressive texture
synthesis gives the added advantage of being able to
truncate a bit stream representing the sample texture
at any intermediate stage, still being able to
synthesize texture at some intermediate quality level.
To further illustrate the application of the
proposed idea, we have extended our approach to
synthesizing texture on two smoothly joined
biquadratic rational surfaces, shown in figure 7.
Figure 7(c) shows two smoothly join biquadratic
patches. Figure 7(d) to 7(k) illustrates progressive
texture synthesis on this surface. This proves that
our technique can be extended to the many
geometric topologies. Results in figure 7 further
illustrates using regular and near-regular texture
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
50

samples that texture variations across patch
boundaries are smooth.
Figure 5: Texture synthesis on biquadratic surface.
5 CONCLUSIONS
We have introduced a novel DWT based approach to
synthesizing, texture and progressive texture, on
biquadratic surfaces. We have presented the methods
and algorithms in detail along with possible
applications and advantages. The proposed method
has the capability of synthesizing texture at
seamlessly different quality settings, a functionality
which is not possible via existing state-of –the art
techniques.
The use of visual prioritisation of information in
the sample image during texture synthesis allows the
task to be carried out at a higher speed but at an
equivalent visual quality level. We show that the
proposed approach is computationally efficient,
results in good quality texture synthesis, and is
applicable in bandwidth-adaptive/compressed-
domain applications such as remote visualization.
We have shown that the control polygon strategy
used can be extended to cover synthesizing texture
on many 3D objects with arbitrary surface topology.
We are currently in the process of generalizing the
proposed algorithm to address this issue.
Figure 6: Stochastic progressive texture on biquadratic
surface.
a1-3% coefficients
a2-5% coefficients
a3-10% coefficients
a4- ALL coefficients
(a) near-regular
(b) regular
(c) stochastic
CONTROL POLYGON BASED TEXTURE SYNTHESIS ON BIQUADRATIC BÉZIER RATIONAL SURFACES
51
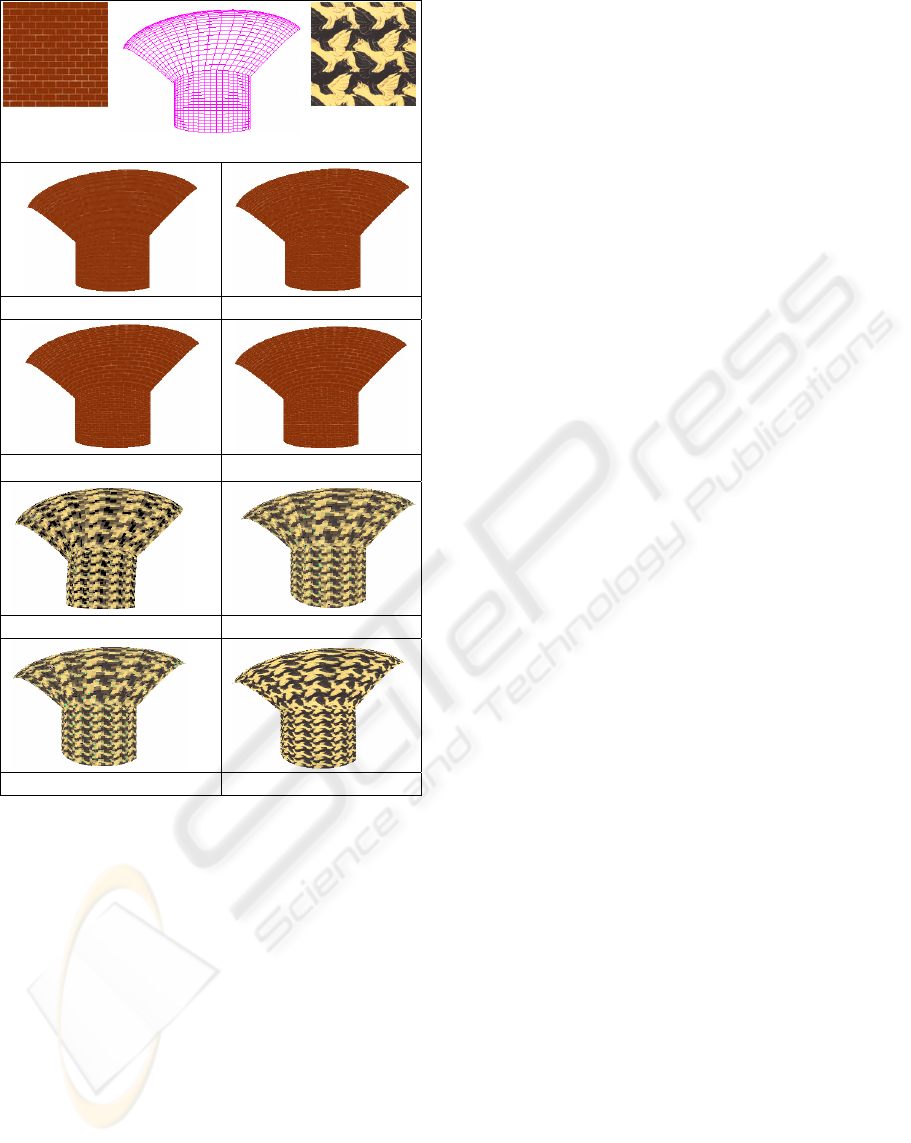
Figure 7: Progressive texture on two-joined biquadratic
surface.
REFERENCES
Ashikhmin, M., Synthesizing natural textures, ACM
Symp. on Interactive 3D Graphics (March), 217–
226, 2001.
Bez H.E., Bounded domain, bi-quadratic rational
parametrisations of Dupin cyclides, Report No.
1090, 2006, Dept of CS, Loughborough University.
Chi-Wing Fu and Man-Kang Leung,Texture Tiling on
Arbitrary Topological Surfaces in Proceedings of
Eurographics Symposium on Rendering 2005
(EGSR 2005), Germany,2005, pp. 99-104.
C. Soler, M.-P. Cani, and A. Angelidis, Hierarchical
Pattern Mapping Proceedings of Siggraph 2002, vol.
21, no. 3, pp. 673-680, 2002.
Heeger, David J. and James R. Bergen, Pyramid-Based
Texture Analysis/Synthesis, In proceeding of
SIGGRAPH 95, Aug., 229–238, 1995.
J. M. Shapiro, Embedded Image Coding Using Zerotrees
of Wavelet Coefficient”, IEEE Trans. Signal
Processing, December, VOL 41(no.12), 3445-3462,
1993.
Lujin Wang, Xianfeng Gu, Klaus Mueller, Shing-Tung
Yau: Uniform texture synthesis and texture mapping
using global Parameterization,, Volume 21, Numbers
8-10, September 2005, Pages: 801 - 810 Special
Issues of Pacific Graphics 2005.
Neyret F., and Cani, M.P., Pattern-based texturing
revisited, Proc. of SIGGRAPH 99, 235–242, 1999.
Praun E., Finkelstein, A., and Hoppe, H., Lapped
textures, Proceedings of SIGGRAPH 00, 465–470.
Rupesh N. Shet, Eran A. Edirisinghe, and Helmut E.
Bez. Progressive texture synthesis on 3D surfaces.
In Proceedings of VIIP06 Sixth international
conference, pages 136–141, 2006.
Soucy, Marc, Guy Godin and Marc Rioux, A Texture-
Mapping Approach for the Compression of Colored
3D triangulations, The Visual Computer, Vol. 12,
No. 10, 1996, pp. 503–514.
Sebastian Magda, David Kriegman, Fast Texture
synthesis on Arbitrary meshes, Proceedings of the
14th Eurographics workshop on Rendering Vol. 44,
pp: 82 - 89 ,2003.
Sylvain Lefebvre and Hugues Hoppe. Appearance-space
texture synthesis. ACM Trans. Graph., 25(3):541–
548, 2006. ISSN:0730-0301.
Tong Xin , Jingdan Zhang, Ligang Liu, Xi Wang,
Baining Guo, Heung- Yeung Shum, Synthesis of
Bidirectional Texture Functions on Arbitrary
Surfaces, SIGGRAPH 2002, Pages: 665 – 672.
Turk, G., Texture synthesis on surfaces, Proc. Of
SIGGRAPH2001, 347–354, 2001(August).
Wickramanayake, D.S., Edirisinghe, E.A., Bez H.E.,
Multiresolution texture synthesis in wavelet
transform domain, The Journal of Imaging Science
and Technology 2005.50(1):93-102, 1 2006.
Wei L.-Y., and Levoy, M., Fast texture synthesis using
tree-structured vector quantization, Proc. of
SIGGRAPH 2002, 479–488.
Wei L.-Y., and Levoy, M., Texture synthesis over
arbitrary manifold surface, Proceed of SIGGRAPH
2001
, 355–360, 2001.
Wen-chieh Lin, James Hays, Chenyu Wu, Vivek
Kwatra, Yanxi Liu, A comparison study of four
texture synthesis algorithm on near-regular textures.
Tech. Report CMU-RI-TR-04-01, Robotics Institute,
Carnegie Mellon University, 2004. Also appeared in
Poster Session SIGGRAPH, August 2004.
Ying, L., Hertzmann, A., Biermann H., and Zorin, D.,
2001, Texture and shape synthesis on surfaces,
Eurographics Rendering Workshop, 301–312, 2001.
(a) near-regular
(b) regular
(c) smoothly joint mesh
(d) – 1% coefficients (e) – 2% coefficients
(f) – 6% coefficients
(g) ALL coefficients
(h) – 2% coefficients (i) – 4% coefficients
(j) – 6% coefficients (k) ALL coefficients
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
52
