ANALYSIS OF POINT CLOUDS

Using Conformal Geometric Algebra

Dietmar Hildenbrand

Research Center of Excellence for Computer Graphics, University of Technology, Darmstadt, Germany

Eckhard Hitzer

Department of Applied Physics, University of Fukui, Japan

Keywords:

Geometric algebra, geometric computing, point clouds, osculating circle, ﬁtting of spheres, bounding spheres.

Abstract:

This paper presents some basics for the analysis of point clouds using the geometrically intuitive mathematical

framework of conformal geometric algebra. In this framework it is easy to compute with osculating circles

for the description of local curvature. Also methods for the ﬁtting of spheres as well as bounding spheres are

presented. In a nutshell, this paper provides a starting point for shape analysis based on this new, geometrically

intuitive and promising technology.

1 INTRODUCTION

The main contribution of this paper is its collection

of properties and basic algorithms that make it a very

promising tool for the analysis of point clouds. Please

refer for instance to (Schnabel et al., 2007) for current

research results concerning this application.

Conformal geometric algebra has shown some ad-

vantages in recent years. It is very easy to calculate

directly with geometric objects like spheres, circles

and planes. Also transformations can be handled very

easily. This mathematical framework is able to unify

a lot of mathematical systems like vector algebra, pro-

jective geometry, quaternions or Pl¨ucker coordinates.

While geometric algebra formerly had the prob-

lem of efﬁciency, now there are approaches available

so that algorithms written in this framework can even

be faster than conventional algorithms (see (Hilden-

brand et al., 2006)).

Like implementations of quaternions can be

more robust than rotation matrices geometric algebra

promises to deliver more robust algorithms. As an ex-

ample, planes can be represented as speciﬁc spheres

allowing to ﬁt spheres or planes into point sets (see

(Hildenbrand, 2005)).

2 FOUNDATIONS OF

CONFORMAL GEOMETRIC

ALGEBRA

Blades are the basic computational elements and the

basic geometric entities of the geometric algebra. For

example, the 5D Conformal Geometric Algebra pro-

vides a great variety of basic geometric entities to

compute with. It consists of blades with grades 0, 1,

2, 3, 4 and 5, whereby a scalar is a 0-blade (blade of

grade 0). There exists only one element of grade ﬁve

in the Conformal Geometric Algebra. It is therefore

also called the pseudoscalar. A linear combination of

blades is called a k-vector. So a bivector is a linear

combination of blades with grade 2. Other k-vectors

are vectors (grade 1), trivectors (grade 3) and quad-

vectors (grade 4). Furthermore, a linear combination

of blades of different grades is called a multivector.

Multivectors are the general elements of a Geometric

Algebra.

Table 1 presents the basic geometric entities of

conformal geometric algebra, points, spheres, planes,

circles, lines and point pairs. The s

represent dif-

ferent spheres and the π

different planes. The two

representations are dual to each other. In order to

switch between the two representations, the dual op-

erator which is indicated by ’

∗

’ (division by the

pseudoscalar), can be used. For example in the stan-

Hildenbrand D. and Hitzer E. (2008).

ANALYSIS OF POINT CLOUDS - Using Conformal Geometric Algebra.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 99-106

DOI: 10.5220/0001094100990106

 SciTePress

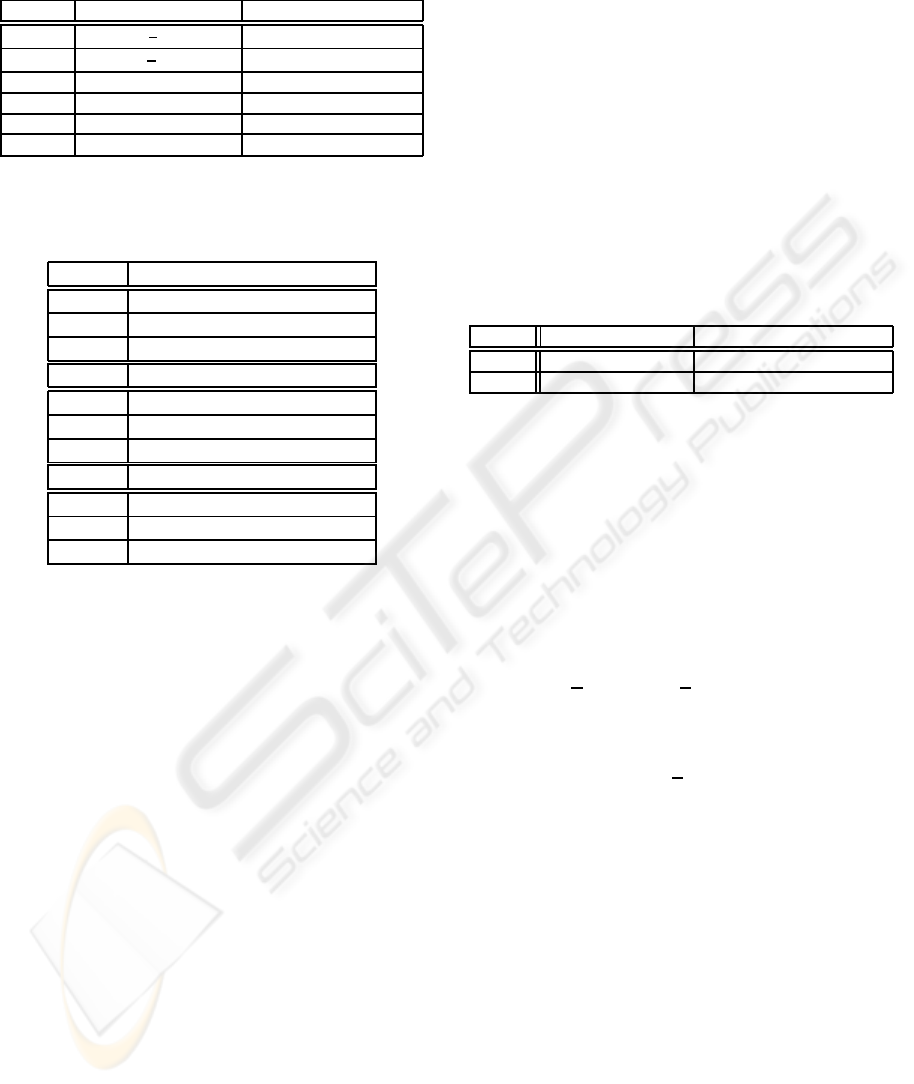
Table 1: Representations of the conformal geometric enti-

ties.

entity standard repr. direct repr.

Point P = x+

∞

+ e

Sphere s = P−

∞

∗

= x

∧ x

Plane π = n+de

∞

∗

= x

∧ x

∧ e

∞

Circle z = s

∧ s

∗

= x

∧ x

Line l = π

∧ π

∗

= x

∧ x

∧ e

∞

P-Pair P

= s

∧ s

∗

= x

∧ x

Table 2: The geometric meaning of the inner product of

conformal vectorsU (1st column) andV (2nd column, rows

1,5, and 9).

U ·V plane

plane angle between planes

sphere Euclidean distance to center

point Euclidean distance

U ·V sphere

plane Euclidean distance to center

sphere distance measure

point distance measure

U ·V point

plane Euclidean distance

sphere distance measure

point Euclidean distance

dard representation a sphere is represented with the

help of its center point P and its radius r, while in

the direct representation it is constructed by the outer

product ’∧’ of four points x

that lie on the surface of

the sphere (x

∧ x

). In standard representa-

tion the dual meaning of the outer product is the in-

tersection of geometric entities. For example a circle

is deﬁned by the intersection of two spheres (s

∧ s

Please notice that in this paper we indicate 3D vectors

by bold letters, e.g. n means the 3D normal vector of

a plane.

For the foundations of conformal geometric alge-

bra and its application to computer graphics refer for

instance to (L.Dorst et al., 2007), (Rosenhahn, 2003),

(Fontijne and Dorst, 2003) and to the tutorials (Dorst

and Mann, 2002), (Mann and Dorst, 2002), (Hilden-

brand et al., 2004) and (Hildenbrand, 2005).

3 DISTANCES AND ANGLES

In conformal geometric algebra distances and angles

are expressible easily with the help of the inner prod-

uct. Table 2 summarizes the geometric meaning of

the inner product of conformal vectors U and V.

The inner product of vectors in Conformal Geo-

metric Algebra results in a scalar and can be used as

a measure for distances between basic objects. The

inner product P· S of two vectors P and S can be used

for tasks like

• the Euclidean distance between two points

• the distance between one point and one plane

• the decision whether a point is inside or outside of

a sphere.

A vector in Conformal Geometric Algebra can be

written as

V = v

+ v

∞

+ v

(1)

The meaning of the two additional coordinates e

and

∞

is as follows :

= 0 v

6= 0

= 0 plane through origin sphere/point through origin

6= 0 plane sphere/point

The multiplication with a constant k 6= 0 leads al-

ways to the same geometric object (like in projective

space).

Division by v

6= 0 leads to (normalized form)

S = s

+ s

∞

+ e

(2)

representing a sphere S with center point s and ra-

dius r as

S = s+ s

∞

+ e

(3)

with

− r

) =

+ s

− r

)

Points are degenerate spheres with radius r = 0.

P = s+

∞

+ e

(4)

Planes are degenerate spheres with inﬁnite radius.

They are represented as a vector with v

= 0

V = v

+ v

∞

= v + v

∞

(5)

The inner product of 3D vectors corresponds to the

well-known scalar product. The 3D basis vectors

square to 1

= e

= 1 (6)

Because of the speciﬁc metric of the conformal space,

the additional basis vectors e

∞

square to 0 and their

inner product results in e

∞

· e

= −1 . Based on these

speciﬁc properties the inner product between a Con-

formal vector U and a Conformal vector V is deﬁned

U ·V = (u+ u

∞

+ u

) · (v+ v

∞

+ v

)

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

100

also expressible as

U ·V = u· v− u

− u

(7)

U ·V = u

+ u

− u

In the case of U and V both being points we get

U ·V = −

(s− p)

We recognize that the square of the Euclidean dis-

tance of the inhomogenous points corresponds to the

inner product of the homogenous points multiplied by

−2.

(s− p)

= −2(U ·V) (8)

For a vectorU representing a point and a vectorV rep-

resenting a plane with normal vector n and distance d

we get according to equation (7)

U ·V = P· π = p· n− d (9)

representing the Euclidean distance of the point and

the plane. Note that the scalar product p· n describes

the distance of the plane from the origin. Subtraction

of d results in the Euclidean plane to point distance.

For a vector U representing a plane with normal vec-

tor n and origin distance d and a vectorV representing

a sphere we get according to equation (7)

U ·V = π · S = n· s− d (10)

representing the Euclidean distance of the sphere cen-

ter from the plane.

For two vectors S

and S

representing two spheres

we get

2(S

· S

) = r

+ r

− (s

− s

)

(11)

This means that twice the inner product of two

spheres equals the sum of the square of the radii mi-

nus the square of the Euclidean distance of the sphere

centers.

We will see now that the inner product of a point

and a sphere can be used for the decision of whether

a point is inside or outside of a sphere. For a vector

P representing a point (sphere with radius 0) and a

vector S representing a sphere with radius r we get

according to equation (11)

2(P· S) = r

− (s− p)

(12)

That is equal to the square of the radius minus the

square of the distance between the point and the

center point of the sphere.

Based on this observation we can see that for

P· S > 0 : p is inside of the sphere

P· S = 0 : p is on the sphere

P· S < 0 : p is outside of the sphere

Angles between two objects o

like two lines

or two planes can be computed using the inner

product of the normalized direct representation of the

objects.

cos(θ) =

∗

· o

∗



∗



∗



(13)

θ = ∠(o

) = arccos

∗

· o

∗



∗



∗



(14)

Please refer to (Doran and Lasenby, 2003) for more

details.

Let us derive as one example an expression for the

angle between two planes based on the observation of

equation (7). For a vector π

representing a plane with

normal vector n

and distance d

we get

u = n

, u

= d

, u

= 0

For a vector π

representing another plane we get

v = n

, v

= d

, v

= 0

The inner product of the two planes is

· π

= n

· n

(15)

representing the scalar product of the two normals of

the planes.

Based on this observation the angle θ between two

planes can be computed as follows

cos(θ) = π

· π

(16)

This corresponds to equation (14) taking into account

that the planes are normalized and that the dualization

operation only switches between the two possible an-

gles between planes.

Please notice that the same is also true for two cir-

cles. In this case the inner product describes the co-

sine of the respective carrier planes of the two circles.

4 DIFFERENTIAL GEOMETRY

In order to analyze point clouds some properties of

conformal geometric algebra are very helpful. As-

suming some kind of curvature information of point

clouds the easy handling of geometric objects like cir-

cles and lines can be used for the local description of

curvature. Based on these local properties the exis-

tence of geometric objects like cylinder, sphere, cone

or torus can be investigated.

(Adamson, 2007) already developed algorithms to

estimate local curvature information including princi-

pal curvatures. These can be very easily be transferred

into algebraic expressions describing locally ﬁtting

objects. These objects include

ANALYSIS OF POINT CLOUDS - Using Conformal Geometric Algebra

101

• osculating circle (see ﬁgure 2)

• line describing vanishing curvature (see ﬁgure 3)

• osculating circle with vanishing radius (see ﬁg-

ure 1)

and can be treated very consistently in conformal geo-

metric algebra since all these objects have the same

algebraic structure. They are bivectors easy to com-

pute with.

Figure 1: Local coordinate system at point p

based on the

tangent vector t and the normal vector n.

Figure 2: Osculating circle describing the curvature at point

Circles can be described with the help of the outer

product of 3 points lying on the the circle or as the

intersection of a sphere and a plane resulting in the

following formula

Z = (c× n

123

− n

∧ e

− (c· n

∞

∧ e

+[(c· n

)c−

− r

] ∧ e

∞

Lines can be described with the help of the outer

product of 2 planes or as

L = ue

123

+ m∧ e

∞

(17)

Figure 3: Line describing vanishing curvature at point p

with u = b−a as Euclidean direction vector and m =

a × b as the moment vector. The corresponding six

Pl¨ucker coordinates are

(u : m) = (u

: u

: m

). (18)

Figure 4: Pl¨ucker parameters u and m of the line through a

and b.

5 FITTING OF POINTS WITH

THE HELP OF A SPHERE

While in (Hildenbrand, 2005) ﬁtting of spheres or

planes into point clouds is described, in this section

a point cloud p

∈ R

, i ∈ { 1,...,n} will be approxi-

mated speciﬁcally with the help of a sphere. The in-

homogenous points p

are represented as

= p

∞

+ e

(19)

and the sphere S with inhomogenous center point s

and radius r is represented according to equation (3).

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

102

5.1 Approach

In order to solve the approximation problem we

• deﬁne a distance measure between point and

sphere with the help of the inner product.

• make a least squares approach to minimize the

squares of the distances between the points and

the sphere.

• solve the resulting linear system of equations.

5.2 Distance Measure

According to section 3 the inner product between a

point P

and the sphere S

· S = (p

∞

+ e

) · (s+ s

∞

+ e

) (20)

can be used as a measure for their distance. This re-

sults in

· S = p

· s−

− s

according to equation (7) which can be written as

· S = w

i,1

+ w

i,2

+ w

i,3

+ w

i,4

+ w

i,5

· S =

∑

j=1

i, j

) + w

i,5

(21)

with

i,k







i,k

: k ∈ {1, 2,3}

−1 : k = 4

−

: k = 5

5.3 Least Squares Approach

In the least-squares sense we consider the minimum

of the squares of the distances between all the points

and the sphere

min

∑

i=1

· S)

(22)

In order to obtain the minimum we have the following

4 necessary conditions

∀k ∈ {1..4} :

∂(

∑

i=1

· S)

)

∂s

∑

i=1

∂(P

· S)

∂s

= 0

(23)

With the help of

∂(P

· S)

∂s

= 2(P

· S) ·

∂(P

· S)

∂s

and

∂(P

· S)

∂s

∂(

∑

j=1

i, j

) + w

i,5

)

∂s

= w

i,k

we obtain

∀k ∈ {1..4} :

∑

i=1

∂(P

· S)

∂s

= 2

∑

i=1

(

∑

j=1

i, j

i,k

) + w

i,5

i,k

) = 0

∀k ∈ {1..4} :

∑

i=1

∑

j=1

i, j

i,k

) = −

∑

i=1

i,5

i,k

)

which is the same as

∀k ∈ {1..4} :

∑

j=1

∑

i=1

i, j

i,k

) = −

∑

i=1

i,5

i,k

)

∀k ∈ {1..4} :

∑

j=1

∑

i=1

i, j

i,k

) = −

∑

i=1

i,5

i,k

)

leading to the following linear equation system







∑

i,1

∑

i,2

i,1

∑

i,3

i,1

∑

i,4

i,1

∑

i,1

i,2

∑

i,2

∑

i,3

i,2

∑

i,4

i,2

∑

i,1

i,3

∑

i,2

i,3

∑

i,3

∑

i,4

i,3

∑

i,1

i,4

∑

i,2

i,4

∑

i,3

i,4

∑

i,4







· s







−

∑

i,5

i,1

−

∑

i,5

i,2

−

∑

i,5

i,3

−

∑

i,5

i,4







For a ﬁtting sphere, the result of the least squares

approach is as follows :







∑

i,1

∑

i,2

i,1

∑

i,3

i,1

−

∑

i,1

∑

i,1

i,2

∑

i,2

∑

i,3

i,2

−

∑

i,2

∑

i,1

i,3

∑

i,2

i,3

∑

i,3

−

∑

i,3

−

∑

i,1

−

∑

i,2

−

∑

i,3

∑







· s







∑

i,1

∑

i,2

∑

i,3

−

∑







with p

i,1

, p

i,2

, p

i,3

as inhomogenous coordinatesof the

points p

. The result s = (s

) represents the

center point of the sphere (s

) and its radius in

terms of r

= s

+ s

− 2s

6 BOUNDING SPHERE

ALGORITHM

The problem of deﬁning a bounding sphere of a point

cloud can be subdivided into three sub-problems:

ANALYSIS OF POINT CLOUDS - Using Conformal Geometric Algebra

103

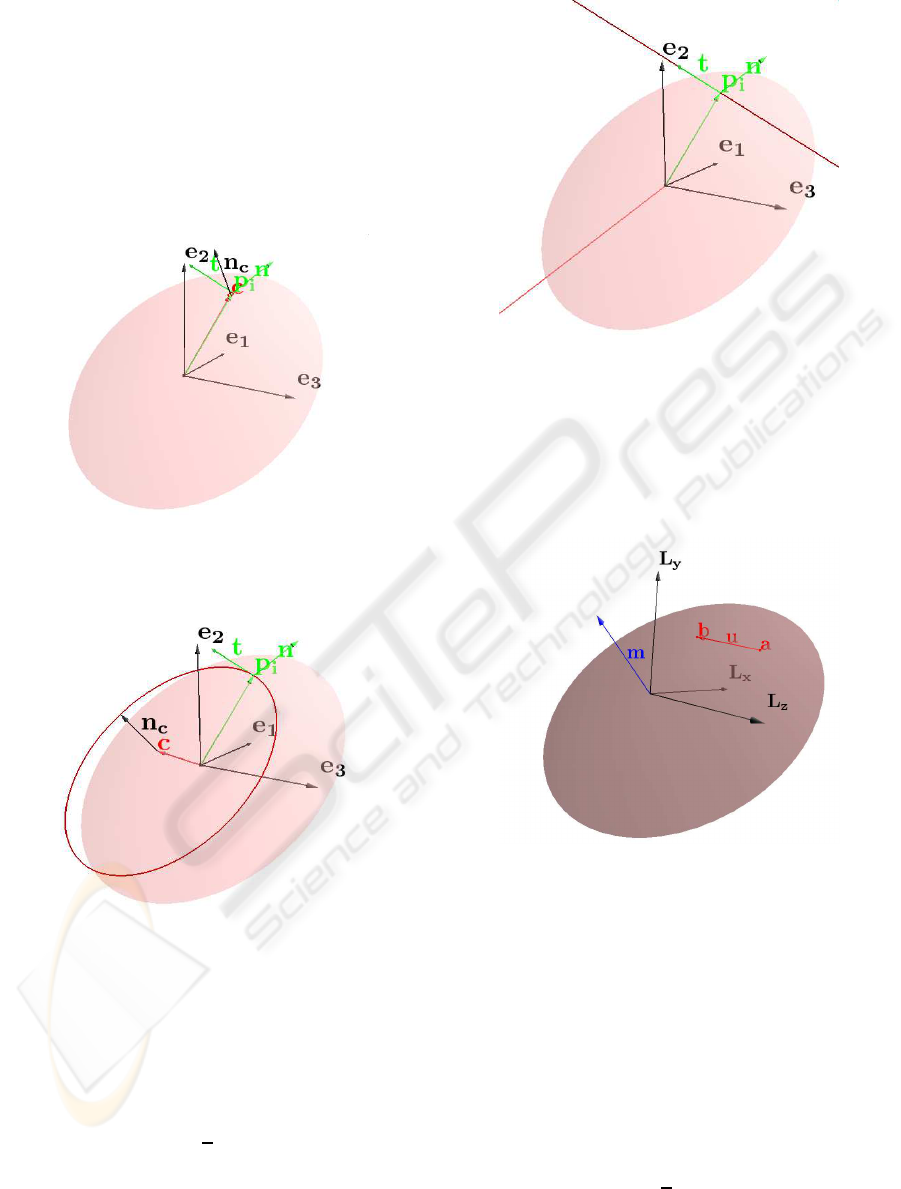
1. How to enclose a set of points by a minimal

sphere.

2. How to minimally expand an existing bounding

sphere when adding more points.

3. How to merge existing bounding spheres.

Because points can be treated as spheres of zero

radius, case 2 becomes part of case 3 if the latter is

solved for bounding sheres of general radii, including

the radius zero.

6.1 Point Clouds with One, Two or

Three Points

Conformal geometric algebra adds an origin-inﬁnity

plane to 3D Eucldean space. The origin-inﬁnity plane

is given by its bivector blade E = e

∞

∧ e

. The blade

E can be used to extract pure Euclidean parts from

conformal multivectors M

Euclid

= (M ∧ E) · E . (24)

We represent spheres by 5D vectors S in the

4,1

conformal model of three-dimensionalEuclidean

space. In general the conformal model uses blades A

for the socalled inner product null space representa-

tion (IPNS) of conformal subspaces V,

X · A

= 0 ⇔ X ∈ V, (25)

which is dual to the direct outer product null space

representation (OPNS)

X ∧A

∗

= 0 ⇔ X ∈ V, A

∗

= A

−1

= −A

123

(26)

Section 2 gave examples of blades A

for circles and

lines and Equ. (29) shows how to obtain a sphere

(blade) vector (A

= S).

If the cloud consists of only one point

P = p+

∞

+ e

, (27)

this point deﬁnes its own bounding sphere with con-

formal center C = P and radius zero r = 0.

If the cloud consists of two points,

= p

∞

+ e

, 1 ≤ k ≤ 2, (28)

the minimal bounding sphere has P

and P

as its

poles. The conformal sphere vector (see Fig. 5) is

then given by

S =

+ P

). (29)

The factor one half is convenient for keeping the

inner product of S with e

∞

S· e

∞

= −1. (30)

Figure 5: Sphere vector constructed from two pole points.

This is not necessary, because the conformal objects

are homogeneous, but helpful regarding numerical

implementations. We can always norm a sphere by

S →

−S· e

∞

(31)

and thus achieve (30). The radius of a normed sphere

is given by

= S

. (32)

The conformal center of a normed sphere is then given

C = S+

∞

. (33)

The Euclidean center vector of a sphere is given ac-

cording to (24) by

c = (C∧ E) · E. (34)

In the case of three conformal points

= p

∞

+ e

, 1 ≤ k ≤ 3, (35)

we can ﬁrst deﬁne an initial sphere with two points

(e.g. P

) as in Equ. (29). Then we can regard the

third point as a second sphere with zero radius and

center P

and apply the method for the bounding of

two spheres described in subsection 6.3. Or we can

directly expand the sphere to minimally include the

third point in the following way.

6.2 Minimally Including a New Point

We describe this alternative (compared to subsection

6.3) way in order to show that geometric algebra of-

fers a variety of algorithmic constructions, some of

which may be preferable for speciﬁc tasks and for nu-

merical optimization.

We show two variants in the form of CLUCalc

Scripts. The ﬁrst more from a geometric algebra prin-

ciple point of view, the second based on further code

performance optimization with Maple.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

104

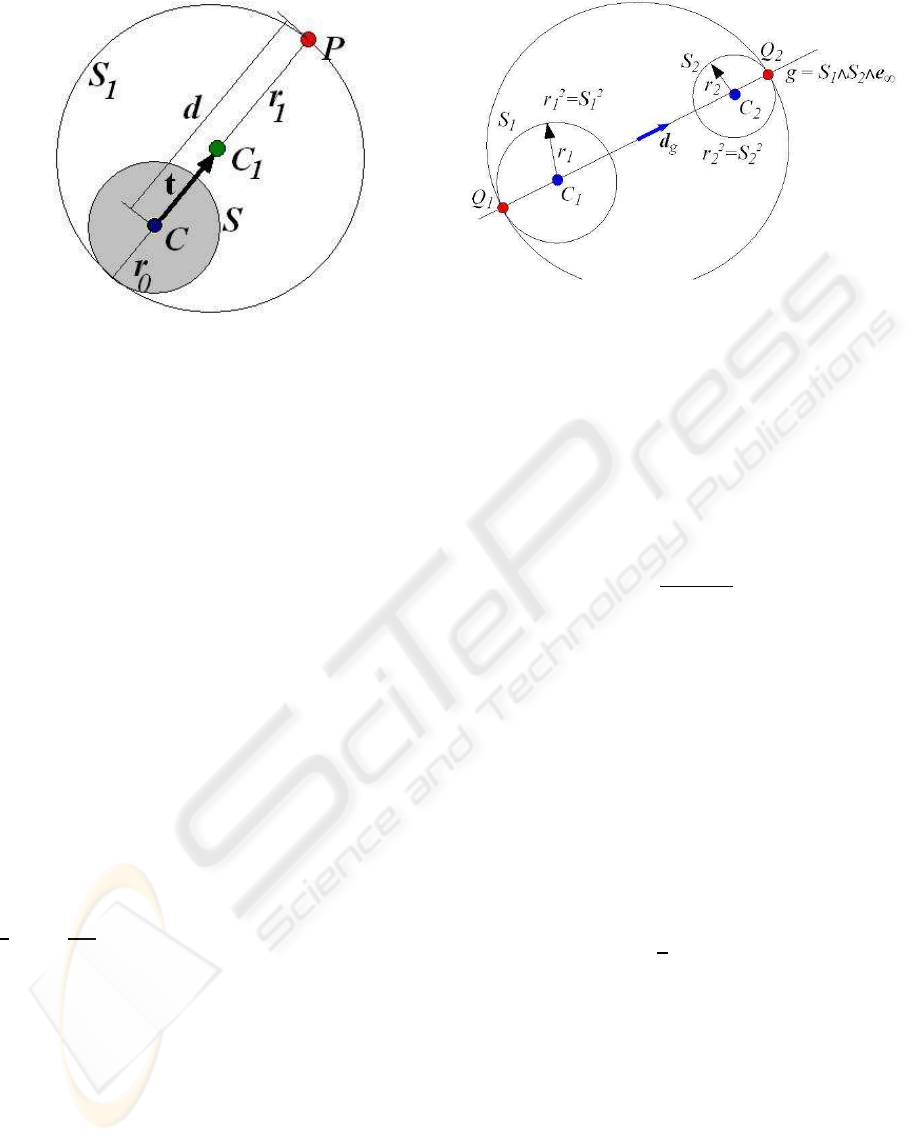
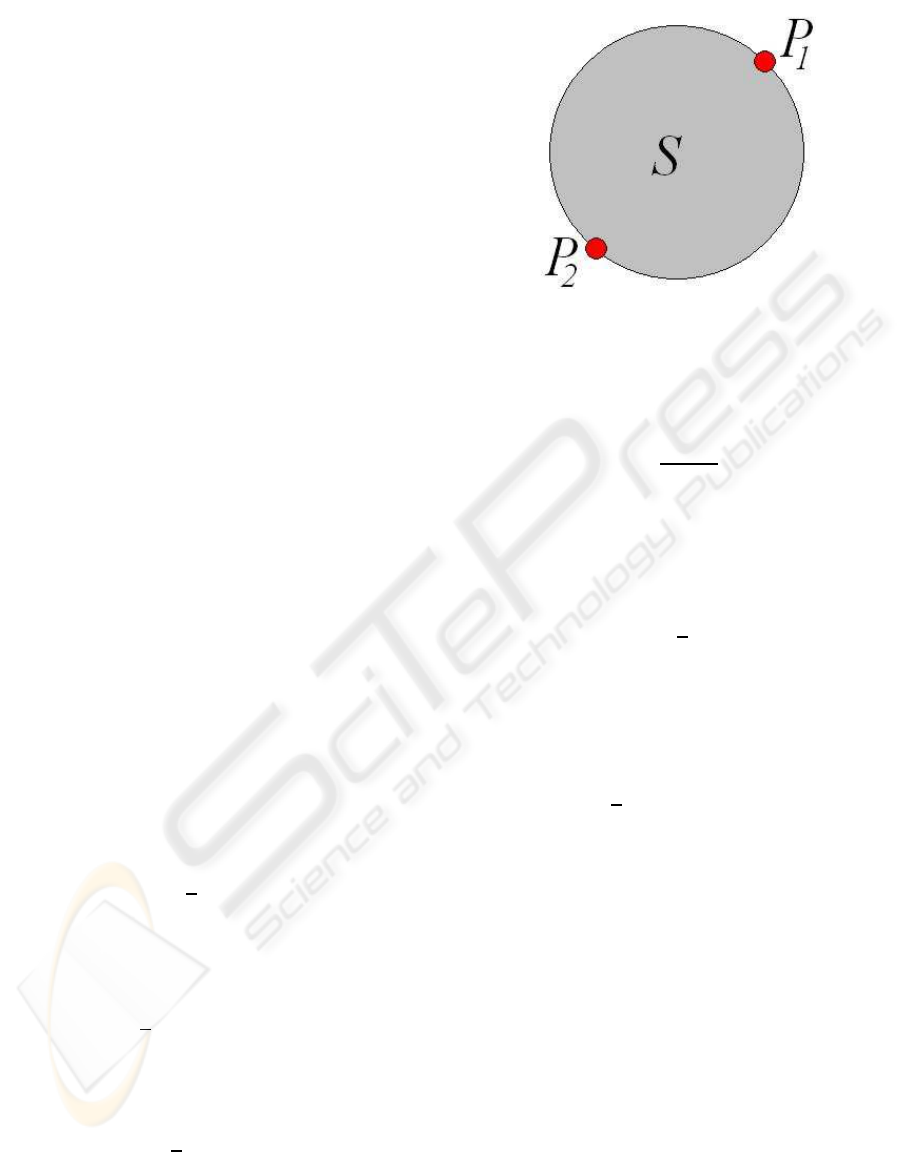
Figure 6: Minimally adding a point P to a sphere S by ad-

justing center and radius.

DefVarsN3(); // se of conformal model

:IPNS; // Use of inner product null space repr.

C = VecN3(c1,c2,c3); // Conformal sphere center

r=r0; // Sphere radius

S =C-0.5*r*r*einf;

//Definition of initial sphere S

P=VecN3(p1,p2,p3); // New point outside S

d = sqrt(-2*P.C);

//Distance between sphere center C and P

if (d>r){

CP = (p1-c1)*e1 + (p2-c2)*e2 + (p3-c3)*e3;

// Vector CP

T = 1 + 0.5* 0.5*(1-r/d)*CP *einf;

// Translator to new center

C1 = ˜T*C*T;

// Center of new sphere

r1 = (d+r)/2;

// Radius of new sphere

S1 = C1 - 0.5*r1*r1*einf;

// Def. of new sphere

}

We see in the CLUCalc Script that the sphere is

only expanded if the new point P is outside the sphere

S (d > r). C

is the center of the expanded sphere S

obtained by shifting C in the direction of P by t =

(d − r)

|CP|

, because d = |CP|. r

= (d + r)/2 is the

radius of the minimally expandedsphere S

. Compare

Fig. 6.

For numerical optimization we can replace the

deﬁnition of d and the if loop by Maple optimized

code

d=sqrt((p1-c1)*(p1-c1)+(p2-c2)*(p2-c2)+(p3-c3)*(p3-c3));

if (d>r){

c1x = (-r*p1+r*c1+p1*d+c1*d)/d/2;

c1y = ( r*c2+p2*d+c2*d-r*p2)/d/2;

c1z = ( p3*d-r*p3+r*c3+c3*d)/d/2;

r1 = (d+r)/2;

S1 = VecN3(c1x,c1y,c1z) - 0.5*r1*r1*einf;}

Figure 7: Minimal bounding sphere of two spheres.

6.3 Bounding Two Spheres

We can merge (bound) two spheres by deﬁning a

straight line g which connects the centers of the two

(normed) spheres S

and S

∗

= (S

∧ S

∧ e

∞

)

∗

. (36)

The Eulidean unit vector in the direction of g is then

d =

∗

· e

123

∗

· e

123

. (37)

We now calculate the poles of the minimal bounding

sphere. The ﬁrst pole is the point of intersection of g

with S

away from S

= c

− r

d, (38)

with c

and r

calculated according to (34) and (32).

We similarly obtain the second pole of the bounding

sphere as the point of intersection of g with S

away

from S

= c

+ r

d, (39)

The corresponding conformal poles (27) give accord-

ing to (29) the mininal bounding sphere (see Fig. 7)

+ Q

). (40)

In this section we developed the algebraic expres-

sions for the minimal bounding sphere [eqs. (36) to

(40)] for easy numerical implementation. It would be

possible to completely carry out the calculation of S

on the conformal level. For that purpose we would

ﬁrst calculate the conformal point pairs (OPNS) of in-

tersection of line g with sphere S

pair

= g · S

(41)

and of line g with sphere S

pair

= g · S

. (42)

ANALYSIS OF POINT CLOUDS - Using Conformal Geometric Algebra

105

With

pair

+ |pair

pair

· e

∞

(43)

and

pair

− |pair

pair

· e

∞

(44)

we can then directly pick the conformal points Q

and

out of the point pairs pair

and pair

If (like in subsection 6.2) the second sphere S

happens to be only a point (sphere with zero radius),

we can omit the calculation of Q

in Equs. (39), (42)

and (44). We simply replace Q

= S

in Equ. (40).

6.4 Comparison with Welzl’s Bounding

Sphere Algorithm

The iteration of the method suggested in subsection

6.3 (test of inclusion, and if necessary the calcula-

tion of the new bounding sphere) results in the ﬁnal

bounding sphere of n points in linear time O(n). The

proposed method is easy to understand and with given

routines for inner and outer products easy to imple-

ment. As demonstrated in subsection 6.2 the algo-

rithm can be further optimized with Maple. In aver-

age Welzl’s algorithm (Welzl, 1991) also runs in as-

ymptotically linear time, but the recursion in Welzl’s

algorithm makes it harder to examine and guarantee

the performance time.

7 CONCLUSIONS

We presented a bunch of basics and algorithms ex-

pressed in the mathematical framework of conformal

geometric algebra. We are convinced that its easy

handling of geometric objects like spheres, circles or

planes, its easy handling of distances and angles be-

tween them as well as its way of ﬁtting and bounding

of geometric objects will provide a promising foun-

dation for the analysis of point clouds.

REFERENCES

Adamson, A. (2007). Computing Curves and Surfaces from

Points. PhD thesis, Darmstadt University of Technol-

ogy.

Doran, C. and Lasenby, A. (2003). Geometric Algebra for

Physicists. Cambridge University Press.

Dorst, L. and Mann, S. (2002). Geometric algebra: a

computational framework for geometrical applica-

tions (part i: algebra). Computer Graphics and Ap-

plication, 22(3):24–31.

Fontijne, D. and Dorst, L. (2003). Modeling 3D euclid-

ean geometry. IEEE Computer Graphics and Appli-

cations, 23(2):68–78.

Hildenbrand, D. (2005). Geometric computing in computer

graphics using conformal geometric algebra. Comput-

ers & Graphics, 29(5):802–810.

Hildenbrand, D., Fontijne, D., Perwass, C., and Dorst, L.

(2004). Tutorial geometric algebra and its applica-

tion to computer graphics. In Eurographics confer-

ence Grenoble.

Hildenbrand, D., Fontijne, D., Wang, Y., Alexa, M., and

Dorst, L. (2006). Competitive runtime performance

for inverse kinematics algorithms using conformal

geometric algebra. In Eurographics conference Vi-

enna.

L.Dorst, Fontijne, D., Mann, S., and Kaufman, M. (2007).

Geometric Algebra for Computer Science, An Object-

Oriented Approach to Geometry. Morgan Kaufman.

Mann, S. and Dorst, L. (2002). Geometric algebra: a

computational framework for geometrical applica-

tions (part ii: applications). Computer Graphics and

Application, 22(4):58–67.

Rosenhahn, B. (2003). Pose Estimation Revisited. PhD

thesis, Inst. f. Informatik u. Prakt. Mathematik der

Christian-Albrechts-Universit¨at zu Kiel.

Schnabel, R., Wahl, R., and Klein, R. (2007). Efﬁcient

ransac for point-cloud shape detection. Computer

Graphics Forum, 26(2):214–226.

Welzl, E. (1991). Smallest enclosing disks (balls and ellip-

soids. In Lecture Notes in Computer Science, pages

555:359–370.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

106