
EFFICIENT FACE-BASED NON-SPLIT CONNECTIVITY
COMPRESSION FOR QUAD AND TRIANGLE-QUAD MESHES
D. R. Khattab, Y. M. Abd El-Latif, M. S. Abdel Wahab and M. F. Tolba
Faculty of Computers and Information Sciences, Ain Shams University, Abbassia, 11566, Cairo, Egypt
Keywords: Non-triangular mesh compression, Non-split encoding, Connectivity compression.
Abstract: In this paper we present an efficient face-based connectivity coding technique for the special class of
quadrilateral and the hybrid triangular-quadrilateral meshes. This work extends the main ideas of non-split
encoding presented by the first contribution of the authors (Khattab, Abd El-Latif, Abdel Wahab and Tolba,
2007) for triangle meshes and improves over the compression results provided so far for existing face-based
connectivity compression techniques. It achieves an average compression ratio of 2.17 bits per quad and per
vertex for simple quadrilateral meshes and bit rates of 1.84 bits per polygon and 1.85 bits per vertex for the
simple hybrid triangle-quad meshes.
1 INTRODUCTION
While a picture is often said to be worth a thousand
words, a 3D model could be said to be worth a
thousand pictures. Polygonal meshes are used most
often as surface representation because of their wide
spread support in many file formats and graphic
libraries. These large and complex meshes are
becoming commonplace because of the increasing
capabilities of the computing environments,
visualization hardware, modern interactive
modelling tools and semi automatic 3D data
acquisition systems. The complexity of these models
poses basic problems of efficient storage in file
servers, transmission over computer networks,
rendering, analysis, processing etc. Therefore,
efficient 3D mesh compression algorithms have
been in high demand in the past few years to reduce
the storage room needed for large, detailed 3D
models and to consequently decrease transmission
time over a network.
Much of the work done in the area of single-
rate mesh connectivity compression has focused on
triangle meshes only (Deering, 1995, Chow, 1997,
Gumhold and Strasser 1998, Rossignac, 1999,
Touma and Gotsman, 1998 and Alliez and Desbrun
2001). However there are a significant number of
non-triangular meshes in use. These models contain
a surprisingly small percentage of triangles likewise;
few triangles are generated by tessellation routines
in existing modelling software. The dominant
element in these meshes is the quadrilateral, but
pentagons, hexagons and higher degree faces are
also common (Alliez and Gotsman, 2005). The
extension of the previously mentioned algorithms to
deal with non-triangular meshes is not obvious.
Hence, in practice, non-triangular meshes are coded
by triangulating them, coding the results using one
of the methods of coding triangular meshes and
storing additional information describing the extra
edges introduced during the triangulation stage.
These edges are discarded after decoding to restore
the original polygonal model. This means that the
code of a non-triangular mesh might be larger than
that of the triangular version, instead of being
shorter, as less connectivity information is present.
In addition, it is beneficial for storage purposes
to keep a mesh in its native polygonal representation
than to triangulate it. This is because most meshes
have associated properties such as normal, colour, or
texture information that account for a large portion
of the storage cost. Triangulating a polygon mesh
not only adds an extra processing step, but also
increases the number of faces and corners and
replicates their associated properties.
1.1 Related Work
To address the problem of compressing the
connectivity of non-triangular meshes, several
algorithms have been proposed to encode polygonal
meshes directly without pre-triangulation. In this
31
R. Khattab D., M. Abd El-Latif Y., S. Abdel Wahab M. and F. Tolba M. (2008).
EFFICIENT FACE-BASED NON-SPLIT CONNECTIVITY COMPRESSION FOR QUAD AND TRIANGLE-QUAD MESHES.
In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 31-38
DOI: 10.5220/0001093900310038
Copyright
c
SciTePress

section we focus on recent coding methods for
manifold meshes that grow a region over the mesh
and incrementally encode the mesh elements and
their incidence relations to the growing region. The
methods are categorized as face-based, edge-based
and vertex-based methods according to the type of
mesh element playing the dominant role in the
compression scheme.
King et al. (King, Rossignac and Szymczak,
1999) first proposed a connectivity coding algorithm
for quad or mixed triangle-quad meshes, by
generalizing the EdgeBreaker algorithm (Rossignac,
1999 and Rossignac and Szymczak, 1999) which is
one of the triangle conquest methods. This method
implicitly triangulates each quadrilateral to two
triangles and uses sequences of the five basic
EdgeBreaker labels (CLERS) to code the different
possibilities which then arise. This introduced a
compressed format based on entropy coding with a
worst case of 2.67 b/v. Isenburg and Snoeyink
(Isenburg and Snoeyink, 2000) proposed an edge-
based technique called the Face-Fixer. They
achieved a connectivity coding cost of 5 b/v for
simple triangular meshes and 4 b/v for simple
quadrilateral meshes.
Isenburg (Isenburg, 2002) and Khodakovsky et
al. (Khodakovsky, Alliez, Desbrun and Schröder,
2002) independently proposed similar vertex-based
algorithms to encode the connectivity of a manifold
polygonal mesh. Their algorithms are extensions of
the valence-driven approaches (Touma and
Gotsman, 1998 and Alliez and Desbrun 2001).
Isenburg’s algorithm provides slightly better
compression performance than Khodakovsky et
al.’s. They both produce better results compared to
the Face-Fixer. Another vertex-based technique is
the Angle-Analyzer (Lee, Alliez and Desbrun,
2002). The algorithm focused on the hybrid triangle-
quad mesh coding. On average, the algorithm yields
40% and 20% better compression ratios for
connectivity and geometry data than the state-of-the-
art triangular mesh coder given in (Touma and
Gotsman, 1998).
As a face-based technique, Kronrod and
Gotsman (Kronrod and Gotsman, 2000) introduced a
general and direct technique for coding the
connectivity of any non-triangular mesh with an
upper bound on the resulting code length. The
algorithm generalizes EdgeBreaker technique
(Rossignac, 1999) for non-triangular meshes. They
proved that for quadrilateral meshes a worst case of
3.5 bits per quad and per vertex can be achieved and
a worst case of 4 bits per polygon can be achieved
for quad meshes with few triangles.
Two enhancements over the bit rates of
Kronrod and Gotsman algorithm were introduced.
The enhanced technique of (Mukhopadhyay and
Jing, 2003) proved with complex calculations that
the bit rates can be reduced to less than 3 b/v. and by
equivalence to the work done in (King, Rossignac
and Szymczak, 1999) can be reduced to 2.67 b/v. the
other enhancement (Kosicki and Mukhopadhyay,
2004) improved the results to 2.4 b/v using
arithmetic coding.
1.2 Overview
In this paper we introduce an efficient face-based
connectivity coding technique that extends the ideas
of non-split coding presented by the authors’ first
contribution (Khattab, Abd El-Latif, Abdel Wahab
and Tolba, 2007) for triangle meshes. The
compression results achieved is the best compared to
the state-of-the-art face-based techniques for
compressing non-triangular meshes. These results
are compared to those introduced by Kronrod and
Gotsman (Kronrod and Gotsman, 2000) and their
enhancements of (Mukhopadhyay and Jing, 2003
and Kosicki and Mukhopadhyay, 2004).
The remainder of this paper is organized as
follows: section 2 explains the encoding scheme of
Kronrod and Gotsman. Section 3 illustrates the
proposed technique for applying the non-split
encoding to non-triangular meshes. The results and
discussions are presented in section 4 and we
conclude in section 5.
2 KRONROD-GOTSMAN
SCHEME
The Kronrod-Gotsman scheme (Kronrod and
Gotsman, 2000) generalizes the CLRES labelling
scheme of EdgeBreaker (Rossignac, 1999) to non-
triangular meshes. Their main observation is that as
we traverse a mesh in depth-first order, the
interaction of each polygon with the rest of the mesh
can be enumerated in a finite number of ways. For
example, in a quad mesh each quad interacts with
the rest of the mesh in one of thirteen types labelled
from Q
1
to Q
13
(figure 1) and hence this interaction
can be coded in a unique manner. It is easy to
enumerate all these interaction types if we note that
each of the remaining three edges of the current
quad either belongs to the mesh boundary or does
not, and so also for the remaining two vertices.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
32
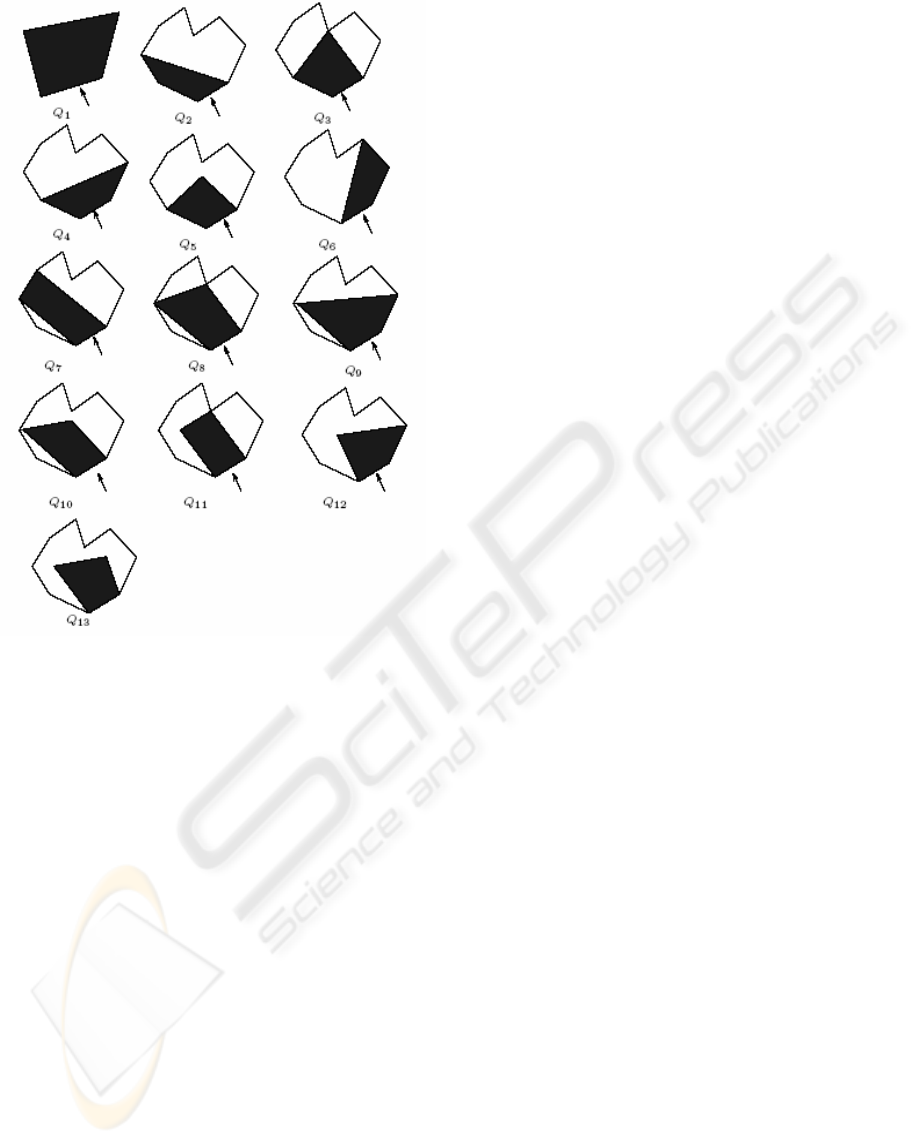
Figure 1: Interaction of a quad with the mesh. Arrows
indicate the current gate.
The compression process traverses the mesh in
depth- first order starting with a quad. It then records
a code of the interaction type of the current quad
with the boundary. After the quad is removed from
the boundary, the boundary is updated and the
procedure repeats. If the interaction type of the
removed quad contains gaps (i.e., the quad has at
least one touching vertex with the boundary) the
boundary will split into two or more boundaries. The
boundary is not stored explicitly; otherwise it is
maintained implicitly as a stack of gate edges. The
procedure terminates when the entire mesh is
reduced to nothing. The output of the encoder is
sufficient to reconstruct the connectivity data of the
mesh. The time complexity of the encoding
procedure is linear in the size of the mesh.
The decoding algorithm is inspired by the linear
time Spirale Reversi decoder (Isenburg and
Snoeyink, 2001). The algorithm is simple however;
it processes the mesh in the reverse order of the
encoding process. It means that mesh polygons will
be reconstructed in an order opposite to which they
were encoded. In the encoding process each
interaction type defines exactly how this polygon is
connected to all generated borders. Hence, if the
decoder knows the connectivity in the interior of the
boundary after the encoding step and the nature of
the interaction between the encoded polygon and the
active boundary, it is easy to reconstruct the
connectivity of the interior of the active boundary as
it was before the encoding step.
The authors provided explicit codes for the
interaction types of pure quad mesh and a quad mesh
with minority of triangles. For the case of a mesh
containing only quads it admits thirteen different
interaction types, which requires (log
2
13) = 4
bits/quad when coded using a fixed-length code. But
as not all the interactions occur with equal
frequencies they produced a more efficient variable-
length prefix code which reduced the total code
length to less than 3.5 bits/quad. For the case of
hybrid quad and triangle mesh, it admits eighteen
different interaction types, which are the summation
of the thirteen interaction types of pure quad meshes
and the five interaction types of triangular meshes
generated by EdgeBreaker (Rossignac, 1999). Again
the naïve coding will require (log
2
18) = 5 bits/quad
but using the same variable-length prefix code it was
reduced to less than 4 bits/poly.
3 NON-SPLIT ENCODING
The new encoding scheme presented in this paper
adapts the main idea of not splitting the boundary
while traversing the mesh. This idea was first
presented by the authors in their first contribution by
introducing an enhanced encoding technique for
triangle meshes (Khattab, Abd El-Latif, Abdel
Wahab and Tolba, 2007). This technique had
updated the CLERS string generated by
EdgeBreaker (Rossignac, 1999) to the CLRGF
string. This was done by the elimination of S
interaction type that causes the active boundary to be
split and so the elimination of its delimiter E label.
These two labels were replaced by another two
labels G and F for moving on the active boundary to
the left or the right of the current active gate. This
choice was decided according to which boundary
length is shorter. The next subsections explain how
this idea can be extended for encoding quadrilateral
and hybrid triangular-quadrilateral meshes.
3.1 Encoding Quadrilateral Meshes
For applying this technique on quad meshes, the
algorithm tends to eliminate the six interaction types
EFFICIENT FACE-BASED NON-SPLIT CONNECTIVITY COMPRESSION FOR QUAD AND TRIANGLE-QUAD
MESHES
33
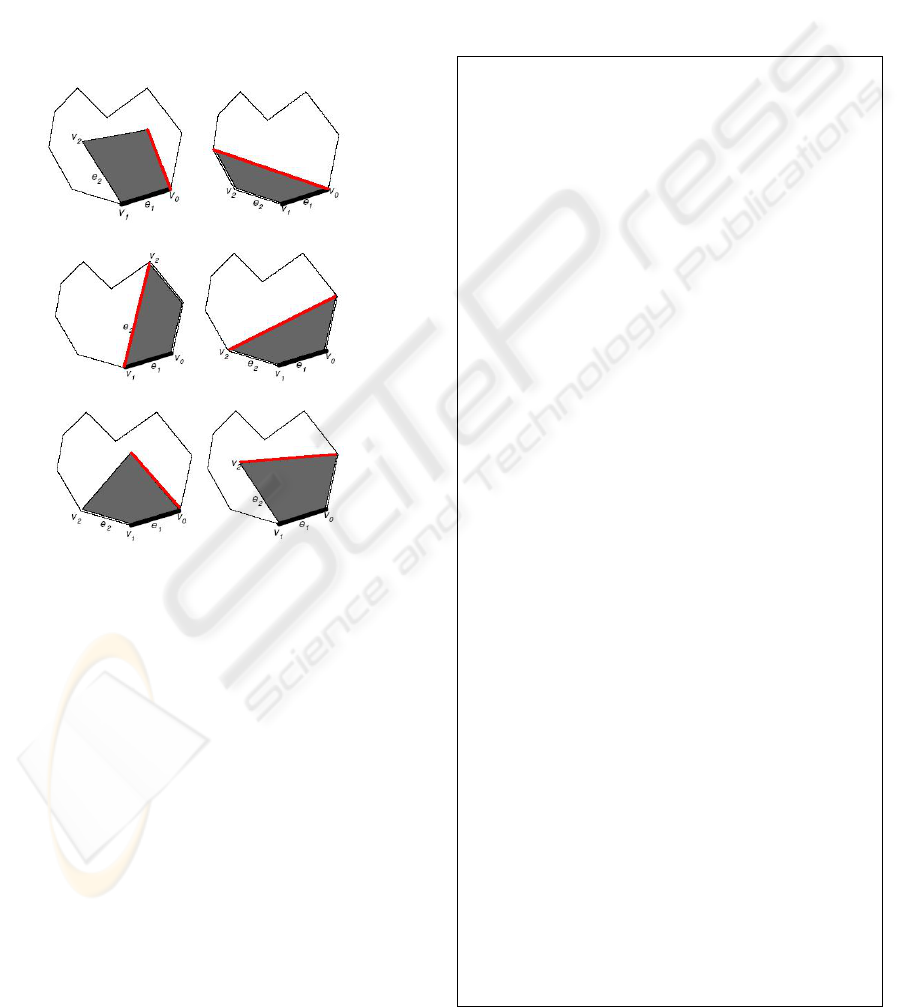
(Q
3
Q
7
Q
8
Q
9
Q
10
Q
11
) that cause the boundary to be
split from the thirteen interaction types defined by
Kronrod and Gotsman (figure 1). This ensures that
the active boundary will never split. The interaction
type of Q
1
which defines the state of the last reached
quad for every generated boundary after splitting
will never occur except only once at the end of mesh
traversal and so it can be replaced by the label Q
4
.
By this way the enhanced technique preserves only
six interaction types from the whole group of
thirteen interaction types defined by Kronrod and
Gotsman. These six interaction types are reordered
again from Q
1
to Q
6
as can be seen in figure 2.
Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
Figure 2: Remaining six interaction types of quad
interaction with a mesh. Thick black edges show the
current active gates. Thick red edges show the updated
active gates for each interaction type.
The eliminated labels are replaced with G and F
labels which indicate moving on the active boundary
wherever a split case occurs. The encoding string is
now changed to Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
GF. The elimination
of the split casess from encoding string saves for the
encoding technique many advantages. The algorithm
needs only to maintain one circular linked list for
active boundary during compression and
decompression. It also has eliminated both the
recursive overhead and computational overhead
needed by the stack to keep list of new active gates
generated after splitting. The decompression
processes is done in only one forward pass of
traversing the encoding string and reconstructs the
mesh quads in the same order they were encoded.
The pseudo-code of the proposed encoding
procedure is provided in the frame below. After
processing of each quad element, the active gate is
updated to the first edge incident to an unprocessed
element in the counter clock wise direction from the
current active gate. This can be observed by the red
edges shown in figure 2. This approach of updating
the active gate allows the traversal to be done in a
spiralling depth first clock wise order around the
mesh faces.
Input:
Geometry of the mesh as an array of floats to
specify positions.
Connectivity of the mesh as an array of integers
containing indices into the position array to
specify the faces.
Output:
Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
GF string that contains one
label per quad except for the first one.
Procedure compress_quad()
Assign flag to true
While (flag)
If both tip vertices are not visited Then
Append code of Q
1
to the encoding string,
Add both tip vertices to the list of vertices,
Mark quad and tip vertices as visited,
Update active gate.
Else If both tip vertices lies on the boundary
to the left of current active gate Then
Append code of Q
2
to the encoding string,
Mark quad as visited,
Update active gate.
Else If tip vertices lies on the boundary to
the right of current active gate Then
Append code of Q
3
to the encoding string,
Mark quad as visited,
Update active gate.
Else If first tip vertex lies on the boundary
to the left and second vertex lies to the right
of the active gate Then
Append code of Q
4
to the encoding string,
Mark quad as visited,
Update active gate.
Else If first tip vertex lies on the boundary
to the left of active gate and second tip
vertex is not visited Then
Append code of Q
5
to the encoding string,
Mark quad and second tip vertex as
visited,
Add second tip vertex to the list of
vertices,
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
34

Update active gate.
Else If first tip vertex is not visited and
second tip vertex lies on the boundary to the
right of active gate Then
Append code of Q
6
to the encoding string,
Mark quad and first tip vertex as visited,
Add first tip vertex to the list of vertices,
Update active gate.
Else
Calculate right and left boundary lengths
If the right boundary is shorter in length
Then
Append encoding of G to the
encoding string,
Update active gate to the next right
edge on the boundary.
Else If the left boundary is shorter in
length Then
Append encoding of F to the
encoding string,
Update active gate to the next left
edge on the boundary
If all mesh quads are processed then
Assign flag to false
3.2 Encoding Hybrid
Triangular-Quadrilateral Meshes
The only requirement needed in order to extend the
technique for triangle-quad meshes is to generalize
the data structure used by the encoding procedure to
be able to store elements with arbitrary number of
edges. The procedure checks for the current element
type either it is a triangle or a quad. This checking
distinct between two different subroutines
responsible for checking the different cases of each
type of elements and assigns the appropriate code
for each element.
The generated encoding string will be a mixture
of the six interaction types (Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
) for
encoding quad elements and the three interaction
types of (CRL) for encoding triangle elements. By
addition of the two labels of F and G, the generated
encoding string becomes Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
CLRGF.
The general layout of the procedure is explained in
the frame below.
Input:
Geometry of the mesh as an array of floats to
specify positions
Connectivity of the mesh as an array of
integers containing indices into the position
array to specify the faces.
Output:
Q
1
Q
2
Q
3
Q
4
Q
5
Q
6
CLRGF string that contains
one label per polygon except for the first one.
Procedure Compress()
Assign flag to true
While (flag)
If the current processed polygon is a triangle
then
Call procedure compress_triangle()
Else if the current processed polygon is a quad
then
Call procedure compress_quad()
If all mesh polygons are processed then
Assign flag to false
4 RESULTS AND DISCUSSION
In this section the compression ratio achieved using
the adapted non-split encoding technique is
evaluated. Sample test cases of pure quad meshes
(figure 3) and of quad meshes with few triangles
(figure 4) were collected for this purpose and
presented in Table 1. The meshes were selected to
have a variety in size and shape except they all share
the common characteristics of being manifold and
simple without boundary, holes or handles.
Table 1: Used benchmark 3D models.
Model
name
File size
No of
Quads
No of
triangles
No of
vertices
Cow 1.35 MB 25,878 - 25,880
Bumpy
sphere
1.41 MB 34,332 - 34,334
Egea 2.43 MB 49,596 - 49,598
Fandisk 3.55 MB 71,892 - 71,894
Head 4.94 MB 98,232 - 98,234
Horse 6.58 MB 119,09 - 119,096
Dente 6.95 MB 131,67 - 131,672
Eros 8.07 MB 153,91 - 153,914
Bimba 849 KB 15,532 238 15,653
Dragon 7.48 MB 126,77 1,540 127,571
EFFICIENT FACE-BASED NON-SPLIT CONNECTIVITY COMPRESSION FOR QUAD AND TRIANGLE-QUAD
MESHES
35

Cow Bumpy sphere
Egea Fandisk
Head Horse
Dente Eros
Figure 3: Benchmark 3D models of Quad meshes.
Bimba Dragon
Figure 4: Benchmark 3D models of Quad meshes with
few triangles.
In order for the compression ratio to be
calculated a binary code has to be given to each of
the encoding labels used for the encoding process.
Following the fact that not all the codes occur with
equal frequencies (Kronrod and Gotsman, 2000), a
study over the average percentage each label
consumes from the Encoding file was generated
(Khattab, Abd El-Latif, Abdel Wahab and Tolba,
2007) to the entire models used (figure 5).
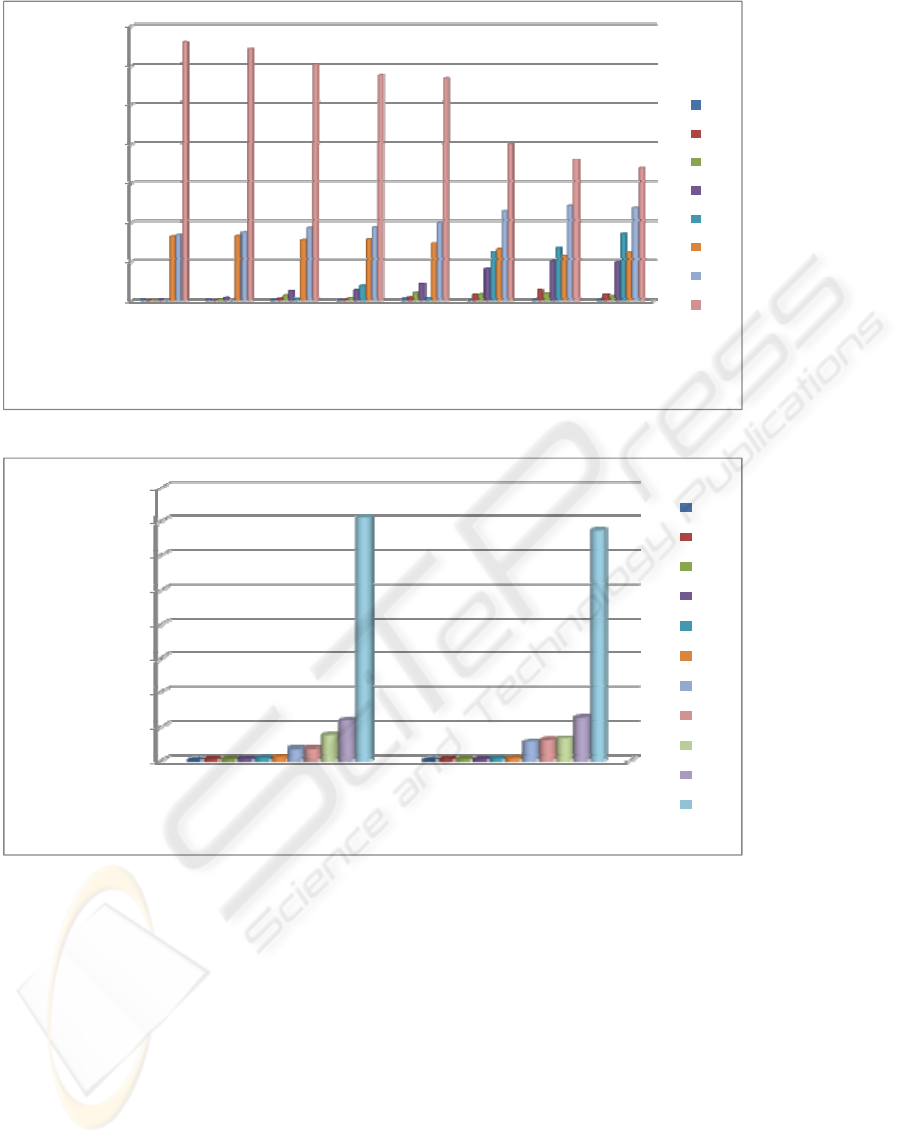
Figure 5 shows the frequency of occurrence of
each encoding label in all meshes and the average
percentage of each label over the whole group of
meshes. The encoding labels are arranged in an
ascending order according to their average
percentage of occurrence. It is apparent from figure
5a that the largest percentages of quad interaction
types are Q
6
, Q
1
and Q
3
respectively. This result
reflects the behaviour of the encoding technique that
emphasis on traversing the mesh in a spiralling clock
wise order of polygons. The same result is obtained
with triangle-quad meshes (figure 5b) again the label
R has the largest percentage among the set of
triangle labels (C, R and L).
Based on this study a variable length binary
code is given for the labels (Q
6
: 0, Q
1
: 10, Q
3
: 110,
F: 1110, Q
4
: 11110, Q
5
: 111110, Q
2
: 1111110, G:
1111111) of quad meshes and (Q
6
: 0, Q
1
: 10, Q
3
:
110, F: 1110, Q
4
: 11110, R: 111110, Q
2
: 1111110,
Q
5
: 11111110, G: 1111111110, C: 1111111110, L:
1111111111) of tri-quad meshes. This code is based
on Huffman coding (Huffman, 1952) and leads to
the optimal compression ratio that can be achieved.
Table 2: Compression results of quad meshes.
Connectivity size
Compression
ratio
File
name
Unencoded Encoded bpq bpv
Head 2.49 MB 18.44 KB 1.53 1.53
Fandisk 1.81 KB 13.92 KB 1.58 1.58
Bumpy
sphere
866 KB 7.3 KB 1.74 1.74
Dente 3.51 MB 30 KB 1.86 1.86
Egea 1.23 KB 11.58 KB 1.9 1.9
Eros 4.16 MB 50.94 KB 2.7 2.7
Horse 3.13 MB 42.93 KB 2.9 2.9
Cow 643 KB 9.8 KB 3.1 3.1
Average 2.17 2.17
Table 3: Compression results of triangle-quad meshes.
Connectivity size
Compression
ratio
File
name
Unencoded Encoded bpp bpv
Bimba 386 KB 511 KB 1.76 1.77
Dragon 3.35 MB 3.741 KB 1.92 1.93
Average 1.84 1.85
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
36
Average
Percentage
0.00%
10.00%
20.00%
30.00%
40.00%
50.00%
60.00%
70.00%
Head Fandisk Bumpy
sphere
Dente Egea Eros Horse Cow
Per cent sge %
Mesh Name
G
Q2
Q5
Q4
F
Q3
Q1
Q6
(a)
0.26%
1.00%
1.21%
4.9%
5.99%
14.6%
20.36%
51.81%
0.00%
10.00%
20.00%
30.00%
40.00%
50.00%
60.00%
70.00%
80.00%
Bi mba Dr ago n
Per cent age %
Mesh Name
L
C
G
Q5
Q2
R
Q4
F
Q3
Q1
Q6
(b)
0.06%
0.36%
0.38%
0.41%
0.67%
0.86%
4.27%
4.63%
6.93%
12.15%
69.28%
Figure 5: Frequency percentage each file consumes from the encoding data file.
Table 2 and 3 list the results of the bit rates of
compression ratio per polygon (bpp) and per vertex
(bpv) for quad meshes and the hybrid triangle-quad
meshes respectively. The results in both tables are
arranged in ascending order according to the
compression ratio which varies from the smallest bit
rate of 1.53 (Head example) to the largest bit rate of
3.1 (Cow example) for quad meshes.
This variation in results can be estimated by
referring to figure 5a which shows the degradation
in the percentage of Q
6
labels whose bit code length
is the least. This degradation is consumed in other
labels having larger bit code lengths. Another
parameter that affects the compression ratio is the
shape characteristics of the models (Khattab, Abd
El-Latif, Abdel Wahab and Tolba, 2007). The
largest percentage of split cases during mesh
traversal, the largest percentage of F and G labels
added to the encoding file which finally results in
much increase of bit rates per polygon for these
meshes.
According to the binary code associated to each
label, an average compression ratio of 2.17 bit per
quad and per vertex is achieved for quad meshes and
1.84 bit per polygon and 1.85 bit per vertex for
triangle-quad meshes. This result is more efficient
EFFICIENT FACE-BASED NON-SPLIT CONNECTIVITY COMPRESSION FOR QUAD AND TRIANGLE-QUAD
MESHES
37

compared to the late results obtained by Kronrod
and Gotsman (Kronrod and Gotsman, 2000) and its
enhancements of (Mukhopadhyay and Jing, 2003
and Kosicki and Mukhopadhyay, 2004) directly and
without applying any complex or arithmetic coding.
5 CONCLUSIONS
In this paper, we present an efficient face-based
connectivity encoding technique for compressing
non-triangular meshes. The presented technique
extends the previous work done by the authors in
their first contribution (Khattab, Abd El-Latif, Abdel
Wahab and Tolba, 2007) for compressing triangular
meshes to the special class of pure quad and hybrid
triangle-quad meshes. The presented technique
reduced the interaction types introduced by Kronrod
and Gotsman (Kronrod and Gotsman, 2000) from
thirteen to six by elimination of the interaction types
that causes the boundary to be split. This approach
saves for the encoding technique its simplicity and
efficiency. This reduction of interaction types
improved the compression ratio over the state-of-
the-art face-based techniques for compressing non-
triangular meshes. It is believed that applying
entropy or arithmetic coding to the achieved results
will lead to further increase in compression ratio.
The future work is to apply this efficient non-split
encoding technique for meshes with arbitrary
topology such as boundary and holes. The work in
this direction is under progress and the initial results
are promising.
REFERENCES
Alliez, P., Desbrun, M., 2001. Valence-driven
connectivity encoding of 3D meshes. In Proceeding of
Eurographies 2001 Conference, 480-489.
Alliez, P., Gotsman, C., 2005. Recent advances in
compression of 3D meshes. In Advances in
Multiresolution for Geometric, Springer-Verlag, 3-26.
Chow, M., 1997. Optimized geometry compression for
real-time rendering. In Proceedings of the 8th
conference on IEEE Visualization '97, Phoenix,
Arizona, United States, 347 – ff.
Deering, M., 1995. Geometry compression. In
Proceedings of the 22nd annual conference on
Computer graphics and interactive techniques,
SIGGRAPH, ACM, 13 - 20.
Gumhold, S., Strasser, W., 1998. Real time compression
of triangle mesh connectivity. In Proceeding of 25th
Annual Conference on Computer Graphics, 133-140.
Huffman, A., 1952. A method for the construction of
minimum-redundancy codes. Proc. Inst. Radio Eng.,
1098-1101.
Isenburg, M., 2002. Compressing polygon mesh
connectivity with degree duality prediction. In
Proceedings of Graphics Interface 02 Conference,
161-170.
Isenburg, M., Snoeyink, J., 2000. Face fixer: compressing
polygon meshes with properties. In Proceedings of the
27th annual conference on Computer graphics and
interactive techniques. SIGGRAPH, ACM, 263 – 270.
Isenburg, M., Snoeyink, J., 2001. Spirale Reversi: Reverse
decoding of the EdgeBreaker encoding.
Computational Geometry, vol. 20, no. 1, 39-52.
Khattab, D., Abd El-Latif. Y., Abdel Wahab. M., Tolba.
M., 2007. An enhanced EdgeBreaker compression
algorithm for the connectivity of triangular meshes. In
Proceedings of GRAPP Second International
Conference on Computer Graphics Theory and
Applications, Barcelona, Spain, 109 -115.
Khodakovsky, A., Alliez, P., Desbrun, M., Schröder. P.,
2002. Near-optimal connectivity encoding of 2-
manifold polygon meshes. 147-168.
King, D., Rossignac, J., Szymczak, A., 1999. Connectivity
compression of irregular quadrilateral meshes. Tech.
Rep. TR-99-36, GVU, Georgia Tec.
Kosicki. P., Mukhopadhyay. A., 2004. Encoding
Quadrilateral Meshes in 2.40 bits per Vertex. In
Proceedings of ICVGIP 2004, 89 – 94.
Kronrod. B., Gotsman. C., 2000. Efficient Coding of Non-
Triangular Mesh Connectivity. In Proceedings of the
8th Pacific Conference on Computer Graphics and
Applications, IEEE Computer Society, Washington,
DC, 235.
Lee. H., Alliez, P., Desbrun, M., 2002. Angle-Analyzer: A
Triangle-Quad Mesh Codec. In Proceedings of
Eurographics 02 Conference, 383-392.
Mukhopadhyay. A., Jing. Q., 2003. Encoding
Quadrilateral Meshes. In Proceedings of 15th
Canadian Conference on Computational Geometry,
Halifax, Nova Scotia, Canada, 60 – 63.
Rossignac, J., 1999. EdgeBreaker: Connectivity
Compression for Triangle Meshes. IEEE Transactions
on Visualization and Computer Graphics, Vol. 5, No.
1, 47–61.
Rossignac, J., Szymczak, A., 1999. Wrap&Zip
decompression of the connectivity of triangle meshes
compressed with EdgeBreaker. Computational
Geometry, Theory and Applications, 119-135.
Touma, C., Gotsman, C., 1998. Triangle Mesh
Compression. In Proceeding of Graphics Interface 98.
GRAPP 2008 - International Conference on Computer Graphics Theory and Applications
38
