DTW-CURVE FOR CLASSIFICATION OF LOGICALLY

SIMILAR MOTIONS

Yang Yuedong, Zhao Qinping

State Key Laboratory of Virtual Reality Technology, Beihang University, Xueyuan Road, Beijing, China

Hao Aimin,Wu Weihe

State Key Laboratory of Virtual Reality Technology, Beihang University, Xueyuan Road, Beijing, China

Keywords: Motion capture, logical classification, hierarchical clustering, DTW, DTW-Curve.

Abstract: Logical classification of motion data is the precondition of motion editing and behaviour recognition. The

typical distance metrics of sequences can not identify logical relation between motions well. Based on the

traditional DTW distance metrics, this paper proposes strategies bidirectional DTW and segment DTW,

both of which could improve the robustness of identifying logically related motions, and then proposes a

DTW-Curve method which is used to compare the logical similarity between the motions. The generation of

DTW-Curve includes three steps. Firstly, motions should be normalized to remove the global translation

and align the global orientation. Secondly, motions are resampled to cluster local frames and remove

redundant frames. Finally, DTW-Curve is generated under the control of different thresholds. DTW-Curve

may produce many statistical properties, which could be used to unsupervised logical classification of

motions. We propose two types of statistical properties, and classify motion data by using hierarchical

clustering procedure. The experiment results demonstrate that the logical classification based on DTW-

Curve has better classification performance and robustness.

1 INTRODUCTION

Motion capture is a popular way of obtaining

realistic motions for games and films. Motion data

are often stored in a motion library with behaviour

labels. Now, the clips need to be labelled and

classified manually. And this way consumes too

much time and energy.

The crucial point in classification is the

definition and judgment of the similarity between

motions. At present, there are two types of

similarity: numerical similarity and logical similarity

(Kovar and Gleicher, 2004, Muller et al., 2005).

Numerical similarity based on numerical comparison

is usually used in motion editing, motion graph and

motion synthesis. But logically similar motions need

not be numerically similar. For example, the motions

of kicking forward and kicking side have different

moving track and are not similar according to

numerical similarity, but they are similar and belong

to the same motion cluster semantically.

The classification based on numerical similarity

is simple, and mature. Dynamic time warping

(DTW) is a typical metric of evaluating the

numerical similarity. The basic idea of DTW is to

find an optimal alignment of two sequences by

stretching them with respect to time. Because DTW

warps the local data, DTW distance (the average of

optimized path) can identify the logical similarity

between two sequences to some extent. Meanwhile

there are two disadvantages of using DTW to judge

the logical similarity between two motions:

(1) Overly Restricted Constraints

DTW restricts searching range of optimized path

to accelerate DTW and avoid illegal problems, such

as non-monotony, discontinuousness and

degeneration (Kovar and Gleicher, 2004). However,

the conditions are overly restrictive for comparing

logical similarity.

(2) Poor Robustness

The DTW distance between two motions is a

numerical value. It is not robust to judge logical

281

Yuedong Y., Qinping Z., Aimin H. and Weihe W. (2008).

DTW-CURVE FOR CLASSIFICATION OF LOGICALLY SIMILAR MOTIONS.

In Proceedings of the Third International Conference on Computer Graphics Theory and Applications, pages 281-289

DOI: 10.5220/0001093702810289

 SciTePress

similarity only by a numerical value because of its

sensitivity to the noise.

Logical similarity was proposed by Kovar (2004)

and was used for motion searching. Muller(2005)

adopted this idea and proposed a better motion

searching method. Muller(2006) further proposed

Motion Template which brought the concept of

logical similarity into motion classification, but MTs

need more training and learning.

The purpose of this paper is to build a simple

logical similarity metric without training. Based on

DTW, we propose two new strategies (bidirectional

DTW and segment DTW) to loosen the constraints,

and propose a DTW-Curve method which can be

used to compare the logical similarity of two

motions without training. DTW-Curve may produce

many statistical properties, which can be used for

unsupervised logical classification of motions. We

propose two kinds of statistical information, and

classified motion data by using hierarchical

clustering procedure. In order to evaluate the

classified results, this paper provides Reward-Punish

Value to evaluate and analyze the results.

2 RELATED WORK

Many scientists have researched in motion data

segmentation and clustering. Lee(2006) used PCA

method to represent low dimensional motion data,

and adopted self-organizing map (SOM) to cluster

these data, finally found Motion Primitives

Segmentation in motion data. Barbic(2004)

presented three models of automatic segmentation:

PCA, PPCA and Gaussian mixture model.

Souvenir(2005) chose Manifold Clustering method

to segment simple behavior motion. Seward (2005)

used non-linear dimension reduction in tangent

space to segment motion data. Jenkins (2002, 2003,

2004) derived the action and behavior primitives

from motion data by using ST-Isomap. The same

action could be clustered and generalized, and

further dimension reduction iterations were applied

to derive extended-duration behaviors.

The common conception in the methods above is

using dimension reduction or clustering to identify

the similarity of motions. The drawbacks of this

conception are that the quantity of data points will

affect the clustering, and that the procedure should

be re-executed if a new motion is concerted.

The logical similarity of motions is mainly used

for motion indexing and identifying. Kovar(2004)

presented a method to locate and extract motion

segments which were logically similar by using

multi-step searching. Muller(2005) proposed a class

of boolean features, called geometric features, to

express the geometric relations between poses. The

geometric features are powerful in describing and

specifying motions at a high semantic level. Based

on the geometric features, Muller(2006) introduced

the concept of motion templates(MTs) to capture the

essence of an entire class of logically related

motions. Although MTs are powerful concept for

classification, they need lots of training and learning

before being used.

Dynamic time warping (DTW) is a technique

frequently used for the optimal alignment of

sequences with given constraints (Cardle

2004)(Ratanamahatana 2005). Bruderlin and

Williams(1995) applied it to animation parameters

in their paper. Subsequent authors used it to align

motion clips before interpolation (Kovar and

Gleicher, 2003). Wang(2004) used time warping to

search appropriate blending length before blending

motion. Keogh (2004) indexed a large human-

motion database by using DTW to align the time

axis. Forbes(2005) found similarities in motion data

using DTW which must pass some seed points.

Hsu(2005) proposed iterative motion warping to

compute dense correspondences between

stylistically different motions. And Hsu(2007)

presented a time-warping technique to simplify the

process of motion editing.

Schödl(2000) searched the transition points in

the video sequences to synthesize new video.

Kova(2002) and Arikan(2002) adopted a similar

method with Schödl to search direct transition points

in motion sequences, and constructed a motion

graph. Gleicher(2003) created a graph structure with

a small number of hub nodes where transitions were

to occur. Inspired by them, we loosen the constraints

of DTW referring to the concept of transition points

and propose the segment DTW to improve the

effectiveness of logical classification.

3 EFFECTIVENESS OF LOGICAL

CLASSIFICATION

Many functions can be used to compare the

similarity of motions. Some of them are effective in

comparing the numerical similarity, and some are

effective in measuring the logical similarity. For the

sake of clarity, we propose two notions to describe

the classification ability of these functions.

(1)Effectiveness of Numerical Classification

(EoNC): EoNC evaluates the performance of a

function on numerical classification. Good

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

282

performance means the function can cluster most of

motions which are numerically similar. DTW has

perfect performance on numerical classification, so

it has a high EoNC. However, logical classification

algorithms may have low EoNC, such as our method,

because they cluster the motions which are not

numerically similar.

(2) Effectiveness of Logical

Classification(EoLC): EoLC is used to evaluate the

performance of a function on logical classification.

If a function has a high EoLC, it can cluster most of

motions which are logically similar.

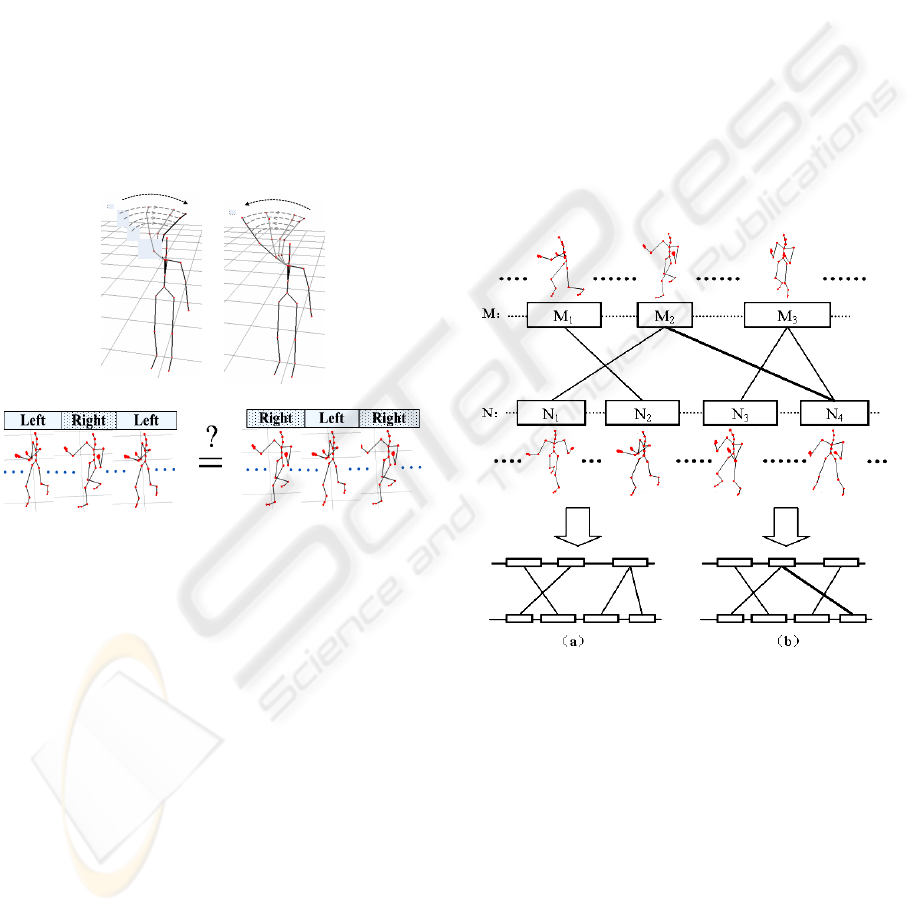
Some motions are similar with their symmetrical

motions. For example, the two motions of

“clockwise waving” and “anticlockwise waving” are

semantically similar to each other, and they belong

to the same motion cluster(Fig.1 a). However, they

may not be similar if evaluated by DTW.

(a)

(b)

Figure 1: Logically similar motions may be numerically

dissimilar. (a): Clockwise waving and anticlockwise

waving. (b): Two cross-similar boxing.

Some motions are cross-similar between their

segments. For instance (Fig.1 b), a boxing motion is

composed of three segments (“left-boxing, right-

boxing” and “left-boxing”). Another boxing motion

is also composed of three segments (“right-boxing”,

“left-boxing” and “right-boxing”). Both of the

boxing motions are regarded as logically similar,

although they have a large DTW distance value.

In this paper, we presente two strategies to

identify the symmetrical similarity and cross-

similarity based on typical DTW.

(1)Bidirectional Dynamic Time Warping (B-DTW)

In general, a motion

123

( , , ,..., )

NGGG G= may

be viewed as logically similar with its symmetrical

motion

12 1

( , , ,..., )

nn n

NGGG G

−−

′

. Mathematically,

given two motions

and N , the DTW distance

between

and N is (,)

dtw

dMN, and the DTW

distance between

and N

′

is (, )

dtw

dMN

′

. Then

the B-DTW distance between

and N is defined

as:

(,)

Bdtw

dMN

−

=min{ (,)

dtw

dMN, (, )

dtw

dMN

′

}

(1)

B-DTW could improve the effectiveness of

logical classification by applying DTW in two

symmetrical directions.

(2)Segment Dynamic Time Warping(S-DTW)

We split the motions into some segments and

compute the B-DTW distance between them. The

S-DTW distance is defined as the minimum sum of

B-DTW distance which could cover all the

segments.

Take two motions

and N (Fig.2) for example.

is segmented into

and

, and N is

also split into four segments:

N ,

N and

N .

Figure 2: Schematic of S-DTW process.

If all the B-DTW distance between the segments

are

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

and

(,)

Bdtw

dMN

−

And

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

There are two ways to sum up the B-DTW distance

and cover all the segments:

(a)

(,)

Sdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(b)

(,)

Sdtw

dMN

−

′

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

DTW-CURVE FOR CLASSIFICATION OF LOGICALLY SIMILAR MOTIONS

283

Because

(,)

Bdtw

dMN

−

(,)

Bdtw

dMN

−

, the S-

DTW distance between

and N is (a).

Because this algorithm need search the minimum

of distance, it will contain lots of iterations. If there

are

jumps (connection in Fig.2) between

and

N , !n times of iteration should be executed and the

worst-case running time is

()

On . In order to

improve the algorithm’s efficiency, we may reduce

the time cost by the condition (“cover all the

segments”) in the definition of S-DTW. If a segment

has only one jump (connection) with other segments,

the total times of iteration will fall to

(1)!n − . This

improvement could reduce the running time by 97%.

4 DTW-CURVE GENERATION

The key of the S-DTW algorithm is splitting the

motions into segments. In this paper, we propose a

novel method of segmentation based on distance

thresholds. Given a threshold, we can identify all the

potential similar segments and obtain S-DTW

distance. As the threshold changes, a set of S-DTW

distance values can be generated, and we define the

set of values as DTW-Curve.

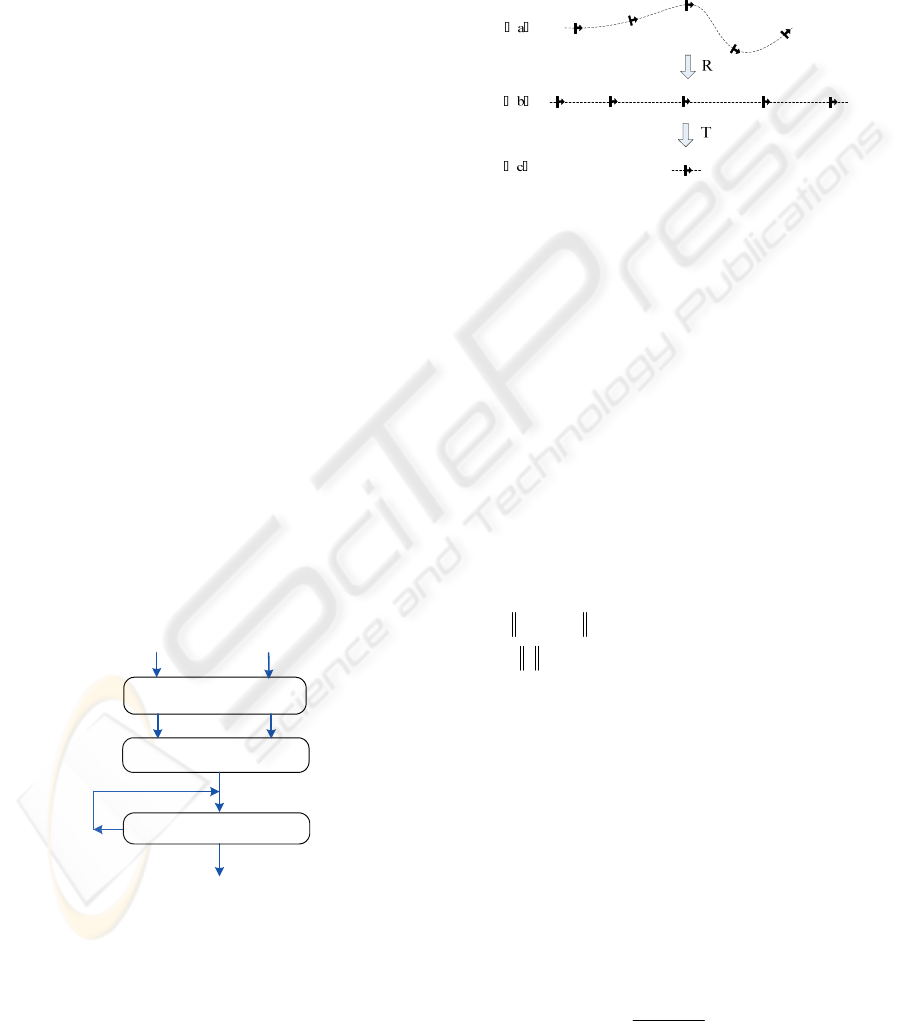
The overview of DTW-Curve generation is

illustrated in Fig.3, which contains three phases.

Given two motions

and N , firstly, they both

should be normalized to remove the global

translation and align the global orientation. Then

they are resampled to cluster local frames and

remove redundant frames. Finally, DTW-Curve is

generated under the control of thresholds.

Motion Data

Normalizing

Resampling

DTW-Curve

Motion Data

S-DTW

threshold

Figure 3: The overview of DTW-Curve generation.

4.1 Normalizing

A motion is fundamentally unchanged by a rotation

about the vertical axis and a translation along the

floor plane. For example, all walking towards

different directions are logically similar. Therefore,

the global translation should be removed and the

orientation should be aligned.

For example, Fig.4(a) is a motion showed in 2D

space. After rotating, each frame of the motion

oriented to the same orientation (Fig.4 b). And after

translating, the roots of all the frames have the same

position (Fig.4 c).

Figure 4: The process of normalizing. (a): A motion

showed in 2D. (b): Align the orientation about the vertical

axis. (c): Remove the global translation.

4.2 Resampling

People are sensitive to high-frequency motion, so

they identify a motion by its high-frequency part.

The low-frequency segments, such as standing,

make less contribution to the classification, and even

result in a wrong classification. For instance, a

motion

is composed of standing and boxing, and

N is composed of standing and kicking. The longer

the standing time lasts, the lower the S-DTW

distance between

and N will be. In order to

overcome this problem, we clustered low-frequency

frames and generated a new motion.

Given a normalized motion

(, ,..., )

FF F= ,

ii i

dFF

∇= −

denotes first order difference,

where

•

is L2 norm. If the sum of

∇

continuous

k frames is less than a user-defined

threshold

, and the sum in continuous

+1 frames

is larger than or equal to

, the k frames will be

clustered into one frame. Mathematically, let

()Cluster M denote the new motion after clustering:

()Cluster M =

,1 ,

( , ,... )

mm mm

GG G

−

(, ,...)

mm m

(2)

where

−

is the

i frame in the new motion

and is generated after clustering the frames (

m to

-1) in the old motion. That is,

−

∑

(3)

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

284

In the clustering process, the parameters

(, ,...)

mm m are specified by the constraints (4)

and (5):

<∇

−−

∑

−

(4)

≥∇

−

∑

−

(5)

The essence of clustering is resampling the

motion and compressing the low-frequency

segments. Although the motion length is shortened,

the high-level behaviour denoted by the motion is

not changed.

For example, a motion (420 frames) is composed

of standing and walking. The distance matrix is

computed between every pair of frames in the

motion (Fig.5 left). After clustering and resampling,

a new motion (78 frames) is generated. The new

distance matrix is illustrated in the right of Fig.5. By

comparing the two figures, we can find the motion

has been compressed without affecting the high-

level behaviour.

Figure 5: Resampling doesn’t change the high-level

behaviour of motion. Left: The distance matrix of initial

motion. Right: The distance matrix of resampled motion.

The clustering not only compresses the motion

and reduces the length, but improves the computing

efficiency. What’s more, the clustering can improve

EoLC, because it only retains the frames which

contribute to the logical classification.

4.3 Creating DTW-Curve

The two motions

( , ,..., )

FF F=

and

( , ,..., )

GG G=

compose a distance matrix

(,)DM N , where the element

(, )

ij F G=−

represents the Euler distance between the

i frame

and

j frame of N .

Given a threshold parameter [0,1]

∈ and the

corresponding threshold

(Fig.6 a).

=(max( (,)DM N )-min( (,)DM N ))

+min(

(,)DM N )

(6)

Several 8-connecting zones(Fig.6 b) are obtained

by eliminating the elements bigger than

in the

distance matrix

. The 8-connecting zone is an

area, in which all points are 8-neighbors and below

the distance threshold in the self-similarity matrix.

The values in every 8-connecting zone are less

than or equal to the threshold

, which means the

two motion segments in the connecting zone are

potentially similar pairs of motion segments. We

define the least enveloped rectangle of the

connecting zone as Least Similar Zone, which is

showed in the shadow rectangle of the fig.6(c).

(a) (b)

Figure 6: The process of creating DTW-Curve. (a): Setting

a threshold parameter. (b): Obtaining several 8-connection

zones. (c): Defining shadow rectangle as Least Similar

Zone. (d): computing the bidirectional DTW distances of

all Least Similar Zones and obtaining the S-DTW distance

under the threshold.

Mathematically, the Least Similar Zone is the

distance matrix of some segments of

and N ,

and its average distance is less than the average

distance of every neighbour distance matrixes with

the same dimension. So the two segments in the

Least Similar Zone are potentially similar.

According to the S-DTW algorithm, we compute the

bidirectional DTW distances of all Least Similar

Zones, and obtain the S-DTW distance

(, , )

Sdtw

dMN

−

between

and N (Fig.6 d),

where

represents threshold parameter,

and N

are the motion sequences which are normalized and

resampled.

[0,1]

∈

is independent of the motion length and

distance range. Generally, the parameter

determines the total area of the Least Similar Zones.

becomes smaller, the total area will become

smaller and the metric error will become larger. But

as the total area becomes larger, the robustness of

method will become poorer.

DTW-CURVE FOR CLASSIFICATION OF LOGICALLY SIMILAR MOTIONS

285

Especially, when the threshold

is equal to 1,

there exists only one Least Similar Zone which is the

distance matrix

(,)DM N . That is,

(1, , )

Sdtw

dMN

−

= (,)

Bdtw

dMN

−

and EoNC is the

largest now.

When

is equal to 0, (0, , )

Sdtw

dMN

−

=0. It

means the value is meaningless to the logical

classification and both of EoNC and EoLC are the

smallest.

increases from 0, EoNC and EoLC

increase gradually. While

is approaching to 1,

EoNC continues to increase, but EoLC decreases

because of the numbers of Least Similar Zones

become reduce. (See Figure 7).

Parameter

Effectiveness

EoNC

EoLC

Figure 7: The EoNC curve and EoLC curve.

Each threshold parameter

is corresponding to

a S-DTW distance, so we will obtain a set of

(, , )

Sdtw

dMN

−

as the threshold

changes. The

distance curve formed by the set of

(, , )

Sdtw

dMN

−

is called DTW-Curve.

When the value of

is close to 0, the EoLC is

too low to be used for classification. So we only

select a segment of DTW-Curve, in which the

threshold

is [0.3, 1].

Because DTW-Curve is formed by a set of S-

STW values, it has a higher EoLC and higher

robustness than a single S-DTW value does.

Therefore, DTW-Curve is a more feasible method to

evaluate the similarity of two motions.

We take an example to further describe the

features of DTW-Curve. Given three motions

jumping1, jumping2 and basketball, we can obtain

DTW-Curves in the threshold parameter range [0.3,

1] (Figure 8).

Figure 8: Comparing the similarity of three motions based

on DTW-Curve. S1 denotes the DTW-Curve between

jumping1 and basketball. S2 denotes the DTW-Curve

between jumping1 and jumping2.

Let

()S

denote DTW-Curve between jumping1

and

basketball, and let

()S

denote DTW-Curve

between

jumping1 and jumping2.

When

=1,

(1)S is almost equal to

(1)S . That

is, judging by the DTW distance, three motions are

logically similar. However, judging by the DTW-

Curve, the logical distance between

jumping1 and

basketball is larger than the logical distance between

jumping1 and jumping2, because the curve

S is

above

S . The result proves that DTW-Curve is

more reasonable than typical DTW for identifying

the logical relationship of motions.

5 LOGICAL CLASSIFICATION

DTW-Curve could produce many statistical

properties, which could be used to unsupervised

logical classification of motion data. In this paper,

we propose two kinds of statistical information, and

classify motion data by using hierarchical clustering

procedure.

(1) Weighted DTW Distance

We take EoLC as the weight, and sum the

distance of DTW-Curve. Mathematically, the

weighted DTW distance is defined as:

(,)

Wdtw

dMN

−

() (, , )

EoLC S dtw

WdMNd

λλ

−

⋅

∫

(7)

We assume the function of EoLC is:

(0.7)/2

00.3

()

0.3 1

EoLC x

σπ

−−

≤

⎧

⎪

⎨

⎪

⎩

(8)

where the standard deviation

is 0.3.

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

286

In order to improve the efficiency, we adopt the

sum of discrete value instead of integral in the

algorithm. We split the parameter

into 8 intervals:

(0,0.3], (0.3,0.4] , (0.4,0.5], (0.5,0.6], (0.6,0.7],

(0.7,0.8], (0.8,0.9] and (0.9,1]. And only a parameter

is selected in each interval randomly.

The distance between the cluster

D and

D is

defined as:

(, )max( (,))

ij Wdtw

dD D d MN

−

∈

(9)

When the minimum of (, )

dD D is larger than

classification threshold

, the procedure will finish.

And the algorithm is also called complete-linkage

algorithm.

(2) Fuzzy Distance

In this algorithm, the distance of motions is

expressed by an interval, called fuzzy distance. The

fuzzy distance is defined as:

[]

(,)dMN

⋅

[,]ab =

[min( ( , , )), max( ( , , ))]

Sdtw Sdtw

dMNdMN

−−

(10)

where

[0.3,1]

∈

Then the distance between the clusters

D and

D is defined as:

(, )[,]

dD D cd==

[] []

[min( (,).),max( (,).)]

dMNa dMNb

⋅⋅

∈

(11)

In the algorithm, there are two parameters:

classification threshold

and fuzzy parameter

. If

the value of

()dc c

−×+ is less than

, the two

clusters can be merged. When fuzzy parameter

0, the algorithm can be called single-linkage

algorithm. And when

is 1, the algorithm can be

called complete-linkage algorithm. In the

implementation, we set

=0.5.

6 EXPERIMENTS AND RESULTS

We implemented our algorithms in Matlab and ran

the experiments on a machine with 1GB of memory

and 2.8 GHz Pentium D processor.

We random selected 80 motion sequences from 6

clusters, and each motion sequence consisted of

about 800 frames. These sequences included 11

basketball, 6 soccer, 7 boxing, 17 jumping, 20

running and 19 walking.

We calculate the DTW distance matrix, weighted

DTW distance matrix and fuzzy distance matrix of

the 80 motion sequences. And we cluster them using

the algorithm in the section 5. As the classification

threshold

changes, we obtain a

- curve (Fig.

9), where

k is the number of clusters.

Figure 9: The

- curves based on three types of

distance.

The Fig.9 illustrates that the logical classification

based on DTW-Curve has some advantages below:

(1) Good performance of classification: When

using traditional DTW distance, the difference

between the threshold value corresponding to the

number of clusters 5 and the threshold value

corresponding to the number 7 is unobvious. That is,

the threshold strip of the number 6 is narrow and has

poor performance of classification. When using the

algorithm proposed in this paper, the threshold strip

of the number 6 is broader and has better

performance.

(2) Good extensibility: We can obtain many

statistical properties from DTW-Curve, and all of

them can be used for classification. That is, the

algorithm proposed in this paper has better

extensibility than traditional DTW.

In order to evaluate the classification error, we

propose an evaluating metric: Reward-Punish Value.

Its main idea is rewarding the classification

algorithm which clusters two motions correctly,

otherwise punishing it. Mathematically, given a

classification algorithm

. It classifies motion

sequences to

clusters, which are

C ,

C ,…, and

C . We define the Reward-Punish Value of

under the numbers of clusters

as:

(, ) ( , )

Pij

kMC

VfK FMM

=∈

∈

≤

∑∑

(12)

Where

DTW-CURVE FOR CLASSIFICATION OF LOGICALLY SIMILAR MOTIONS

287

1()()

(,)

1() ()

cluster M cluster N

FMN

cluster M cluster N

⎧

⎨

−≠

⎩

(13)

If the two motions belong to the same cluster,

=1or else

= -1. When the number of clusters

is 6, we calculate the Reward-Punish Values of three

types of classification algorithm (see Fig. 10) .

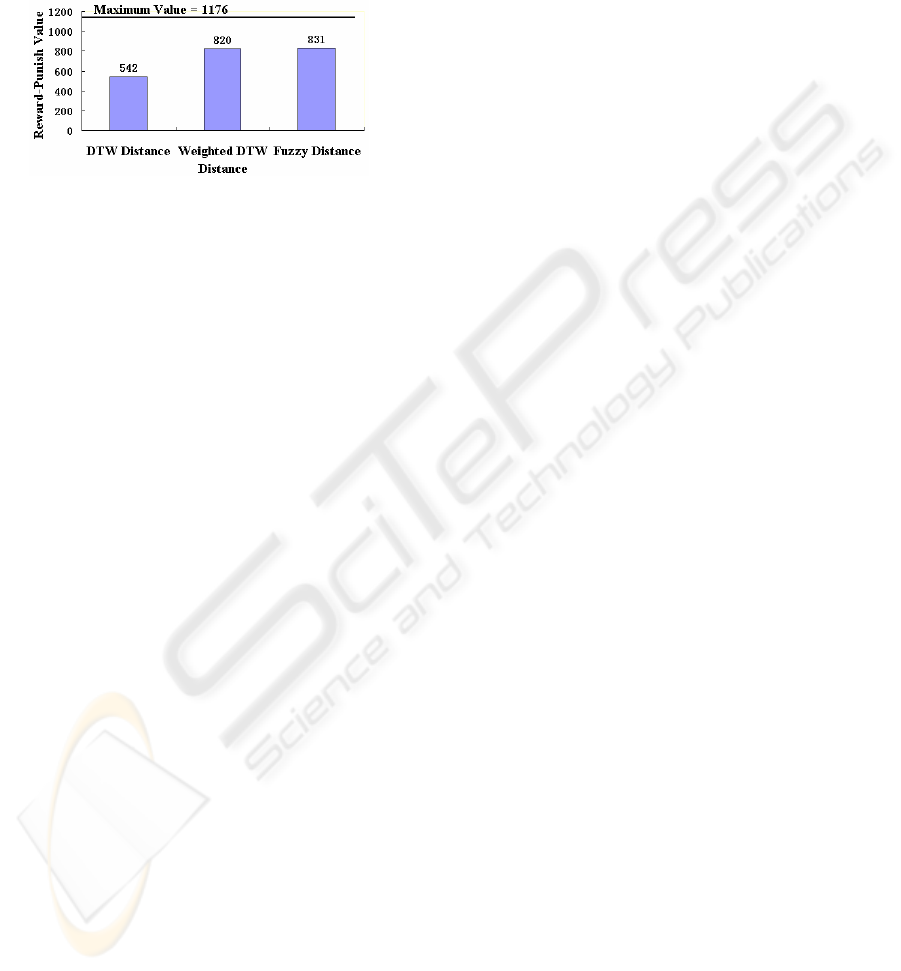
Figure 10: The Reward-Punish Values of three types of

classification algorithm.

The Reward-Punish Value of the best

classification algorithm is 1176. The fig.10

illustrates that all of the three algorithms could not

reach the maximum value, but compared to the

traditional DTW method, the algorithms in this

paper could obtain larger Reward-Punish Values and

the results are closer to the best classification.

7 CONCLUSIONS

Based on traditional DTW distance, this paper

proposed two strategies (bidirectional DTW and

segment DTW) and a method (DTW-Curve) to

compare the motions logical similarity. Comparing

to conventional DTW, DTW-Curve had better

logical classification performance and robustness.

Then we proposed two types of statistical

properties (Weighted DTW Distance and Fuzzy

Distance), and classified motion data by using

hierarchical clustering procedure. And we compared

them with DTW distance metric by using Reward-

Punish Value. The experiment showed that DTW-

Curve method could lead to more reasonable logical

classification results.

Based on the current work, the further work is

probably as follows:

(1) Motion recognition and retrieval. DTW-Curve

can identify logical similarity more effectively, so

we can extend the method to unsupervised motion

recognition and retrieval.

(2) Algorithm efficiency. One major drawback of

DTW-Curve is that it can not be generated real-time

because of lots of iterations. So we should improve

the algorithm efficiency in the future.

ACKNOWLEDGEMENTS

We would like to thank the Graphics Lab. of

Charnegic Mellon University for generously

providing their motion capture data on their web.

This work was supported by China High-tech

Olympics Project (Z0005191041211) and China 863

Project (No. 2006AA01Z333).

REFERENCES

Kovar, L. & Gleicher, M., 2004. Automated extraction and

parameterization of motions in large data sets. In

International Conference on Computer Graphics and

Interactive Techniques. Los Angeles, California, ACM

Press.

Muller, M., Roder, T. & Clausen, M., 2005. Efficient

content-based retrieval of motion capture data. ACM

Trans. Graph., 24, 677--685.

Muller, M. & Roder, T., 2006. Motion Templates for

Automatic Classification and Retrieval of Motion

Capture Data. In Proceedings of the 2006 ACM

SIGGRAPH / Eurographics Symposium on Computer

Animation (SCA 2006). Vienna, Austria, Eurographics

Association.

Lee, C. & Elgammal, A., 2006. Human Motion Synthesis

by Motion Manifold Learning and Motion Primitive

Segmentation. In IV Conference of Articulated Motion

and Deformable Objects (AMDO). Mallorca, Spain,

LNCS.

Barbic, J., Safonova, A., Pan, P., Faloutsos, P., Hodgins, P.

K. & Pollard, N. S., 2004. Segmenting motion capture

data into distinct behaviors. In Proceedings of the

2004 conference on Graphics interface GI '04.

University of Waterloo, Canadian Human-Computer

Communications Society.

Souvenir, R. & Pless, R., 2005. Manifold Clustering. In

Proceedings of the Tenth IEEE International

Conference on Computer Vision (ICCV'05). Beijing,

IEEE Computer Society.

Seward, A. E. & Bodenheimer, P., 2005. Using nonlinear

dimensionality reduction in 3D figure animation. In

Proceedings of the 43rd annual Southeast regional

conference. Kennesaw, Georgia, ACM Press.

Cardle, M., 2004. Technical Report: Automated Motion

Editing. Computer Laboratory, University of

Cambridge, UK.

Ratanamahatana, C. A. and Keogh. E, 2005. Three Myths

about Dynamic Time Warping. In proceedings of

SIAM International Conference on Data Mining (SDM

'05), Newport Beach, CA.

Bruderlin, A. & Williams, L., 1995. Motion signal

processing. In Proceedings of the 22nd annual

conference on Computer graphics and interactive

techniques. ACM Press.

Kovar, L. & Gleicher, M., 2003. Flexible automatic

motion blending with registration curves. In

GRAPP 2008 - International Conference on Computer Graphics Theory and Applications

288

Proceedings of the 2003 ACM

SIGGRAPH/Eurographics symposium on Computer

animation. San Diego, California, Eurographics

Association.

Wang, J. & Bodenheimer, B., 2004. Computing the

duration of motion transitions: an empirical approach.

In Proceedings of the 2004 ACM

SIGGRAPH/Eurographics symposium on Computer

animation. Grenoble, France, Eurographics

Association.

Keogh, E., Palpanas, T., Zordan, V. B., Gunopulos, D. &

Cardle, M., 2004. Indexing Large Human-motion

Databases. In Proceding of the 30th VLDB Conference.

Toronto, Canada.

Forbes, K. & Fiume, E., 2005. An efficient search

algorithm for motion data using weighted PCA. In

Proceedings of the 2005 ACM

SIGGRAPH/Eurographics symposium on Computer

animation. Los Angeles, California, ACM Press.

Hsu, E., Pulli, P. & Popovic, J., 2005. Style translation for

human motion. In International Conference on

Computer Graphics and Interactive Techniques. Los

Angeles, California, ACM Press.

Hsu, E., Silva, M. D. & Popovic, J., 2007. Guided time

warping for motion editing. In Proceedings of the

2007 ACM SIGGRAPH/Eurographics symposium on

Computer animation. San Diego, California,

Eurographics Association.

Schödl, A., Szeliski, R., Salesin, D. H. & Essa, I., 2000.

Video textures. In Proceedings of the 27th annual

conference on Computer graphics and interactive

techniques. , ACM Press.

Kovar, L., Gleicher, M. & Pighin, F., 2002. Motion graphs.

ACM Trans. Graph., 21, 473-482.

Arikan, O. & Forsyth, D. A., 2002. Interactive motion

generation from examples. In Proceedings of the 29th

annual conference on Computer graphics and

interactive techniques. San Antonio, Texas, ACM

Press.

Gleicher, M., Shin, H. J., Kovar, L. & Jepsen, A., 2003.

Snap-together motion: assembling run-time

animations. ACM SIGGRAPH 2003. San Diego,

California, ACM Press.

Jenkins O. C., Mataric M. J., 2002. Deriving Action and

Behavior Primitives from Human Motion Data. In the

IEEE/RSJ International Conference on Intelligent

Robots and Systems. Lausanne, Switzerland,.

Jenkins, O. C. & Mataric, M. J., 2003. Automated

derivation of behavior vocabularies for autonomous

humanoid motion. In Proceedings of the second

international joint conference on Autonomous agents

and multiagent systems. Melbourne, Australia, ACM

Press.

Jenkins, O. C. & Mataric, M. J., 2004. A spatio-temporal

extension to Isomap nonlinear dimension reduction. In

Proceedings of the twenty-first international

conference on Machine learning. Alberta, Canada,

ACM Press.

DTW-CURVE FOR CLASSIFICATION OF LOGICALLY SIMILAR MOTIONS

289