
MUL
TI-DISCRIMINANT CLASSIFICATION ALGORITHM FOR
FACE VERIFICATION
Cheng-Ho Huang and Jhing-Fa Wang
Dept. of Electrical Engineering, National Cheng Kung University, No. 1 University Rd., Tainan City, Taiwan
Keywords:
Linear discriminant analysis, face verification, multi-discriminant classification.
Abstract:
Linear discriminant analysis (LDA) is a conventional approach for face verification. For computing large
amounts of data collected for a given face verification system, this study proposes a multi-discriminant classi-
fication algorithm to classify and verify voluminous facial images. In the training phase, the algorithm extracts
all discriminant features of the training data, and classifies them as the clients’ multi-discriminant sets. The
algorithm verifies a claim to the client’s multi-discriminant set, and then determines whether the claimant is
the client. Comparative results demonstrate that the proposed algorithm reduces the false acceptance rate in
face verification.
1 INTRODUCTION
Two primary applications of face recognition are face
identification and face verification. Face identifica-
tion identifies two similar faces between unknown
user and genuine users; face verification compares an
unknown user to a genuine user, and decides whether
the two are the same. Therefore, impostors present
a problem in face verification. In particular, impos-
tors are greater in number than clients. Eigenface
(Turk and Pentland, 1991) and Fisherface (Belhumeur
et al., 1997) are two of the best known methods that
adopt feature transformation in order to discriminate
differences in facial features for the purpose of face
verification. However, the performance of Eigenface
method is not ideal when numbers of the sample sets
are voluminous. Fisherface, an implementation of lin-
ear discriminant analysis (LDA) (Martinez and Kak,
2001), is often utilized for face verification. It em-
ploys both the PCA and Fisher criterion to extract
discriminant information from a set of training data.
Many methods (Liu and Wechsler, 1998; Loog et al.,
2001; Wang and Tang, 2004) have been proposed to
enhance the performance and stability of LDA. Both
classical and modified LDA methods are efficient for
face recognition.
Although improved LDA approaches are superior
to classical LDA approaches, they still do not provide
adequate discriminant information to permit accurate
discrimination of the highly complex and voluminous
data of facial images. Main reason for this limitation
is given below.
The voluminous data of facial images are not
true Gaussian distributions. Consequently, the clas-
sical linear transform of the “between-class” and the
“within-class” cannot effectively extract the differen-
tial features from the classes.
Therefore, classical LDA is not appropriate for di-
rect analysis of complex and numerous data. As the
amount of data increases, computational loading of
LDA also increases, and the time required for calcu-
lation grows longer, making the method less practi-
cal. To reduce the computations of numerous data,
k-nearest neighbor (KNN) and k-means algorithm are
adopted to classify data into small units. However,
KNN is sensitive to feature mapping; if the feature
mapping is not well distribution, KNN does not ob-
tain robust classifications. K-means , which is an
unsupervised classification algorithm, has problems
with initial centroids and specifying the number of
clusters. Otherwise, if the selected threshold value of
the algorithm is unsuitable, then the false acceptance
rate (FAR) and false rejection rate (FRR) increase; in
particular, the algorithm cannot effectively tune the
threshold parameters for FAR and FRR.
Due to these above-mentioned problems, in order
to avoid the resulting decrease in efficiency of the
overall performance caused by the large amounts of
complex data, this study proposes a verification al-
gorithm without setting any threshold value to sepa-
rate complex data into simple units and verify face
images. This algorithm splits all of the training data,
299
Huang C. and Wang J. (2008).
MULTI-DISCRIMINANT CLASSIFICATION ALGORITHM FOR FACE VERIFICATION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 299-304
DOI: 10.5220/0001082202990304
Copyright
c
SciTePress
enabling each individual’s features to be distinguished
and yield subsets of distinguishable features for each
person. Combining the results obtained by separately
discriminating these subsets is synonymous with ver-
ifying whether an unknown user is the genuine user.
Thus, as evidenced from volumes of face verification,
this study has achieved good efficiency to avoid im-
postors, and increased the overall robustness of the
method.
The paper is organized as follows. Section 2
presents the multi-discriminant classification algo-
rithm on volumes of face verification. Experiments
and final conclusions are provided in Sections 3 and
4, respectively.
2 THE PROPOSED
MULTI-DISCRIMINANT
CLASSIFICATION
ALGORITHM FOR FACE
VERIFICATION
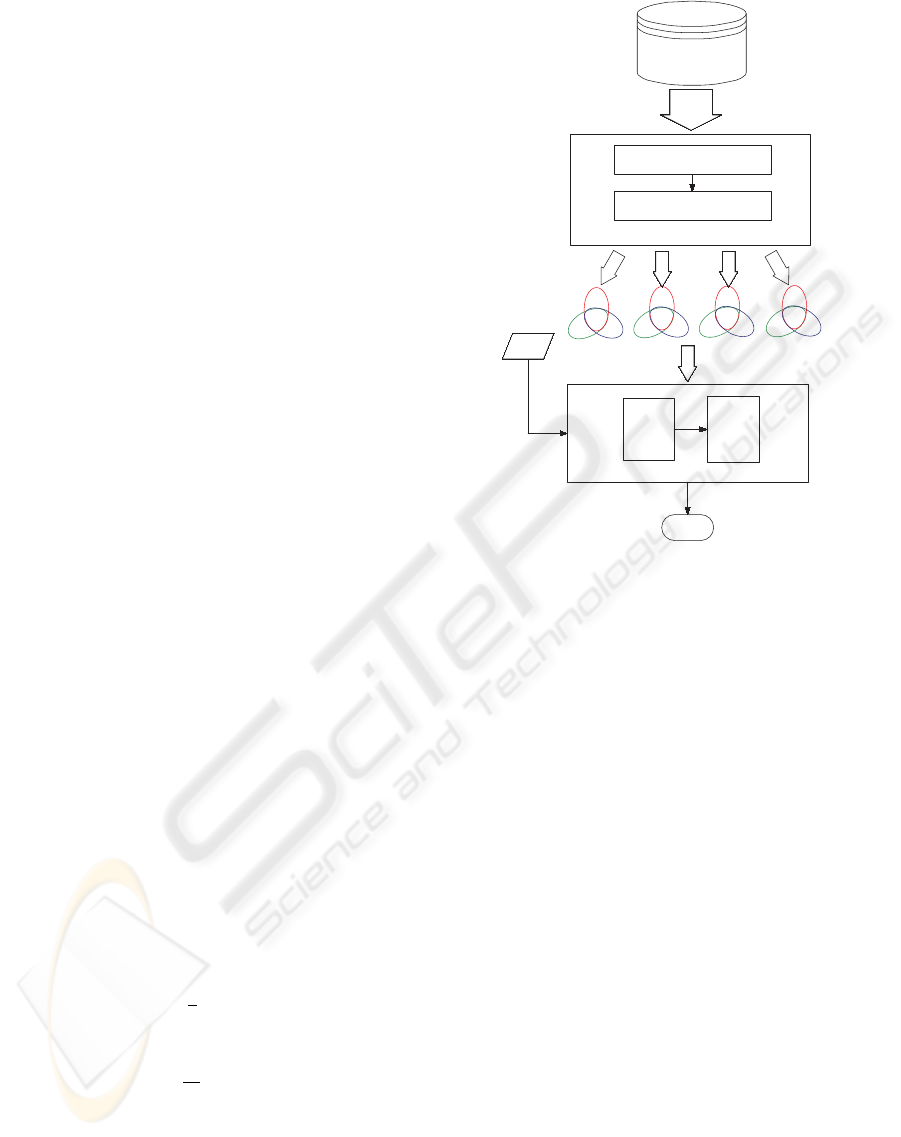
The proposed multi-discriminant classification al-
gorithm (MDCA) consists of two modules, multi-
discriminant classifier and evaluator. Figure 1 shows
the entire framework. Each module is discussed be-
low.
2.1 Multi-discriminant Classifier
The proposed approach using generalized singular
value decomposition LDA (GSVD/LDA) (Howland
and Park, 2004) constructs multi-discriminant sets
(MDS) and performs discriminant analysis to verify
a claimant in the client’s MDS.
Suppose that m-dimensional patterns
A = {x
i
}
i=1,...,n
belong to c different classes
{C
i
}
i=1,...,c
. A ∈ ℜ
m×n
. Let n
k
denote the number of
patterns in class k; thus,
∑
c
k=1
n
k
= n.
µ =
1
n
n
∑
i=1
x
i
, (1)
µ
k
=
1
n
k
∑
x∈C
k
x
k
, (2)
where µ denotes the average of ensemble facial fea-
tures and µ
k
denotes the mean of class C
k
. The
between-class scatter matrix S
B
is defined as
S
B
=
c
∑
k=1
n
k
(µ
k
− µ)(µ
k
− µ)
T
. (3)
x
1
x
2
x
3
x
k
... ...
Result
a claim
... ...
RN
FN
NN
RN
FN
NN
RN
FN
NN
RN
FN
NN
Training Database
Multi-discriminant classifier
Discriminant Feature Extraction
Neighbor Distance Measure
Evaluator
f
x
E
Figure 1: Framework of the proposed algorithm.
The within-class scatter matrix S
W
is defined as
S
W
=
c
∑
k=1
∑
j∈C
k
(x
j
− µ
k
)(x
j
− µ
k
)
T
, (4)
and
S
T
= S
B
+ S
W
. (5)
The transformation matrix G
T
∈ ℜ
l×m
reduces vector
x
i
of A to vector y
i
in the l−dimensional space:
y
i
= G
T
A ∈ ℜ
l×n
,l ¿ m. (6)
The maximum ratio of the between-class to within-
class scatter is obtained by the determinant of the ob-
jective function of the scatter matrices and is defined
as
J(G) = trace((G
T
S
T
G)
†
(G
T
S
B
G)). (7)
When T is full rank,
case 1: l = n
T
†
= (T)
−1
,
case 2: l < n
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
300

T
†
= T
T
(TT
T
)
−1
,
case 3: l > n
T
†
= (T
T
T)
−1
T
T
,
where T = G
T
(S
T
)G and T
†
is the Moore-Penrose
pseudo-inverse can be obtained by GSVD.
The columns of an optimal G comprise the gen-
eralized eigenvectors corresponding to the l largest
eigenvalues in
S
y
B
g
i
= λ
i
(S
y
T
),i = 1,2,...,l (8)
where S
y
B
and S
y
W
are chosen from S
B
and S
W
, respec-
tively; and g
i
is the set of generalized eigenvectors of
S
y
B
and S
y
W
corresponding to the l largest generalized
eigenvalues λ.
The distance measure is derived from the dif-
ferences in features between average face (µ) and
everyone’s (´µ) , and then classifing facial images into
the clients’ MDS. In this case, ´µ = (µ +
1
n
k
∑
n
k
i=1
x
i
)/2.
G
T
is obtained from µ and ´µ in Eq. (7), and the
discriminant feature D is then defined as follows:
if G
T
´µ < G
T
µ
D = −(
°
°
°
G
T
´µ
°
°
°
+
°
°
°
G
T
µ
°
°
°
) (9)
if G
T
´µ > G
T
µ
D
=
°
°
°
G
T
´
µ
°
°
°
+
°
°
°
G
T
µ
°
°
°
(10)
Algorithm 1 illustrates the pseudocode for extract-
ing discriminant features. The clients’ MDS are con-
structed using these differences after extracting the
discriminant features of all faces.
Algorithm 1 The pseudocode of discriminant feature
extraction.
for i=1 to all do
Calculate G
T
i
by Eq. (7).
if G
T
i
´µ < G
T
i
µ then
D
i
← −(
°
°
G
T
i
´µ
i
°
°
+
°
°
G
T
i
µ
°
°
),
else
D
i
←
°
°
G
T
i
´µ
i
°
°
+
°
°
G
T
i
µ
°
°
.
end if
end for
Consider a certain personal set P
S
client
with x mem-
bers. There exist three special subsets NN= {x
i
|i =
P
client
...P
ns
}, FN= {x
j
| j = P
client
...P
f s
} and RN=
{x
m
|m = P
client
...P
rs
}, S = {NN, FN,RN}; where
NN denotes a nearest neighbor subset; FN denotes
a farthest neighbor subset and RN denotes a ran-
dom neighbor subset; ns and f s selections of peo-
ple are similar and non-similar to p
client
, respectively,
and rs denoted the random selections of people to
P
client
. Algorithm 2 illustrates the pseudocode of
multi-discriminant classifier. A subset of t members
is chosen as a subset, where 10 ≤ t ≤ 20.
Algorithm 2 The pseudocode of multi-discriminant
classifier.
for i = 1 to all do
if D
i
∼ D
P
client
and ns ≤ t then
Select x
i
into an NN
P
S
client
.
ns = ns + 1.
end if
if D
i
D
P
client
and f s ≤ t then
Select x
i
into an FN
P
S
client
.
f s = f s + 1.
end if
end for
for rs = 1 to t do
Randomly select x into a RN
P
S
client
.
end for
2.2 The Evaluator of Face Verification
The evaluator determines whether a claim is the client
by an evaluation function on the results of discrimina-
tions from NN, FN and RN.
Equation (11) is a similar description described by
the following expression:
f
x
=
1,
i f dist(x
claim
,x
P
client
)
= min(dist(x
claim
,x))
0,
i f dist(x
claim
,x
P
client
)
> min(dist(x
claim
,x))
(11)
where dist is the distance measure function. If x
claim
is similar to x
P
client
, then f
x
= 1 or 0.
Equation (12) is an evaluation function of MDCA,
and is defined as follows:
E(x
claim
,x
P
client
) = ( f
NN
• f
FN
+ f
RN
)
+ ( f
NN
• f
RN
+ f
FN
)
+ ( f
FN
• f
RN
+ f
NN
),
(12)
where E denotes an evaluator; and • and + are AND
and OR Boolean operators, respectively. If x
claim
is
similar to x
P
client
for two out of the three discriminated
MULTI-DISCRIMINANT CLASSIFICATION ALGORITHM FOR FACE VERIFICATION
301
results of subsets NN, FN, and RN, then x
claim
indi-
cates the genuine user x
P
client
. If E is equal to 1, the
result is an acceptance, or a rejection.
Thus, the face verification problem can be de-
picted by a multi-identification problem. The eval-
uation algorithm is illustrated in Alg. 3.
Algorithm 3 The pseudocode of the evaluator.
Calculate dist(x
claim
,x).
if dist(x
claim
,x
P
client
) = min(dist(x
claim
,x)) then
f
x
P
client
← 1,
else
f
x
← 0.
end if
if E(x
claiim
,x
P
client
) = 1 then
Accept,
else
Reject.
end if
For instance, the statuses of MDS which owns ten
members are described in the Table 1, Table 2 and Ta-
ble 3,respectively. Eq. (12) is used to evaluate x
claim
and x
P
client
, and then obtains E = 1. Therefore, the
result of verification is an acceptance.
Table 1: Select top ten nearest neighbors of D into an NN.
Member D dist() f
P2 282 251 0
P4 247 342 0
P6 217 221 0
P7 371 175 0
P10 391 232 0
P11 182 172 0
P12 389 119 0
P15 193 120 0
P20 387 149 0
P
client
120 76 1
3 EXPERIMENTS
The experiments were carried out on the FERET
(Rizvi et al., 1998), XM2VTS (Messer et al., 1999)
and UNDBD-B (Bowyer and Flynn, 2003) face
databases. FERET is a well-known face database pro-
vided by the NIST. The FERET database contains
994 people and over 11,000 face images, including
profiles, frontal faces, expressions, and poses. The
XM2VTSDB contains 2560 frontal images, which are
four recordings of 295 people taken over a period
Table 2: Select top ten farthest neighbors of D into an FN.
Member D dist() f
P1 891 240 0
P9 777 310 0
P13 909 130 0
P14 1111 171 0
P17 877 234 0
P18 976 140 0
P21 701 127 0
P24 761 134 0
P25 865 182 0
P
client
120 91 1
Table 3: Select ten random neighbors of D into a RN.
Member D dist() f
P3 617 123 0
P5 489 141 0
P8 412 231 0
P13 909 211 0
P15 193 435 0
P16 435 156 0
P19 430 176 0
P22 600 183 0
P23 533 145 0
P
client
120 83 1
of four months. The UNDBD-B database contains
33,247 visible frontal images of 749 people. This
study adopted only the frontal face images as training
faces, and adopted the other types and frontal images
together as test data.
Therefore, the XM2VTS and UNDBD-B were
adopted as the training and testing databases in Ex-
periments (1) and (2), respectively. In Experiment
(3), the FERET database was considered as outside
data to test proposed algorithm. Two evaluations were
adopted to evaluate the system performance:
- False acceptance rate (FAR): the ratio of the
number of false acceptances to that of impostor ac-
cesses.
- False rejection rate (FRR): the ratio of the num-
ber of false rejections to that of authentic accesses.
The experimental results of the proposed face ver-
ification using the MDCA are presented below. In
this evaluation, the sizes of the multi-discriminant sets
were 10 and 20. The MDCA was adopted to verify
these cases in the multi-discriminant sets. The re-
sults in Table 4 indicate that as the FAR and FRR
of NN, FN and RN are decreased as the size of an
multi-discriminant set increases from 10 to 20. In Ex-
periment (1), the optimum value of FAR was 0.34%,
while that of FRR was 4.04%, while the results of
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
302

Table 4: Comparison results of FAR and FRR between MDCA and LDA with KNN.
MDCA LDA
Experiment E Evaluation size with
10 20 KNN (K=10)
FAR 6.25% 5.86%
only NN FRR 4.12% 4.03%
FAR 7.56% 6.91% FAR 12.5%
XM2VTS only FN FRR 4.78% 4.60%
FAR 6.70% 6.30%
(1) only RN FRR 4.71% 4.31%
FAR 0.73% 0.34% FRR 8.7%
NN, FN, RN FRR 4.44% 4.04%
FAR 6.36% 5.91%
only NN FRR 4.33% 4.00%
FAR 7.31% 6.89% FAR 14.7%
UNDBD-B only FN FRR 4.96% 4.36%
FAR 7.23% 6.20%
(2) only RN FRR 5.51% 4.24%
FAR 0.69% 0.23% FRR 11.6%
NN, FN, RN FRR 4.91% 4.11%
FAR 6.41% 5.94%
only NN FRR 4.43% 4.08%
XM2VTS FAR 8.32% 7.38% FAR 16.8%
+UNDBD-B only FN FRR 5.11% 4.21%
+FERET
impostors
FRR 6.64% 6.26%
only RN FRR 4.88% 4.18%
(3) FAR 0.72% 0.31% FRR 13.1%
NN, FN, RN FRR 5.08% 4.18%
the NN, FN and RN intersected together. The FAR
and FRR were 0.23% and 4.11%, respectively in Ex-
periment (2), and 0.31% and 4.18%, respectively in
Experiment (3). Regardless of the results of the NN,
FN and RN, their intersection demonstrated the best
performance in each experiment. The proposed per-
formed better overall than LDA with KNN (Lin et al.,
2005).
4 CONCLUSIONS
This study proposes an algorithm to enhance the face
verification performance in numerous databases by
using multi-discriminant classification. Experimen-
tal results indicate that proposed algorithm elevates
the performance of face verification. Moreover, the
proposed method does not require the construction of
any miscellaneous thresholding rule and can actively
solve the verified problem of face verification. The
experimental results reveal that FAR can be decreased
from 8.32% to 0.31% when utilizing evaluation func-
tion E with three discriminant subsets.
REFERENCES
Belhumeur, P. N., Hespanha, J. P., and Kriegman, D. J.
(1997). Eigenfaces vs. fisherfaces: Recognition using
class specific linear projection. IEEE Trans. on Pat-
tern Analysis and Machine Intelligence, 19(7):711–
720.
Bowyer, K. and Flynn, P. (2003). Univer-
sity of notre dame biometrics database-b.
http://www.nd.edu/ cvrl/UNDBiometricsDatabase.html.
Howland, P. and Park, H. (2004). Generalizing discriminant
analysis using the generalized singular value decom-
position. IEEE Trans. on Pattern Analysis and Ma-
chine Intelligence, 26(8):995–1006.
Lin, D., Yan, S., and Tang, X. (2005). Feedback-based dy-
namic generalized lda for face recognition. Int. Conf.
on Image Processing, 2:922–925.
Liu, C. and Wechsler, H. (1998). Enhanced fisher linear
discriminant models for face recognition. Proc. of the
14th Int. Conf. on Pattern Recognition, 2:1368.
Loog, M., Duin, R. P. W., and Haeb-Umbach, R. (2001).
Multiclass linear dimension reduction by weighted
pairwise fisher criteria. IEEE Trans. on Pattern Anal-
ysis and Machine Intelligence, 23(7):762–766.
Martinez, A. M. and Kak, A. C. (2001). Pca versus lda.
IEEE Trans. on Pattern Analysis and Machine Intelli-
gence, 23(2):228–233.
MULTI-DISCRIMINANT CLASSIFICATION ALGORITHM FOR FACE VERIFICATION
303

Messer, K., Matas, J., Kittler, J., Luettin, J., and Maitre,
G. (1999). XM2VTSDB: The Extended M2VTS
Database. Proc. 2nd International Conference on
Audio- and Video-based Biometric Person Authenti-
cation.
Rizvi, S. A., Phillips, P. J., and Moon, H. (1998). The feret
verification testing protocol for face recognition algo-
rithms. Proc. of the 3rd. Int. Conf. on Face & Gesture
Recognition, page 48.
Turk, M. A. and Pentland, A. P. (1991). Face recognition
using eigenfaces. Proc. IEEE Conf. Computer Vision
and Pattern Recognition, pages 586–591.
Wang, X. and Tang, X. (2004). A unified framework for
subspace face recognition. IEEE Trans. on Pattern
Analysis and Machine Intelligence, 26(9):1222–1228.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
304
