ON THE IMPROVEMENT OF THE TOPOLOGICAL ACTIVE
VOLUMES MODEL
A Tetrahedral Approach
N. Barreira, M. G. Penedo, M. Ortega and J. Rouco
VARPA Group, Department of Computer Science, Universidade da Coru˜na, Spain
Keywords:
3D Image Segmentation, Deformable models, Active models, Topological Active Volumes.
Abstract:
The Topological Active Volumes model is a 3D active model focused on segmentation and reconstruction
tasks. The segmentation process is based on the adjustment of a 3D mesh composed of polyhedra. This
adjustment is guided by the minimisation of several energy functions related to the mesh. Even though the
original cubic mesh achieves good segmentation results, it has difficulties in some cases due to its shape.
This paper proposes a new topology for the TAV mesh based on tetrahedra that overcomes the cubic mesh
difficulties. Also, the paper explains an improvement in the tetrahedral topology to increase the accuracy of
the results as well as the efficiency of the overall process.
1 INTRODUCTION
Deformable models are well-known tools for image
segmentation and reconstruction. They were intro-
duced in 2D by Kass et al. (Kass et al., 1988) and
generalised to 3D by Terzopoulos et al. (Terzopou-
los et al., 1988). The active nets model was first
proposed by Tsumiyama and Yamamoto (Tsumiyama
and Yamamoto, 1989) as a variant of the deformable
models that integrates features of region–based and
boundary–based segmentation techniques. To this
end, this model has two different kind of nodes: in-
ternal nodes, for modelling the inner topology, and
external nodes, for surface adjustment. The former
is related to the region information whereas the latter
uses boundary information. The Topological Active
Volumes (TAV) model (Barreira and Penedo, 2005)
is a 3D extension of the active nets model. It has
an advantage over other models since it not only fits
the surfaces but also models the whole volume. A
TAV consists of a set of nodes organised in a poly-
hedral mesh. Just like any other deformable model,
the mesh deformation is guided by energy functions
in such a way that the mesh energy has a minimum
when the model is over the objects of the scene. Also,
the TAV model is able to perform topological changes
in its structure in order to adjust to concavities, detect
holes, and find separate objects in the scene.
The TAV model, originally developed as a cubic
mesh, achieves goodsegmentation results in both syn-
thetic and real images (Barreira and Penedo, 2004).
The cubic mesh is simple and able to adapt to a
wide range of surfaces. However, in objects with
pronounced curvatures, the cubic mesh has difficulty
in the adjustment due to the four-sided faces of the
cubes. In these cases, a tetrahedral mesh could
fill the space better and, thus, improve the results.
Since tetrahedral meshes are widely used in modeli-
sation and reconstruction (Archip et al., 2006; Sitek
et al., 2006) as well as in segmentation tasks with de-
formable models (Sermesant et al., 2003; Pons and
Boissonnat, 2007), this paper proposes a new mesh
topology for the TAV model based on tetrahedra. The
development of a mesh topology is not straightfor-
ward and implies new ways of initialising and per-
forming topological changes in the structure. Also,
since the new node relationships affect the calculus
of the energies, they have influence on the computa-
tion times. For this reason, some improvements were
developed in order to increase the efficiency of the
model.
This paper is organised as follows. Section 2 ex-
plains the characteristics of the model and the seg-
mentation process. Section 3 introduces the tetrahe-
dral topology as well as the strategy developed to im-
prove the results. Section 4 shows some results of the
529
Barreira N., G. Penedo M., Ortega M. and Rouco J. (2008).
ON THE IMPROVEMENT OF THE TOPOLOGICAL ACTIVE VOLUMES MODEL - A Tetrahedral Approach.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 529-534
DOI: 10.5220/0001081305290534
Copyright
c
 SciTePress

new topology. Finally, section 5 explains the conclu-
sions and the future work.
2 MODEL
A Topological Active Volume (TAV) is a three-
dimensional structure composed of interrelated nodes
located at the vertices of a polyhedron (Barreira and
Penedo, 2005). This polyhedron is repeated through-
out the mesh and defines the neighbouring relation-
ships among nodes. There are two types of nodes:
internal, inside the mesh, and external, on the sur-
faces. Each type of node represents different object
features. The external nodes fit the surface of the ob-
ject whereas the internal nodes model its inner topol-
ogy. Figure 1 depicts a TAV where the repeated poly-
hedron is a cube.
Parametrically, a TAV is defined as v(r, s, t) =
(x(r, s, t), y(r, s, t), z(r, s, t)), where (r, s, t) ∈ ([0, 1] ×
[0, 1] × [0, 1]). The state of the model is governed by
an energy function defined as follows:
E(v) =
R
1
0
R
1
0
R
1
0
E
int
(v(r, s, t)) + E
ext
(v(r, s, t))drdsdt
(1)
where E
int
and E
ext
are the internal and the external
energy of the TAV, respectively. The former controls
the shape and the structure of the net. Its calculus
depends on first and second order derivatives which
control contraction and bending, respectively. The in-
ternal energy term is defined by:
E
int
(v(r, s, t)) =
α(|v
r
(r, s, t)|
2
+ |v
s
(r, s, t)|
2
+ |v
t
(r, s, t)|
2
) +
β(|v
rr
(r, s, t)|
2
+ |v
ss
(r, s, t)|
2
+ |v
tt
(r, s, t)|
2
) +
2γ(|v
rs
(r, s, t)|
2
+ |v
rt
(r, s, t)|
2
+ |v
st
(r, s, t)|
2
)
(2)
where subscripts represent partial derivatives and α,
β and γ are coefficients that control the smoothness of
the net. In order to compute the energy, the parameter
domain [0, 1] × [0, 1] × [0, 1] is discretized as a regu-
lar grid defined by the internode spacing (k, l, m) and
the first and second derivativesare estimated using the
finite differences technique in 3D.
E
ext
represents the characteristics of the scene that
guide the adjustment process and is defined as fol-
lows:
E
ext
(v(r, s, t)) = ωf[I(v(r, s, t))]
+
ρ
|ℵ(r,s,t)|
∑
p∈ℵ(r,s,t)
1
||v(r,s,t)−v(p)||
f[I(v(p))]
(3)
where ω and ρ are weights, I(v(r, s, t)) is the intensity
value of the original image in the position v(r, s, t),
f is a function related to the image intensity, and
ℵ(r, s, t) is the neighbourhood of the node (r, s, t).
This way, given that the repeated polyhedron in the
mesh defines the node neighbourhoods, the shape of
Figure 1: A 4 × 4 × 3 TAV mesh where the base polyhe-
dron is a cube. The dark nodes represent the external nodes
whereas the light ones are the internal nodes.
the polyhedron influences not only the flexibility of
the mesh, but also the way the nodes are adjusted to
the objects.
Since the internal and external nodes model differ-
ent parts of the objects, f should be adapted for both
types of nodes. On one hand, if the objects to detect
are dark and the background is light, the energy of an
internal node will be minimum when it is on a point
with a low grey level. On the other hand, the energy
of an external node will be minimum when it is on a
discontinuity and on a light point outside the object.
In this situation, function f is defined as:
f[I(v)] =







h[I(v)
n
] for internal nodes
h[I
max
− I(v)
n
+ ξ(G
max
− G(v))]
+GD(v) for external nodes
(4)
where ξ is a weighting term, I
max
and G
max
are the
maximum intensity values of image I and the gradient
image G, respectively, I(v) and G(v) are the intensity
values of the original image and the gradient image in
the node position v(r, s, t), I(v)
n
is the mean intensity
in a n× n × n cube, h is an appropriate scaling func-
tion, and GD(v) is the gradient distance, this is, the
distance from the node position v(r, s, t) to its nearest
edge.
Otherwise, if the objects are bright and the back-
ground is dark, the energy of an internal node will be
minimum when it is on a point with a high grey level
and the energy of an external node will be minimum
when it is on a discontinuity and on a dark point out-
side the object. In such a case, function f is defined
as:
f[I(v)] =







h[I
max
− I(v)
n
] for internal nodes
h[I(v)
n
+ ξ(G
max
− G(v))]
+GD(v) for external nodes
(5)
where the symbols have the same meaning as in equa-
tion 4.
The segmentation process consists of several
stages. First, a mesh with an homogeneous distribu-
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
530

tion of nodes is created and located over the whole im-
age. Then, the mesh energy is minimised iteratively
using a greedy algorithm. The energy functions reach
a minimum when the mesh is located around the ob-
jects. After that, the number of nodes in each axis
is recomputed to adapt the mesh size to the object
size; for example, if the object is longer than wider,
the number of nodes in the x-axis will be increased
whereas the number of nodes in the y-axis will be
decreased. The mesh is also centred over the de-
tected objects and its energy is minimised again. Fi-
nally, topological changes are performed to increase
the flexibility of the model and, after a local energy
minimisation step (Barreira et al., 2006), to adjust the
mesh to concave surfaces, holes, or separate objects.
The topological changes involve the breaking of
links between external nodes wrongly located, this
is, external nodes far away from the objects. These
nodes are identified and sorted by their distance to the
objects in order to break the links between the worst
located nodes (Barreira and Penedo, 2005). However,
some link breakings are not allowed because of the
fact that the mesh should keep the polyhedral struc-
ture since isolated nodes or planes does not provide
volumetric information.
3 TETRAHEDRAL MESHES
The TAV model has been developed using a cube
as the base polyhedron of the mesh. Even though
the segmentation results using this configuration were
good (Barreira and Penedo, 2004), the topology based
on cubes has limitations in the adjustment to surfaces.
Specifically, the four-sided faces of the cubes have
difficulty in the adjustment to pronounced curvatures.
Although this problem can be partly solved by in-
creasing the density of nodes, a new mesh topology
that could improve the segmentation results is nec-
essary. Figure 2 shows the reconstruction of an ob-
ject with several small holes that the cubic topology
is not able to detect with a small mesh size and de-
tects roughly with a larger mesh size.
The triangular meshes have the advantage of be-
ing able to model very complex geometries so that
they can improve the results of a quadrilateral mesh.
Therefore, most of the surface reconstruction tech-
niques use triangular meshes to represent surfaces.
Since the TAV model works in 3D with polyhedra,
the new mesh topology will consist of triangle-based
polyhedra, this is, tetrahedra.
Given that there are five tetrahedra in a cube (see
figure 3), the tetrahedral mesh is built from a cubic
mesh in such a way that each cube is the specular im-
Figure 2: Adjustments of meshes based on cubes and tetra-
hedra. First row: original object. Second row: results using
a cubic mesh. Third row: results with tetrahedral meshes.
The meshes have 10× 10× 10 nodes in the first column and
20 × 20 × 20 in the second one. The tetrahedral mesh is
able to detect the small rounded holes in the surface of the
object even with the 10× 10× 10 mesh. On the contrary,
although the results are improved when the mesh size is in-
creased, the cubic mesh only detects roughly the holes with
the 20× 20× 20 mesh.
age of its neighbours. Figure 4 shows an example of
a tetrahedral mesh with 3× 3× 3 nodes.
The mesh topology change does not affect the seg-
mentation process whereas the accuracy of the results
is improved as figure 2 shows. Nevertheless, the new
neighbourhoodof the nodes will affect the calculus of
the external energy function (see eq. 3) in the minimi-
sation stage. Since the number of neighboursgrowsin
the tetrahedral meshes and the calculus of the external
energy depends on the neighbourhood,the tetrahedral
meshes will be slower than the cubic meshes.
In order to speed up the adjustment process and
given that the cubic meshes often produce good re-
sults, a mixedapproach has been developed in this pa-
per. In this approach, the segmentation process starts
with a cubic mesh. Its energy is minimised and, after
that, its size is recomputed. When the minimisation
ON THE IMPROVEMENT OF THE TOPOLOGICAL ACTIVE VOLUMES MODEL - A Tetrahedral Approach
531

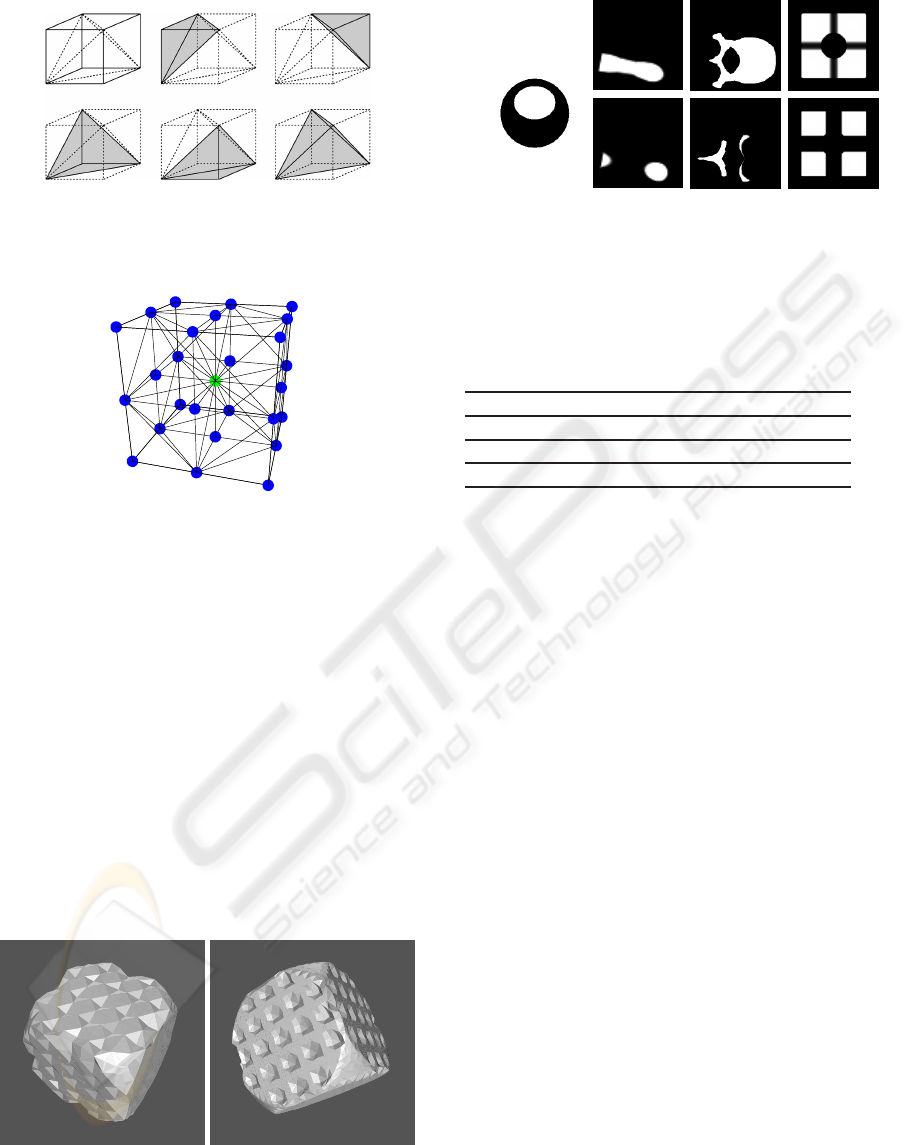
Figure 3: Decomposition of a cube in five tetrahedra. The
tetrahedral mesh is built from this decomposition and its
specular image.
Figure 4: A tetrahedral mesh with 3×3×3 nodes. The dark
nodes are the external nodes whereas the light central one is
the internal one.
process finishes for the second time, the cubic mesh is
able to detect the objects but maybe an improvement
in the adjustment is needed. At this point, a tetrahe-
dral mesh is built from the adjusted cubic mesh and
its energy is minimised again. This way, the cubic
mesh obtains a coarse but fast segmentation whereas
the tetrahedral mesh achieves a fine adjustment. Fig-
ure 5 shows how the mixed approach is also able to
detect the small holes in the object in figure 2 as ac-
curately as the the tetrahedral approach.
Regarding the topological changes, only break-
ings that preserve the tetrahedral structure are al-
lowed. To this end, the mesh integrity is checked
Figure 5: Adjustments of the mixed approach. Left image
was segmented with a 10 × 10 × 10 mixed mesh and the
right one, with a 20 × 20 × 20 mesh. The results of both
tetrahedral and mixed approaches are equivalent.
(a) (b) (c) (d)
Figure 6: Some slices of the 3D images used in the exam-
ples. Slices (a), (b), (c), and (d) correspond to the images in
figures 7, 8, 9, and 10, respectively.
Table 1: Parameters used in the examples.
Figures α β γ ρ ω ξ
7 1.5 10
−5
10
−5
3.0 3.0 5.0
8 3.5 10
−5
10
−5
4.0 3.0 6.0
9 2.0 10
−4
10
−4
4.0 4.0 6.0
10 3.0 10
−5
10
−5
3.0 3.0 5.0
before each breaking. This way, a link between two
nodes is broken only if all their neighboring nodes
belong to, at least, another tetrahedron after the link
breaking.
4 RESULTS
This section shows the results of applying the tetrahe-
dral meshes to several synthetic images. A 3D image
is built as a set of 2D stacked images. Figure 6 shows
some slices of the images used in the segmentation
examples. The input image was used in the calculus
of the external energy for both internal and external
nodes. The gradient images were computed using a
3D Canny detector. The model parameters, empiri-
cally chosen, are summarised in table 1. Since the
mixed strategy is faster than the tetrahedral approach
and produces similar results, all the tetrahedral results
in this section were obtained using the mixed strategy.
The efficiency and the adjustment of the topolo-
gies developed were analysed. With this aim, sev-
eral segmentation processes with different mesh sizes
were performed and the computation times of the cu-
bic, tetrahedral, and mixed approaches were com-
pared. The processes were run in an Intel Core 2
Duo at 2.40 GHz. The graphs in figures 7, 8, and
9 show the computation times of the adjustment pro-
cesses, prior to the stage of topological changes, for
three example images. The graphs show that not only
the computation times of the mixed segmentations
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
532

1000 2000 3000 4000
Nodes
0
500
1000
1500
2000
2500
3000
Computation times (s)
Mixed
Tetrahedron
Cube
Figure 7: Segmentation results in a synthetic image. Top:
results of the cubic (left) and the mixed (right) approaches.
In both cases, the initial meshes had 10 × 10 × 10 nodes.
Bottom: evolution of the computation times of the mesh
topologies with respect to the average mesh size of the ini-
tialisation and readjustment stages. The tetrahedral mesh
produces a more accurate adjustment to the hole surfaces.
1000 1500 2000 2500 3000 3500
Nodes
0
200
400
600
800
1000
1200
Computation times (s)
Mixed
Tetrahedron
Cube
Figure 8: Segmentation of a synthetic object. Top: results
with an initial 9 × 9 × 9 cubic mesh (left) and an initial
12× 12× 12 mixed mesh (right). Bottom: evolution of the
computation times of the mesh topologies with respect to
the average mesh size of the initialisation and readjustment
stages. The adjustment of the tetrahedral mesh is more ac-
curate in the concave area.
3000 4000 5000 6000
Nodes
0
1000
2000
3000
4000
5000
Computation times (s)
Mixed
Tetrahedron
Cube
Figure 9: Segmentation of a vertebra. Top: results of the cu-
bic (left) and mixed (right) approaches. The initial meshes
had 13× 13× 13 nodes. Bottom: evolution of the computa-
tion times of the mesh topologies with respect to the average
mesh size of the initialisation and readjustment stages. The
tetrahedral mesh produces better results since it detects both
lateral prominent areas of the vertebra.
are lower and similar to the cubic ones, but also the
time increase as the mesh size grows is greater in the
case of the tetrahedral meshes. Also, the tetrahedral
meshes improve the adjustment to surfaces.
Figure 10 shows a special case where the object
covers almost the whole image. In these cases, the
mixed strategy produces higher computation times
than the cubic approach. The mixed approach only
uses the fast cubic approach to detect the objects. For
this reason, when the objects cover the whole im-
age, the cubic step is very short and the adjustment
is achieved mainly by means of the tetrahedral mesh.
This way, the computation times for both mixed and
tetrahedral approaches are similar. Nevertheless, the
improvement in the surface adjustment justifies the
use of a tetrahedral mesh.
5 CONCLUSIONS
This paper proposes a new topology for the Topolog-
ical Active Volumes model. The former TAV topol-
ogy based on cubes has limitations to achieve a fine
adjustment to curved surfaces. For this reason, a new
topologybased on tetrahedra was developed. The new
topology behaves like the cubic one, this is, the tetra-
hedral topology is able to detect several objects in the
scene and to adjust to object concavities and holes.
ON THE IMPROVEMENT OF THE TOPOLOGICAL ACTIVE VOLUMES MODEL - A Tetrahedral Approach
533

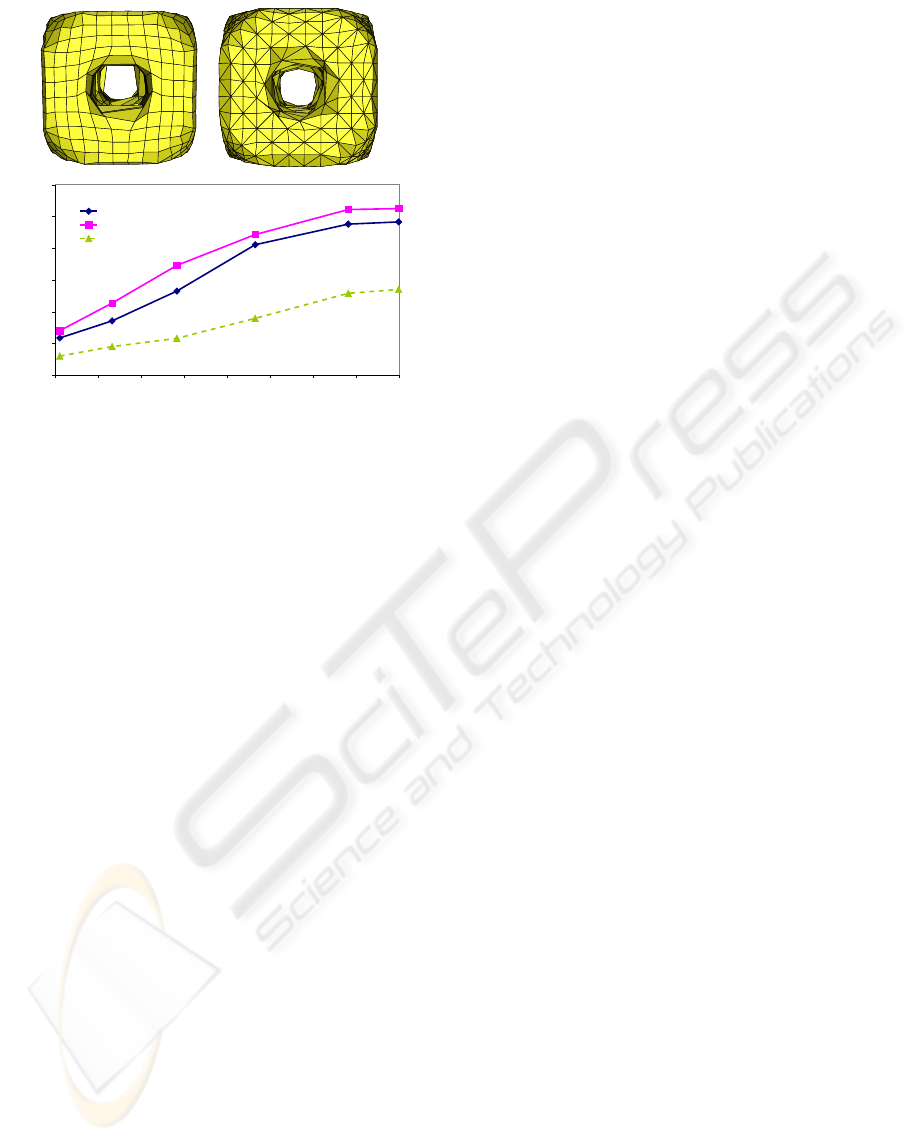
600 800 1000 1200 1400 1600 1800 2000 2200
Nodes
0
100
200
300
400
500
600
Computation times (s)
Mixed
Tetrahedron
Cube
Figure 10: Segmentation of a cube with holes. Top: seg-
mentation results with a cubic mesh (left) and a mixed
(right) mesh of 11× 11× 11 nodes. Bottom: evolution of
the computation times of the mesh topologies with respect
to the average mesh size of the initialisation and readjust-
ment stages. The mixed and tetrahedral approaches have
similar computation times because the object covers the
whole image.
However, the new relationships between nodes in the
tetrahedral meshes imply a higher complexity in the
segmentation process as well as an increase in the
computation time. In order to overcome these draw-
backs, a new strategy was proposed. A mixed topol-
ogy that combines a cubic mesh for a fast and rough
segmentation and a tetrahedral mesh for a fine adjust-
ment. This strategy not only reduces the computation
times, but also improves the results of the segmenta-
tion process.
Future work includes the development of tech-
niques to change the structure of the tetrahedral mesh
by means of inserting or removing nodes in order to
achieve a fine adjustment to complex areas.
ACKNOWLEDGEMENTS
This paper has been partly funded by the
Xunta de Galicia through the grant contracts
PGIDIT05SIN001E and PGIDIT06TIC10502PR.
REFERENCES
Archip, N., Rohling, R., Dessenne, V., Erard, P.-J., and
Nolte, L.-P. (2006). Anatomical structure modeling
from medical images. Computer Methods and Pro-
grams in Biomedicine, 82(3):203–215.
Barreira, N. and Penedo, M. G. (2004). Topological Active
Volumes for Segmentation and Shape Reconstruction
of Medical Images. Image Analysis and Recognition:
Lecture Notes in Computer Science, 3212:43–50.
Barreira, N. and Penedo, M. G. (2005). Topological Ac-
tive Volumes. EURASIP Journal on Applied Signal
Processing, 13(1):1937–1947.
Barreira, N., Penedo, M. G., and Penas, M. (2006). Local
energy minimisations: An optimisation for the topo-
logical active volumes model. In First International
Conference on Computer Vision Theory and Applica-
tions, volume 1, pages 468–473.
Kass, M., Witkin, A., and Terzopoulos, D. (1988). Active
contour models. International Journal of Computer
Vision, 1(2):321–323.
Pons, J.-P. and Boissonnat, J.-D. (2007). Delaunay de-
formable models: Topology-adaptive meshes based
on the restricted delaunay triangulation. In IEEE Con-
ference on Computer Vision and Pattern Recognition,
Minneapolis, USA.
Sermesant, M., Forest, C., Pennec, X., Delingette, H., and
Ayache, N. (2003). Deformable biomechanical mod-
els: Application to 4D cardiac image analysis. Medi-
cal Image Analysis, 7(4):475–488. PMID: 14561552.
Sitek, A., Huesman, R., and Gullberg, G. (2006). Tomo-
graphic reconstruction using an adaptive tetrahedral
mesh defined by a point cloud. IEEE Transactions
on Medical Imaging, 25(9):1172 – 1179.
Terzopoulos, D., Witkin, A., and Kass, M. (1988). Con-
straints on deformable models: Recovering 3D shape
and nonrigid motion. Artificial Intelligence, 36(1):91–
123.
Tsumiyama, K. and Yamamoto, K. (1989). Active net: Ac-
tive net model for region extraction. IPSJ SIG notes,
89(96):1–8.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
534