
A NEW RELIABILITY MEASURE FOR ESSENTIAL MATRICES
SUITABLE IN MULTIPLE VIEW CALIBRATION
Jaume Verg´es-Llah´ı
ATR Intelligent Robotics and Communication Laboratories, Kyoto 619-0288, Japan
jverges@atr.jp
Daniel Moldovan
NICT Universal Media Center and ATR CIS Laboratories, Kyoto 619-0288, Japan
danielm@atr.jp
Toshikazu Wada
Dept. of Computer & Communication Science, Wakayama University, Wakayama 640-8510, Japan
twada@ieee.org
Keywords:
Epipolar geometry, reliability measure, essential matrix, camera-dependency graph.
Abstract:
This paper presents a new technique to recover structure and motion from a large number of images acquired
by an intrinsically calibrated perspective camera. We describe a method for computing reliable camera motion
parameters that combines a camera–dependency graph, which describes the set of camera locations and the
feasibility of pairwise motion calculations, and an algorithm for computing the weights on the edges of this
graph. A new criterion for evaluating the reliability of the essential matrices thus produced with respect to the
epipolar constraint is here introduced. It is composed of two main elements, namely, the uncertainty of the
renormalization process by which the essential matrix is derived and the error between the estimated matrix
and its decomposition into the motion parameters of translation and rotation. Experimental results show that
there exists a clear correlation between the proposed reliability measure and the error in the estimation of such
motion parameters. The performance of the proposed method is demonstrated on a sequence of short base-line
images where it is made clear that the strategy based on the shortest paths in terms of unreliability provides
remarkably superior results to those obtained from the paths of consecutive camera locations.
1 INTRODUCTION
The purpose of calibration from multiple views con-
sists in recovering the spacial location of a certain set
of points along with the determination of the position
of the camera from where these points were viewed.
Despite the problem of obtaining such a 3D struc-
ture from the motion of a camera has been exten-
sively studied for the last two decades (Hartley and
Zisserman, 2003) it is remarkable that any previous
approaches based their strategies on choosing consec-
utive views rather than on a more advantageous com-
bination, that is, the one that would provide the least
recovery error. It seems therefore quite advisable to
try to establish a feasible mechanism for indirectly
estimating this error as a mean of selecting the best
among all such combinations.
This paper is focused on the proposal and justi-
fication of a new measure of reliability that captures
the error of the recovered 3D structure and the camera
movement between a pair of views which is suitable
for carrying out a multiple view calibration. The main
idea is to employ this measure for the purpose of eval-
uating beforehand an estimation of the validity of a
certain pair of views and collecting such information
in the process of selection of the best combination of
views that provides the least recovery error between
two given camera locations.
In general, it is known that the accuracy of the es-
timation of both the motion parameters and the recov-
ered structure may greatly degrade when an increas-
ing number of closely consecutive views are added
into the computations. This is mainly due to inac-
curacies accumulated throughout as well as to short
baselines. Nevertheless, the larger the baseline is, the
better the accuracy should become. Hence, the pairs
of views that must be taken into account in the com-
putations should be as apart each other as possible to
improve the recovery results. In the purpose of effi-
ciently considering all possible combinations of cam-
114
Vergés-Llahí J., Moldovan D. and Wada T. (2008).
A NEW RELIABILITYMEASURE FOR ESSENTIAL MATRICES SUITABLE IN MULTIPLE VIEWCALIBRATION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 114-121
DOI: 10.5220/0001078301140121
Copyright
c
SciTePress

era locations, we suggest the usage of the graph struc-
ture we call Camera–Dependency Graph (CDG).
The CDG is composed of a set of nodes represent-
ing each view of the scene taken from a different lo-
cation of the camera, whereas the weight on the edges
corresponds to the degree of reliability of the pair of
views being connected. Since the measure proposed
in this paper will be shown to closely correlate with
the recovery error, it is suggested that the most trust-
worthy sequence of views, in other words, the one
with the smallest error, would be obtained by select-
ing the path in CDG that minimizes the total amount
of unreliability, since it is that measure which is a in-
direct estimator of the recovery error.
The characterization of the unreliability of a cam-
era pair is carried out by estimating the uncertainty of
its epipolar constraint, i.e., the relative position and
orientation of the camera. This is accomplished by
way of two partial error estimations. The first one en-
compass the error produced in the iterative correction
by which the essential matrix is obtained. The second
comes from the decomposition of this matrix into a
translation vector and a rotation matrix. In this paper
we will show how the combination of these two val-
ues correlates with the recovery error in most of cases.
As a consequence, the proper selection of viewsbased
on such a measure will improve the accuracy of the
recovered structure and motion.
This paper is organized as follows. First, a review
of some previous works in a similar problem is car-
ried out, followed by the description and justification
of the measure of unreliability proposed here. After-
wards, the experimental section will be described as
well as the results obtained for the purpose of con-
firming our claims. This section will focus in two as-
pects, namely, the proof of the correlation between
our criterion and the recovery error, and the usage
of CDG as a route through substantially better multi-
ple view calibrations. Finally, the conclusions drawn
from the obtained results will be discussed along with
the future work necessary to fulfil this research.
2 PREVIOUS WORK
The only attempt to our knowledge of evaluating the
epipolar constraint quality to estimate a multiple view
reconstruction is that of Martinec & Pajdla (Mar-
tinec and Pajdla, 2006). They introduced a so called
reliability–importance matrix in which the reliability
is based on the number of supporting inliers and the
importance, on finding the shortest paths in a graph
induced by a known epipolar geometry. Compara-
tively, our work employs a different approach for the
unreliability which estimates how close the epipolar
constraint is fulfilled by the resulting motion parame-
ters as a combination of the uncertainty of the essen-
tial matrix and its decomposition error.
Chronologically, multiple view reconstruction
was approached for the first time by Tomasi and
Kanade (Tomasi and Kanade, 1992) that used factor-
ization on affine cameras. An extension for perspec-
tive cameras was given later in (Sturm and Triggs,
1996). Perspective effect was handled using both
epipolar geometry (Sturm and Triggs, 1996; Schaf-
falitzky and Zisserman, 2002; Martinec and Pajdla,
2005) and trifocal tensor (Fitzgibbon and Zisserman,
1998). In all these methods, points need to be visible
in at least three views so as to glue partial reconstruc-
tions. Otherwise, a sequence of independently com-
puted fundamental matrices or trilinear tensors might
be optimally consistent with the image data, but not
necessarily consistent with a unique camera trajec-
tory. This is an important constraint on views.
The study of the essential matrix as a method of
determining the epipolar geometry was initially per-
formed in (Longuet-Higgins, 1981) and later general-
ized in (Luong and Faugeras, 1996) by the introduc-
tion of fundamental matrix when internal camera pa-
rameters were unknown. Two different methods for
estimating the stability of fundamental matrix were
introduced in (Csurka et al., 1997), namely, a sta-
tistical one and an analytical one. The first proce-
dure yielded better results in case the noise level of
data was known, despite this is not the usual case be-
sides being computational expensive, while the sec-
ond method performed better if the noise was moder-
ate.
A different approach was introduced by Kanatani
in (Kanatani, 2000). Starting from the same linear
hypothesis describing the epipolar constraint, he de-
rived a nonlinear optimization method whose optimal
unbiased estimate was computed based on an itera-
tive process of renormalization without enforcing the
rank constraint. The obtained solution was afterwards
corrected in order to fulfil that constraint. Experi-
ments indicated that the obtained estimates were in
the vicinity of the theoretical accuracy bound. This
work is the origin of our work, which has been ex-
tended to encompass more complex calibrations de-
scribed by the paths in CDGs.
3 CAMERA-DEPENDENCY
GRAPH (CDG)
In this section we introduce the new concept of
Camera–Dependency Graph (CDG) suitable to com-
A NEW RELIABILITY MEASURE FOR ESSENTIAL MATRICES SUITABLE IN MULTIPLE VIEW CALIBRATION
115
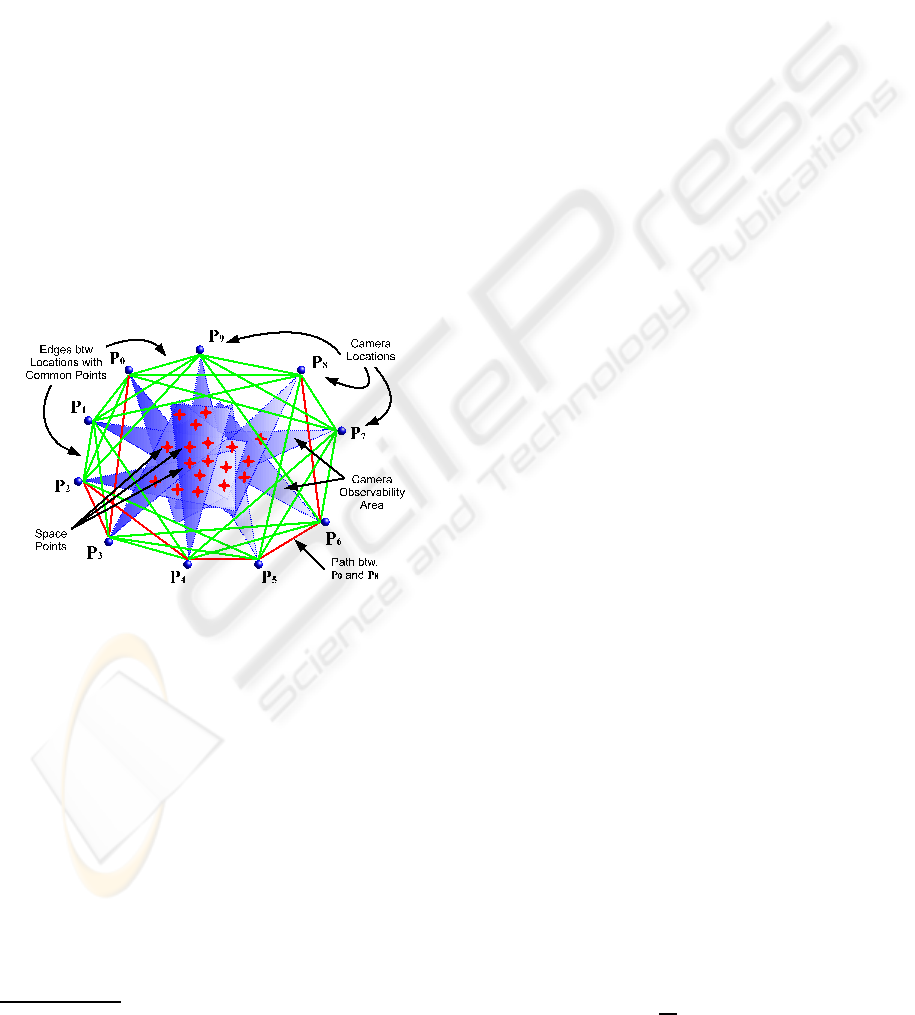
pute the external camera parameters
1
between any
two camera locations as a path of intermediate po-
sitions. Specifically, a CDG is a graph G = (V , E)
where the set of nodes V represents camera locations
and the set of edges E relates two positions whenever
the calculation of their relative movement is feasible,
i.e., when enough common points can be seen from
the two positions. Consequently, the complete move-
ment between two camera positions is a concatenation
of the intermediate displacements expressed as a path
in CDG, as shown in Figure1.
The accuracy of the results greatly depends on
how paths are selected from CDG. As mentioned
above, the recovery error is greatly dependent on the
baseline distance between successive camera loca-
tions. Besides, the amount of error also accumu-
lates and the total accuracy decreases as the number
of intermediate positions increases. Therefore, in or-
der to improve the total performance of the multiple
view calibration two main strategies can be attempted,
i.e., using locations with larger baselines and reducing
the number of intermediate positions, especially those
with worse estimates.
Figure 1: Camera-Dependency Graph (CDG). Graph of de-
pendencies where nodes are camera locations and edges
connect cameras sharing enough common points inside
their observable areas.
Our approach selects a combination of interme-
diate views that connects two camera locations with
the purpose of reducing the recovery error as much
as possible. The shortest path in a CDG where edge
weights are unreliabilities of pairwise camera motion
is chosen. Since the shortest path corresponds to the
combination having the smallest summation of unre-
liabilities and these values correlate with the error, the
resulting camera movement and 3D data will conse-
quently present a much lower amount of error com-
pared to any other feasible path.
Some additional issues must be coped with in or-
der to perform in practice such calculations. First,
1
Rotation matrix and translation vector.
an algorithm to find the shortest paths that also ful-
fil a number of conditions is necessary. A path is only
feasible if it always has enough common points visi-
ble from any three successive positions in it. This is
equivalent to the existence of positions forming trian-
gles and the whole path being triangle-connected, a
property any path in a CDG must fulfil. Besides, the
task of combining the pairwise displacements along a
path in order to attain the complete movement must
also be carefully addressed. Nonetheless, the descrip-
tion of these algorithms are out of the scope of this
paper and will not be addressed here.
4 UNRELIABILITY MEASURE
OF ESSENTIAL MATRICES
In this section we define our measure of unreliabil-
ity based on the epipolar constraint encompassed by
means of the essential matrices G that will be used
to form the weights in CDGs. Our starting point is
the approach by Kanatani (Kanatani, 1996; Kanatani,
2000), where a theoretical accuracy bound on fun-
damental matrices is described. Despite that in our
approach the fundamental matrix has been turned
into an essential matrix, yet the same theory holds
here. We basically quantify the error made in the two
processes employed to compute an estimate of the
movement parameters, namely, the renormalization
error, coping with the error during the least–squares
fitting of G, and the decomposition error, accounting
for the error carried out in the decomposition of G
into its translation vector and rotation matrix.
4.1 Renormalization Error
The uncertainty of an estimate G is measured from the
actual
¯
G by the covariance tensor V [G] = E[P ((G−
¯
G) ⊗ (G −
¯
G))P
⊤
], where E[◦] denotes expecta-
tion. The operator ⊗ stand for the tensor prod-
uct among matrices, that is, if A = (A
ij
) and B =
(B
ij
), the (ijkl) element of their tensor product is
A
ij
B
kl
. For tensors P = (P
ijkl
) and T = (T
ijkl
),
the product P T P
⊤
is a tensor whose (ijkl) element
are
∑
3
m,n,p,q=1
P
ijmn
P
klpq
T
mnpq
, whereas the (ijkl) ele-
ments of tensor P is given by P
ijkl
= δ
ij
δ
kl
−
¯
G
ij
¯
G
kl
,
being δ
ij
the Kronecker’s delta.
There exists (Kanatani, 2000) a theoretical lower
bound (TLB) on the covariance tensor V [G] which
represents an accuracy bound in the form
V [G] ≻
ε
2
N
P
S
G P
S
−
7
(1)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
116

where T ≻ S for tensors T and S means that (T − S)
is a positive semi–definite tensor, and the operation
(◦)
−
r
denotes the Moore–Penrose’s inverse of rank r.
The (ijkl) element of the tensor P
S
= (P
S
ijkl
) in Eq. (1)
is given by P
ijkl
= δ
ij
δ
kl
−(
¯
G
†
ij
¯
G
†
kl
)/k
¯
G
†
k
2
, where
¯
G
†
is the cofactor matrix of
¯
G.
On the one hand, from the renormalization step,
which employs the unbiased least–squares eigenvalue
fitting algorithm to approximate G (Kanatani, 2000),
the minimum residual J = (G
9
;G G
9
) is extracted,
providing an estimate of the squared noise level ε
2
=
J/(1− 8/N) after renormalization. G
9
is the eigen-
matrix with the smallest eigenvalue of tensor G. The
covariance tensor V [G] of the estimate G is then
V [G] =
ε
2
N
(G)
−
8
(2)
where the estimate G is computed from eigenvalues
λ
i
and eigenmatrices G
i
obtained in the renormaliza-
tion algorithm as G =
∑
8
i=1
λ
i
G
i
⊗ G
i
.
On the other hand, the Root Mean Square er-
ror (RMS) of G is defined as rms[G] = (E[kP (G−
¯
G)k
2
])
1/2
and there exists a relation between this
measure of accuracy and the covariance tensor V [G]
given by the trace of a tensor T as
rms[G] ≥
q
tr(V [G]) (3)
where tr(T ) =
∑
3
i, j=1
T
iji j
. Therefore, putting Eq. (1)
and Eq. (3) together and writing them in terms of their
eigenvalues, we obtain that
rms[G] ≥
s
ε
2
N
8
∑
i=1
1
λ
i
≥
s
ε
2
N
7
∑
i=1
1
λ
′
i
= ε
r
(4)
where λ
i
are the eigenvalues of tensor G while λ
′
i
are
these of tensor P
S
G P
S
. The renormalization error ε
r
is then defined as the lower bound in Eq.(4).
The relation between rms[G] and the TLB shows
that renormalization attains this bound when higher
order terms of noise are omitted (Kanatani, 2000).
Hence, in practice this bound is a good approximation
for the estimation of the error of the essential matrix.
Nevertheless, if any further step is involved in the ob-
taining of the movement parameters, as it is in our
case, a complementary measure is needed.
4.2 Decomposition Error
Two further steps are required to obtain the estimate
of the translation t and the rotation R from an essen-
tial matrix G. First, a geometric correction of G pre-
viously computed by renormalization to make it de-
composable into the form G = t × R. Second, the
decomposition into its movement parameters.
The first process is a Newton iteration based on
a linear approximation of the decomposability con-
straint that can be carried out up to the same level of
error attained in the renormalization. The decompo-
sition itself is a robust method that provides a transla-
tion t being the unit eigenvector of matrix GG
⊤
and
a rotation R = Vdiag(1,1,det(VU
⊤
))U
⊤
, where V
and U come from the SVD of matrix −t× G.
Remarkably, this method always provides a de-
composable solution, since R is an exact rotation ma-
trix. Furthermore, the vector t is always very close to
the valid solution. Both facts are true even if G is not
decomposable (Kanatani, 1996). Consequently, the
decomposition can be seen as an ultimate stage in the
optimal correction of the essential matrix G obtained
by renormalization, producing an improved result.
Figure 2: Decomposition Error. Symbols G
r
, G
c
, and G
d
correspond to essential matrices after renormalization, cor-
rection, and decomposition, respectively. E
G
and ε
d
stand
for recovery and decomposition errors. S
G
is the manifold
of decomposable matrices and
¯
G represents the true one.
As a way to estimate the error in the calculation of
the movement parameters E
G
, we suggest to measure
how far the matrix G is from being truly decompos-
able. Therefore, the decomposition error is defined as
ε
d
= kG
c
− G
d
k (5)
where G
c
comes from the correction and G
d
= t× R,
being t and R obtained from G
c
by decomposition.
Our claim is that the farther a matrix G is from the
decomposability constraint, the greater its decompo-
sition differs from the real one and, therefore, the less
reliable the matrix becomes, that is, if ε
d
1
≤ ε
d
2
then
E
G
1
≤ E
G
2
, as depicted in Fig.2.
4.3 Unreliability Measure
In Sec. 5.1 we show that in practice there are some
cases where there exists a clear correlation between
ε
d
and the recovery error defined as E
G
= k
¯
G− G
d
k,
where
¯
G is the true essential matrix and G
d
is the one
A NEW RELIABILITY MEASURE FOR ESSENTIAL MATRICES SUITABLE IN MULTIPLE VIEW CALIBRATION
117
obtained after decomposition. In other cases, the cor-
relation is clearer with the renormalization error ε
r
.
In order to improve the correlation with respect to
E
G
in any situation, the two previous measures are
combined in one single value called unreliability ν
G
defined as follows
ν
G
= ε
d
· ε
r
= kG
c
− G
d
k ·
s
ε
2
N
7
∑
i=1
1
λ
′
i
(6)
The value ν
G
corresponds to the weights on the
edges of CDG and the paths, representing sequences
of camera locations, will be selected to be the shortest
ones in terms of this measure of unreliability. Poste-
riorly, these paths are used to recover the complete
camera movement between to given positions. As
said, since ν
G
correlates with the recovery error E
G
and the paths thus obtained have the least possible
unreliability, it follows that the movement recovered
from these paths will have less error than other kind
of feasible paths as shown in Sec. 5.2.
5 EXPERIMENTS AND RESULTS
This section describes the data employed and the ex-
periments carried out, as well as the results obtained,
in order to show the feasibility of the CDG framework
based on the unreliability measure defined before as a
way to perform multiple view calibrations.
The goals of the experiments are, first, to establish
the correlation between the unreliability ν
G
of the es-
timated G and the recovery error E
G
so as their use
can be considered equivalent. Second, ν
G
and the
CDG derived are applied to recoverthe camera move-
ments and the 3D structure employing the sets of im-
age points from a ( generated ) sequence of locations
along a circular trajectory of the camera as data. Our
aim is to display the recovery results attained by us-
ing the shortest path in terms of the unreliability ν
G
are better than those of the usual path of consecutive
camera locations.
5.1 Description of the Data
Both the ease of obtaining a sufficient number of data
to perform a generous and varied number of experi-
ments in order to prove our claims, the ability of con-
trolling the all the setting factors and the noise levels,
as well as the necessity of having a precise ground
truth to compare our results with, have compelled us
to generate the spacial data that fit our requirements
at the first stages of our research.
The data consist of a set space points {r
α
}
α=1,...,N
randomly generated inside the region determined by
(a)
(b)
(c)
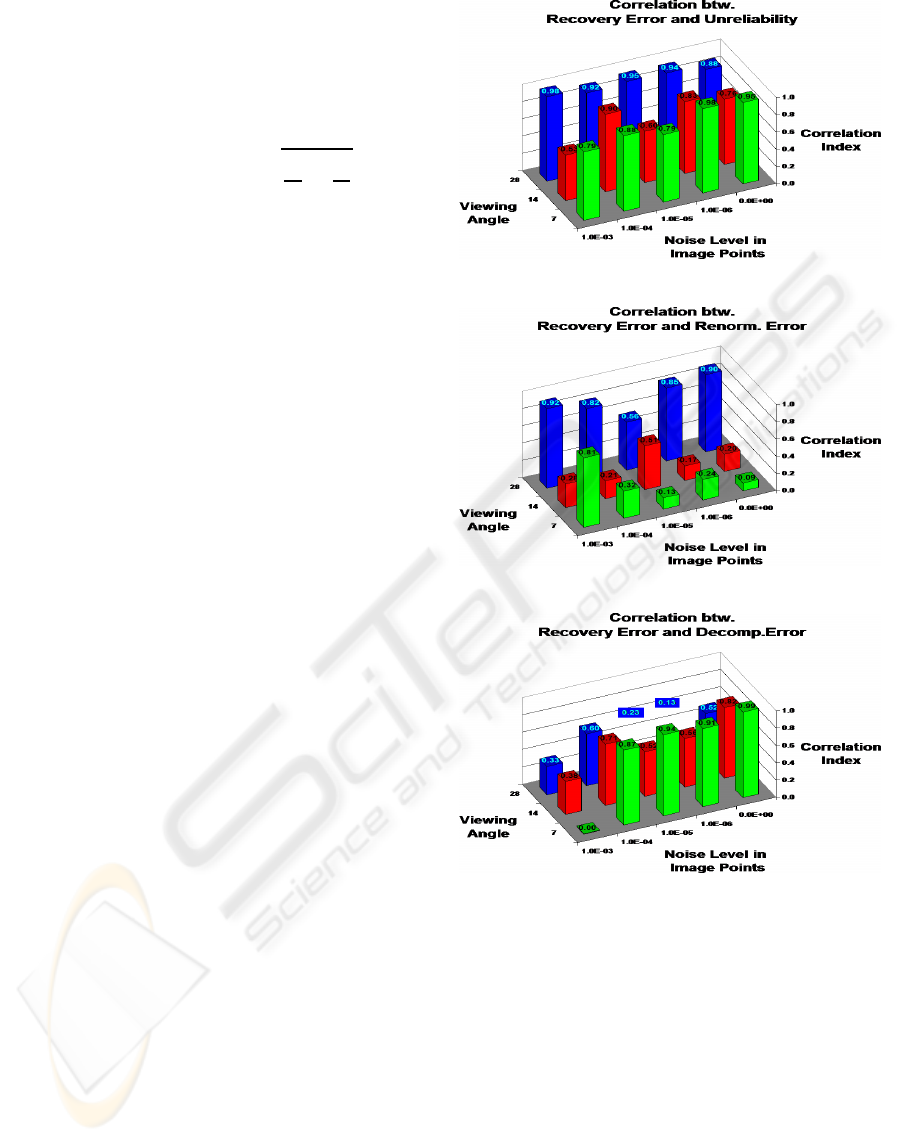
Figure 3: Experiment results (I). Correlation indices I
ρ
be-
tween recovery error E
G
and (a) unreliability ν
G
, (b) renor-
malization error ε
ren
, and (c) decomposition error ε
dec
.
two concentric spheres of radius R
max
and R
min
, re-
spectively, being R
min
= k
1
·R
max
. M camera localiza-
tions were computed in a circular trajectory around
the spheres at a distance D
cam
= k
2
· R
max
, separated
by intervals of γ
t
degrees. The orientation of the cam-
era plane is orthogonal to the radial direction.
The set of image points for each camera position
was generated projecting space points by means of
the perspective camera model and adding two kinds
of perturbations afterwards. First, the camera view-
ing angle γ
v
∈ {7
o
,14
o
,28
o
} permits to limit the po-
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
118
sitions observing the same common points. Second,
an amount of noise ε
i
∈ {0.0,10
−6
,10
−5
,10
−4
,10
−3
}
was also added to image points to simulate the error
appearing in the process of point extraction.
Constants used in the settings of each experi-
ment are N = 500, k
1
= 90%, k
2
= 3, γ = 5
o
, and
M = 360
o
/5
o
= 72, respectively. In total, there were
#{γ
v
} · #{ε
i
} = 3· 5 = 15 sets of experiments, where
image points were affected by different noise levels
and viewing angles while both 3D points and camera
localization remained constant (ground truth).
5.2 Unreliability vs. Recovery Error
In order to evaluate the suitableness of the unreliabil-
ity measure ν
G
defined in Sec. 4, for each of the pre-
vious data sets, the correlation between ν
G
and the re-
covery error E
G
was computed, along with the renor-
malization error ε
r
and the decomposition error ε
d
,
defined in Eq. (4) and Eq. (5), respectively.
Each feasible
2
pair of camera locations form an
edge e
ij
in CDG. Once the corresponding essential
matrix G
ij
for this edge and its decomposition into
corresponding t
ij
and R
ij
were obtained using the
algorithm in Sect.4, the values ν
G
ij
, ε
r
ij
, and ε
d
ij
were computed, as well as the recovery error E
ij
=
k
¯
G
ij
− G
ij
k. Notice that G
ij
= t
ij
× R
ij
.
For any viewing angle γ
v
and image noise ε
i
an
index of correlation I
ρ
was computed between error
E
G
and each one of the previous accuracy measures
– ν
G
, ε
r
, and ε
d
– as the mean value of all the par-
tial correlations {ρ
i
,i = 1,.. . ,N} obtained as follows.
A correlation ρ
i
is calculated by taking the node n
i
as the origin and employing the corresponding re-
covery error and the accuracy measures to the rest
of nodes n
j
, i 6= j, to compute a correlation coeffi-
cient. That is, if X
i
∈ { E
G
i
} and Y
i
∈ {ν
G
i
,ε
r
i
,ε
d
i
},
where E
G
i
= {E
G
ij
}, ν
G
i
= {ν
G
ij
}, ε
r
i
= {ε
r
ij
}, and
ε
d
i
= {ε
d
ij
} with j = 1,... , N, then ρ
i
= ρ(X
i
,Y
i
) =
cov(X
i
,Y
i
)/(σ
X
i
· σ
Y
i
). Indices I
ρ
as a function of γ
v
and ε
i
are plotted in Fig. 3.
The results show that the correlation index be-
tween the unreliability ν
G
and the recovery error E
G
is higher than either ε
r
or ε
d
alone. Besides, the values
of this index is pretty high and stable against noise in
the image plane and variations in the viewing angle.
Moreover, a reciprocal behaviour of ε
r
and ε
d
is ex-
hibited, that is, ε
r
presents a higher correlation when
that of ε
d
is lower, and vice versa. As a consequence
of such results, we state that the unreliability measure
ν
G
defined in Eq. (6) is a useful and robust indirect
estimate of the recovery error E
G
in general.
2
Sharing enough observable common points.
(a)
(b)
(c)
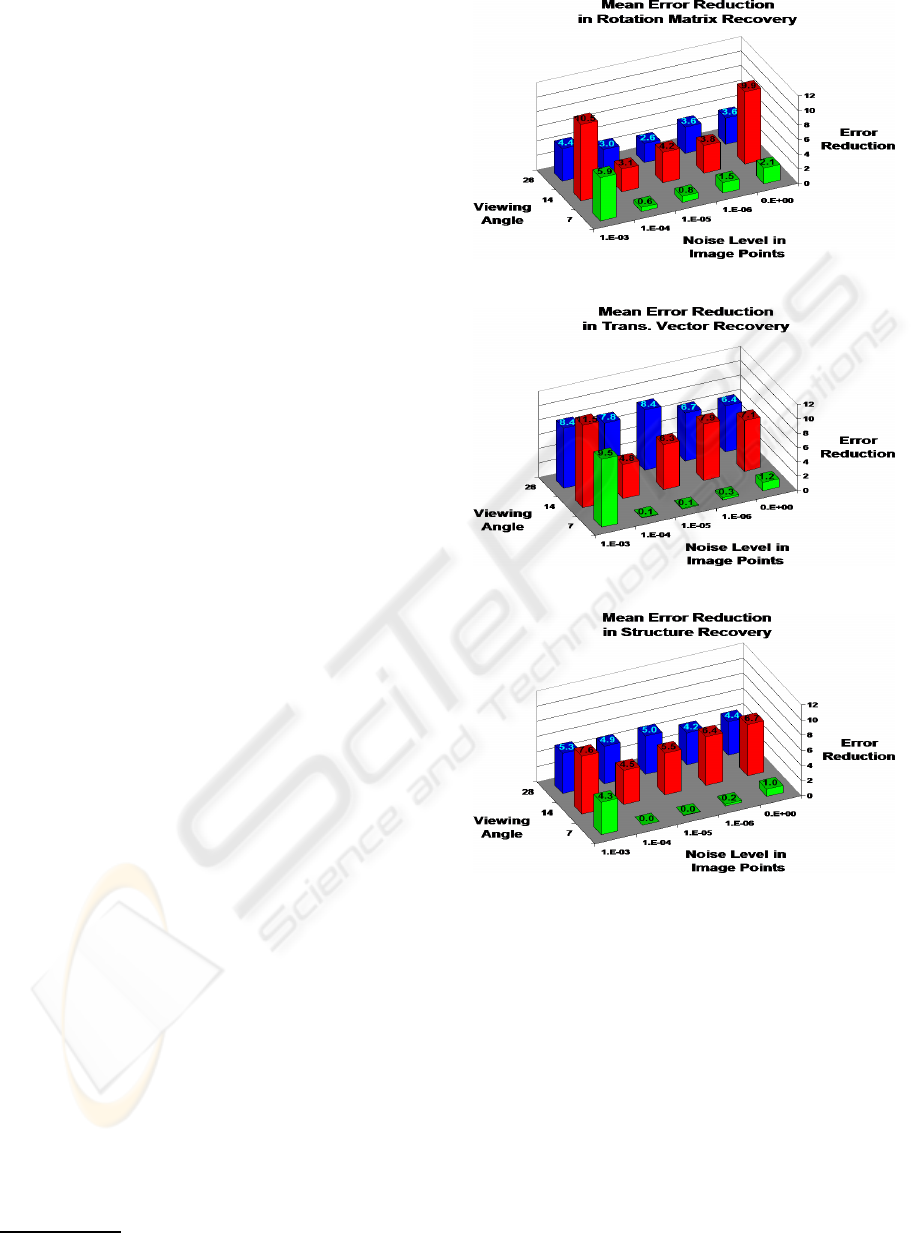
Figure 4: Experiment results (II). Mean error reduction be-
tween consecutive and the shortest paths of (a) rotation, (b)
translation, and (c) 3D reconstruction, respectively.
5.3 Shortest vs. Consecutive Paths
The objective of this section is to demonstrate the
suitability of employing the shortest path in a CDG
based on the unreliability ν
G
for recoveringthe move-
ment parameters corresponding to the camera loca-
tions along the aforementioned circular trajectory as
well as the 3D space positions of the sets of image
points. Apart from the shortest path of unreliabil-
ities ν
G
between essential matrices, the more usual
path of consecutive camera locations was also taken
A NEW RELIABILITY MEASURE FOR ESSENTIAL MATRICES SUITABLE IN MULTIPLE VIEW CALIBRATION
119
(a)
(b)
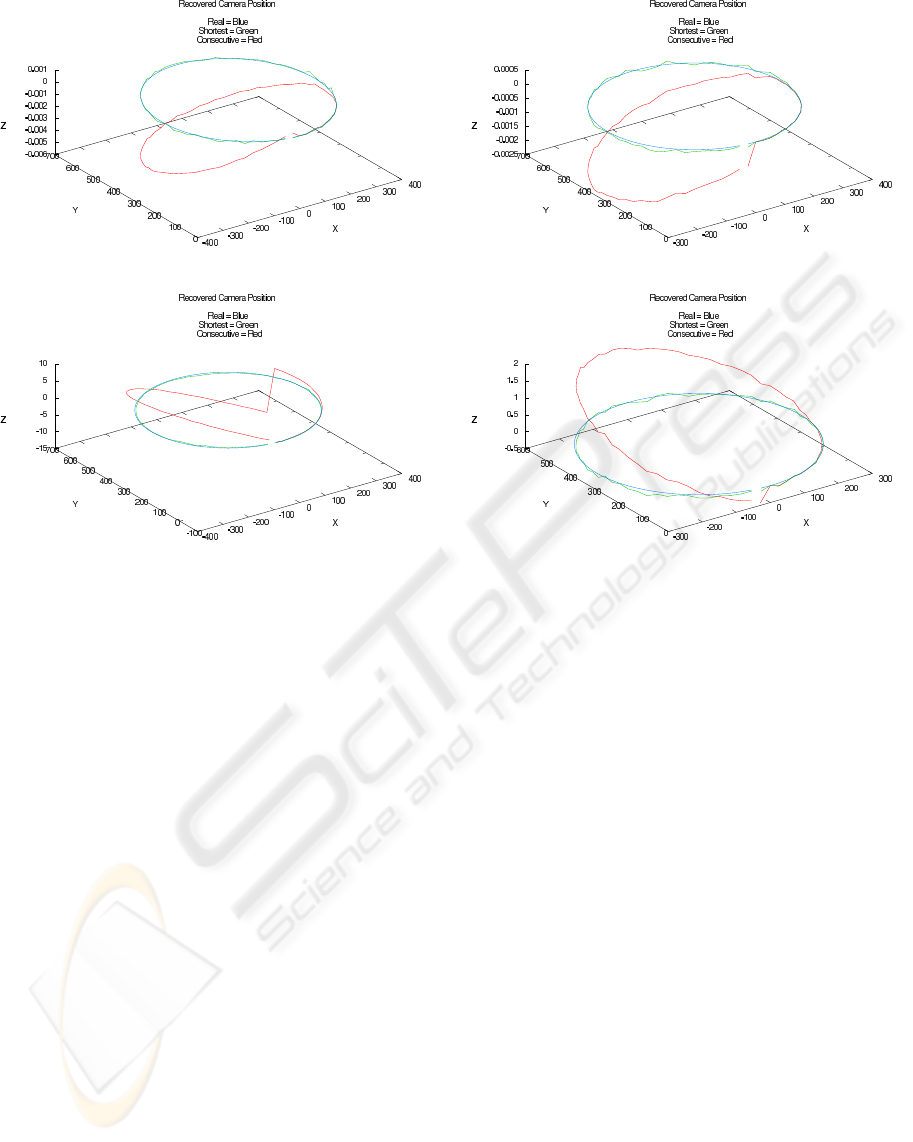
Figure 5: Some recovery results (I). Camera location in case
γ
v
= 14
o
and (a) ε
i
= 10
−6
, and (b) ε
i
= 10
−3
, respectively.
Blue lines are the true camera trajectories, while green lines
are the camera trajectory recovered using shortest paths, and
the red ones corresponds to the camera trajectory recovered
using consecutive paths. Units are pixels.
into account in such a task. The error between the
obtained results and the actual ground truth was cal-
culated afterwards in order to make comparisons. In
other words, the translation error E
t
, rotation error E
R
,
and space points error E
r
are calculated.
This process took at every step a location as the
origin and computed the set of paths to the rest of
them. The procedure was repeated then varying the
origin to cover all possible camera locations and the
mean values for all the previous error magnitudes
were computed. Fig. 4 pictures the reduction in the
amount of error when the shortest path to recover the
motion parameters was used instead of the consecu-
tive path. The error reduction was obtained dividing
the error of a consecutive path and of a shortest path
connecting the same origin and final locations.
The use of the shortest path definitely reduced the
total amount error in the calculations of both cam-
era movements ( t and R ) and 3D structure, espe-
cially when γ
v
was wider. This is because it is pos-
sible in that case to find paths which jump to more
separate locations, providing as a consequence larger
baselines that increases the accuracy. In case of nar-
(a)
(b)
Figure 6: Some recovery Results (II). Camera location in
case γ
v
= 28
o
and (a) ε
i
= 10
−6
, and (b) ε
i
= 10
−3
, re-
spectively. Blue lines are the true camera trajectories, while
green lines are the camera trajectory recovered using short-
est paths, and the red ones corresponds to the camera trajec-
tory recovered using consecutive paths. Units are pixels.
rower γ
v
, this advantage may not exist and a worse
result may appear in few cases due to some out-
lier locations, as it happens when γ
v
= 7
o
and ε
i
∈
{0.0,10
−6
,10
−5
,10
−4
}. On the other hand, if γ
v
= 7
o
and ε
i
= 10
−3
, the reduction is very big because the
consecutive path provided a very poor result.
In Fig. 5 and Fig. 6 we plot some results depicting
the shape of the actual camera trajectory along with
the two kinds of trajectories recoveredusing the short-
est paths and the consecutive paths. In both groups of
plots, we selected two instances corresponding to two
levels of image point noise, i.e., ε
i
= 10
−6
and 10
−3
.
Due to the obvious space limitations it is in fact im-
possible to show all the results obtained for all the
possible combinations of viewing angle and amount
of error in image points. Hence, only these two exam-
ples of reconstructed trajectories have been selected
to illustrate the performance of our approach.
Therefore, our aim is to display that, first, the tra-
jectories recovered using the shortest–path strategy
were substantially closer to the real one, and, second,
how the error accumulated by the consecutive path
growing as successive camera locations went farther
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
120

from the origin
3
. Moreover, it can be observed that
such an error grew accordingly to the amount of noise
added to the image points. So in Fig. 5 (a) the scale of
the error is smaller than that in Fig. 5 (b). The same
can be stated from Fig. 6 (a) and Fig. 6 (b).
It is evident that the recovered trajectory deviates
from the true one as the location goes farther from the
origin. The scale in coordinates Z is not the same as in
coordinates X and Y in order to show such deviation
and can be seen as the error in this direction since the
true value is Z = 0.0. Errors in directions X and Y
are more difficult to plot here because their sizes is
smaller compared to the range of these coordinates.
Finally, while the order of the errors produced by
consecutive paths in coordinates Z were around 10
−3
in Fig. 5 (a) and Fig. 6 (a), it was considerably larger
in Fig. 5 (b) and Fig. 6 (b), i.e., between 1 and 10,
which is around one thousand times bigger. This
is similar to the order differences in the noise level
present in the image points existing in these figures.
Consequently, whereas the error in the consecutive–
path trajectories had the same order as the image
points noise, the error of the shorted–path trajectories
was far smaller as can be seen in the depicted exam-
ples, being these trajectories really close to the ground
truth. Moreover, the viewing angle γ
v
also reduces the
error of the recovered trajectories nearly to one half
when γ
v
= 28
o
with respect to the case of γ
v
= 14
o
.
6 CONCLUSIONS
We presented in this paper a new method for multiple
view reconstruction based on the definition of an un-
reliability measure that is shown to indirectly estimate
the recovery error. Experiments exhibited a clear cor-
relation between our criterion and the error in the es-
timation of the motion parameters provided by the
essential matrix computation and decomposition into
translation and rotation. In addition to this, the con-
cept of Camera–Dependency Graph (CDG) was in-
troduced consisting of a graph where nodes represents
camera positions and edges the feasibility of comput-
ing an essential matrix between such locations.
By employing a CDG whose weights are com-
posed of the unreliability measures we could obtain
a better result for the motion parameters estimation
whenever the shortest paths in the CDG were em-
ployed rather than the usual paths of consecutive cam-
era locations. It was proven that the reduction in the
recoveryerror was larger in the case of using shortest–
path trajectories than using consecutive paths. Be-
3
Position (0.0,0.0, 0.0) in both groups of images.
sides, it was also shown by some examples how the
better performance of our approach can be appreci-
ated in the precision of the recovered trajectories.
This method can be used in applications that in-
volve dense sequences of images, like those from au-
tonomous robot navigation, estimation of camera tra-
jectories or relative position, as well as for 3D point
recovery. The future work will consist in applying this
approach to problems such as simultaneous localiza-
tion and mapping, or robot navigation, as an alterna-
tive way to increase the precision of these tasks.
ACKNOWLEDGEMENTS
The research described in this paper has been funded
by the Kankenhi No.19700188.
REFERENCES
Csurka, G., Zeller, C., Zhang, Z., and Faugeras, O. (1997).
Characterizing the uncertainty of the fundamental ma-
trix. Computer Vision and Image Understanding.
Fitzgibbon, A. W. and Zisserman, A. (1998). Automatic
camera recovery for closed or open image sequences.
In ECCV, vol. I, pp. 311-326.
Hartley, R. and Zisserman, A. (2003). Multiple view geom-
etry in computer vision. Cambridge University, 2nd
edition.
Kanatani, K. (1996). Statistical optimization for geometric
computation: Theory and Practice. North-Holland.
Kanatani, K. (2000). Optimal fundamental matrix compu-
tation: Algorithm and reliability analysis. In Proc. 6th
Symp. Sensing via Image Inf.
Longuet-Higgins, H. C. (1981). A computer algorithm for
reconstructing a scene from two projections. Nature,
293, pages 133–135.
Luong, Q.-T. and Faugeras, O. (1996). The fundamental
matrix: theory, algorithms, and stability analysis. Int.
J. Comput. Vision, 17-3.
Martinec, D. and Pajdla, T. (2006). 3d reconstruction
by gluing pair-wise euclidean reconstructions. In
3DPVT.
Martinec, D. and Pajdla, T. (San Diego, USA, 2005). 3d re-
construction by fitting low-rank matrices with missing
data. In CVPR, vol. I, pp. 198-205.
Schaffalitzky, F. and Zisserman, A. (2002). Multiview
matching for unordered image sets. In ECCV.
Sturm, P. and Triggs, B. (1996). A factorization based algo-
rithm for multi-image projective structure and motion.
In ECCV96(II), pp. 709-720.
Tomasi, C. and Kanade, T. (Nov. 1992). Shape and motion
from image streams under orthography: a factoriza-
tion method. In IJCV, 9(2): 134-154.
A NEW RELIABILITY MEASURE FOR ESSENTIAL MATRICES SUITABLE IN MULTIPLE VIEW CALIBRATION
121
