A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS

Timo Ahonen and Matti Pietik¨ainen

Machine Vision Group, University of Oulu, PL 4500, FI-90014 Oulun yliopisto, Finland

Keywords:

Local Binary Pattern, KTH-TIPS, MR8, Gabor, Texture descriptor.

Abstract:

This paper presents a new uniﬁed framework for texture descriptors such as Local Binary Patterns (LBP)

and Maximum Response 8 (MR8) that are based on histograms of local pixel neighborhood properties. This

framework is enabled by a novel ﬁlter based approach to the LBP operator which shows that it can be seen

as a special ﬁlter based texture operator. Using the proposed framework, the ﬁlters to implement LBP are

shown to be both simpler and more descriptive than MR8 or Gabor ﬁlters in the texture categorization task. It

is also shown that when the ﬁlter responses are quantized for histogram computation, codebook based vector

quantization yields slightly better results than threshold based binning at the cost of higher computational

complexity.

1 INTRODUCTION

Texture is a fundamental property of surfaces, and

automated analysis of textures has applications rang-

ing from remote sensing to document image analysis

(Tuceryan and Jain, 1998). Recent ﬁndings in apply-

ing texture methods to face image analysis, for ex-

ample, indicate that texture might have applications

in new ﬁelds of computer vision that have not been

considered texture analysis problems. Because of the

importance of texture analysis, a wide variety of dif-

ferent texture descriptors have been presented in the

literature. However, there is no formal deﬁnition of

the phenomenon of texture itself that the researchers

would agree upon. This is possibly one of the reasons

that so far no uniﬁed theory or no uniﬁed framework

of texture descriptors has been presented.

The Local Binary Pattern (LBP) (Ojala et al.,

2002), Maximum Response 8 (Varma and Zisserman,

2005) and Gabor ﬁlter based texture descriptors are

among the most studied and best known recent tex-

ture analysis techniques. Despite the large number

of publications discussing these methods, the connec-

tions and differences between them are not well un-

derstood. This paper presents a new uniﬁed frame-

work for these texture descriptors, which allows for a

systematic comparison of these widely used descrip-

tors and the parts that they are built of.

LBP is an operator for image description that is

based on the signs of differences of neighboring pix-

els. It is fast to compute and invariant to monotonic

gray-scale changes of the image. Despite being sim-

ple, it is very descriptive, which is attested by the

wide variety of different tasks it has been success-

fully applied to. The LBP histogram has proven to

be a widely applicable image feature for, e.g., texture

classiﬁcation, face analysis, video background sub-

traction, etc. (The Local Binary Pattern Bibliography,

2007).

Another frequently used approach in texture de-

scription is using distributions of quantized ﬁlter re-

sponses to characterize the texture (Leung and Malik,

2001), (Varma and Zisserman, 2005). In the ﬁeld of

texture analysis, ﬁltering and pixel value based tex-

ture operators have been seen as somewhat contradic-

tory. However, in this paper we show that the local

binary pattern operator can be seen as a ﬁlter oper-

ator based on local derivative ﬁlters at different ori-

entations and a special vector quantization function.

Apart from clarifying the connections between LBP

and ﬁlter based methods, this also helps analyzing the

properties of the LBP operator.

2 THE LOCAL BINARY PATTERN

OPERATOR

The local binary pattern operator (Ojala et al., 2002)

is a powerful means of texture description. The orig-

inal version of the operator labels the pixels of an

image by thresholding the 3x3-neighborhood of each

507

Ahonen T. and Pietikäinen M. (2008).

A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 507-512

DOI: 10.5220/0001077305070512

 SciTePress

1 1 0

1 0 0

1 2 4

163264

128

5 9 1

4 4 6

7 2 3

Threshold Weights

LBP code: 1+2+8+64+128=203

Figure 1: The basic LBP operator.

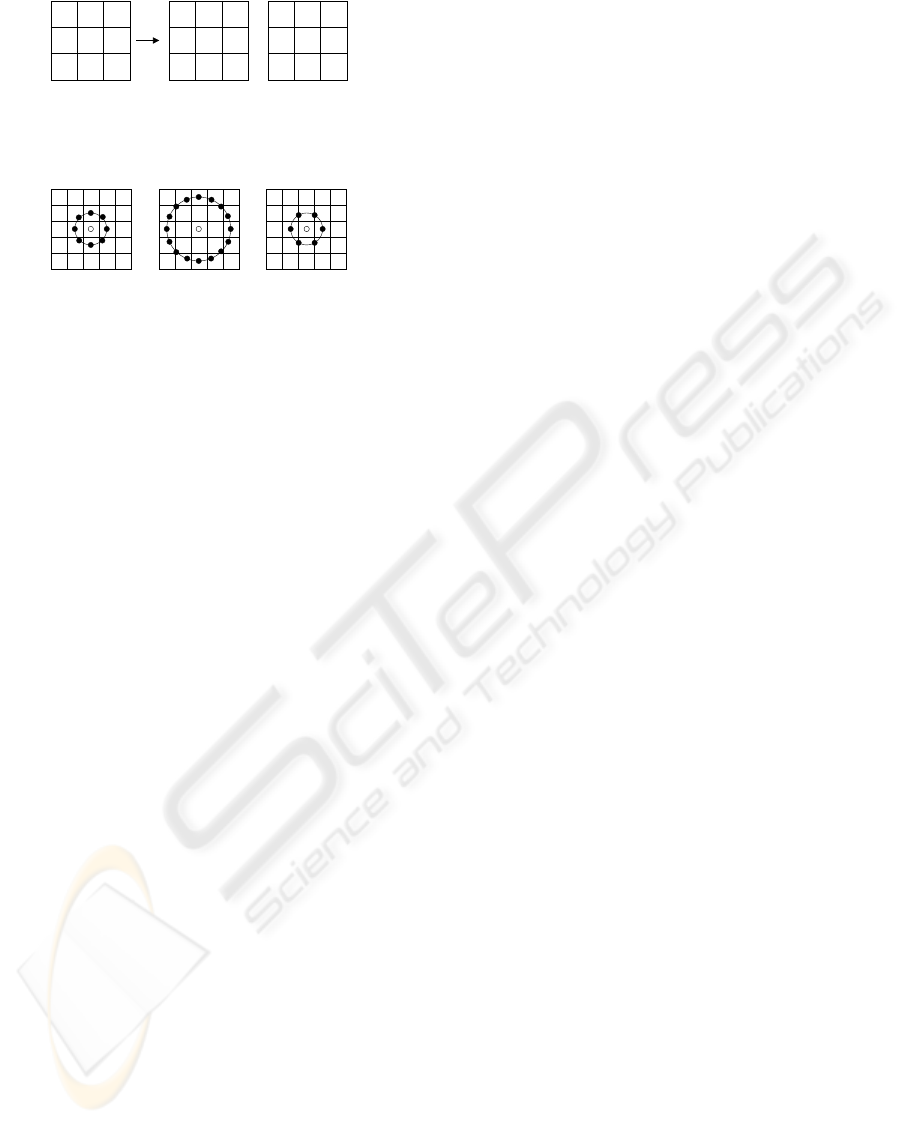
Figure 2: Three circular neighborhoods: (8,1), (16,2), (6,1).

The pixel values are bilinearly interpolated whenever the

sampling point is not in the center of a pixel.

pixel with the center value and summing the thresh-

olded values weighted by powers of two. Then the

histogram of the labels can be used as a texture de-

scriptor. See Fig. 1 for an illustration of the basic

LBP operator.

The operator can also be extended to use neigh-

borhoods of different sizes (Ojala et al., 2002). Us-

ing circular neighborhoods and bilinearly interpolat-

ing the pixel values allow any radius and number of

pixels in the neighborhood. For neighborhoods we

will use the notation (P, R) which means P sampling

points on a circle of radius of R. See Fig. 2 for an

example of different circular neighborhoods.

3 FRAMEWORK FOR FILTER

BANK AND VECTOR

QUANTIZATION BASED

TEXTURE DESCRIPTORS

Apart from LBP and other similar methods work-

ing directly on pixel values, another widely used ap-

proach to texture analysis is to convolve an image

with N different ﬁlters whose responses at a certain

position (x,y) form an N-dimensional vector. At

learning stage, a set of such vectors is collected from

training images and the set is clustered using, e.g.,

k-means to form a codebook. Then each pixel of a

texture image is labeled with the label of the nearest

cluster center and the histogram of these labels over a

texture image is used to describe the texture. (Leung

and Malik, 2001), (Varma and Zisserman, 2005).

More formally, let I(x, y) be the image to be de-

scribed by the texture operator. Now the vector val-

ued image obtained by convolving the original image

with ﬁlter kernels is

(x, y) =







(x, y) = I(x, y) ⋆ F







(1)

The labeled image I

lab

(x, y) is obtained with a vector

quantizer f : R

7→ {0, 1, 2, ··· , M − 1}, where M is

the number of different labels produced by the quan-

tizer. Thus, the labeled image is

lab

(x, y) = f(I

(x, y)) (2)

and the histogram of labels is

∑

x,y

δ{i, I

lab

(x, y)}, i = 0, . . . , M − 1, (3)

in which δ is the Kronecker delta.

If the task is classiﬁcation or categorization as in

this work, several possibilities exist for classiﬁer se-

lection. The most typical strategy is to use nearest

neighbor classiﬁer using, e.g., χ

distance to measure

the distance between histograms (Leung and Malik,

2001), (Varma and Zisserman, 2005). In (Varma and

Zisserman, 2004), the nearest neighbor classiﬁer was

compared to Bayesian classiﬁcation but no signiﬁcant

difference in the performance was found. In (Caputo

et al., 2005) it was shown that the performance of

a material categorization system can be boosted by

using suitably trained support vector machine based

classiﬁer. In this work, the main interest is not in the

classiﬁer design but in the local descriptors and thus

the nearest neighbor classiﬁer with χ

distance was

selected for the experimental part.

In the following two subsections we take a look

at the two main parts of the proposed texture descrip-

tion framework, the ﬁlter bank and the quantization

method.

3.1 Filter Bank

In this paper we compare three different types of ﬁl-

ter kernels that are used in texture description. The

ﬁrst ﬁlter bank is a set of oriented derivative ﬁlters

whose thresholded output is shown to be equivalent

to the local binary pattern operator. The other two ﬁl-

ter banks included in the comparison are Gabor ﬁlters

and Maximum Response 8 ﬁlter set.

A novel way to look at the LBP operator proposed

in this paper is to see it as a special ﬁlter-based texture

operator. The ﬁlters for implementing LBP are ap-

proximations of image derivatives computed at differ-

ent orientations. The ﬁlter coefﬁcients are computed

so that they are equal to the weights of bilinear inter-

polation of pixel values at sampling points of the LBP

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

508

0 0 0

−1

0 0 0

−1

0 −0.914 0.207

0.207 0.5

Figure 3: Filters F

···F

of the total of 8 local derivative

ﬁlters at (8,1) neighborhood. The remaining 5 ﬁlters are

obtained by mirroring the ﬁlters shown here.

operator and the coefﬁcient at ﬁlter center is obtained

by subtracting 1 from the center value. For example,

the kernels shown in Fig. 3 can be used for ﬁlter based

implementation of local binary pattern operator in the

circular (8,1) neighborhood. The response of such

ﬁlter at location (x, y) gives the signed difference of

the center pixel and the sampling point corresponding

to the ﬁlter. These ﬁlters, which will be called local

derivative ﬁlters in the following, can be constructed

for any radius and any number of sampling points.

Another type of ﬁlter kernels that is widely used

in texture description is Gabor ﬁlters, which are com-

plex ﬁlters whose spatial representation is obtained

by multiplying a Gaussian with a complex sinusoid.

The typical way Gabor ﬁlters are applied in texture

description is to convolve the input image with a bank

of Gabor ﬁlters and compute a set of features from the

output images. A lot of work has been devoted to de-

signing the ﬁlter bank and feature computation meth-

ods, see, e.g., (Manjunath and Ma, 1996), (Clausi and

Jernigan, 2000), (Grigorescu et al., 2002). In this

work we apply the Gabor ﬁlters in the proposed tex-

ture description framework, i.e. the responses of the

ﬁlter bank at a certain position are stacked into a vec-

tor which is used as an input for the vector quantizer.

The third considered ﬁlter bank is the Maximum

Response 8 bank (Varma and Zisserman, 2005). That

ﬁlter set consists of 38 ﬁlters: two isotropic ﬁlters

(Gaussian and Laplacian of Gaussian) and an edge

and a bar ﬁlter both at 3 scales and 6 orientations.

As an intermediate step between ﬁltering and vector

quantization, the maximum of the 6 responses at dif-

ferent orientations is computed which results in a to-

tal of 8 responses. In the proposed uniﬁed framework

this maximum selection falls more conveniently into

the vector quantization operation and it is discussed

in more detail in the next subsection.

3.2 Vector Quantization

The assumption onto which the proposed texture de-

scription framework is based on is that the joint dis-

tribution of ﬁlter responses can be used to describe

the image texture. Depending on the size of the ﬁl-

ter bank, the dimension of the vectors in the image

(x, y) can be high and quantization of the vectors is

needed for reliable estimation of the histogram.

A simple, non-adaptive way to quantize the ﬁlter

responses is to threshold them and to compute the sum

of thresholded values multiplied by powers of two:

lab

(x, y) =

∑

n=1

s{I

(x, y)}2

n−1

, (4)

where s(z) is the thresholding function

s{z} =



1, z ≥ 0

0, z < 0

(5)

Thresholding divides each dimension of the ﬁlter

bank output into two bins. The total number of dif-

ferent labels produced by threshold quantization is 2

where N is the number of ﬁlters.

Now, if the ﬁlter bank that was used to obtain the

image I

(x, y) is the set of local derivative ﬁlters (e.g.

the ﬁlters presented in Fig. 3), the ﬁlter responses

are equal to the signed differences of the pixel I(x, y)

and its neighbors. As the quantizer (4) is applied to

(x, y), the resulting labels are equal to those ob-

tained with the local binary pattern operator using the

same neighborhood. Therefore, the LBP operator can

be represented in the proposed framework.

Another method for quantizing the ﬁlter responses

is to construct a codebook of them at the learning

stage and then use the nearest codeword to represent

the ﬁlter bank output at each location:

lab

(x, y) = argmin



(x, y) − c



, (6)

in which c

is the m-th vector (codeword) in the code-

book. This approach is used in (Leung and Malik,

2001) and (Varma and Zisserman, 2005), which use

k-means to construct the codebook whose elements

are called textons. Codebook based quantization of

signed differences of neighboring pixels (which cor-

respond to local derivative ﬁlter outputs) was pre-

sented in (Ojala et al., 2001).

When comparing these two methods for quantiz-

ing the ﬁlter responses, one might expect that the

if the number of labels produced by the quantizers

is kept roughly the same, the codebook based quan-

tizer handles the possible statistical dependencies be-

tween the ﬁlter responses better. On the other hand,

since the codebook based quantization requires the

search for the closest codeword at each pixel loca-

tion, it is clearly slower than simple thresholding,

even though a number of both exact and approximate

techniques have been proposed for ﬁnding the near-

est codeword without exhaustive search through the

codebook (Gray and Neuhoff, 1998, p. 2362).

A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS

509

It is important to note that a clever co-design of the

ﬁlter bank and the vector quantizer can also make the

texture descriptor rotationally invariant. Again, two

different strategies have been proposed. Rotationally

invariant LBP codes are obtained by circularly shift-

ing a LBP binary code to its minimum value (Ojala

et al., 2002). In the joint framework this can be rep-

resented as further combining the labels of threshold

quantization (4) so that all the different labels that can

arise from rotations of the local gray pattern are joined

to form a single label.

On the other hand, the approach chosen for the

MR8 descriptor to achieve rotational invariance is to

select only the maximum of the 6 different rotations

of each bar and edge ﬁlters. Only these maximum

values and the responses of the two isotropic ﬁlters

are used in further quantization so the 8-dimensional

response of the ﬁlter is invariant to rotations of the

gray pattern.

4 EXPERIMENTS

To test the proposed framework and to systemati-

cally explore the relative descriptiveness of the differ-

ent ﬁlter banks and vector quantization methods, the

challenging task of material categorization using the

KTH-TIPS2 database (Mallikarjuna et al., 2006) was

utilized.

4.1 Experimental Setup

The KTH-TIPS2 database contains 4 samples of 11

different materials, each sample imaged at 9 different

scales and 12 lighting and pose setups, totaling 4572

images.

Caputo et al. performed material categorization

tests using the KTH-TIPS2 and considered especially

the signiﬁcance of classiﬁer selection (Caputo et al.,

2005). In that paper, the main conclusions were that

the state-of-the-art descriptors such as LBP and MR8

have relatively small differences in the performance

but signiﬁcant gains in classiﬁcation rate can be ob-

tained by using support vector machine classiﬁer in-

stead of nearest neighbor. Moreover, the classiﬁca-

tion rates can be enhanced by increasing the number

of samples used for training.

In this work, the main interest is to examine the

relative descriptiveness of different setups of the ﬁlter

bank based texture descriptors. To facilitate this task,

we chose the most difﬁcult test setup used in (Caputo

et al., 2005), namely using the nearest neighbor clas-

siﬁer with only one sample (i.e. 9*12 images) per

material class for training.

Table 1: Properties of the tested ﬁlter kernels.

Filter bank Size Num of ﬁlters

Local der. ﬁlters 3× 3 8

Gabor(1,4) 7× 7 8

Gabor(4,6) 49× 49 48

MR8 49× 49 38

16 32 64 128 256

0.4

0.42

0.44

0.46

0.48

0.5

0.52

0.54

0.56

0.58

0.6

Local derivatives

Gabor(4,6)

Gabor(1,4)

MR8

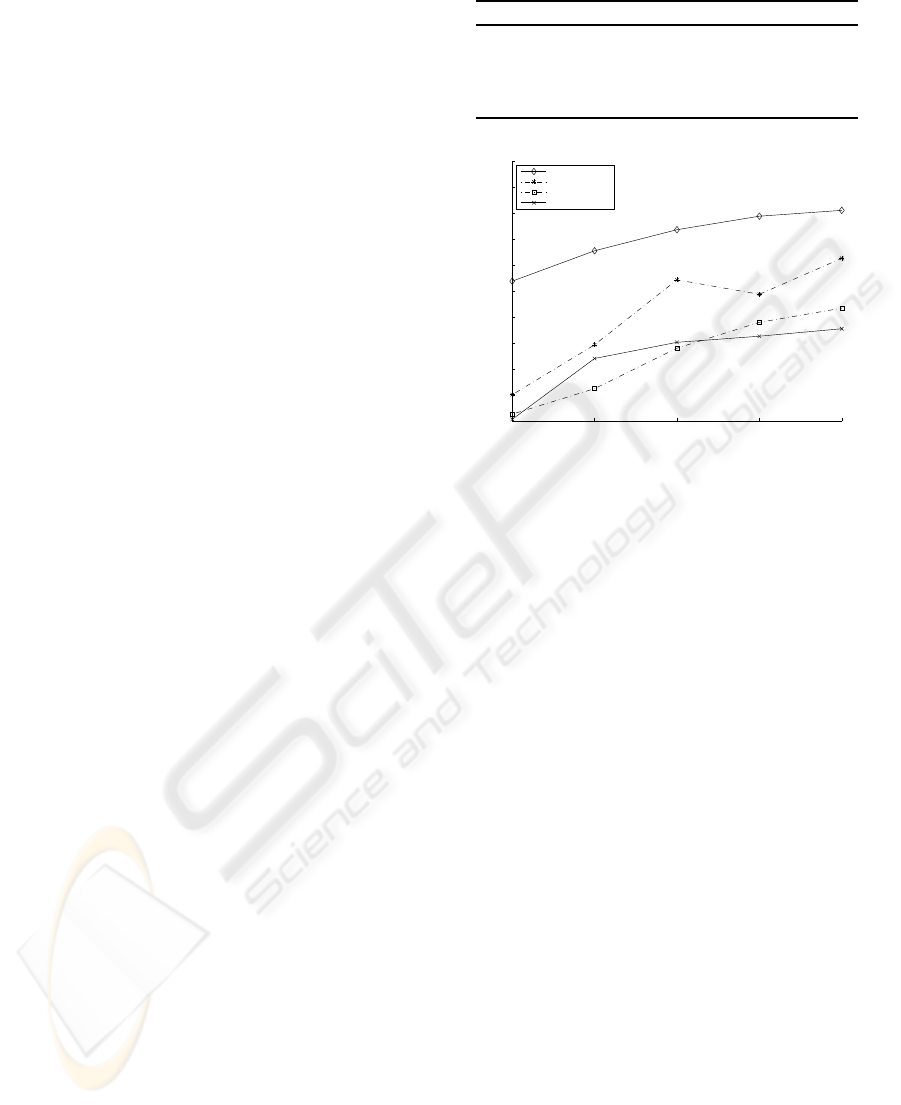
Figure 4: The categorization rates for different ﬁlter banks

as a function of codebook size

The proposed framework allowed testing the per-

formance of different ﬁlters and different quantization

methods independently. The ﬁlter banks that were in-

cluded in the test were local derivative ﬁlters, two dif-

ferent banks of Gabor ﬁlters and MR8 ﬁlters. The

local derivative ﬁlter bank was chosen to match the

LBP

8,1

operator which resulted in 8 ﬁlters (see Fig.

3). Two very different types of Gabor were tested, one

with only 1 scale and 4 orientations and small spatial

support (7 × 7) and another one with 4 scales and 6

orientations and larger spatial support. The properties

of the tested ﬁlter kernels are listed in table 1.

4.2 Codebook based Vector

Quantization

All the 4 ﬁlter banks were tested using two types

of vector quantization: thresholding and codebook

based quantization. For codebook based quantization,

the selected approach was to aim for compact, univer-

sal texton codebooks, i.e. codebooks of rather small

size that are not tailored for this speciﬁc set of tex-

tures. Therefore, the KTH-TIPS1 database (Mallikar-

juna et al., 2006) was used to learn the codebooks.

That database is similar to KTH-TIPS2 in terms of

imaging conditions but it contains partly different set

of materials (textures). The codebook sizes that were

tested were 32. . . 256 codewords.

The categorization rates as a function of the code-

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

510

Table 2: Recognition rates for different ﬁlter banks and

quantization methods.

Codebook Thresholding

Local der. ﬁlters 0.562 0.532

Gabor(1,4) ﬁlters 0.487 0.383

Gabor(4,6) 0.525 -

MR8 ﬁlters 0.471 0.498

book size obtained with each ﬁlter bank and code-

book based quantization is plotted in Figure 4. The

ﬁgure shows that for most of the time, using a larger

codebook enhances the categorization rate but the se-

lection of the ﬁlter bank is a more dominant factor

than the codebook size. For example, local deriva-

tive ﬁlters achieve a higher categorization rate with

the smallest codebook size than the MR8 ﬁlters with

any codebook size.

4.3 Thresholding based Vector

Quantization

In the next experiment the material categorization

tests were performed using the same ﬁlter banks but

thresholding based vector quantization. The local

derivative and Gabor ﬁlters have zero mean, thus the

thresholding function (5) was applied directly. For

the edge and bar ﬁlters in the MR8 ﬁlter set, only the

maximum of responses over different orientations is

measured and therefore in that case the mean of 8-

dimensional response vectors over all the training im-

ages was computed and subtracted from the response

before applying thresholding.

Table 2 lists the categorization rates using thresh-

olding based quantization and the maximum cate-

gorization rate over different codebook sizes for the

four tested ﬁlter banks. The Gabor(4,6) ﬁlter bank

was omitted from this experiment due to the large

number of ﬁlters in the ﬁlter bank (the resulting his-

tograms would have been of length 2

). Codebook

based quantization yields slightly better categoriza-

tion rate than thresholding when using local derivative

ﬁlters. With the Gabor(1,4) ﬁlter bank thresholding

performs much worse than codebook based quantiza-

tion, but interestingly with MR8 ﬁlters, thresholding

yields better rate.

To conclude the performed experiments, the lo-

cal derivative ﬁlters give the best categorization rate

over the tested ﬁlter sets with both quantization func-

tions. The results obtained in these experiments also

attest those presented in (Ojala et al., 2001) which

showed that codebook based quantization of signed

gray-level differences yields slightly better recogni-

tion than LBPs, however at the cost of higher compu-

tational complexity. Considering the computational

cost of the presented methods, thresholding based

quantization is much faster than codebook based

quantization. As for the ﬁlter bank operations, the

computational cost grows with the size and number

of ﬁlters, but using FFT based convolution can make

the operations faster. Still, at two extremes, the com-

putations for local derivative ﬁlter and thresholding

based labeling of an image of size of 256 × 256 take

0.04 seconds whereas the codebook based labeling

of the same image using Gabor(4,6) ﬁlters (and per-

forming convolutions using FFT) take 10.98 seconds.

Both running times were measured using unoptimized

Matlab implementations of the methods on a PC with

AMD Athlon 2200 MHz processor.

4.4 Filter Subset Selection

The third experiment tested whether it is possible to

select a representative subset of ﬁlters from a large

ﬁlter bank for thresholding based quantization. The

number of labels produced by the quantizer is 2

which N is the number of ﬁlters, which means that

the length of the label histograms grows exponentially

with respect to the number of ﬁlters. Thus a small ﬁl-

ter bank is desirable for the thresholding quantization.

In this experiment, the Sequential Floating For-

ward Selection (SFFS) (Pudil et al., 1994) algorithm

was used to select a maximum of 8 ﬁlters from a larger

ﬁlter bank. The optimization criterion was the recog-

nition rate over the training set (KTH-TIPS1). Two

different initial ﬁlter banks were tested. First, 8 ﬁlters

were selected from the 48 ﬁlters in the Gabor(4,6) ﬁl-

ter bank. However, the resulting 8-ﬁlter bank did not

perform well on the testing database, yielding a cate-

gorization rate of only 0.295.

In the face recognition literature, there are ﬁndings

that LBP and Gabor ﬁlter based information are com-

plementary. In (Yan et al., 2007), score level fusion

of LBP and Gabor ﬁlter based similarity scores was

done. Motivated by these ﬁndings, SFFS was used to

select 8 ﬁlters from the union of local derivative and

Gabor(1,4) ﬁlter banks. This resulted in a set of 6

local derivative and 2 Gabor ﬁlters and the resulting

ﬁlter bank reached categorization rate of 0.544 which

is signiﬁcantly higher than the rate of Gabor(1,4) ﬁl-

ter bank and slightly higher than the rate of the local

derivative ﬁlter bank.

A FRAMEWORK FOR ANALYZING TEXTURE DESCRIPTORS

511

5 DISCUSSION AND

CONCLUSIONS

In this paper we have presented a novel uniﬁed frame-

work under which the histogram based texture de-

scription methods such as local binary pattern and

MR8 descriptors can be explained and analyzed. This

framework allows for systematic comparison of dif-

ferent texture descriptors and the parts that the de-

scriptors are built of. Such novel approach can be

useful in analyzing texture descriptors since they are

usually presented as a sequence of steps whose rela-

tion to other texture description methods is unclear.

The framework presented in this work allows for ex-

plicitly illustrating the connection between the parts

of the LBP and MR8 descriptors and experimenting

with the performance of each part.

The ﬁlter sets and vector quantization techniques

for LBP, MR8 and Gabor ﬁlter based texture descrip-

tors were compared in the this paper. In this com-

parison it was found out that the local derivative ﬁl-

ter responses are both fastest to compute and most

descriptive. This somewhat surprising result further

attests the previous ﬁndings that texture descriptors

relying on small-scale pixel relations yield compara-

ble or even superior results to those based on ﬁlters of

larger spatial support (Ojala et al., 2002), (Varma and

Zisserman, 2003).

When comparing the different vector quantization

methods, codebook based quantization was discov-

ered to be slightly more descriptive than thresholding

in most cases. Finally, the preliminary experiments on

combining local derivative and Gabor ﬁlter responses

showed that these ﬁlter sets may be complementary

and may yield better performance than either of the

sets alone.

Not only does the presented framework contribute

to understanding and comparison of existing texture

descriptors but it can be utilized for more systematic

development of new, even better performing meth-

ods. The framework is simple to implement and to-

gether with the publicly available KTH-TIPS2 image

database it can be easily used for comparing novel

descriptors with the current state-of-the-art methods.

We believe that further advances in both the ﬁlter bank

and vector quantizer design are possible, especially as

new invariance properties of the descriptors are aimed

for.

REFERENCES

Caputo, B., Hayman, E., and Mallikarjuna, P. (2005). Class-

speciﬁc material categorisation. In Proc. ICCV 2005,

pages 1597–1604.

Clausi, D. A. and Jernigan, M. E. (2000). Designing Gabor

ﬁlters for optimal texture separability. Pattern Recog-

nition, 33(11):1835–1849.

Gray, R. M. and Neuhoff, D. L. (1998). Quantization. IEEE

Trans. Image Process, 44(6):2325–2383.

Grigorescu, S. E., Petkov, N., and Kruizinga, P. (2002).

Comparison of texture features based on Gabor ﬁlters.

IEEE Trans. Image Process., 11(10):1160–1167.

Leung, T. and Malik, J. (2001). Representing and recog-

nizing the visual appearance of materials using three-

dimensional textons. Int. J. Comput. Vision, 43(1):29–

44.

Mallikarjuna, P., Fritz, M., Targhi, A. T., Hayman,

E., Caputo, B., and Eklundh, J.-O. (2006).

The KTH-TIPS and KTH-TIPS2 databases.

http://www.nada.kth.se/cvap/databases/kth-tips/.

Manjunath, B. S. and Ma, W.-Y. (1996). Texture features

for browsing and retrieval of image data. IEEE Trans.

Pattern Anal. Mach. Intell., 18(8):837–842.

Ojala, T., Pietik¨ainen, M., and M¨aenp¨a¨a, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. IEEE Trans.

Pattern Anal. Mach. Intell., 24(7):971–987.

Ojala, T., Valkealahti, K., Oja, E., and Pietik¨ainen, M.

(2001). Texture discrimination with multidimensional

distributions of signed gray-level differences. Pattern

Recognition, 34(3):727–739.

Pudil, P., Novovicov´a, J., and Kittler, J. (1994). Floating

search methods in feature selection. Pattern Recogni-

tion Letters, 15(10):1119–1125.

The Local Binary Pattern Bibliography (2007).

http://www.ee.oulu.ﬁ/mvg/page/lbp bibliography.

Tuceryan, M. and Jain, A. K. (1998). Texture analysis. In

Chen, C. H., Pau, L. F., and Wang, P. S. P., editors,

The Handbook of Pattern Recognition and Computer

Vision (2nd Edition), pages 207–248. World Scientiﬁc

Publishing Co.

Varma, M. and Zisserman, A. (2003). Texture classiﬁcation:

Are ﬁlter banks necessary? In Proc. CVPR 2003, vol-

ume 2, pages 691–698.

Varma, M. and Zisserman, A. (2004). Unifying statistical

texture classiﬁcation frameworks. Image Vision Com-

put., 22(14):1175–1183.

Varma, M. and Zisserman, A. (2005). A statistical approach

to texture classiﬁcation from single images. Interna-

tional Journal of Computer Vision, 62(1–2):61–81.

Yan, S., Wang, H., Tang, X., and Huang, T. S. (2007). Ex-

ploring feature descriptors for face recognition. In

Proc. ICASSP 2007.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

512