
LEARNING A WARPED SUBSPACE MODEL OF FACES WITH
IMAGES OF UNKNOWN POSE AND ILLUMINATION
Jihun Hamm and Daniel D. Lee
GRASP Laboratory, University of Pennsylvania, 3330 Walnut Street, Philadelphia, PA, USA
Keywords:
Image-based modeling, probabilistic generative model, illumination subspace, super-resolution, MAP estima-
tion, multiscale image registration.
Abstract:
In this paper we tackle the problem of learning the appearances of a person’s face from images with both
unknown pose and illumination. The unknown, simultaneous change in pose and illumination makes it difficult
to learn 3D face models from data without manual labeling and tracking of features. In comparison, image-
based models do not require geometric knowledge of faces but only the statistics of data itself, and therefore
are easier to train with images with such variations. We take an image-based approach to the problem and
propose a generative model of a warped illumination subspace. Image variations due to illumination change are
accounted for by a low-dimensional linear subspace, whereas variations due to pose change are approximated
by a geometric warping of images in the subspace. We demonstrate that this model can be efficiently learned
via MAP estimation and multiscale registration techniques. With this learned warped subspace we can jointly
estimate the pose and the lighting conditions of test images and improve recognition of faces under novel
poses and illuminations. We test our algorithm with synthetic faces and real images from the CMU PIE and
Yale face databases. The results show improvements in prediction and recognition performance compared to
other standard methods.
1 INTRODUCTION
We tackle the problem of learning generative mod-
els of a person’s face from images with both un-
known pose and illumination. The appearance of a
person’s face undergoes large variations as illumina-
tion and viewing directions change. A full 3D model
of a face allows us to synthesize images at arbitrary
poses and illumination conditions. However, learn-
ing such a 3D model from images alone is very dif-
ficult since it requires that feature correspondences
are known accurately, even under dramatic lighting
changes. In this paper we develop an image-based
approach, which does not use 3D models nor solve
correspondence problems, but instead directly learns
the statistical properties of images under pose and il-
lumination variations. (see Fig. 1).
One of the simplest image-based models of faces
is an Eigenface model (Turk and Pentland, 1991),
which models data as an affine subspace in the space
of pixel intensities. Although Eigenfaces were origi-
nally applied to image variations across different peo-
Figure 1: Typical unlabeled images with both varying pose
and illumination conditions make it difficult to learn 3D
structures directly from sample images. We aim to learn
an appearance model of a person’s face given such im-
ages without finding, labeling and tracking features between
frames.
ple, a subspace model can explain the illumination
variation of a single person exceptionally well (Halli-
nan, 1994; Epstein et al., 1995). The so-called illumi-
nation subspace has been thoroughly studied theoret-
ically (Ramamoorthi, 2002; Basri and Jacobs, 2003).
However, such a linear subspace model cannot cope
with the simultaneous nonlinear change of poses.
On the other hand, suppose we are given multiple-
pose views of a face under a fixed lighting condition.
219
Hamm J. and D. Lee D. (2008).
LEARNING A WARPED SUBSPACE MODEL OF FACES WITH IMAGES OF UNKNOWN POSE AND ILLUMINATION.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 219-226
DOI: 10.5220/0001076502190226
Copyright
c
SciTePress
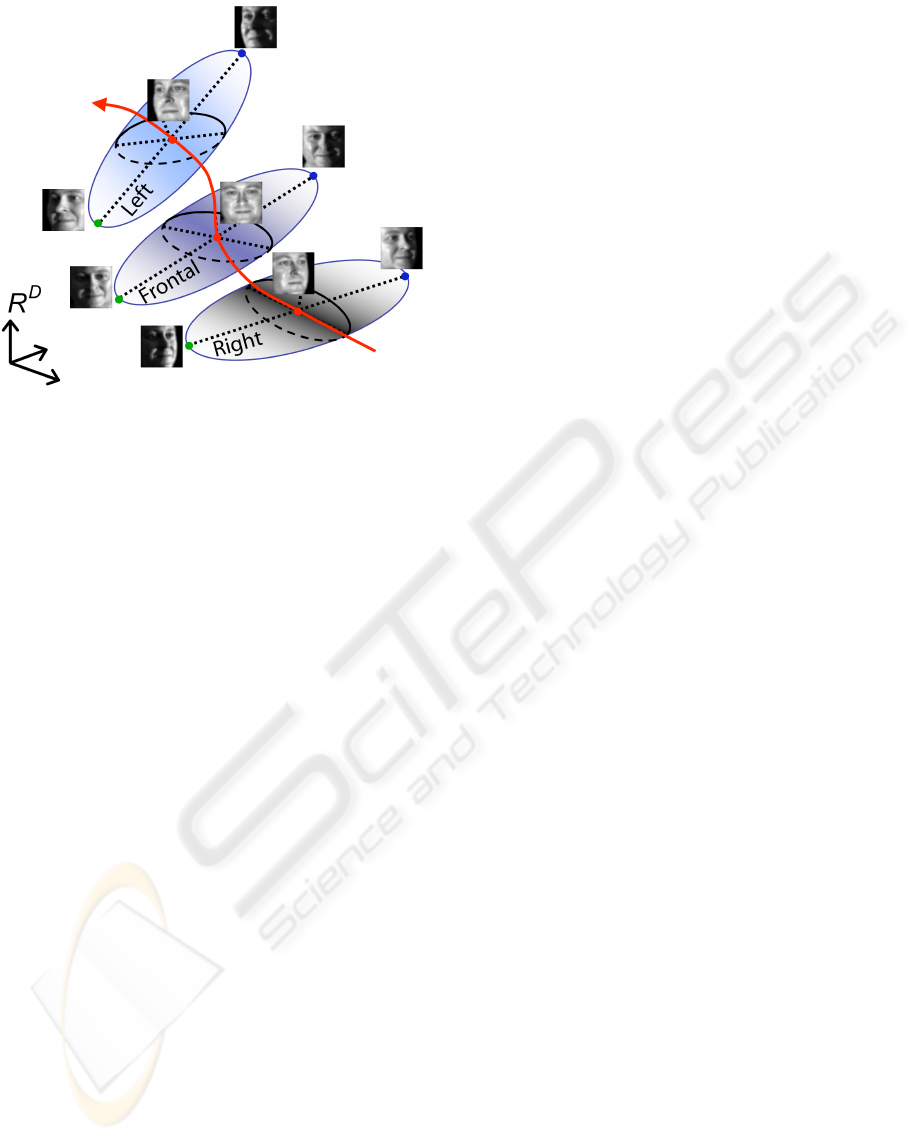
Figure 2: A probabilistic model of pose and illumination
variations. The ellipsoid in the middle represents frontal
images with all possible illuminations, lying closely on a
low-dimensional subspace. As the viewpoint changes from
a right-profile to a left-profile pose, the ellipsoid is trans-
ported continuously along a nonlinear manifold. We model
this nonlinear variation with a geometric warping of images.
If the pose change is moderate, we can learn a gen-
erative model by geometrically registering the multi-
view images and probabilistically combining them to
estimate the unknown latent image. Such generative
models have been proposed for the super-resolution
problem (Hardie et al., 1997; Tipping and Bishop,
2002; Capel and Zisserman, 2003). However, previ-
ous work considers only a single latent image rather
than a latent subspace, and therefore can handle only
one-dimensional illumination changes and not the full
range of illumination variations from arbitrary light
sources.
In this paper we model the simultaneous change
of pose and illumination of a person’s face by a
novel “warped subspace model.” Image variations
due to illumination change at a fixed pose are cap-
tured by a low-dimensional illumination subspace;
and variations due to pose change are approximated
by a geometric warping of images in the subspace.
A schematic of the warped subspace is depicted in
Fig. 2.
1.1 Related Work
Image-based models of faces have been proposed be-
fore. A popular multi-pose representation of images
is the light-field presentation, which models the radi-
ance of light as a function of the 5D pose of the ob-
server (Gross et al., 2002a; Gross et al., 2002b; Zhou
and Chellappa, 2004). Theoretically, the light-field
model provides pose-invariant recognition of images
taken with arbitrary camera and pose when the illu-
mination condition is fixed. Zhou et al. extended the
light-field model to a bilinear model which allows si-
multaneous change of pose and illumination (Zhou
and Chellappa, 2004). However, in practice, the cam-
era pose of the test image has to be known beforehand
to compare it with the pre-computed light-field, which
effectively amounts to knowing the correspondence in
3D model-based approaches. This model is also un-
able to extend to the representation to a novel pose.
In the super-resolution field, the idea of using la-
tent subspaces in generative models has been sug-
gested by (Capel and Zisserman, 2001; Gunturk et al.,
2003). However the learned subspaces reflect mixed
contributions from pose, illumination, subject identi-
ties, etc. In our case the subspace encodes 3D struc-
ture, albedo and the low-pass filtering nature of the
Lambertian reflectance function (Basri and Jacobs,
2003), and the pose change is dedicated to geometric
transforms. Furthermore, we show how to learn the
basis, pose and illumination conditions directly and
simultaneously from a few images of both unknown
pose and illumination. In our method we estimate
the geometric warping variable via a continuous opti-
mization instead of searching over a limited or finite
set of predefined transformations (Hardie et al., 1997;
Frey and Jojic, 1999; Tipping and Bishop, 2002).
The remainder of the paper is organized as fol-
lows. In Sec. 2, we formulate the warped subspace
model in a probabilistic generative framework, and
describe how to jointly estimate the pose and the il-
lumination with a known basis. In Sec. 3, we de-
scribe a maximum a posteriori (MAP) approach to the
learning of a basis as well as the estimation of pose
and illumination simultaneously, and explain how a
prior distribution and efficient optimization can be
employed to learn the model. In Sec. 4, we perform
recognition experiments on real data sets. We con-
clude with discussions in Sec. 5.
2 JOINT ESTIMATION OF POSE
AND ILLUMINATION
In this section we explain the elements of genera-
tive models of images and optimization techniques to
jointly estimate pose and illumination.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
220

2.1 Generative Model of Multi-view
Images
A simple generative model common to super-
resolution methods is the following:
x = W
g
z +ε, (1)
where x is an observed image, z is a latent image,
and W
g
is a warping operator on the latent image:
let z(u,v) be the pixel intensity at (u,v) ∈ R
2
and
T
g
: R
2
→ R
2
be a transform of coordinates parama-
terized by g, then
(W
g
z)(u,v) = z(T
−1
g
(u,v)).
In the finite-pixel domain, we assume x and z are D-
dimensional vectors of image intensities where D is
the number of pixels, and W
g
is a D × D matrix rep-
resenting the warping and the subsequent interpola-
tion. From the definition above, the W
g
is a nonlin-
ear function of warping variables g; however, it is a
linear function of images z, which can be seen by
the equality W
g
(a
1
I
1
+ a
2
I
2
) = a
1
(W
g
I
1
) + a
2
(W
g
I
2
),
for any two images I
1
and I
2
and real numbers a
1
and
a
2
.
We consider the perspective transforms in this
paper, so g is a 8-dimensional vector. The X =
{x
1
,..., x
N
} and G = {g
1
,..., g
N
} denote aggregates of
N observed images and N warping variables.
If the noise ε is an independent, additive Gaus-
sian noise, that is p(x|z,g) ∼ N (W
g
z,Ψ), then the log-
likelihood of the observed samples X becomes
L = log p(X|z,G) =
∑
i
log p(x
i
|z,g
i
)
= −
1
2
∑
i
(x
i
−W
g
i
z)
0
Ψ
−1
(x
i
−W
g
i
z) (2)
plus a constant. The maximum likelihood (ML) esti-
mates of the latent image z and the warping parame-
ters G are found by computing
argmin
z,G
∑
i
(x
i
−W
g
i
z)
0
Ψ
−1
(x
i
−W
g
i
z).
2.2 Warped Illumination Subspace
The previous model (1) can only explain the change
of appearance from a single latent image. Instead, we
want z to be a combination of basis images z = Bs,
where B is a D × d matrix and s is d-dimensional
vector and d D. Our choice of B comes from
the low-dimensional nature of illumination subspaces
of convex Lambertian objects: an image illuminated
from arbitrary light source distribution can be ap-
proximated well by a combination of four or nine-
dimensional basis (Basri and Jacobs, 2003). In this
setting, B encodes 3D structure, albedo and the low-
pass filtering nature of Lambertian reflectance, and
the variables s determine the distribution of light
sources. Let us call s illumination coefficients.
The corresponding generative model is
x = W
g
Bs + ε. (3)
Since the warping W
g
is a linear transform of im-
ages, the W
g
maps a subspace to another subspace. In
this sense we call our model a warped subspace model
(refer to Fig. 2).
2.3 Optimization
Given an ensemble of images of the same object with
unknown illumination and pose, we can learn g
i
and
s
i
by minimizing the ML cost:
C = −2log p(X|B,S,G)
=
∑
i
kx
i
−W
g
i
Bs
i
k
2
Ψ
. (4)
We will use the notation kyk
2
Ψ
to denote the quadratic
form kyk
2
Ψ
= y
0
Ψ
−1
y. In super-resolution approaches,
the warping variables g
i
are typically computed once
in a preprocessing step. Since we are dealing with
images under arbitrary illumination change, a direct
registration based on intensity is bound to fail. We
overcome this problem by updating the registration
variable g and illumination coefficient s in an alter-
nating fashion.
2.3.1 Estimating Warping Variables g
To minimize (4) with respect to g we use a multi-
scale registration technique (Vasconcelos and Lipp-
man, 2005) to speed up computations and avoid local
minima. At each level of coarse-to-fine image res-
olutions, registration is done by the Gauss-Newton
method described in the following.
For simplicity assume the cost C is the sum of
squared differences of two images I
1
and I
2
C =
∑
u,v
[I
1
(u,v) − I
2
(T
−1
g
(u,v))]
2
. (5)
The Gauss-Newton method finds the minimum of (5)
by the update rule:
g
n+1
= g
n
− α(∇
2
g
C |
g
n
)
−1
∇
g
C |
g
n
, (6)
where ∇
g
C and ∇
2
g
C are the gradient and the Hessian
of C, respectively. These are computed from the first-
and the second-order derivatives of T with respect to
g, and the first- and the second-order derivatives of
images with respect to the coordinates (u,v).
To apply the technique, we first generate image
pyramids for I
1
and I
2
, we update g by (6) at the coars-
est level of the pyramids until convergence, and repeat
the iteration at the finer levels.
LEARNING A WARPED SUBSPACE MODEL OF FACES WITH IMAGES OF UNKNOWN POSE AND
ILLUMINATION
221

Basis (B) Illuminated (x=Bs)
Warped (x=WBs)Original
Figure 3: Modeling pose and lighting changes with a warped subspace model. By estimating the illumination coefficients
s and the warping variables g with a known basis B, we can imitate the original pose and lighting on the left by the linear
combination (x = Bs) followed by the geometrical warping (x = W
g
Bs).
2.3.2 Estimating Illumination Coefficients s
Minimizing the cost (4) with respect to s is straight-
forward. By setting
∂C
∂s
i
= 2B
0
W
0
i
Ψ
−1
(W
i
Bs
i
− x
i
) = 0
we get the linear equation
(B
0
W
0
i
Ψ
−1
W
i
B)s
i
= B
0
W
i
Ψ
−1
x
i
, (7)
which can be directly solved by inverting d × d ma-
trix. Note that d D.
2.4 Experiments with Synthetic Data
We test the alternating minimization scheme with
synthetic face data. For this purpose, we first gen-
erated synthetic images from a 3D model of a per-
son with a fixed pose and varying illuminations, from
which an empirical basis B is computed by singu-
lar value decomposition (SVD). The number of basis
vector d = 5 was chosen to contain more than 98.8
percent of the total energy, which agrees with empir-
ical (Epstein et al., 1995) and analytical (Ramamoor-
thi, 2002) studies.
A number of images were randomly rendered with
varying pose (|yaw| ≤ 15
◦
,|pitch| ≤ 12
◦
) and vary-
ing light source direction (|yaw| ≤ 60
◦
,|pitch| ≤ 50
◦
).
The noise statistics Ψ were manually determined
from the statistics of the error between the true and
the reconstructed images. Figure 3 shows the basis
images and the result of joint estimation.
3 SIMULTANEOUS LEARNING
OF BASIS
In the previous section we showed how to jointly esti-
mate pose and lighting conditions of test images from
a known basis. However, in practice we do not know
the basis for a given person beforehand. In this sec-
tion we demonstrate an efficient method of learning
the basis as well.
3.1 MAP Estimation
By considering B also as an unknown variable the ML
cost (4) becomes certainly harder to minimize. The
main difficulty lies in the degeneracy of the product
W Bs. First, the product Bs is degenerate up to ma-
trix multiplications of any nonsingular matrix A, that
is, Bs = BA
−1
As. We will impose orthogonality on
the basis B
0
B = I, but the B and s are still degener-
ate up to a d × d rotation matrix. Secondly, W and
Bs are also degenerate. One can warp the basis by
some transformation T and compensate it by its in-
verse: W Bs = W T
−1
T Bs.
To relieve the difficulty, we assume a Gaussian
process prior on B and a Gaussian density prior on
g. These priors can break the degeneracy by prefer-
ring specific values of (W,B, s) among those which
give the same value of W Bs.
3.1.1 Gaussian Process Prior for Images
In super-resolution problems, finding latent images
z is usually ill-posed and a prior is required for z.
One of the commonly used priors is the Gaussian
MRF (Capel and Zisserman, 2003) of the form p(z) =
1
Z
exp(−z
0
Qz), which can be viewed as a Gaussian
random process prior on z ∼ N (µ,Φ) whose covari-
ance reflects the MRF properties.
We propose the following prior: if b
j
denotes the
j-th column of B, then each {b
j
} has the i.i.d. Gaus-
sian prior b
j
∼ N (µ, Φ) . It is typical to assume µ
i
= 0
for allow arbitrary images, but we can also use the
empirical basis images, such as those from the pre-
vious experiments with synthetic faces. We further
assume b
j
’s are indepent. For Φ we choose RBF co-
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
222

variance described in (Tipping and Bishop, 2002): if
the i-th and j-th entries of z correspond to the pix-
els (u
i
,v
i
) and (u
j
,v
j
) in image coordinates, then
[Φ]
i j
∝ exp
−
1
2r
2
{(u
i
− u
j
)
2
+ (v
i
− v
j
)
2
}
. The in-
verse Q = Φ
−1
of the RBF covariance penalize abrupt
changes in the values of nearby pixels and act as a
smoothness prior. In practice, the Q = Φ
−1
need not
be invertible, and can be made sparse to speed up
computations. The independence assumption on the
basis images {b
j
} may seem too restrictive, because
the basis images {b
j
} may be correlated. However,
the MRF prior serves mainly as the smoothness reg-
ularizer and the independence only implies that the
basis images are independently smooth. Besides, as-
suming the full dependency of basis images is not
practical due to the sheer size of the covariance ma-
trix.
3.1.2 Regularized Warping
A prior for g can prevent unrealistic over-registration
and make the problem better-posed. We penalized the
L
2
norm of the displacement field. Suppose (δu,δv) =
T
g
(u,v) − (u,v) is the displacement field of the trans-
form T
g
, then the norm
∑
(u,v)
(δu)
2
+ (δv)
2
mea-
sure the overall distortion the transform T
g
induces.
The second-order approximation to the squared norm
around g = 0 is
∑
(u,v)
{(∇
g
δu)
0
g}
2
+ {(∇
g
δv)
0
g}
2
= g
0
Λg
The corresponding regularization term log p(g) =
−λg
0
Λg is added to the registration error term (5) in
our multiscale registration procedure. For perspective
transforms, the Λ is a 8 × 8 matrix which doesn’t de-
pend on data.
3.2 Optimization
The proposed MAP cost is as follows:
C = −2log [p(X|B,S,G)p(B)p(G)]
=
∑
i
kx
i
−W
g
i
Bs
i
k
2
Ψ
+ λ
∑
i
g
0
i
Λg
i
+ηN
∑
j
kb
j
− µ
j
k
2
Φ
+ const (8)
The minimization is similarly done by alternating be-
tween minimizations over B, s and g. Minimizing
over the latter two is the same as previous section,
and we only describe minimization over B.
3.2.1 Finding Basis Images B
The derivative of C w.r.t B is
∂C
∂B
= 2
∑
i
W
0
i
Ψ
−1
(W
i
Bs
i
− x
i
)s
0
i
+2ηNΦ
−1
(B − µ),
where µ = [µ
1
....µ
d
]. An exact solution is given by
setting
∂C
∂B
= 0:
∑
i
W
0
i
Ψ
−1
(W
i
Bs
i
− x
i
)s
0
i
+ ηNΦ
−1
(B − µ) = 0. (9)
We can solve the equation either directly or by a con-
jugate gradient method. After updating B, we orthog-
onalize it by a Gram-Schmidt procedure.
3.3 Algorithm
The final algorithm is summarized below:
1. initialize g, s and B.
2. for i = 1, ...,N, minimize C over g
i
by multi-
scale registration.
3. for i = 1,...,N, solve (7) for s
i
by inversion.
4. solve (9) for B by scaled conjugate gradient.
5. orthogonalize B by Gram-Schmidt procedure.
6. repeat 2–5 until convergence.
4 APPLICATIONS TO FACE
RECOGNITION
In this section we perform prediction and recognition
experiments with real images from the Yale face and
CMU-PIE databases.
4.1 Yale Face Database
The Yale face database (Georghiades et al., 2001)
consists of images from 10 subjects under 9 different
poses and 43 different lighting conditions.
1
From the
original images we roughly crop face regions and re-
size them to 40 × 40 images (D = 1600). Each image
is then normalized to have the same sum-of-squares.
All images are globally rescaled to have the min/max
value of 0/1.
As a training set of each subject we randomly se-
lect two images with arbitrary lighting condition per
pose, to get a total of 2 × 9 = 18 images of unknown
1
two of the lighting conditions (‘A-005E+10’ and
‘A+050E-40’) are dropped due to erroneous recording.
LEARNING A WARPED SUBSPACE MODEL OF FACES WITH IMAGES OF UNKNOWN POSE AND
ILLUMINATION
223

pose and illumination of the subject. The test set of
each subject comprises all remaining images which
are not in the training set (43 × 9 − 18 = 369) of the
subject. The 43 lighting conditions in the test set are
divided into four subsets as explained in (Georghiades
et al., 2001) according to the angle the light source
direction makes with the frontal direction. The four
subsets consists of 6, 12 , 12, and 13 lighting condi-
tions respectively with increasing angles.
We generated multiple pairs of training/test sets to
get averaged results from random choices of training
set.
4.2 CMU PIE Database
The CMU-PIE database (Sim et al., 2003) consists of
images from 68 subjects under 13 different poses and
43 different lighting conditions.
We arbitrarily chose the same number (=10) of
subjects as the Yale face in our tests.Among 13 origi-
nal camera poses, we have chosen 7 poses whose an-
gles with the frontal camera pose are roughly less than
40
◦
,
2
and 21 lighting conditions without background
lights. We similarly detect and crop face regions from
the original data to a size of 40 × 40 and rescale the
intensity.
As a training set of each subject we randomly se-
lect two images of arbitrary lighting condition per
pose to get a total of 2 × 7 = 14 images of unknown
pose and illumination of the subject. The test set of
each subject comprises all remaining images which
are not in the training set (21 × 7 − 14 = 133) of the
subject. We also divided the testing set into three sub-
sets, according to the angle the light source direction
makes with the frontal axis (0 − 20
◦
,20 − 35
◦
,35 −
67
◦
). The four subsets consists of 7, 6, and 8 lighting
conditions respectively.
We also generated multiple pairs of training/test
sets for CMU PIE.
4.3 Parameter Selection
In an earlier section we empirically determined the
value of d and Ψ from synthetic data. Similarly, we
manually chose the parameters {λ,η,Φ} by experi-
menting with synthetic faces. The λ relates to the
amount of warping and {η, Φ} relates to the smooth-
ness of images. As these parameters do not reflect the
peculiarity of each person, we can the same values for
the Yale face and CMU PIE database as the values for
synthetic data without exhaustive fine-tunings.
2
cameras numbered ‘05’, ‘07’, ‘09’, ‘11’, ‘27’, ‘29’,
‘37’
Table 1: Average prediction error kx − ˆxk
2
/kxk
2
of linear
vs warped subspace models from the Yale face (upper) and
and CMU PIE (lower) databases.
Subset # 1 2 3 4
Linear 0.0568 0.0676 0.1056 0.1837
Warped 0.0124 0.0154 0.0269 0.0609
Subset # 1 2 3
Linear 0.0887 0.1068 0.1535
Warped 0.0149 0.0174 0.0359
4.4 Prediction Results
We demonstrate the advantage of having a nonlin-
ear warping to a linear subspace model in prediction.
From 18 (and 14) images of a person from the Yale
face (and CMU PIE) database, we learn the two sets
of bases:
• Linear subspace: 5-dimensional basis B
j
lin
is
computed from SVD of the training data of
j-th subject. The prediction ˆx is given by
ˆx = B
j
lin
(B
j
lin
)
0
x.
• Warped subspace: 5-dimensional basis B
j
warp
,
warping variable g
j
, and light coefficients s
j
are
computed from the training data of j-th subject,
by minimizing the MAP cost (8) iteratively from
the initial value B
j
lin
. The prediction ˆx is given by
ˆx = W
g
j
B
j
warp
s
j
.
Figure 4 shows sample results from the two meth-
ods.
Quantitative evaluations are performed as follows.
Prediction error for each image is defined as the frac-
tional error between true the image x and the predicted
image ˆx: err = kx − ˆxk
2
/kxk
2
averaged over all test
images. The result is shown in Table 1. Our method
reduces the error to 16 ∼ 33 percent of the error from
the linear model.
4.5 Recognition Results
We compare recognition performance of our method
with four other standard appearance-based methods
suggested in (Georghiades et al., 2001). These in-
clude the nearest-neighbor classifiers which do not
use subject identity in training: correlation, eigenface,
and eigenface without the first three eigenvectors. For
these we have used 50 eigenvectors. The other two
methods are the same as in the prediction experiments
(linear subspace and warped subspace). The aver-
age recognition errors were computed over all con-
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
224

Linear subspace Warped subspace
Original
Learned basis :
Linear subspace Warped subspace
Original
Learned basis :
Figure 4: Experiments with the Yale face (upper) and CMU PIE (lower) databases. Reconstructions of the original images
with a linear subspace model (middle) and with a warped subspace model (right) are compared along with the learned bases
from the two methods. The warped subspace model shows increased resolutions and sharpness in the learned basis and the
reconstructed images.
ditions and all subjects from Yale face and CMU PIE
databases, shown in Fig. 5.
5 CONCLUSIONS
The Eigenface is an almost two-decade old subspace
model. Still, it serves as a fundamental image-based
model due to its simplicity. In this work we re-
vamped the subspace model to a warped subspace
model which can cope with both the linear variability
in illumination and the nonlinear variability in pose.
Given a few training images, the model can estimate
the basis, pose and illumination conditions simulta-
neously via MAP estimation and multiscale registra-
tion technique. Experimental results confirm the ad-
vantage of the warped subspace model over the stan-
dard image-based models in prediction and recogni-
tion tasks. We are currently working on increasing
the range of pose our model can handle.
REFERENCES
Basri, R. and Jacobs, D. W. (2003). Lambertian reflectance
and linear subspaces. IEEE Trans. Pattern Analysis
and Machine Intelligence, 25(2):218–233.
Capel, D. and Zisserman, A. (2003). Computer vision ap-
plied to super resolution. IEEE Signal Processing
Magazine, 20(3):75–86.
Capel, D. P. and Zisserman, A. (2001). Super-resolution
from multiple views using learnt image models. In
CVPR, volume 2, pages 627–634.
Epstein, R., Hallinan, P., and Yuille, A. (1995). 5 ± 2
Eigenimages suffice: An empirical investigation of
low-dimensional lighting models. In Proceedings of
IEEE Workshop on Physics-Based Modeling in Com-
puter Vision, pages 108–116.
Frey, B. J. and Jojic, N. (1999). Transformed component
analysis: Joint estimation of spatial transformations
and image components. In ICCV, page 1190, Wash-
ington, DC, USA. IEEE Computer Society.
Georghiades, A. S., Belhumeur, P. N., and Kriegman, D. J.
(2001). From few to many: Illumination cone mod-
els for face recognition under variable lighting and
LEARNING A WARPED SUBSPACE MODEL OF FACES WITH IMAGES OF UNKNOWN POSE AND
ILLUMINATION
225
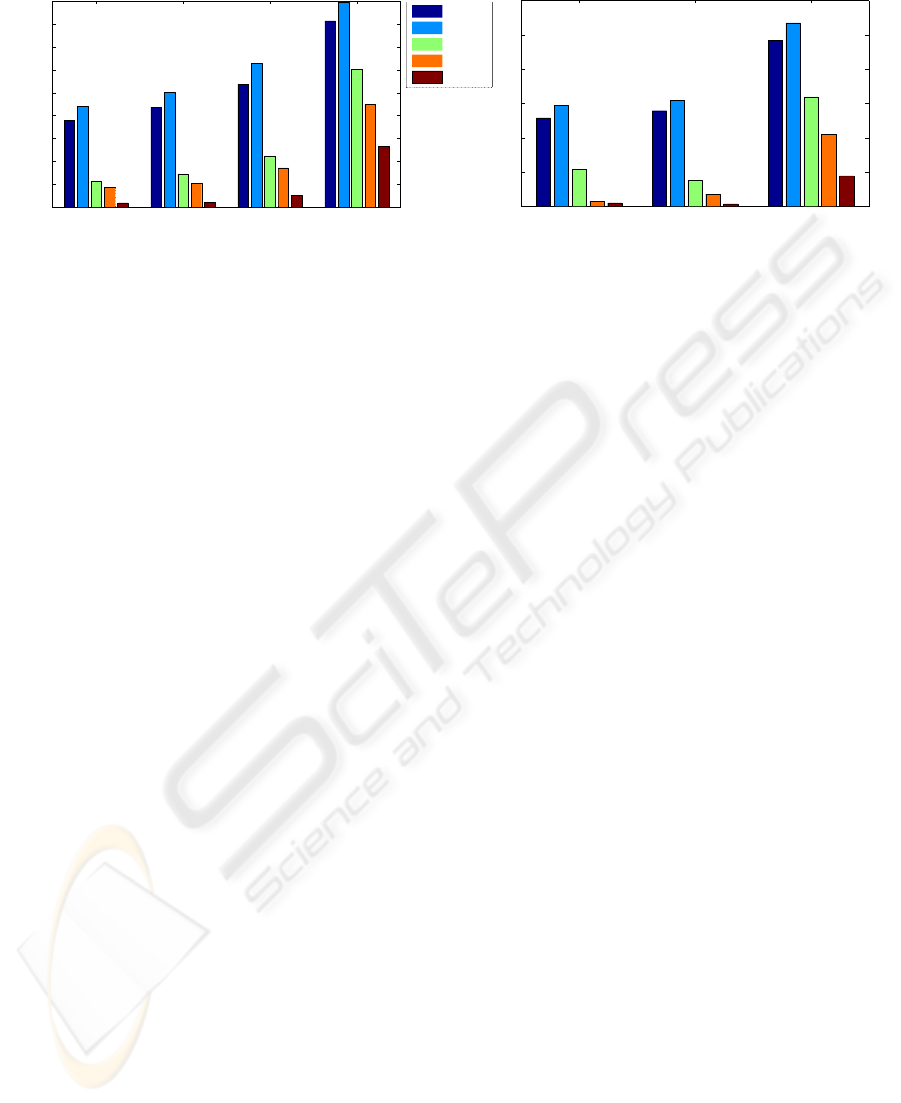
1 2
3
4
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
corr
eig
eigwo3
linear
warped
1 2 3
0
0.05
0.1
0.15
0.2
0.25
Yale face CMU PIE
Error rate
Subset #
Subset #
Figure 5: Average recognition error of five algorithms for the Yale face (left) and CMU PIE (right) databases. The warped
subspace model achieves the smallest error across different test subsets of lighting variations.
pose. IEEE Trans. Pattern Analysis and Machine In-
telligence, 23(6):643–660.
Gross, R., Matthews, I., and Baker, S. (2002a). Eigen
light-fields and face recognition across pose. In FGR
’02: Proceedings of the Fifth IEEE International Con-
ference on Automatic Face and Gesture Recognition,
page 3, Washington, DC, USA. IEEE Computer Soci-
ety.
Gross, R., Matthews, I., and Baker, S. (2002b). Fisher light-
fields for face recognition across pose and illumina-
tion. In Proceedings of the 24th DAGM Symposium
on Pattern Recognition, pages 481–489, London, UK.
Springer-Verlag.
Gunturk, B. K., Batur, A. U., Altunbasak, Y., III, M. H. H.,
and Mersereau, R. M. (2003). Eigenface-domain
super-resolution for face recognition. IEEE Trans. Im-
age Processing, 12(5):597–606.
Hallinan, P. (1994). A low-dimensional representation of
human faces for arbitrary lighting conditions. In Proc.
IEEE Conf. Computer Vision and Pattern Recognition,
pages 995–999.
Hardie, R. C., Barnard, K. J., and Armstrong, E. E. (1997).
Joint MAP registration and high-resolution image es-
timation using a sequence of undersampled images.
IEEE Trans. Image Processing, 6(12):1621–1633.
Ramamoorthi, R. (2002). Analytic PCA construction for
theoretical analysis of lighting variability in images of
a Lambertian object. IEEE Trans. Pattern Analysis
and Machine Intelligence, 24(10):1322–1333.
Sim, T., Baker, S., and Bsat, M. (2003). The CMU pose,
illumination, and expression (PIE) database. IEEE
Trans. Pattern Analysis and Machine Intelligence,
25(12):1615 – 1618.
Tipping, M. E. and Bishop, C. M. (2002). Bayesian im-
age super-resolution. In Becker, S., Thrun, S., and
Obermayer, K., editors, NIPS, pages 1279–1286. MIT
Press.
Turk, M. and Pentland, A. P. (1991). Eigenfaces for recog-
nition. Journal of Cognitive Neuroscience, 3(1):71–
86.
Vasconcelos, N. and Lippman, A. (2005). A multiresolution
manifold distance for invariant image similarity. IEEE
Trans. Multimedia, 7(1):127–142.
Zhou, S. K. and Chellappa, R. (2004). Illuminating light
field: Image-based face recognition across illumina-
tions and poses. In FGR, pages 229–234. IEEE Com-
puter Society.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
226
