CONTENT-BASED SHAPE RETRIEVAL USING DIFFERENT

AFFINE SHAPE DESCRIPTORS

Fatma Chaker, Faouzi Ghorbel

Ecole Nationale des Sciences de l’Informatique, Campus Universitaire La Manouba, Tunis, Tunisie

Mohamed Tarak Bannour

Ecole Nationale des Sciences de l’Informatique, Campus Universitaire La Manouba, Tunis, Tunisie

Keywords: Affine invariance, CBIR, Fourier Descriptors, Curvature Scale Space Descriptors, Retrieval, Shape.

Abstract: Shape representation is a fundamental issue in the newly emerging multimedia applications. In the Content

Based Image Retrieval (CBIR), shape is an important low level image feature. Many shape representations

have been proposed. However, for CBIR, a shape representation should satisfy several properties such as

affine invariance, robustness, compactness, low computation complexity and perceptual similarity

measurement. Against these properties, in this paper we attempt to study and compare three shape

descriptors: two issued from Fourier method and the Affine Curvature Scale Space Descriptor (ACSSD).

We build a retrieval framework to compare shape retrieval performance in terms of robustness and retrieval

performance. The retrieval performance of the different descriptors is compared using two standard shape

databases. Retrieval results are given to show the comparison.

1 INTRODUCTION

In the newly emerging multimedia applications such

as MPEG-4 and MPEG-7, shape plays an important

role in supporting the so called content based

functionalities. Many shape representations have

been proposed for various purposes. These methods

can generally be grouped into contour-based and

region-based.

For CBIR purpose, a shape representation

should be affine invariant, robust, compact, easy to

derive and perceptually meaningful. In terms of

these properties, Fourier Descriptors (FD) and

Curvature Scale Space Descriptors (CSSD) have

been recognized as suitable for CBIR. CSSD has

been adopted in MPEG-7 as shape descriptors.

In a previous work (Chaker and al., 2003a,b)

we have proposed a new complete and stable set of

Affine Invariant Fourier Descriptors (AIFD).

Experiments have shown that these descriptors have

good retrieval accuracy and if applied to the shape of

a curve it can deal with affine transformed curves

(Chaker and al., 2007). In this paper, we will test the

performance of AIFD in the context of shape

retrieval and we will compare it to two well known

affine descriptors such as the Affine Fourier

Descriptors (AFD) proposed by Arbter (Arbter,

1990) and the Affine Curvature Scale Space

Descriptor (ACSSD) (Mokhtarian and al., 2002). We

will show that the AIFD outperforms the AFD and

the ACSSD in terms of retrieval accuracy and

efficiency and are very robust against affine

transformations and much more for strong

distortions such perspective distortions.

The rest of the paper is organized as follows:

In Section 2, we remind in detail the

formulation of each descriptor. Section 3 gives the

experimental results and discussion follows. Section

4 concludes the paper.

2 AFFINE INVARIANT SHAPE

DESCRIPTORS

A number of shape representations have been

proposed to recognise shapes under affine

transformation (Arbter, 1990; Chaker and al.

2003a,b) (Mokhtarian and al., 2002). In these

497

Chaker F., Ghorbel F. and Tarak Bannour M. (2008).

CONTENT-BASED SHAPE RETRIEVAL USING DIFFERENT AFFINE SHAPE DESCRIPTORS.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 497-500

DOI: 10.5220/0001074704970500

 SciTePress

methods, the basic idea is to use a parameterisation

which is robust with respect to affine transformation,

i.e. affine length (Arbter, 1990). The shortcomings

of the affine length include the need for higher order

derivatives which results in inaccuracy, and

inefficiency as a result of computation complexity.

We propose here to use B-spline. Indeed, it’s well

known that these functions have good smoothing

quality and are robust relatively to multiple

derivatives and rounding errors.

In the rest of the paper we assume that all of the

contours are re-parameterized by affine arclength.

For a parametric contour

, given by its

Cartesian coordinates x and y (formally,

))(,)(()( tytxt =

where

represent the associated

parameter). We re-parameterized the contour using

the affine-length parameter:

∫

∧=

dttt

3/2

)(")('

)(

γγ

(1)

where L denotes the total equi-affine length of the

considered contour.

2.1 Affine Invariant Fourier

Descriptors (AIFD)

Let

and

be positive real numbers,

and

four positives integers. Let

and

be the

complex Fourier coefficients of the coordinates

and

, Δ denotes the determinant and

⎟

⎠

⎞

⎜

⎝

⎛

Δ=Δ

The both families of descriptors

and

are

respectively given by Eq.2 and Eq.3. For more

details, derivations, proofs, the reader is referred to

(Ghorbel, 1998).

() ()()

⎪

⎩

⎪

⎨

⎧

ΔΔ

ΔΔΔ=

Δ=

+−+−

−−−

βα

)(

(2)

for all

{}

210

,, kkkINk −∈

() ()()

⎪

⎩

⎪

⎨

⎧

ΔΔ

ΔΔΔ=

Δ=

+−+−

−−−

βα

)(

(3)

for all

{

}

321

,, kkkINk −∈

2.2 The Affine Fourier Descriptors

(AFD)

Let X

, Y

the Fourier coefficients of x(t), y(t)

respectively, the following normalized coefficients

are affine-invariants when the parameter t is linear

under affine transformation.

[

]

[]

,det

pppp

YYYX

−

(4)

,...2,1,0 ±±=≠Δ k

p is a constant and p

≠

0. In his experiments, Arbter

(Arbter, 1990) utilize the area parameterization

instead of the affine arclength. The Euclidean

distance between two feature vectors was used as the

similarity measurement.

2.3 Affine Curvature Scale Space

Descriptor (ACSSD)

Consider a parametric vector equation for a

curve

))(,)(()( sysxs

. The formula for computing

the curvature function can be expressed as:

()

2/3

)()(

)()()()(

)(

sysx

sysxsysx

&&&&&&

−

(5)

where

and

&&&&

are the first and second

derivatives at location s respectively (s is the affine

normalised arc length). If

),(

sg , a 1-D Gaussian

kernel of width σ, is convolved with each

component of the curve, then X (s, σ) and Y (s, σ)

represent the components of the resulting curve,

),()(),(

σσ

sgsysY

sgsxsX

∗=

∗

(6)

the curvature of

is given by:

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

498

() ()

()

2/3

),(),(),(),(

),(

σσ

σκ

sYsX

sYsYsYsX

ssssss

−

(7)

The CSS descriptor extraction algorithm is

described in (Abassi and al., 2000; Mokhtarian and

al., 2002). The CSS descriptor vector represents a

multiscale organization of the curvature zero-

crossing points of a planar curve. In this sense, the

descriptor dimension varies for different shapes, thus

a special matching algorithm is necessary to

compare two CSS descriptors. We implemented the

Matlab prototype presented in (Ming, 1999).

3 A COMPARATIVE STUDY FOR

SHAPE-BASED RETRIEVAL

3.1 Test Setup

- Multiview Curve Dataset (MCD) (Zuliani,

2004): This dataset comprises 40 shape

categories, each corresponding to a shape

drawn from an MPEG-7 shape category. Each

category in the new dataset contains 7 curve

samples that correspond to different

perspective distortions of the original shape.

The original MPEG-7 shapes were printed on

white paper and 7 samples were taken using a

digital camera from various angles (Figure 1).

The contours were extracted from the iso-

intensity level set decomposition of the images

(Lisani, 2001).

(a) (b) (c)

(d) (e) (f)

(g)

Figure 1: Some Examples of Images from the MCD

database acquired from different viewpoints; (a) : Central

(b) Bottom (c) Left (d) Right, (e) Top (f) Top-left, (g)

Bottom- Right.

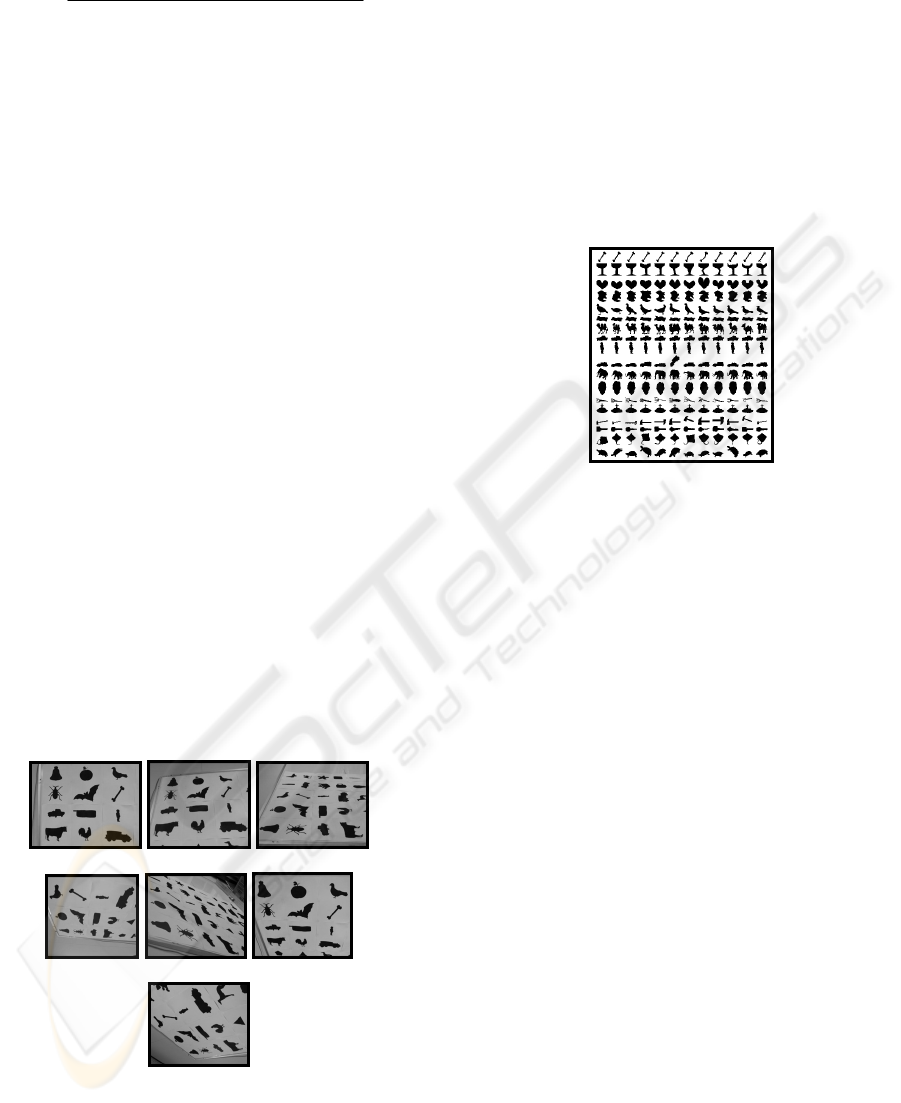
- MPEG-7 contour shape database CE-1 Part B:

this set takes into consideration of common

shape distortions in nature and the inaccuracy

nature of shape boundaries from segmented

shapes. Set B is for testing of similarity-based

retrieval or for testing shape descriptors’

robustness to various arbitrary shape

distortions. In our experiments we have used a

sample from the MPEG-7 database (216

shapes) (Figure 2). This dataset contains

eighteen categories with twelve shapes in each

category.

Figure 2: The 216 shapes from MPEG-7 contour shape

database CE-1 Part B.

3.2 Retrieval Results

The performance of the retrieval is evaluated using

precision and recall pair (PRP) which give the

percentage of retrieved information that is relevant

as a function of the percentage of relevant

information retrieved (Bimbo, 1999). For each

query, the precision of the retrieval at each level of

the recall is obtained. The result precision of

retrieval is the average precision of all the query

retrievals. The average precision-recall of retrieval

using the three shape descriptors on each dataset are

shown in Fig. 3(a)-(b). Some screen shots of

retrieval are shown in Fig. 4 and Fig. 5. In all the

screen shots, the top left shape is the query shape.

The retrieved shapes are ranked in descending order

of similarity to the query shape.

It is clear from the precision-recall charts that the

retrieval performance using AIFD is the best among

the three. Although the affine FD is designed to

particularly target affined shape description it is

expected to work fine for polygonal shape under

affine transformation. CSSD robustness to boundary

variations is very limited. It is not robust to common

boundary variations such as defections and arbitrary

distortions. On average, FD is better than CSSD,

while FD is much easier to derive, match, normalize

and more compact compared with affine CSSD.

CONTENT-BASED SHAPE RETRIEVAL USING DIFFERENT AFFINE SHAPE DESCRIPTORS

499

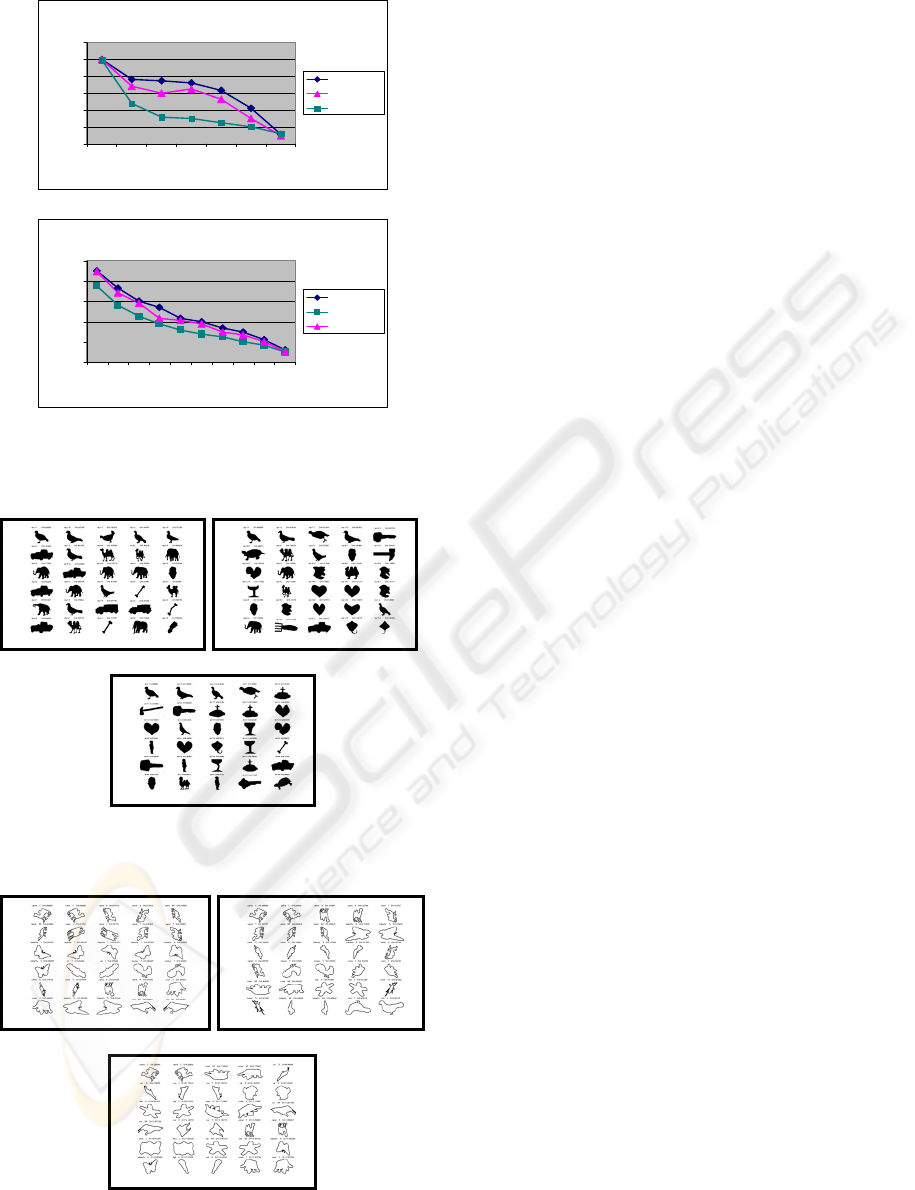
Precision/Recall Curve

100

120

14 26 53 72 76 86 97

Recall (%)

Precision (%)

AIFD

AFD

Affine CSSD

(a)

Precision/Recall Curve

100

10 20 30 40 50 60 70 80 90 100

Recall

Precision

AIFD

Affine CSSD

AFD

(b)

Figure 3: Retrieval effectiveness of AIFD, AFD and

Affine CSSD on (a) Multiview Curve Database. And (b)

MPEG-7 contour shape database.

(a) (b)

(c)

Figure 4: Retrieval of bird shapes from MPEG-7 Database

using (a) AIFD; (b) AFD; (c) Affine CSSD.

(a) (b)

(c)

4 CONCLUSIONS

In this paper we have made a comparative study on

three affine shape descriptors used for shape

retrieval. Results show that in terms of robustness

and retrieval accuracy the AIFD outperforms the

AFD and the affine CSSD. Although ACSSD

capture strong perceptual shape features, many

negative factors have affected its performance.

Indeed, the retrieval effectiveness of ACSSD is

severely affected by the complex matching method

which is an intrinsic problem of CSS description.

REFERENCES

Arbter, K., Snyder, W.E., Hirzinger, G. and Burkhardt, H.

“Application of affine-invariant fourier descriptors to

recognition of 3-d objects”, IEEE trans. Pattern

Analysis and Machine Intelligence, vol. 12, no. 7, pp.

640-646, 1990.

Abbasi, S., Mokhtarian, F. and Kittler, J. Enhancing CSS

based shape Retrieval for Objects with Shallow

concavities. Image and Vision Computing, 18:199–

211, 2000.

Bimbo, A. D. Visual Information Retrieval. pp. 56-57,

Morgan Kaufmann Publishers, Inc. San Francisco,

USA, 1999.

Chaker, F., Ghorbel, F. and Bannour, M.T. A complete

and stable set of affine invariant Fourier descriptors,

ICIAP’03, Mantova, Italy, September 2003.

Chaker, F. and Ghorbel, F. Stereo matching by affine

Invariant Fourier descriptors, ICIP’03, Barcelone,

Spain, September 2003.

Chaker, F., Ghorbel, F. and Bannour, M.T. Contour

retrieval and matching by Affine Invariant Fourier

Descriptors. IAPR Conference on Machine Vision

Applications (MVA07), pp. 291-294. May 16-18,

2007, Tokoyo, Japan.

Ghorbel, F.. Towards a unitary formulation for invariant

images description : application to images coding,

Annales des Télécommunications ; France 1998.

Lisani, J. L. shape Based Automatic Images Comparison,

PhD thesis, Université Paris IX- Dauphine, 2001.

Mokhtarian, F. and Abbasi, S. Shape Similarity Retrieval

under a Affine Transforms. Pattern Recognition,

35(31-41), 2002.

Ming, C. Y. Shape-Based Image Retrieval in Iconic Image

Databases. Master’s thesis, Chinese University of

Hong Kong, June 1999.

Zuliani, M. Bhagavathy, S., Manjunath, B. S. and Kenney,

C. S. Affine-Invariant Curve matching. 2004.

Figure 5: Retrieval of camel shapes from MCD Database

using (a) AIFD; (b) AFD; (c) Affine CSSD.

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

500