ROBUST ESTIMATION OF THE PAN-ZOOM PARAMETERS FROM
A BACKGROUND AREA IN CASE OF A CRISS-CROSSING
FOREGROUND OBJECT
J. Bruijns
Philips Research, High Tech Campus 36, 5656 AE, Eindhoven, The Netherlands
Keywords:
3DTV, 3D display, 3D processing, 2D-to-3D conversion, background motion estimation, foreground-
background segmentation.
Abstract:
In the field of video processing, a model of the background motion has application in deriving depth from
motion. The pan-zoom parameters of our background model are estimated from the motion vectors of parts
which are a priori likely to belong to the background, such as the top and side borders (”the background area”).
This fails when a foreground object obscures the greater part of this background area. We have developed a
method to extract a set of pan-zoom parameters for each different part of the background area. Using the
pan-zoom parameters of the previous frame, we compute from these sets the pan-zoom parameters most likely
to correspond to the proper background parts. This background area partition method gives more accurate pan
parameters for shots with the greater part of the background area obscured by one or more foreground objects
than application of the entire background area.
1 INTRODUCTION
For the introduction of 3DTV on the market (Fehn
et al., 2002; de Beeck et al., 2002), availability of 2D-
to-3D conversion is an important ingredient. As only
a very limited amount of 3D recorded content (stereo-
scopic or other) is available, 3DTV is only attractive
for a wide audience if existing material can be shown
in 3D as well. Within Philips Research, the technol-
ogy for fully automatic, real-time 2D-to-3D conver-
sion at the consumer side has been developed over the
past years (Barenbrug, 2006; Redert et al., 2007).
The 3D format used consists of the original 2D
video, augmented with a depth channel (the term
depth as used in this paper is strictly speaking a recip-
rocal depth or disparity). This depth channel allows
to render views from positions slightly displaced from
the original view point. These additional views can
then be interleaved and sent to a multi-view screen
such as the Philips 3DLCD. (Fehn, 2004; Berretty
et al., 2006).
The depth maps are generated using several depth
cues. One of the depth cues used is ”depth from mo-
tion” (Ernst et al., 2002). The depth-from-motion
method is for a static scene equivalent to the structure-
from-motion (SFM) methods. The camera calibration
part of the SFM methods is replaced by estimation of
a background motion: A motion model for objects at
large distance from the camera. All objects with (pos-
sibly independent)motions that do not conform to this
background model are supposed to be in front of the
background.
The background model is a pan-zoom model
(de Haan and Biezen, 1998):
m
x
= p
x
+ s
x
∗ ˆx
m
y
= p
y
+ s
y
∗ ˆy
(1)
with m = (m
x
,m
y
)
T
the background motion,
{ ˆx, ˆy} the pixel coordinates with regard to the opti-
cal center, {p
x
, p
y
} the pan parameters and{s
x
,s
y
} the
zoom parameters. Note that although theoretically,
s
x
≡ s
y
, we allow here two different values for the mo-
ment. This has as big advantage that the expressions
for the x and y motions decouple: there is no interac-
tion between them. We come back to this issue at the
end of Section 3.
The pan-zoom parameters should be estimated
from the motion vectors of the background blocks.
The motion vectors (see Figure 1 and 2; the blue
crosses are explained later on) are estimated using
8x8 pixel blocks (de Haan and Biezen, 1994). But
327
Bruijns J. (2008).
ROBUST ESTIMATION OF THE PAN-ZOOM PARAMETERS FROM A BACKGROUND AREA IN CASE OF A CRISS-CROSSING FOREGROUND
OBJECT.
In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 327-334
DOI: 10.5220/0001072103270334
Copyright
c
 SciTePress

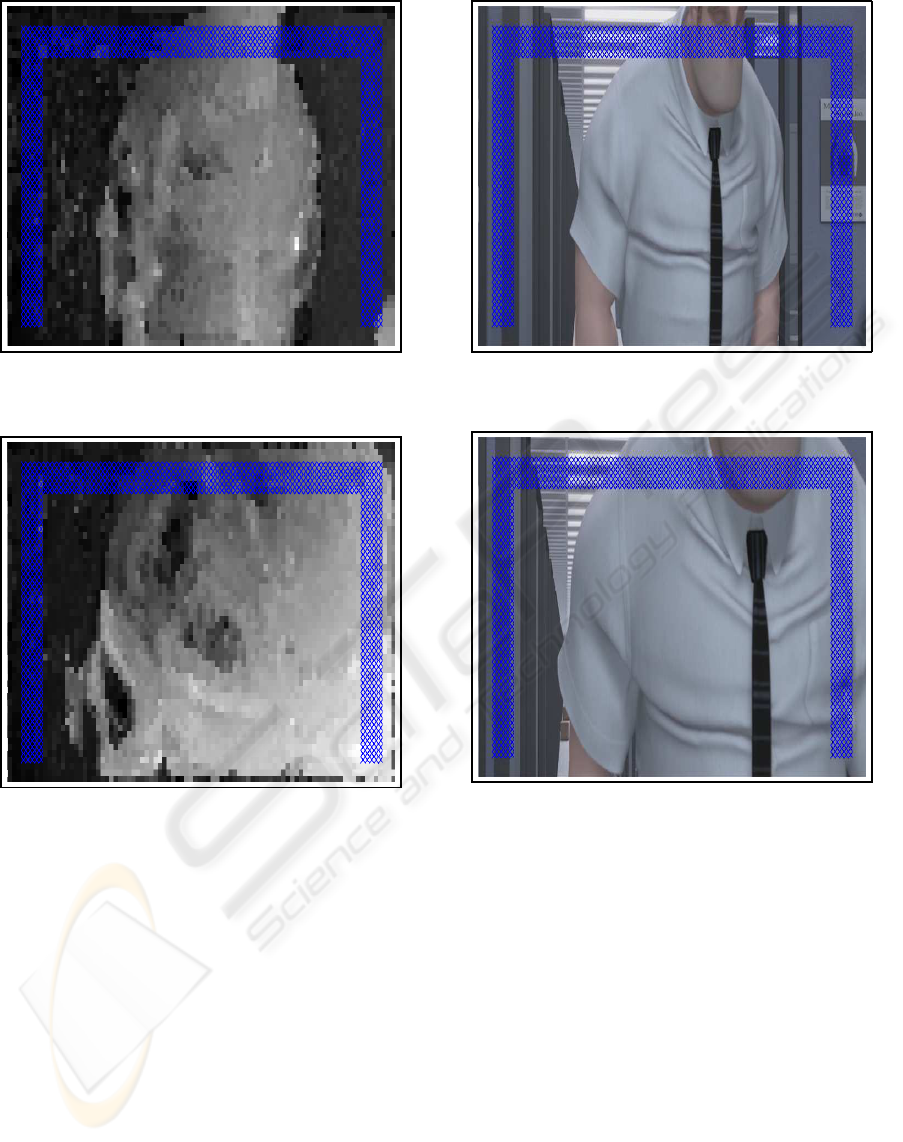
Figure 1: k Motion k field of video shot OFFICE for a
proper background area.
Figure 2: k Motion k field of video shot OFFICE for an
obscured background area.
because it is not known which blocks belong to the
background, blocks which are a priori likely to be-
long to the background are selected for estimation of
the pan-zoom parameters. The selected background
blocks (”the background area”) are blocks close to
the top of the image and blocks close to the left and
right image borders. Examples of background areas
are the set of blue crosses in Figure 3 and 4.
However, if a relatively large foreground object is
criss-crossing, the greater part of the background area
may be obscured (see Figure 4 and 2), resulting in er-
roneous pan-zoom parameters. We have developed a
method to extract a set of pan-zoom parameters for
each different part of the background area (i.e. the
proper background part and the obscured background
parts). We use the pan-zoom parameters of the previ-
Figure 3: Frame of video shot OFFICE with a proper back-
ground area.
Figure 4: Frame of video shot OFFICE with an obscured
background area.
ous frame to compute from these sets the pan-zoom
parameters most likely to correspond to the proper
background part.
Our method for robust estimation of the pan-zoom
parameters in case of a proper background area (i.e.
the majority of the blocks of the background area
are proper background blocks) using the entire back-
ground area (the ”EBA method”) is described in Sec-
tion 3. Our background area partition method (the
”BAP method”) for computation of the pan-zoom pa-
rameters in case of an obscured background area (i.e.
the majority of the blocks of the background area are
obscured by one or more foreground objects) is de-
scribed in Section 4. In Section 5 we present our re-
sults and in Section 6 we give some conclusions to
consider.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
328

2 RELATED WORK
The structure-from-motion (SFM) methods are the
only commonly known and successful methods for
2D-to-3D conversion. When a camera moves around
a static scene, SFM can provide very good conversion
results (Huang and Netravali, 1994; Azarbayejani and
Pentland, 1995; Zhang et al., 1995; Armstrong et al.,
1996; Beardsley et al., 1996; Xu and Zhang, 1996;
Falkenhagen, 1997; Pollefeys et al., 2000; Hartley
and Zisserman, 2001; Ernst et al., 2002). However,
several issues hamper wide use of SFM. First, if cam-
era parameters such as pixel aspect ratio and zoom
are unknown, they have to be estimated along with
the conversion. In this case many successive frames
with different viewpoints are required to define a sin-
gle solution (Armstrong, 1996; Pollefeys et al., 1998;
Pollefeys, 1999). Secondly, if camera movements are
very small or even absent, the mathematics become
singular and no solution can be obtained. Finally,
most scenes are not static, but contain independently
moving objects. Several methods exist to handle this,
e.g. (Xu and Zhang, 1996), but these methods again
require that camera or object motion is considerable
and that each individual object is rigid. Among the
most important video objects are humans, which are
far from rigid. So, in most cases accurate SFM is not
possible.
3 THE EBA METHOD
If only a very small portion of the blocks of the back-
ground area are obscured by foreground objects (see
Figure 3 and 1), the pan-zoom parameters can be es-
timated accurately provided that the outliers are re-
moved. Using Equation 1 local pan-zoom parame-
ters can be extracted from two or more blocks of the
background area. A set of local pan-zoom parameters
can be collected by selecting different subsets of the
background area. After the outliers are removed, the
global pan-zoom parameters can be computed by tak-
ing e.g. the average or the median of the remaining
set of local pan-zoom parameters.
To avoid the time-consuming computation for all
possible subsets of the background area (Ω(n
2
)), we
have implemented a two-stage method using single
blocks (O(n)). First, the zoom parameter is com-
puted. Secondly, using this zoom parameter the pan
parameters are computed. This method is based on
the relation between the zoom parameter and the par-
tial derivatives of the motion field:
∂m
x
∂x
=
∂(p
x
+ s
x
∗ ˆx)
∂x
= s
x
∂m
y
∂y
=
∂(p
y
+ s
y
∗ ˆy)
∂y
= s
y
(2)
Because there is only one zoom parameter (i.e.
s
x
≡ s
y
), we select only those blocks of the back-
ground area for which the two local zoom parameters
s
l,x
and s
l,y
(i.e. the two local partial derivatives ob-
tained from smoothed differences) are almost equal:
|s
l,x
− s
l,y
| ≤ t (3)
with the threshold t equal to the 25% percentile of
the absolute differences of the local zoom parameters
of the background area {|s
l,x
− s
l,y
|}.
The precise value of the threshold t is not so im-
portant as long as the blocks with a relatively large
difference between the two local zoom parameters
(i.e. the blocks with probably outliers) are removed.
After that we compute the global zoom parameter
s
g,x
(i.e. the s
x
of Equation 1) from the local zoom
parameters {s
l,x
} of the selected blocks using robust
statistical procedures (Marazzi, 1987) as follows:
1. Compute the robust standard deviation s
1
:
m
0
= median({s
l,x
})
m
1
= median(|{s
l,x
} − m
0
|)
s
1
= m
1
/Φ
−1
(0.75)
(4)
where Φ
−1
(0.75) is the value of the inverse stan-
dard Normal distribution at the point 0.75. As
Marazzi explains, the factor Φ
−1
(0.75) trans-
forms the absolute deviation m
1
to the standard
deviation s
1
.
2. Remove the outliers from {s
l,x
}.
We classify a local zoom parameter s
l,x
as an out-
lier if
|s
l,x
− m
0
| > s
1
∗ Φ
−1
(0.99) (5)
Assuming a Gaussian distribution, this means that
the probability that an inlier is classified as an out-
lier is less than 1.0%.
3. Compute the global zoom parameter s
g,x
from the
remaining local zoom parameters {s
l,x
}:
s
g,x
= median({s
l,x
}) (6)
After that the global zoom parameter s
g,y
(i.e. the
s
y
of Equation 1) is computed in the same way from
ROBUST ESTIMATION OF THE PAN-ZOOM PARAMETERS FROM A BACKGROUND AREA IN CASE OF A
CRISS-CROSSING FOREGROUND OBJECT
329

the selected local zoom parameters {s
l,y
}, we com-
pute the global zoom parameter s
g
from the two global
zoom parameters s
g,x
and s
g,y
:
s
g
= median(0,s
g,x
,s
g,y
). (7)
Application of this formula for the global zoom
parameter s
g
is based on the following reasoning:
1. In case s
g,x
= s
g,y
, the global zoom parameter s
g
should be equal to this value (i.e. s
g
= s
g,x
= s
g,y
).
2. Noise in the zoom estimate should be diminished.
In case both zoom estimates have the same sign,
the one closest to zero is taken; in case the zoom
estimates have a different sign, the global zoom
parameter is zero.
After the global zoom parameter s
g
is estimated,
the pan parameters p
x
and p
y
can be computed as fol-
lows:
1. Compute the local pan parameters {p
l,x
} and
{p
l,y
} for the selected blocks using Equation 1:
p
l,x
= m
x
− s
g
∗ ˆx
p
l,y
= m
y
− s
g
∗ ˆy
(8)
2. Compute the global pan parameters p
g,x
and p
g,y
from the local pan parameters {p
l,x
} respectively
{p
l,y
} using the same robust statistical procedure
as used for the computation of the global zoom
parameter s
g,x
.
4 THE BAP METHOD
If the majority of the blocks of the background area
are obscured by foreground objects (see Figure 4 and
2), the EBA method (see Section 3) gives wrong re-
sults for the pan parameters p
x
and p
y
(the possible
effect on and a possibly better procedure for the zoom
parameters will be discussed in Section 5 and Section
6). The large peaks of the red curves in Figure 8 and
9 are examples of distorted pan parameters. The con-
dition that the local zoom parameters s
l,x
and s
l,y
are
almost equal (see Equation 3), appears to hold also for
many obscured background (i.e. foreground) blocks.
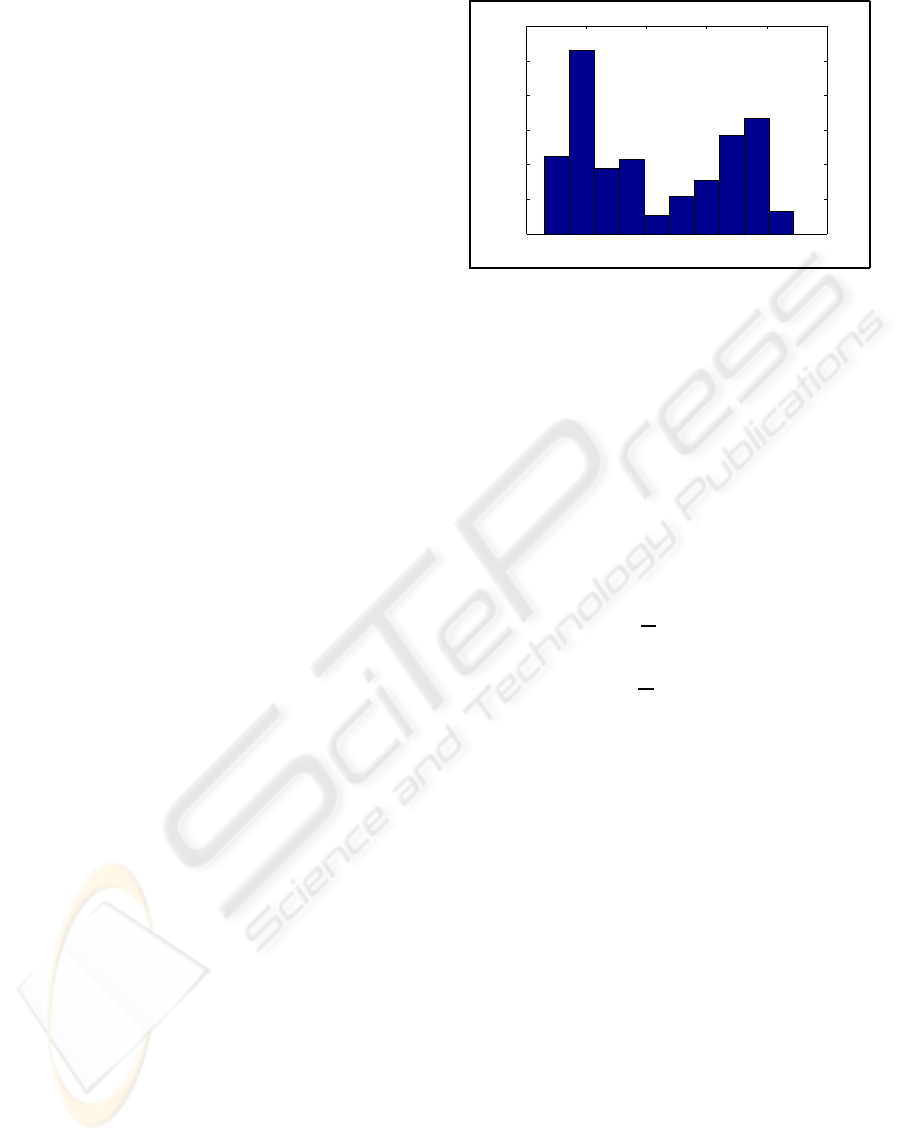
The histograms of the local pan parameters ex-
hibit several clusters in case of an obscured back-
ground area (see Figure 5 for an example). One or
more (in case of a histogram with many small bins) of
these clusters represents the local pan parameters of
the proper background blocks. The other clusters rep-
resent the local pan parameters of the obscured back-
ground blocks.
−5 0 5 10 15 20
0
20
40
60
80
100
120
Figure 5: Histogram of {p
l,x
} of an obscured background
area.
We use the previous global pan parameter
p
g
(t − 1) (the indices
x
and
y
are left out from now
on to indicate either case) to select the clusters cor-
responding to the proper background blocks, and to
compute the new global pan parameter p
g
(t) from
these clusters by the following procedure:
1. Estimate the probability density function
{pd f(p
k
)} and the cumulative density function
{cfd(p
k
)} for and from the sorted local pan
parameters {p
l
(t)} using Gaussian kernels
(Silverman, 1986):
pd f(p
k
) =
1
N
N
∑
i=1
G(p
k
; p
i
,s)
cfd(p
k
) =
1
N
N
∑
i=1
Z
p
k
−∞
G(p; p
i
,s)dp
(9)
with p
k
∈ {p
l
(t)}, p
i
≤ p
i+1
, N the number of lo-
cal pan parameters and G(p;µ,σ) the Gaussian
probability density function. We use the resolu-
tion of the motion vectors (1/8 pixel for our cases)
for the standard deviation s.
2. To eliminate noise valleys, local outliers in
{pd f(p
k
)} are replaced by the average of their
two neighbors (a kind of median filter). pd f(i)
(short for pd f(p
i
)) is a outlier on a rising flank
pd f(i− 2) ≤ pd f(i− 1)
pd f(i− 1) ≤ pd f(i+ 1)
pd f(i+ 1) ≤ pd f(i+ 2)
pd f(i− 2) < pd f(i+ 2)
(10)
if the following conditions are fulfilled:
pd f(i− 1) > pd f(i) ∨ pd f(i) > pd f(i+ 1)
|pd f(i) − pd f(i− 2)| ≤ t
outlier
|pd f(i) − pd f(i+ 2)| ≤ t
outlier
(11)
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
330

with the outlier threshold t
outlier
derived from the
absolute differences of the successive pd f values
{|pd f(i) − pd f(i− 1)|} as follows:
m = mean({|pd f(i) − pd f(i− 1)|})
s = std({|pd f (i) − pd f(i− 1)|} )
u = max({|pd f(i) − pd f(i− 1)|})
t
m,s
= m + s∗ Φ
−1
(0.99)
t
m,u
= (m+ u)/2)
t
outlier
= min(t
m,s
,t
m,u
)
(12)
Local outliers on a descending flank are detected
and replaced in a similar way.
3. Subdivide the refined {pd f(p
k
)} into clusters as
follows:
(a) Find the borders {b
l
,l ∈ [2,M − 1]} between
two clusters. The borders are placed at the val-
leys. A local pan parameter p
i
is a border if the
following conditions are fulfilled:
pd f(i) < pd f (i+ 1)
pd f(i) = {pd f(i− k),k ∈ [0, N],N ≥ 0}
pd f(i) < pd f (i− N − 1)
(13)
(b) Extend the set of borders by adding the smallest
local pan parameter p
1
and the greatest local
pan parameter p
N
to the sorted borders:
{p
1
,{b
l
,l ∈ [2,M − 1]}, p
N
} (14)
(c) Use these borders to create the cluster domains
{c
l
,l ∈ [1,M − 1]}:
c
l
= [b
l
,b
l+1
] (15)
(d) Remove ”insignificant” cluster domains. A
cluster domain c
k
is removed if both its pdf
peak and its pdf area are relatively small:
max(pd f(c
k
)) < f ∗ max({pd f (c
l
)})
cd f(c
k
) < f ∗ max({cd f(c
l
)})
(16)
with
cd f(c
i
) = cd f(b
i+1
) − cd f(b
i
) (17)
and
f =
N(2.0)
N(0.0)
≈ 0.1353 (18)
with N(x) the standard Normal probability den-
sity function.
Although this heuristic rule gives good results
for our video sequences, we are currently in-
vestigating whether this heuristic rule can be
replaced by a statistically based rule.
4. Compute for the final set of cluster do-
mains {c
l
,l ∈ [1,L]} the pan modus parameters
{pc
l
,l ∈ [1,L]}:
pc
l
= arg max(pd f(c
l
)) (19)
5. Use the previous global pan parameter p
g
(t − 1)
and the pan modus parameters {pc
l
,l ∈ [1,L]}) to
compute the new global pan parameter p
g
(t) as
follows:
p
g
(t − 1) ≤ pc
1
→ p
g
(t) = pc
1
(20)
pc
L
≤ p
g
(t − 1) → p
g
(t) = pc
L
(21)
pc
l
≤ p
g
(t − 1) < pc
l+1
→
p
g
(t) =
α
l
pc
l
+ α
l+1
pc
l+1
α
l
+ α
l+1
(22)
with
α
l
=
(pc
l+1
− p
g
(t − 1))
8
(pc
l+1
− pc
l
)
8
α
l+1
=
(pc
g
(t − 1) − pc
l
)
8
(pc
l+1
− pc
l
)
8
(23)
Because of the empirically determined exponent
8 for the coefficients α
l
and α
l+1
of the inter-
mediate case (see Equation 23), the new global
pan parameter p
g
(t) (see Equation 22) is approx-
imately equal to the pan modus parameter closest
to the previous global pan parameter p
g
(t − 1) ex-
cept when this previous global pan parameter is
located close to the center of the two pan modus
parameters (see Figure 6). Indeed, if the previ-
ous global pan parameter is far away from both
pan modus parameters, it is better to postpone the
choice for either of the two pan modus parame-
ters.
If there is one cluster left (i.e. L = 1), either Equa-
tion 20 or Equation 21 holds. In this case, inde-
pendent of the value of the previous global pan
parameter p
g
(t − 1), the new global pan parame-
ter p
g
(t) is equal to the pan modus parameter pc
1
of this cluster.
ROBUST ESTIMATION OF THE PAN-ZOOM PARAMETERS FROM A BACKGROUND AREA IN CASE OF A
CRISS-CROSSING FOREGROUND OBJECT
331

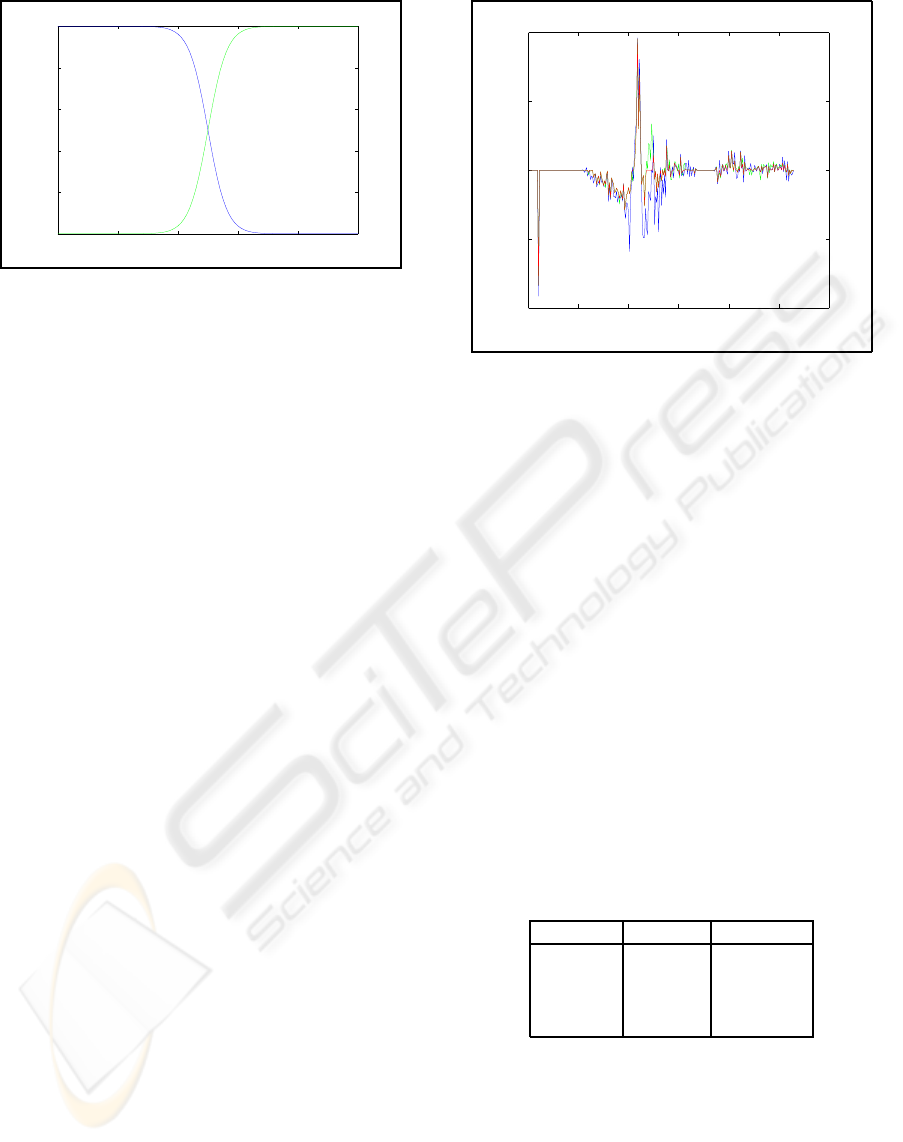
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
Figure 6: α
l
(blue) and α
l+1
(green) as function of the rel-
ative position of p
g
(t − 1).
Remarks:
1. We have first estimated the probability density
function {pd f (p
k
)} and the cumulative density
function {cf d(p
k
)} from the local pan parameters
{p
l
(t)} using the Gaussian mixture model with
a variable number of Gaussian pdf’s (Frederix,
2005). However, in some cases this method un-
derestimated the number of clusters.
2. If the first pair of frames of a shot contains an
obscured background area, real-time online selec-
tion of the proper pan modus parameters is not
possible because there are not yet reliable pan-
zoom parameters. But, if after a series of frames
a single cluster for the pan modus parameters
emerges, offline processing gives the possibility
to select the proper pan-zoom parameters of the
skipped frames by reversing the analysis of the
saved pan modus parameters from that frame back
to the beginning of the shot. Offline processing
gives even the possibility to select the proper pan
modus parameters when the whole shot contains
only multiple clusters by computation of the ”op-
timal” path through the pan modus parameters of
all frames of this shot.
5 RESULTS
We have applied both the EBA method (see Section
3) and the BAP method (see Section 4) to four video
shots, namely 50 frames (710x574) with a recording
of people passing a market stall with fruit (video shot
”FRUIT”), an arena shot with 326 frames (720x442)
of the movie ”The Gladiator” (video shot ”ARENA”),
an office shot with 266 frames (706x424) of the car-
toon ”Incredibles”(video shot ”OFFICE”) and a canal
chase shot with 52 frames (960x544) of the movie
”The Italian Job” (video shot ”CANAL”).
0 50 100 150 200 250 300
−0.02
−0.01
0
0.01
0.02
Figure 7: The global zoom parameter s
g,x
(blue), s
g,y
(green) and s
g
(red) for video shot OFFICE.
The global zoom parameters s
g,x
(blue curves), s
g,y
(green curves) and s
g
(red curves) for video shot OF-
FICE are shown in Figure 7. The negative peaks in the
neighborhood of frame 10 of video shot OFFICE are
caused by a shot cut. The three curves follow roughly
the same path. The use of the median for the global
zoom parameter s
g
(see Equation 7) results clearly in
less noise.
The first column of Table 1 contains the maximum
of the absolute differences between the global zoom
parameters max(|s
g,x
(t) − s
g,y
(t)|) at ˆx = 1. The sec-
ond column contains the same quantities at max( ˆx)
(i.e. at the side borders of the frame). The large differ-
ences for the video shots OFFICE and CANAL raise
the question whether a better method should be ap-
plied for the computation of the global zoom param-
eters from the local zoom parameters. We come back
to this issue in Section 6.
Table 1: max(|s
g,x
(t) − s
g,y
(t)|) in pixels.
shot at ˆx = 1 at max(ˆx)
FRUIT 0.00107 0.374
ARENA 0.00242 0.862
OFFICE 0.00981 3.414
CANAL 0.00657 3.154
For video shot FRUIT the maximum difference
between the pan parameters obtained with both meth-
ods was less than 1/8 pixel (the resolution of the mo-
tion vectors for our cases).
The distorted EBA (the red curves) and the im-
proved BAP (the green curves) pan parameters for
video shot OFFICE are shown in Figure 8 and 9.
There is an obscured background area roughly from
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
332

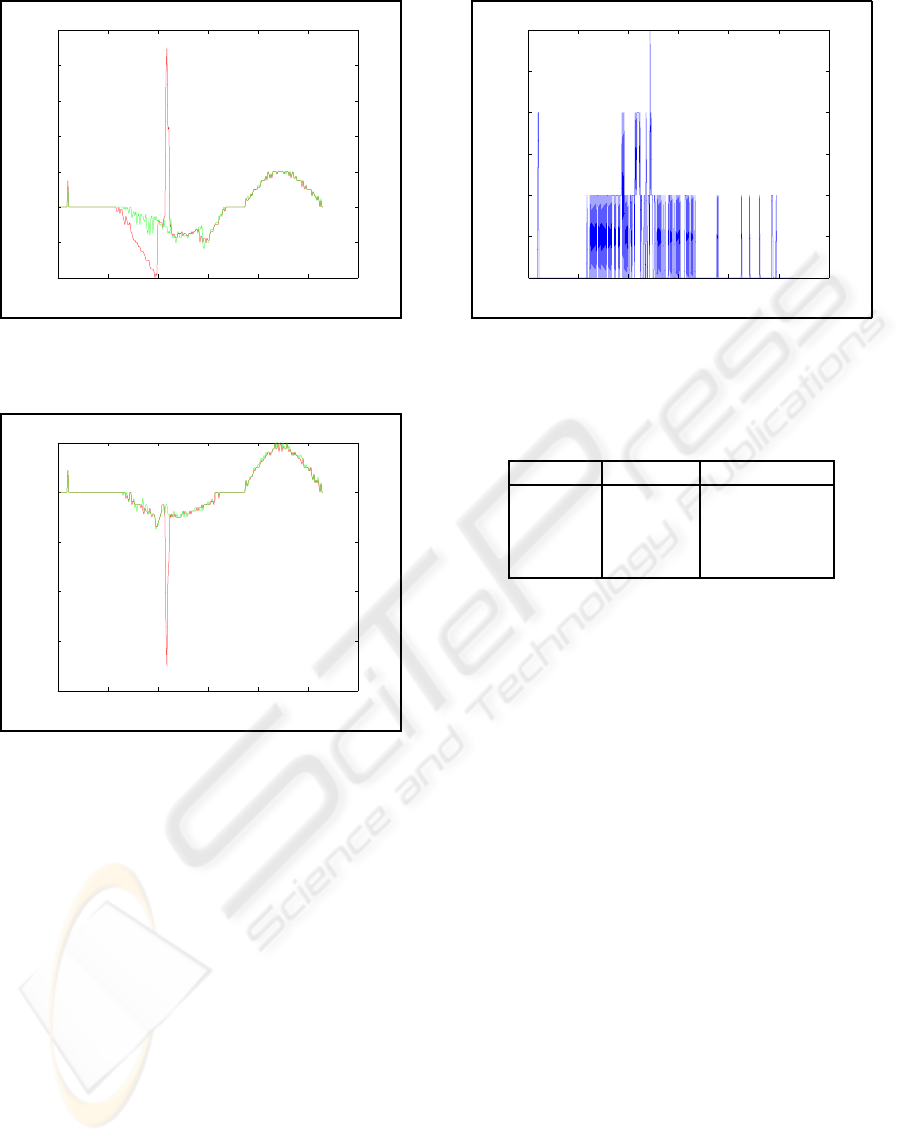
0 50 100 150 200 250 300
−4
−2
0
2
4
6
8
10
Figure 8: EBA (red) and BAP (green) pan parameter p
x
for
video shot OFFICE.
0 50 100 150 200 250 300
−8
−6
−4
−2
0
2
Figure 9: EBA (red) and BAP (green) pan parameter p
y
for
video shot OFFICE.
frame 50 until frame 150. The small peaks in the
neighborhood of frame 10 are caused by a shot cut.
Video shot CANAL gave similar results (more accu-
rate pan parameters for the BAP method)
The final number of clusters, alternating between
n
x
and n
y
, for video shot OFFICE are shown in Figure
10. There are clearly more clusters for the frameswith
an obscured background area.
The averaged elapsed time in milliseconds on a
Linux PC (2.8GHz Pentium 4) to estimate the pan-
zoom parameters for a frame with the EBA method
followed by the BAP method (without the time
needed for motion estimation) are given in the first
column of Table 2. The second column contains the
number of frames per second. Probably, most of the
computation time is spent in estimating the probabil-
ity density function (see Equation 9).
0 100 200 300 400 500 600
1
1.5
2
2.5
3
3.5
4
Figure 10: The final number of clusters for video shot OF-
FICE.
Table 2: The performance of the EBA method followed by
the BAP method.
shot milli-sec. #frames / sec.
FRUIT 49.6 20.2
ARENA 48.0 20.8
OFFICE 34.1 29.3
CANAL 67.8 14.7
6 CONCLUSIONS
1. The EBA method gives good results for shots with
a proper background area even if a small num-
ber of blocks is obscured by a foreground object
because outliers due to these blocks are excluded
from the final computation of the global zoom pa-
rameter.
2. The BAP method gives roughly the same results
for shots with a proper background area and much
better results for shots with an obscured back-
ground area than the EBA method.
3. We have inspected several histograms of the lo-
cal zoom parameters. The number of clusters for
these histograms was 1. But to increase the ro-
bustness of the BAP method, the same procedure
(i.e. cluster analysis and selection on the basis of
the previous parameters) should be applied also to
the computation of the global zoom parameters.
4. The current implementation of the BAP method
can be applied already for offline conversion, for
example in a media processor to convert a stored
2D video to a 2D+depth video to be stored on the
hard disk. After the offline conversion is finished
the stored 2D+depth video can be real-time ren-
dered on a 3DTV.
ROBUST ESTIMATION OF THE PAN-ZOOM PARAMETERS FROM A BACKGROUND AREA IN CASE OF A
CRISS-CROSSING FOREGROUND OBJECT
333

5. Because of the required amount of computation
time per frame, the current implementation of the
BAP method is not yet suitable for real-time 2D-
to-3D conversion. But the performance can and
will be improved (e.g. removal of code for in-
spection of the proper working of the algorithms).
REFERENCES
Armstrong, M. (1996). Self-Calibration from Image Se-
quences. PhD thesis, Department of Engineering Sci-
ence, University of Oxford, Oxford, UK.
Armstrong, M., Zisserman, A., and Hartley, R. (1996). Self-
calibration from image triplets. In Proc. ECCV, vol-
ume I, pages 3–16, Cambridge, UK.
Azarbayejani, A. and Pentland, A. (1995). Recursive esti-
mation of motion, structure, and focal length. IEEE
Trans. Pattern Anal. Machine Intell., 17(6):562–575.
Barenbrug, B. (2006). 3D throughout the video chain. In
Proc. IS&T ICIS’06, pages 366–369, Rochester, NY,
USA.
Beardsley, P., Torr, P., and Zisserman, A. (1996). 3D model
acquisition from extended image sequences. In Proc.
ECCV, volume II, pages 683–695, Cambridge, UK.
Berretty, R.-P., Peters, F., and Volleberg, G. (2006). Real-
time rendering for multiview autostereoscopic dis-
plays. In Proc. SPIE, Vol. 6055, 60550N, Stereoscopic
Displays and Virtual Reality Systems, pages 208–219,
San Jose, CA, USA.
de Beeck, M. O., Wilinski, P., Fehn, C., Kauff, P., Ijssel-
steijn, W., Pollefeys, M., van Gool, L., Ofek, E., and
Sexton, I. (2002). Towards an optimized 3D broadcast
chain. In Proc. SPIE, Vol. 4864, Three-Dimensional
TV, Video, and Display., pages 42–50, Boston, MA,
USA.
de Haan, G. and Biezen, P. (1994). Sub-pixel motion es-
timation with 3D recursive search block matching.
Signal Processing: Image Communication, 6(3):229–
239.
de Haan, G. and Biezen, P. (1998). An efficient true-motion
estimator using candidate vectors from a parametric
motion model. IEEE Trans. Circuits Syst. Video Tech-
nol., 8(1):85–91.
Ernst, F., Wilinski, P., and van Overveld, C. (2002). Dense
structure-from-motion: an approach based on segment
matching. In Proc. ECCV, LNCS 2531, pages 217–
231, Copenhagen, Denmark.
Falkenhagen, L. (1997). Block-based depth estimation
from image triples with unrestricted camera setup. In
Proc. IEEE Workshop on Multimedia Signal Process-
ing, pages 280–285, Princeton, New Jersey, USA.
Fehn, C. (2004). Depth-image-based rendering (DIBR)
compression and transmission for a new approach on
3D-TV. In Proc. SPIE, Vol. 5291, Stereoscopic Dis-
plays and Applications, pages 93–104, San Jose, CA,
USA.
Fehn, C., Kauff, P., de Beeck, M. O., Ernst, F., IJsselsteijn,
W., Pollefeys, M., van Gool, L., Ofek, E., and Sexton,
I. (2002). An evolutionary and optimised approach on
3D-TV. In Proc. IBC’02, pages 357–365, Amsterdam,
The Netherlands.
Frederix, G. (2005). Beyond Gaussian Mixture Models: Un-
supervised Learning with applications to Image Anal-
ysis. PhD thesis, Katholieke Universiteit of Leuven,
Belgium.
Hartley, R. and Zisserman, A. (2001). Multiple View Geom-
etry in computer vision. Cambridge University Press,
Cambridge, UK.
Huang, T. and Netravali, A. (1994). Motion and structure
from feature correspondences: A review. Proc. IEEE,
82(2):252–268.
Marazzi, A. (1987). Subroutines for robust estimation of lo-
cation and scale in ROBETH. Technical Report Cah.
Rech. Doc. IUMSP, No. 3 ROB 1, Institut Univer-
sitaire de Medecine Sociale et Preventive, Lausanne,
Switzerland.
Pollefeys, M. (1999). Self-Calibration and Metric 3D
Reconstruction from Uncalibrated Image Sequences.
PhD thesis, Katholieke Universiteit of Leuven, Bel-
gium.
Pollefeys, M., Koch, R., and van Gool, L. (1998). Self-
calibration and metric reconstruction in spite of vary-
ing and unknown internal camera parameters. In Proc.
ICCV, pages 90–95, Bombay, India.
Pollefeys, M., Koch, R., Vergauwen, M., Deknuydt, B.,
and van Gool, L. (2000). Three-dimensional scene
reconstruction from images. In Proc. SPIE, Vol. 3958,
Electronic Imaging, Three-Dimensional Image Cap-
ture and Applications III, pages 215–226, San Jose,
CA, USA.
Redert, P., Berretty, R.-P., Varekamp, C., van Geest, B.,
Bruijns, J., Braspenning, R., and Wei, Q. (2007).
Challenges in 3DTV image processing. In Proc. of
SPIE, Vol. 6508, Visual Communications and Image
Processing 2007, San Jose, CA, USA.
Silverman, B. (1986). Density Estimation for Statistics and
Data Analysis. Monographs on Statistics and Applied
Probability. Chapman & Hall, London, UK.
Xu, G. and Zhang, Z. (1996). Epipolar Geometry in Stereo,
Motion and Object Recognition. A Unified Approach.
Kluwer Academic Publishers, Dordrecht, The Nether-
lands.
Zhang, Z., Deriche, R., Faugeras, O., and Luong, Q.-T.
(1995). A robust technique for matching two uncal-
ibrated images through the recovery of the unknown
epipolar geometry. Artificial Intelligence Journal,
78(1-2):87–119.
VISAPP 2008 - International Conference on Computer Vision Theory and Applications
334