DIFFUSION FILTERING FOR ILLUMINATION INVARIANT FACE

RECOGNITION

Illumination Approximation with Diffusion Filters within Retinex Context

Peter Dunker and Melanie Keller

∗

Fraunhofer Institute for Digital Mediatechnology (IDMT), Ehrenbergstrasse 29, 98693 Ilmenau, Germany

Keywords:

Illumination normalization, face recognition, diffusion ﬁlter, diffusion tensor, retinex.

Abstract:

Face recognition becomes a very important technology in recent years for a lot of various applications. One

major problem of the most state-of-the-art algorithms are different lightning conditions which can decrease

recognition rates dramatically. To reduce the inﬂuence of illumination in the recognition process normaliza-

tion methods can be used. In this paper we introduce illumination normalization algorithms based on diffusion

ﬁlters. Further we compare our approaches with selected established algorithms. Finally we present our eval-

uation results based on well known face recognitions techniques and an appropriate face database. The results

show that the diffusion ﬁlter approaches outperforms all other algorithms which demonstrates the capabilities

of the diffusion ﬁlter technology for illumination normalization in face recognition.

1 INTRODUCTION

Face recognition is in the focus of challenging re-

search and besides a widely used technology in a mul-

titude of applications. However, there are still effects

that hinder the recognition process in most systems

dramatically e.g. varying facial expression or pose. In

this paper we focus on the problem of varying illumi-

nation.

Similar to (Gross and Brajovic, 2003) we concen-

trate on preprocessing techniques that do ”not require

any training steps, knowledge of 3D face models or

reﬂective surface models”. This type of preprocess-

ing algorithms ranges from simple histogram modiﬁ-

cations or local operations (Villegas-Santamaria and

Paredes-Palacios, 2005) up to elaborated human per-

ception inspired algorithms based on retinex theory

e.g. (Rahman et al., 1996).

Within this paper these algorithms are extended by

diffusion ﬁlter methods which are known from other

image processing task e.g. medical imaging (Westin

et al., 2002).

This paper is organized as follows. In section 2

we give a review of related algorithms. The use of

diffusion ﬁlter in image processing and especially for

illumination normalization is described in section 3.

∗

Corresponding author. Present address: Robert Bosch

GmbH, Daimlerstrasse 6, 71229 Leonberg, Germany

In section 4 we depict the used face recognition algo-

rithms and the database setup as well as the detailed

evaluation result. Finally conclusions are drawn form

the normalization performance.

Figure 1: The appearance difference caused by varying il-

lumination can be more then the appearance difference be-

tween two individuals (Adini et al., 1997). Figure is based

on Yale Face Database B (Georghiades et al., 2001).

2 BACKGROUND AND RELATED

WORK

In recent years a lot of different approaches for illu-

mination normalization in face recognitions were pre-

sented. In this section we simply focus on algorithms

that are related to the retinex theory. The retinex

model, named after retina and cortex, was introduced

by (Land, 1977) to explicate its model of the human

visual perception.

One of the most interesting points of the the-

ory is that the perceived intensity I(x, y) depends on

243

Dunker P. and Keller M. (2008).

DIFFUSION FILTERING FOR ILLUMINATION INVARIANT FACE RECOGNITION - Illumination Approximation with Diffusion Filters within Retinex

Context.

In Proceedings of the Third International Conference on Computer Vision Theory and Applications, pages 243-247

DOI: 10.5220/0001071302430247

 SciTePress

the reﬂection R(x, y) and the surrounding illumination

L(x, y) which can be calculated by the pixel neighbor-

hood.

I(x, y) = R(x, y)· L(x, y) (1)

Regarding to the idea that the perceived illumina-

tion depends on the neighborhood the following algo-

rithms try to estimate an illumination approximation

based on the pixel neighborhood of the image I.

The Single-Scale Retinex (SSR) introduced by

(Jobson and Woodell, 1995) deﬁnes a Gaussian ker-

nel to estimate the neighborhood illumination. Equa-

tion 2 with a single Gaussian (S = 1) can be used for

calculating SSR.

log(R(x, y)) =

∑

s=1

(log[I(x, y)] − log [I(x, y) ∗ G

(x, y)])

(2)

The Multi-Scale Retinex (MSR) extends the SSR

by using multiple Gaussian kernels (Rahman et al.,

1996). The aim of using different Gaussian ﬁlters

with varying σ

is a better approximation of the il-

lumination. The multiple results are combined by ac-

cumulating the single normalizations. Figure 2 shows

the results of SSR and MSR.

The next step to enhance the illumination esti-

mation with retinex methods is additionally consid-

ering the image structure. A ﬁrst step to more adap-

tive methods is made by (Wang et al., 2004) who in-

troduce the Self Quotient Image (SQI). Additional to

MSR the SQI weights the multiple Gaussian ﬁlters to

keep edges within the approximated illumination.

The most sophisticated algorithm is the illumi-

nation estimation according to Gross and Brajovic

(GBR) (Gross and Brajovic, 2003). It refers to We-

ber’s Law which describes the effect in human per-

ception that just noticeable difference of stimulus ∆I

depends on the previous stimulus I.

∆I

= ρ (3)

Instead of convolving with Gaussian ﬁlters the GBR

uses an minimization approach to estimate the illumi-

nation L.

E(L) =

Z Z

Ω

ρ(x, y) · [L(x, y) − I(x, y)]

dxdy

+ λ

Z Z

Ω

+ L

)dxdy

(4)

The weighting function ρ(x, y) is applied to handle the

local contrast ratio based on equation 3. The second

term of equation 4 describes a smoothing constraint

with λ as weighting factor.

The illumination approximations and the normal-

ized images of SQI and GBR are depicted in Figure 2.

Figure 2: Each of the retinex related algorithms calculates

an illumination estimations and afterwards a neutral illumi-

nated image. The SSR (a) produces the worst approxima-

tion because of the single gaussian. The illumination esti-

mation of the MSR (b) algorithm shows more details. The

SQI (c) and the GBR (d) results show much more edge sta-

bility on the facial contours whereas the GBR results seems

to be the best by visual impression.

3 DIFFUSION FILTER

APPROACH

The diffusion approach was introduced in image

processing as Scale-Space-Theory (SST) by (Witkin,

1983). In this theory image structures are handled at

different scales. Based on that fact images are pro-

cessed in single layers of a multi-resolutions pyramid

(Weickert, 1998). To generate the resolution pyramid

multiple Gaussian ﬁlters each for each layer can be

used.

I(x, y, t) = I(x, y) ∗ G(x, y, t) (5)

The varying parameter t yields to images of dif-

ferent resolution. Another form to describe that con-

text is the diffusion equation as used by (Koenderink,

1984):

∂

I = ∇

I = (I

+ I

) (6)

The work of Cohen and Grossberg about neu-

ral dynamics of brightness perception (Cohen and

Grossberg, 1984) shows that diffusion processes also

take place in human brightness perception. Feature

qualities like brightness are spread out diffusively to

boundary contours in visual cortex. Derived from this

theory any of the diffusion approaches can be used to

compute a illumination estimation L.

To combine two perceptional inspired algorithms

the illumination estimation based on diffusion is used

in this work in a illumination normalization process

according to the retinex theory, see equation 1.

To differ between diffusion algorithms we use the

following systematization by (Weickert, 1998).

• Linear isotropic diffusion: spread out to all direc-

tions without responding to edges

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

244

• Nonlinear isotropic diffusion: takes attention to

the intensity of edges

• Nonlinear anisotropic diffusion: takes attention to

the intensity and the direction of edges

The impacts on noisy images of different diffusion ﬁl-

ters are depicted in Figure 3. The disadvantage of the

SST is the linear isotropic behavior.

Figure 3: Different behaviors of diffusion ﬁlter for noise

reduction with attention to structured elements: a) origi-

nal, b) linear isotropic, c) nonlinear isotropic, d) nonlinear

anisotropic (Weickert, 1998).

For a nonlinear isotropic diffusion according to

the Weickert’s systematization we use the well-know

algorithm of (Perona and Malik, 1990) (PER). This

algorithm considers edges and reduces the diffusion

by a diffusion coefﬁcient c that depends on image gra-

dient intensity.

∂

I = ∇ · (c · ∇I) (7)

Additionally we introduce the usage of a ten-

sor based nonlinear anisotropic diffusion ﬁlter (TNS)

algorithm for illumination normalization. That ap-

proach uses a gradient direction related tensor D in-

stead of diffusion coefﬁcient c to weaken the diffusion

process.

The diffusion tensor D according to (van den

Boomgaard, 2004) is based on a rotation matrix and

can be measured as:

D =

)

+ (I

)



)

+ d

)

− d

)

+ d

)



(8)

Figure 4 shows the normalization results of the

PER and the TNS.

Figure 4: Illumination estimation and normalization results

for the different diffusion ﬁlter algorithm. a) PER illumi-

nation est., b) PER result, c) TNS illumination est., d) TNS

result. The PER and TNS show visual similar results with a

slightly better approximation by the TNS algorithm.

In general the PER resembles the GBR while PER

uses the gradient as weighting function and GBR the

Weber contrast.

4 EXPERIMENTS

To verify the power of the diffusion ﬁlter approaches

and for eased comparability with other publication

we choose well known recognition algorithms. Fur-

ther we evaluate with a database especially created

for varying illumination.

Face Recognition Algorithms. We use the eigen-

face (Turk and Pentland, 1991) and ﬁsherface (Bel-

humeur et al., 1997) approaches which are appearance

based subspace methods for face recognition. These

algorithms interpret pixels of images as coordinates

in a high-dimensional space and transform them into

low dimensional subspace called facespace. There-

fore a training process with observations of reference

persons is needed. For comparison within the faces-

pace the euclidic distance is used.

Because ﬁsherfaces were originally introduced as

more applicable for varying illumination we decided

to use both algorithms to compare improvements of a

varying illumination optimized and a non-optimized

algorithm. That means a well performing normal-

ization should produce similar results for both algo-

rithms.

Database. The database setup of our experiments

is as follows. We use the Yale Face Database B. It

is well suited for evaluation of lightning inﬂuence as

shown in (Georghiades et al., 2001). The database

consist of 45 images of 38 persons with a size of

192x168 pixels. The images of the same persons dif-

fer extremely by illumination but little in expression

and pose. Therefore it is possible to evaluate the illu-

mination normalization without further inﬂuence. We

use four of the already deﬁned subsets with similar

illumination conditions as shown in Figure 6.

In our experiments we used all possible combina-

tion of these subsets. This procedure is used to eval-

uate the very different conditions e.g. badly illumi-

nated training images and well illuminated test im-

ages and vice versa. Based on that procedure we get 4

by 4 recognitions rates as depicted in Table 1. Finally

we estimate the mean θ and the standard deviation σ

of the 16 sub results.

Results and Discussion. Table 1 shows exemplar-

ily the results of the TNS algorithm with eigenfaces.

The results clearly demonstrate that the best recog-

nition rates lie on the diagonal which means train

and test images were from the same subset but not

the same images. This shows that the recognition

algorithm after normalization is still sensitive to the

similarity in illumination of training and test data.

DIFFUSION FILTERING FOR ILLUMINATION INVARIANT FACE RECOGNITION - Illumination Approximation

with Diffusion Filters within Retinex Context

245

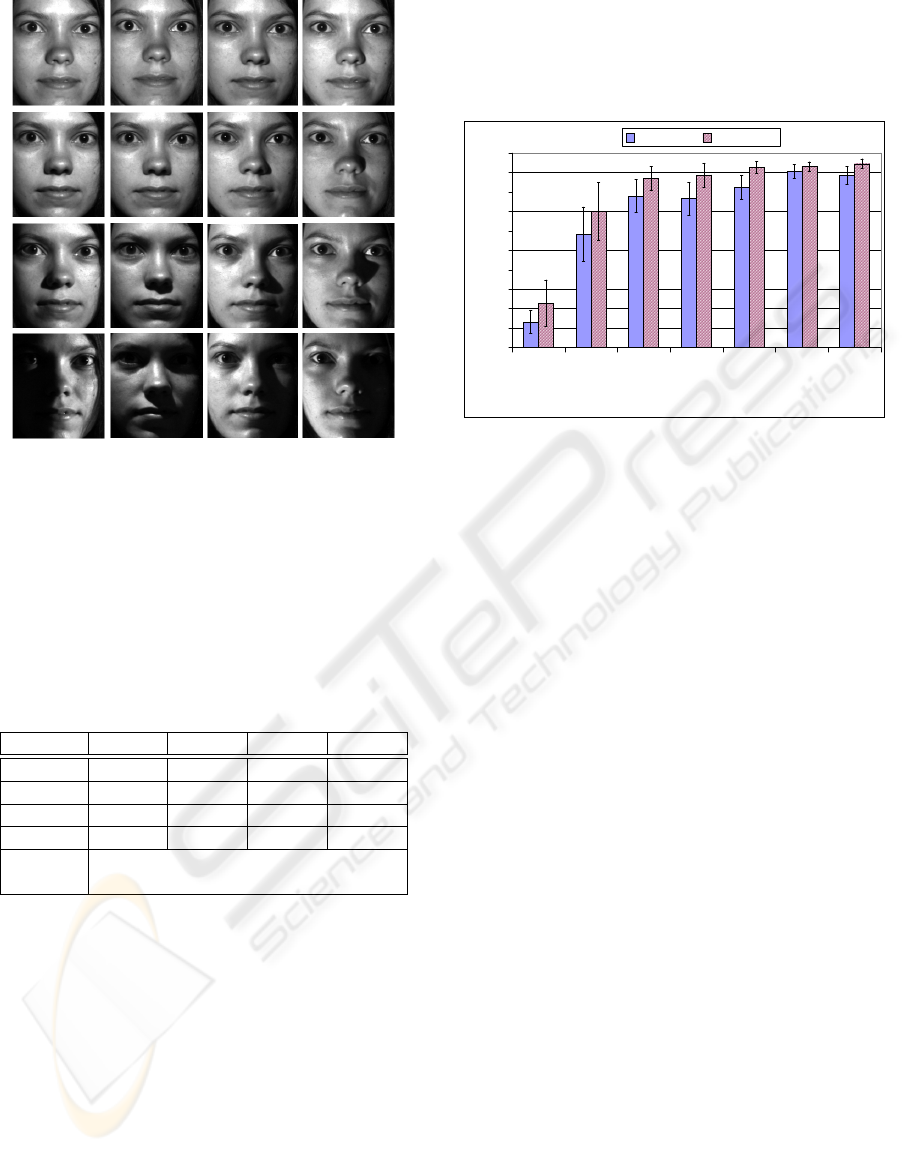
Figure 5: Examples of the Yale Face Database B subsets

which have similar illumination conditions within each sub-

set.

Hence the illumination impacts could not completely

removed. On the other hand the absolute values show

that usual varying illumination which can be found in

subset 1-3 can nearly perfect normalized so that the

overall result reaches 88,3 %.

Table 1: Evaluation results for the TNS algorithm with

eigenface recognition algorithm.

Test SS1 Test SS2 Test SS3 Test SS4

Train SS1 95,6 % 96,9 % 100,0 % 82,9 %

Train SS2 94,7 % 100,0 % 91,2 % 79,4 %

Train SS3 90,4 % 79,8 % 96,9 % 78,1 %

Train SS4 78,1 % 82,5 % 71,9 % 94,7 %

Final

88,3%

Final

9,2%

Figure 6 shows the recognition results of the dis-

cussed algorithms. The original dataset is the recog-

nition test without any normalization with results for

eigenface 13,2 % and ﬁsherface 22,7 %. This refer-

ence show already the better ability of the ﬁsherfaces

to handle worse illuminated images.

The SSR as worst algorithm in our evaluation

comes up with an improvement of about 45 % for

both recognition algorithm which is an enormous in-

creasing of the recognition rate. The MSR and SQI

algorithm results with similar recognition rates about

77 % for eigenface and about 87 % for ﬁsherface. The

improvement of the ﬁsherface via the eigenface is for

this normalization methods only about 7 % which is

little in comparison with the original dataset.

The best results of the prior algorithms produces

the GBR with 82,18 % and 92,63 %. This shows that

besides the best visual impression the GBR returns

also superior test results.

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

SSR

MSR

PER

Recognition Rate

Eigenface Fisherface

Figure 6: Evaluation results of all discussed algorithms for

eigenface and ﬁsherface recognition algorithm. The marked

deviations shows the standard deviation between the results

of the database subsets.

However, the diffusion ﬁlter algorithms outper-

forms all other algorithms. With PER 90,65 % and

92,9 % as well as TNS with 88,32 % and 94,41 %

each algorithm comes up with the best result for one

recognition algorithm. With 2,25 % difference the

PER algorithm comes up with the closest results be-

tween eigenface and ﬁsherface which indicates a con-

stant normalization.

The standard deviation of the results that can also

be used to measure the stability of the normalization

seems to be very close between the leading algorithm.

In principle it varies by the absolute mean values e.g.

TNS ﬁsherface σ 5 % and θ 94,41 % as well as SSR

ﬁsherface σ 29,66 % and θ 69,98 %.

Furthermore the results show clearly that the more

complex algorithm returns the best results. The com-

plexity of all algorithm increased by the consequent

use of human visual processing techniques based on

the perceptional concepts. Within this tests the use of

the diffusion tensor seems to be more applicable then

the Weber contrast used by the GBR.

5 CONCLUSIONS

In this paper we introduced the application of diffu-

sion ﬁlter algorithms for illumination invariant face

recognition. Further we presented the evaluation re-

sults of four retinex based algorithms and two diffu-

sion based methods. Within the evaluation we could

show that the single problem of illumination can be

handled very good by different algorithms. However,

VISAPP 2008 - International Conference on Computer Vision Theory and Applications

246

the novel used diffusion ﬁlter approaches could out-

perform the known algorithms with better and more

stable recognition results.

We showed also that the algorithms which are

closest to the visual perception could return the best

results.

Based on that ﬁrst evaluation results further inves-

tigation in diffusion ﬁlters for illumination normaliza-

tion is deﬁnitely reasonable. Especially the diffusion

tensor methods offer a lot of opportunities to improve

the recognition results.

ACKNOWLEDGEMENTS

Parts of the presented research were realized within an

ongoing partnership with the MAGIX AG. The pub-

lication was supported by grant No. 01MQ07017 of

the German THESEUS program.

REFERENCES

Adini, Y., Moses, Y., and Ullman, S. (1997). Face recog-

nition: The problem of compensating for changes in

illumination direction. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 19(7):721–732.

Belhumeur, P. N., Hespanha, J. P., and J.Kriegman, D.

(1997). Eigenfaces vs. ﬁsherfaces: Recognition us-

ing class speciﬁc linear projection. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

19(7):711–720.

Cohen, M. A. and Grossberg, S. (1984). Neural dynamics

of brightness perception: Features, boundaries, diffu-

sion, and resonance. Perception and Psychophysics,

36(5):428–456.

Georghiades, A. S., Belhumeur, P. N., and Kriegman, D. J.

(2001). From few to many: Illumination cone models

for face recognition under variable lighting and pose.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 23(6):643–660.

Gross, R. and Brajovic, V. (2003). An image preprocess-

ing algorithm for illumination invariant face recog-

nition. 4th International Conference on Audio- and

Video-Based Biometric Person Authentication, pages

10–18.

Jobson, D. J. and Woodell, G. A. (1995). Properties

of a center/surround retinex: Part 2 - surround de-

sign. Technical report, NASA Technical Memoran-

dum 110188.

Koenderink, J. (1984). The structure of images. Biological

cybernetics, pages 363–370.

Land, E. H. (1977). The retinex theory of color vision.

Scientiﬁc American, 237(6):108–120, 122–123, 126,

128.

Perona, P. and Malik, J. (1990). Scale-space and edge de-

tection using anisotropic diffusion. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

12(7):629–639.

Rahman, Z., Jobson, D. J., and Woodell, G. A. (1996).

Multi-scale retinex for color image enhancement. In-

ternational Conference on Image Processing.

Turk, M. A. and Pentland, A. P. (1991). Face recognition

using eigenfaces. IEEE Proceedings of Computer Vi-

sion and Pattern Recognition, pages 586–591.

van den Boomgaard, R. (2004). Geometry driven diffusion.

Lecture Notes at University of Amsterdam.

Villegas-Santamaria, M. and Paredes-Palacios, R. (2005).

Comparison of illumination normalization for face

recognition. Third COST 275 Workshop Biometrics

on the Internet, pages 27–30.

Wang, H., Li, S. Z., and Wang, Y. (2004). Face recognition

under varying lighting conditions using self quotient

image. Sixth IEEE International Conference on Auto-

matic Face and Gesture Recognition, pages 819–824.

Weickert, J. (1998). Anisotropic Diffusion in Image Pro-

cessing. Teubner-Verlag, Stuttgart.

Westin, C.-F., Maier, S., Mamata, H., Nabavi, A., Jolesz, F.,

and Kikinis, R. (2002). Processing and visualization

for diffusion tensor mri. In Medical Image Analysis,

Volume 6, Number 2, pages 93–108.

Witkin, A. P. (1983). Scale space ﬁltering. Proceedings In-

ternational Joint Conference on Artiﬁcial Intelligence,

pages 1019–1023.

DIFFUSION FILTERING FOR ILLUMINATION INVARIANT FACE RECOGNITION - Illumination Approximation

with Diffusion Filters within Retinex Context

247