STANDING JUMP LOFT TIME MEASUREMENT

An Acceleration based Method

Susana Palma, Hugo Silva, Hugo Gamboa

Plux – Biosensor Engineering, Lisbon, Portugal

Pedro Mil-Homens

Human Kinetics Faculty, Lisbon, Portugal

Keywords: Biomechanics, jump analysis, accelerometer, force platform, signal processing.

Abstract: This paper describes two methods for the measurement of loft time in vertical jumps using signals from an

acceleration sensor. The vertical jump accelerometer characteristic curve is presented and notable regions

corresponding to key stages of the kinetic activity are identified. Using the accelerometer signals along three

dimensions two different algorithms were devised to compute the loft time. These algorithms are based on

the morphology of the signal. The first uses the the maximum value of the curve during the landing stage;

the second uses the time interval between minimum and maximum values of the acceleration during the

flight and landing stages, respectively. To validate these algorithms, a standard algorithm to compute the

loft time from force platform signals was employed and these values taken as ground truth. Performance

assessment was performed by computing the relative errors between the loft time determined from the force

signal and the values obtained with each of the proposed approaches. Preliminary results for a set of 60

jumps let to relative errors of 7.0% for the first method and 2.9% for the second method.

1 INTRODUCTION

Vertical jumps are part of a variety of sports. In

athletic field vertical jump measurements are used

both to optimize and measure the performance of

various types of movements.

Performance of standing vertical jumps can be

accessed by measuring the time the athlete is in the

air – jump loft or flight time (Linthorne N. P., 2001).

The typical approach for measuring the loft time

uses force platform signals. With this approach the

jump must be performed while standing on the force

platform, that collects vertical force data. Force-time

curves contain kinetic and temporal information that

can be used to determine parameters that objectively

measure the performance of athletic movements

(Dowling, 1993). These platforms are rectangular

metal plates provided with force sensors and

connected by cabling to a data acquisition system

and computer. Due to their weight (ranging from

about 11 kg to 57 kg) and dimensions (usually

between 0.4 m × 0.6 m and 1.2 m × 1.2 m)

(amtiweb) the platforms are usually used only in

laboratory work, restrained the outside work by the

portability issues.

Acceleration data can be used to study the

characteristics of human movement (Hassan, M. R.,

2006) and assess parameters that identify one's state

of physical activity. In jumping studies, acceleration

signals are also an important source of information.

In this paper we present two different algorithms for

determining vertical jumps loft times using a three

axial accelerometer. In this case, the portability

issues are lessened because the accelerometer and

the acquisition system employed are light-weighted

wireless devices.

The two algorithms were applied to a set of 60

vertical jumps and validated with a standard

algorithm for computation of loft time from force

platform signals.

Like on the vertical force curve, six interest

regions can be identified on the acceleration-time

curve: rest, preparation, take-off, flight, landing. and

recovery. Following the last stage a rest period can

also be present. Figure 1 shows the vertical force

393

Palma S., Silva H., Gamboa H. and Mil-Homens P. (2008).

STANDING JUMP LOFT TIME MEASUREMENT - An Acceleration based Method.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 393-396

DOI: 10.5220/0001069203930396

 SciTePress

and acceleration signals acquired during a vertical

squat jump.

Figure 1: Stages of a vertical squat jump.

Some key points can be identified on the

acceleration signal that are characteristic of the

different stages of the jump and that are repeated as

a pattern when a series of jumps is acquired. The

biggest oscillations of the signal are noticed at the

beginning of the flight stage and the landing stage -

when the jumper leaves the ground and when his

feet first contact the ground after the flight,

respectively. A recovery phase follows the landing.

During this period of time the acceleration oscillates

and converges to its rest value which is reached

when the jumper finishes the jump. The fact that the

flight stage is clearly demarcated on the force curve

is usually used to compute the duration of the flight

– loft time. As we can see in Figure 1, the

acceleration curve has also characteristic features

that can be related with the loft time. Two of these

features were used in this work to estimate the

duration of the flight stage.

2 MATERIALS

The experimental set-up consisted of a bioPlux8

wireless electrophysiological data acquisition system

(Silva, H., 2005, plux.info) to which we connected a

xyzPlux triaxial accelerometer and a force platform

(AMTI- LG 6-4-2000). With this apparatus force

and acceleration (along three dimensions) were

synchronously recorded during the vertical standing

jumps.

The accelerometer was placed at the jumper's

low back on the skin surface (Figure 2). The force

platform signal was used for result comparison.

Figure 2: Placement of the accelerometer at the jumper's

low back skin.

3 METHODS

The methodology for determining the flight time

was based on the morphological analysis of the

acceleration curves of a set of 60 jumps.

Figure 3: Acceleration and force curves of a series of 3

vertical jumps.

By comparing the acceleration curve of a set of

jumps with the respective vertical force curve

(Figure 3) we observe that some of the acceleration

curve characteristic features seem to be related with

the duration of the flight stage, namely at the flight

and landing stages. Using notable points of these

stages we devised two different algorithms to

compute the loft time. The average acceleration

curve was determined from the acceleration signals

of the three dimensions and low passed using a

moving average filter using a window of 250 points

(Proakis J. G.,1995). Each of the algorithms uses

different measurements of time and amplitude taken

from this signal.

The first algorithm uses the landing stage curve

amplitude (Figure 4). This stage is characterized by

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

394

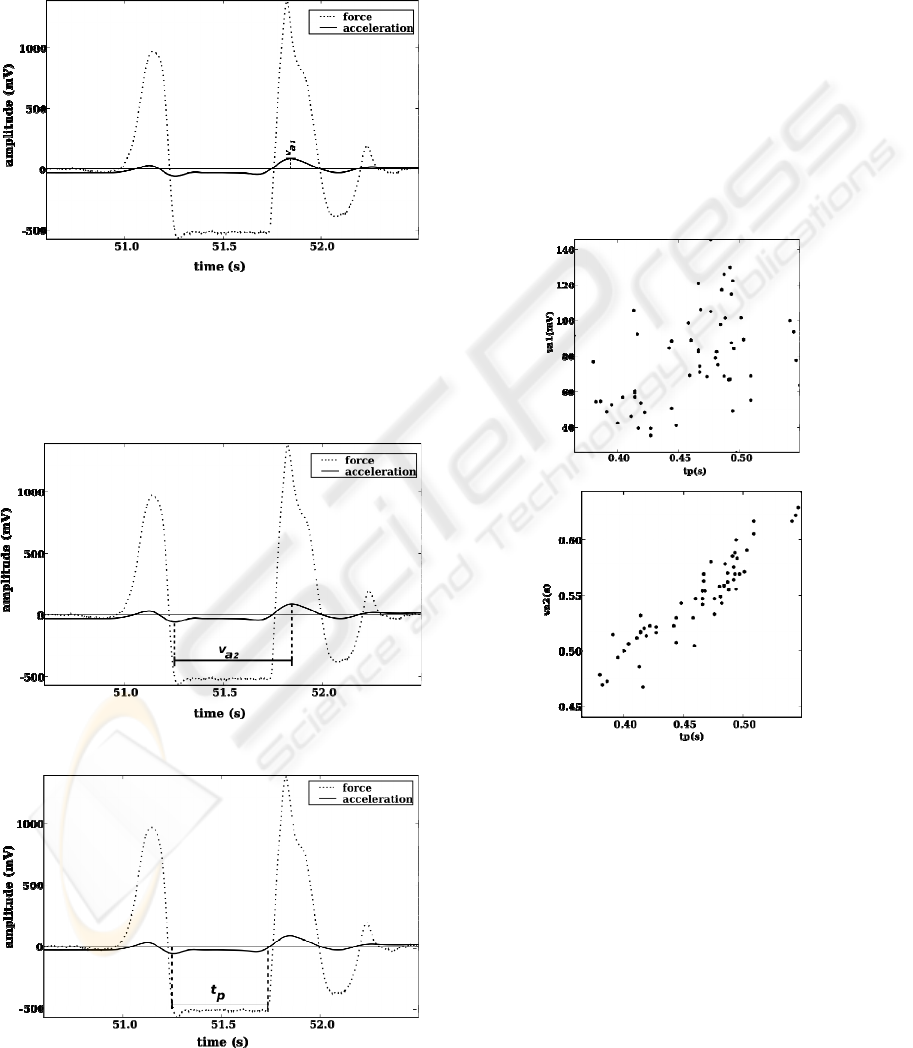
sharp variations of the acceleration signal due to the

vibration of the accelerometer when the feet first

contact the force platform on the landing. The low-

passed signal obtained from the smoothing still

preserves this impact peak whose amplitude (v

)

was measured and used as a predictor variable for

the loft time.

Figure 4: Jump parameter used on the first algorithm.

The second algorithm determines the time

interval between the minimum of the smoothed

signal on the flight stage and the impact peak. With

this algorithm, a direct measure of the loft time is

obtained (Figure 5).

Figure 5: Jump parameter used on the second algorithm.

Figure 6: Jump parameter used by the standard algorithm.

For result comparison purposes, we determined

the jump loft time of the 60 jumps from the force

platform signal and took these values as ground

truth. A standard algorithm was employed that

computes the time during which the jumper is not

touching the force platform - the time interval

between the take-off and landing instants - where the

force signal has a negative plateau (Figure 6).

4 RESULTS

The two independent variables measured on the

acceleration signal (v

) were plotted against the loft

time determined from the force platform signal (t

The scattergrams of these two variables are shown in

Figure 7.

(a)

(b)

Figure 7: Scattergrams of the loft time measured with the

standard algorithm versus (a) the variable measured with

algorithm 1 and (b) the variable measured with algorithm

A high correlation between the loft time

measured from the force platform signal and the

time interval measured from the acceleration curve

) can be seen is Figure 7b. This is a much better

predictor of the flight time than the amplitude of the

landing stage impact peak (r=0.382 and r=0.933

respectively). The regression equations for both

variables are given by (1) and (2):

STANDING JUMP LOFT TIME MEASUREMENT - An Acceleration based Method

395

104,102106,406

−−

×× +v=t

a1p1

(s)

(1)

0,0680,967

−

a2p2

v=t (s)

(2)

Using these equations we can obtain estimates of

the loft time (t

) from the variables measured from

the accelerometer signal (v

The loft time relative error associated with each

of the algorithms i was determined for each jump j

(δ

εij

), taking as “real” loft times the values measured

from the force platform signal(t

(

)

1,2 1,... 60

jij

δ =,i=;j=,

−

(3)

The accuracy of the algorithms was assessed by

determining the corresponding average loft time

relative errors:

εi

∑

εij

,i= 1,2 j=1,..., 60

(4)

The results led to relative errors of 7,0% for the

first algorithm and 2,9% for the second algorithm

Taking as reference the mean loft time determined

for the set of 60 jumps with the regression equations

(1) and (2) these relative errors correspond to 32 ms

and 13 ms, respectively.

Both algorithms are also affected by a common

base error of 0.1% which is characteristic of the

acquisition unit and inversely proportional to its

sampling rate.

Usually, when the force platform is used to

determine the loft time an associated error of 0,5% is

introduced because the algorithm is susceptible of

the parameters chosen by the user as the initial and

final points of the flight stage. In contrast, the

algorithms we propose are automatic.

5 CONCLUSIONS

The time interval between the minimum acceleration

value of the flying stage and the maximum

acceleration value of the landing stage is the best of

the two devised measures, showing a good

correlation with the real loft times (r=0.933 and

.=2,9%).

Although associated with errors, these

preliminary results indicate that these algorithms are

good alternative methods for the computation of loft

time, taking advantage of the use of an

accelerometer instead of a force platform, which is

more expensive and less portable.

In addition to the flight time other parameters

used to assess the performance of the jump can be

found on the acceleration signal, such as the height

of the jump. Furthermore, information on the

dynamic behaviour of the jumper, namely during the

flight stage can also be obtained from the

acceleration signal, which is impossible to study

with only the vertical force signal.

In the future, we plan to study the load

distribution between inferior members during the

take-off and landing stages by combining

acceleration and force analysis and study the on-

flight behaviour of the jumper.

REFERENCES

Dowling J., Vamos, L., 1993, J., Identification of Kinetic

and Temporal Factors Related to Vertical Jump

Performance, Applied Biomechanics, 9.

Linthorne, N. P., 2001, Analysis of standing vertical jumps

using a force platform, Am. Journal of Phys., 69 (11).

Hassan R., Begg R. K., Khandoker A. H., Stokes R., 2006,

Automated Recognition of Human Movement in Stress

Situations, Proceedings of the 2

Internationsl

Workshop on Biosignal Procesing and Classification –

BPC 2006, INSTICC Press.

Silva H., Gamboa H., Viegas V., Fred A., 2005, Wireless

Physiologic Data Acquisition Platform., 2005.

Proceedings of the 5

Conference on

Telecomunications Confele.

http://www.plux.info

http://www.amtiweb.com/bio/force_platforms.htm

Proakis J. G., Manolakis D., 1995, Digital Signal

Processing: Principles, Algorithms and Applications,

Pearson US Import & PHIPEs, 3

International

Edition.

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

396