
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL
ACOUSTIC ARRAYS
Douglas L. Jones, Michael E. Lockwood, Albert S. Feng and Bruce C. Wheeler
Beckman Institute, University of Illinois at Urbana-Champaign, 405 N. Mathews, Urbana, IL, USA
Keywords:
Beamforming, hearing aids, biologically inspired beamformers, cocktail party.
Abstract:
Many biological hearing systems perform much better than existing signal processing systems in natural set-
tings. Two biologically inspired adaptive beamformers, one mimicking the mammalian dual-delay-line local-
ization system, show SNR gains in challenging cocktail-party scenes substantially exceeding those of con-
ventional adaptive beamformers. A “zero-aperture” acoustic vector sensor array inspired by the parasitoid
fly Ormia ochracea and accompanying algorithms show even better performance in source recovery than the
binaural beamformers, as well as the ability to localize multiple nonstationary sources to within two degrees.
New experimental studies of the performance of the biologically inspired beamformers in reverberation show
substantial reduction in performance in reverberant conditions that hardly affect human performance, thus
indicating that the biologically inspired algorithms are still incomplete.
1 INTRODUCTION
Many biological hearing systems exhibit remarkable
performance that greatly exceeds that of current en-
gineered systems. An example is the parasitoid fly,
Ormia ochracea, which orients toward its cricket prey
to within two degrees by use of an ear about a mil-
limeter in maximum extent (Robert et al., 1996). The
dominant frequency of the cricket’s call is about 5
kHz, so Ormia achieves this remarkable accuracy
with an aperture that is well less than 1/50th of a
wavelength, and at a range exceeding that of cricket
females. Ormia thus exceeds the traditional Rayleigh
resolution by well more than an order of magnitude.
The human hearing system also demonstrates re-
markable performance in many respects. With only
two ears, it achieves lateral directional accuracy simi-
lar to Ormia and considerable ability to localize com-
plex natural sounds in elevation as well. Its ability
to recover a desired speech source in the presence of
multiple simultaneous speech interferers (the “cock-
tail party” environment) with only two ears is un-
equaled by conventional signal processing methods;
current beamforming or source-separation algorithms
fail when the number of sources exceeds the number
of sensors. The human hearing system is also remark-
ably tolerant to reverberation and time-varying envi-
ronments.
For comparison, consider that conventional engi-
neered beamforming systems require a many-element
array of about half-wavelength spacing between el-
ements to achieve the high directional accuracy
demonstrated by Ormia. An array of at least as many
sensors as sources, again with an appropriateaperture,
would be required to perform acceptable signal recov-
ery at a cocktail party in an anechoic chamber; tens
of elements would be required to accomplish this in
the presence of the modest reverberation in a typical
room.
Clearly, the performance of these biological sys-
tems far exceeds that of current electronic systems,
at least for their specific biological application. By
drawing ideas and inspiration from these systems,
we have developed new algorithms that greatly ad-
vance the state-of-the-art in acoustic signal recov-
ery of speech and similar natural systems in com-
plex real-world environments. These new methods
show promise for many applications, including hear-
ing aids, hands-free telephony in noisy or reverberant
environments, and surveillance.
2 CONVENTIONAL BINAURAL
BEAMFORMERS
Acoustic beamforming for hearing aids presents a
special challenge because the total aperture on a sin-
gle behind-the-ear (BTE) array is well less than two
centimeters. This is well below half a wavelength for
128
L. Jones D., E. Lockwood M., S. Feng A. and C. Wheeler B. (2008).
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL ACOUSTIC ARRAYS.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 128-135
DOI: 10.5220/0001068801280135
Copyright
c
SciTePress

the audio frequencies with most speech energy; ar-
rays of only two, or at most three, microphones can be
used, and resolution well beyond the Rayleigh limit is
required for significant directionality.
The minimum-variance distortionless response
(MVDR) (also known as linearly constrained mini-
mum variance (LCMV)) methodology introduced by
Capon (Capon, 1969) is the most common approach
for super-resolution adaptive beamforming. MVDR
beamformers minimize the output energy of the best
linear combination of the microphone inputs, subject
to the constraint that any signal from the desired tar-
get (or “look” direction) is exactly preserved. The
minimum-energy objective causes maximal rejection
of unwanted sources from other directions or noise,
while the distortionless response constraint prevents
the beamformer from attenuating or otherwise dis-
torting the desired signal. The distortionless-response
constraint is captured in a “steering” vector, e, which
represents the relative magnitudes and phases of a sig-
nal from the target look direction, and the linear con-
straint equation on the beamformer weights, w
opt
, is
e
H
w
opt
= 1. Capon derived the constrained optimal
linear weights for scalar (instantaneous mixing or nar-
rowband signals) beamforming:
w
opt
=
R
−1
e
e
H
R
−1
e
(1)
Capon’s method has several major limitations.
The beamformer will work successfully only if the
number of interfering sources is less than the num-
ber of sensors. It requires accurate knowledge of
the steering vector; errors in e cause the beamformer
to cancel the desired signal as well as the interfer-
ence. The super-resolution capability of Capon’s
beamformer also amplifies this problem, because
even small errors can be sufficient to allow self-
cancellation. In particular, any reverberation mani-
fests itself in this frameworkas a single source with an
altered, composite steering vector; self-cancellation is
usually so severe as to render Capon’s adaptive beam-
former unusable in hearing aids. Finally, Capon’s
original approach applies only to narrowband sources
or instantaneous mixtures.
Frost (Frost III, 1972) and later Griffiths and Jim
(Griffiths and Jim, 1982) overcame this last limita-
tion by applying the Capon MVDR criterion to beam-
formers with filters, rather than just scalar, weights on
each array channel. These algorithms avoid the com-
putational complexity and numerical instability of in-
verting large matrices by applying the LMS algorithm
to iteratively convergetoward the optimal constrained
filter weights. Griffiths’ and Jim’s GSC algorithm is
generally used for wideband adaptive beamforming,
and several attempts have been made to apply it to di-
rectional or binaural hearing-aid arrays. In carefully
controlled laboratory settings with a single interferer,
it has shown considerable gain, but with additional
interferers or even modest reverberation, the perfor-
mance collapses, often producing a negative signal-
to-noise (SNR) gain.
Figure 3 summarizes the performance of a care-
fully optimized GSC beamformer in anechoic condi-
tions for speech recovery in the presence of one, two,
three, and four speech interferers from different di-
rections in the front half-plane. (Use of Greenberg’s
adaptive step-size was essential to avoid misconver-
gence during intervals of silence in the target speech
and to obtain positive SNR gain (Greenberg, 1998).)
As can be seen in the figure, the beamformer per-
forms well for a single interference, but the perfor-
mance drops dramatically when the total number of
sources exceeds the number of sensors. For appli-
cations such as hearing aids that are limited to two
or three microphones and must perform well in the
cocktail-party context, the conventional beamforming
approach is inadequate.
3 BIOLOGICALLY INSPIRED
BINAURAL BEAMFORMERS
The GSC beamformer performance is perfectly con-
sistent with beamforming theory, but psychophysi-
cal studies, as well as the personal experience of ev-
ery human being with normal hearing, show that hu-
mans perform much better in the cocktail-party en-
vironment. Using only two ears, humans can local-
ize as many as six simultaneous sources (Bronkhorst
and Plomp, 1992) and gain a very significant binau-
ral advantage in terms of ability to understand a de-
sired speech source among multiple spatially sepa-
rated interferers. Clearly, biology holds some secrets
unknown to engineering for improved performance
with small arrays in crowded acoustic environments
for speech sources.
3.1 A Biologically Inspired Beamformer
The remarkable performance of the human binau-
ral hearing system in the cocktail-party environment
has prompted us to develop new biologically inspired
beamforming algorithms. The mammalian hearing
system has been extensively studied by physiologists;
while a great deal remains to be deciphered, much
is now known. Mammals’ brains use several cues
to determine direction, including the interaural time
difference (ITD), which is equivalent to phase delay
for narrowband signals, interaural intensity (or level)
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL ACOUSTIC ARRAYS
129
difference (IID), and spectral shaping for elevation
(Yost and Gourevitch,1987). The cochlea act as filter-
banks that separate the signals at each ear into differ-
ent frequency bands, which are processed in parallel.
Based on physiological studies that have located and
identified the specific neural circuitry, Jeffress (Jef-
fress, 1948) modeled the mammalian interaural time-
difference mechanism as a dual delay-line circuit as
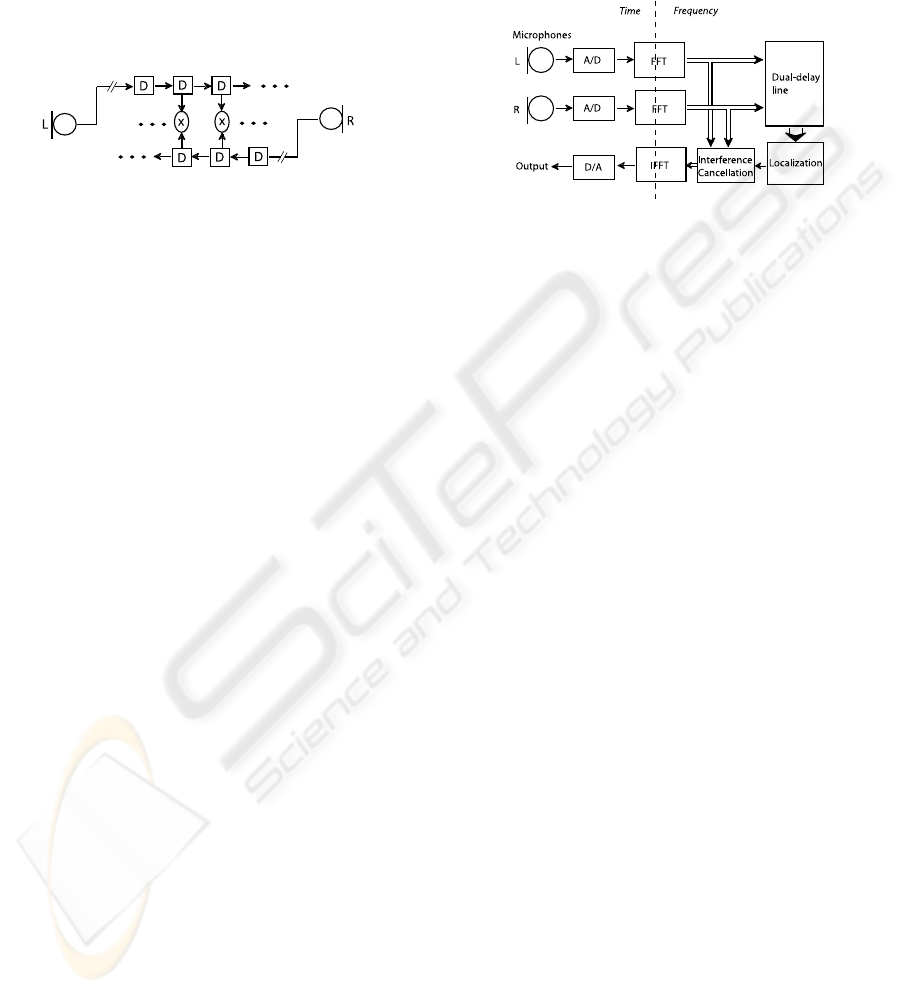
illustrated in Figure 1.
Figure 1: The mammalian interaural time-delay dual delay-
line circuit.
The neural response to the sound passes, in oppo-
site directions and in parallel for each frequency band,
through counter-flowing delay lines. The signals at
corresponding positions in the delay lines are in effect
cross-correlated over short time intervals, and the de-
lay yielding the peak coincidence produces a strong
response, indicating a dominant source in the corre-
sponding direction at that frequency and time. It is
less well understood how higher stages of the neural
processing use this information.
Based on this model, we developed a biologically
inspired binaural beamforming algorithm with much
better performance in the cocktail-party scenario than
the conventional GSC. Following the mammalian
ITD system, the method in Liu et al. (Liu et al., 2000)
transforms the signal to the short-time frequency do-
main via an overlapped FFT filter-bank (this differs
somewhat from mammalian ears, in which the filter
bandwidths vary across frequency). Independently at
each frequency and delay-line pair, a running short-
time sum-of-absolute-differences (SAD) is computed
to create a frequency-delay map of the strength of co-
incidence. The neural system sharpens the directional
responses via inhibition of weaker neighboring re-
sponses; the algorithm mimicks this by locating local
peaks and thresholding to create a binarized, sparse
map of the dominant signal directions as a function of
both frequency and direction. For broadband sources
such as speech, integrating this map across frequency
provides a composite graph that clearly indicates the
directions of several simultaneous sources active at
that time. The peaks in this composite directional map
are thresholded to determine the number and direction
of all significant active sources. This completes the
“localization” step of the method.
The desired source is recovered, or “extracted”
from the interference, via guided frequency-domain
null-steering beamforming (Liu et al., 2001). The
source (as identified from the localization step) clos-
est in direction to that of the target is recovered by ap-
plying a different constrained beamformer in each fre-
quency band that passes the desired source and nulls
the dominant interferer in that band. Figure 2 illus-
trates the method.
Figure 2: A block diagram of the biologically inspired lo-
calization/extraction beamformer.
Liu et al. report excellent performance; for four
simultaneous speech sources in an anechoic environ-
ment, intelligibility weighted SNR gains ranged from
8 to 9.1 dB (Liu et al., 2001). The SNR gain ranged
from 4.6 to 6.7 dB in a test room with a reverberation
time of 0.4 sec. These performances far exceed that
of the conventional GSC beamformer for such condi-
tions.
3.2 A DSP-friendly Biologically
Inspired Beamformer
While closely resembling the biological system, the
localization/extraction method described above is
computationally expensive when implemented on a
conventional electronic computer. The characteristics
of neural systems (massively parallel and relatively
slow) and current electronic hardware (much less par-
allel and extraordinarily fast) differ enough that di-
rect mapping of the neuronal algorithm to electronics
may not be the most effective engineering solution.
Accordingly, we developed an alternate biologically
inspired algorithm that captures some of the essen-
tial features of the mammalian hearing system while
being much more amenable to real-time DSP imple-
mentation.
The mammalian auditory system exhibits key
characteristics, exploited by the biologically inspired
algorithm, that allows its excellent performance. The
mammalian hearing system processes auditory sig-
nals within frequency bands and dynamically over
short-time intervals; that is, it performs some type
of rapidly adapting time-frequency processing. It is
essential to note that the mammalian auditory sys-
tem is not designed for the narrowband signals or
white Gaussian noise for which most signal process-
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
130
ing algorithms are optimized; such signals are rare in
natural environments. The signals, and the interfer-
ence, of most relevance to humans are transients and
speech, which are rapidly time-varying, have consid-
erable harmonic structure, and are relatively sparse
in time-frequency. For example, even continuous
speech has many short intervals of silence, and speech
has formants, at many times strong harmonic struc-
ture (voiced speech), and other distinct and relatively
sparse structure in frequency as well. In the short-
time-frequency domain, the average number of inter-
ferers in any time-frequency bin is much less than
the number of sources. Thus, while beamforming
theory shows that only fewer interferers than sen-
sors can be cancelled for narrowband frequency or
broadband noise sources, with frequency decomposi-
tion and rapid adaptivity, the inherent time-frequency
sparseness can be exploited to cancel most of several
“simultaneous” interferers.
With this biologically inspired insight, new ap-
proaches better matched to implementation with cur-
rent DSP hardware can be derived that still demon-
strate performance approaching that of the more bi-
ologically faithful algorithm of Liu et al. Time-
frequency decomposition to expose the sparsity of the
sources and interferers, and rapid adaptation to take
advantage of it, are the key elements that allow a
binaural system to overcome multiple interferers in a
cocktail-partyenvironment. We havedevelopeda par-
ticular frequency-domain MVDR beamformer imple-
mentation (FMV) that provides similar interference
rejection and is easily implementable in a low-power,
fixed-point, real-time DSP system such as a digital
hearing aid (Lockwood et al., 2003). Like the L/E al-
gorithm described earlier, the algorithm begins with
overlapped short-time FFTs of the individual input
channels, and subsequently processes each channel
independently. This exposes the time-frequency spar-
sity of the interference. This transformation produces
the added advantage that the beamformers in each
frequency bin are scalar. Running short-time cross-
correlation matrices are computed at each frequency
via an efficient recursive update. In most frequency-
domain MVDR implementations, the GSC algorithm
is used to slowly adapt the beamformer due to the
O(N
3
) complexity and stability challenges of the ma-
trix inverse. However, for a binaural beamformer, im-
plemented in the frequency domain, N = 2 in each in-
dependent channel, and direct solution for the optimal
Capon weights according to (1) requires only a few
operations after algebraic simplification. We also ap-
ply a multiplicative (energy-normalized) regulariza-
tion to provide some robustness to the short-time cor-
relation estimates (Cox et al., 1987). Just as in the
first algorithm, the optimal beamforming weights are
applied at each frequency and the extracted signal of
interest is recovered via an inverse FFT.
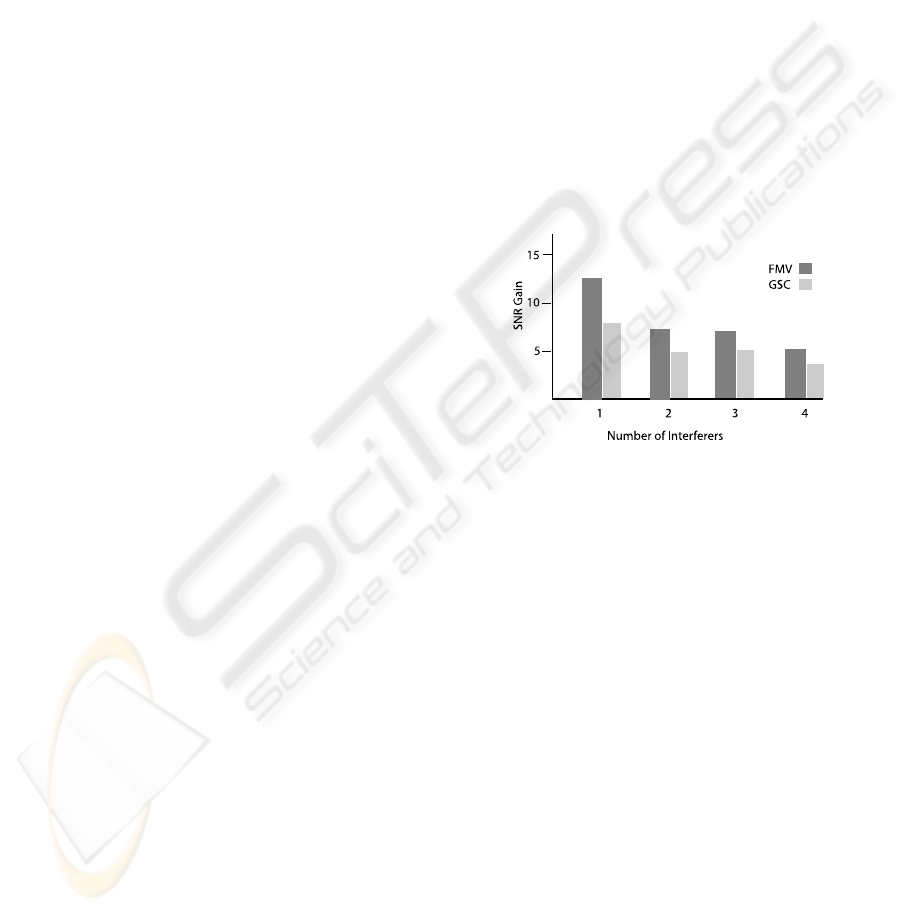
Figure 3 shows the performance in terms of SNR
gain of a 15 cm two-element free-field array in an
anechoic environment with one through four interfer-
ers. The initial SNR for the desired source was about
-3 dB, representing a challenging cocktail-party sit-
uation at about the lower threshhold at which peo-
ple with normal hearing can follow conversational
speech. Each of these conditions summarizes many
runs with at least four different configurations of po-
sitions of the interferers (the target was always po-
sitioned at broadside, or perpendicular to the line of
the array), and at least eight combinations of differ-
ent male and/or female talkers for each configuration.
For comparison, the performance of our best imple-
mentation of the conventional GSC beamformer is
also shown. As is clear from the figure, the perfor-
Figure 3: SNR gains for one, two, three, and four simulta-
neous speech interferers of the FMV (dark) and GSC (light)
adaptive beamformers.
mance of the biologically inspired FMV beamformer
substantially exceeds that of the GSC, particularly (as
expected) for cases with more than one simultaneous
interferer. The FMV algorithm’s performance may be
somewhat inferior to the L/E method (which is too
expensive to perform the complete battery of tests for
direct comparison), but FMV clearly captures some
of the strengths of the biological system. The slow
convergence of the LMS-based iterative GSC adap-
tation prevents it from reacting fast enough to ex-
ploit the time-frequency sparseness of the interfer-
ence. (Each test is only 2.4 seconds long and both
beamformers are initialized to a conventional sum-
ming beamformer, so GSC’s somewhat inferior per-
formance even for one source also reflects slower
convergence. For one source and after convergence,
the performance of both beamformers is compara-
ble.) The results strongly suggest that the FMV beam-
former, like the L/E method, has captured at least one
of the special “tricks” that the human hearing sys-
tem uses to perform well with only two ears in the
cocktail-party context.
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL ACOUSTIC ARRAYS
131

4 BIOLOGICALLY INSPIRED
BEAMFORMING WITH A
ZERO-APERTURE ArrAy
Miles et al. have found that Ormia ochracea ob-
tains its amazing directional accuracy of less than two
degrees with an ear about a millimeter across by a
precise mechanical coupling of the common (omni-
directional) and differential modes of oscillation be-
tween the left and right sections of the ear (Miles
et al., 1995). A unique connecting structure with pre-
cise mechanical tuning causes even slightly off-center
sound direction to induce much larger vibrations in
the nearer ear-plate. Inspired by this system, Miles
and collaborators are developing single-chip silicon
MEMS arrays of two orthogonal differential and one
omni-directional microphones (Miles et al., 2001),
each only slightly larger than Ormia’s ear. The total
aperture of this array is only a few millimeters on a
side. An array with a similar acoustic response but in
all three dimensions can be constructed out of three
gradient (figure-8 pattern) hearing-aid microphones
arranged orthogonally in three dimensions (X,Y, and
Z axes) and one omni-directional microphone to form
an acoustic vector sensor with a total extent of well
less than a centimeter in any dimension (see (Lock-
wood and Jones, 2006) for a photograph of such an
array used for the experiments reported below.)
The relative gains of a signal from direction θ and
elevation φ on the three directional (X,Y, and Z) and
one omni-directional (O) microphones are
g
O
= 1 (2)
g
X
= cos(θ)cos(φ) (3)
g
Y
= sin(θ)cos(φ) (4)
g
Z
= sin(φ) (5)
and are unique for any arrival direction. Since this
array requires no spatial separation to distinguish the
direction of arrival, is small, and the microphones are
located right next to each other, we colloquially refer
to this as a “zero-aperture” array.
4.1 Super-Resolution Direction-Finding
With a Zero-Aperture Array
A unique mechanical structure combines the common
(omni) and differential (directional gradient) modes
of Ormia’s ear to form a highly directional response.
Inspired by this remarkable biological system, we
can combine these modes electronically to form a
super-resolution beamformer. While Capon’s MVDR
beamformer is usually applied to spatially separated
arrays with equal gains and for which relative phase
differences between elements distinguishes the source
direction, Capon’s formulation applies as well to am-
plitude and phase or amplitude-only differences in di-
rectional response, a fact which has been exploited
in underwater acoustic vector sensor arrays (Nehorai
and Paldi, 1994) (D’Spain et al., 1992), and which
has been shown to improve the performance of the
FMV binaural beamformer on the head (Lockwood
and Jones, 2006).
For narrowband or broadband noise sources, the
MVDR beamformer can only localize fewer sources
than sensors. Many engineering applications may re-
quire more, so we havecombined the biological inspi-
rations of Ormia’s directional microphone array and
the mammalian hearing system to develop a method
for doing so. With the acoustic vector sensor array,
we imitate the interaural level difference system in
the mammalian brain. As described above, the mam-
malian system exploits the time-frequency sparsity
of natural sources to localize more sources than sen-
sors by identifying the locations of sources in time-
frequency bins in which only one source dominates.
Mohan et al. have developed a signal-processing-
friendly approach for achieving the same goal (Mo-
han et al., 2003a) (Mohan et al., 2003b). As in
the FMV algorithm described earlier, the inputs from
all microphones are short-time Fourier transformed
and cross-correlated within each frequency band. A
sinple rank test is performed on each short-time-
frequency correlation matrix to estimate the number
of significant sources in that bin. Any bin of full
rank (equal or more sources than sensors) is ignored;
any bin of lower rank (more sensors than sources)
can be used to estimate the direction of its dominant
sources. To each low-rank bin we apply either an
MVDR or MuSIC (Schmidt, 1986) beamformer us-
ing the directional array responses in (2), (3), (4), (5)
to form the steering vectors, and form a composite
localization map by summing (usually with normal-
ization) these individual high-resolution directional
maps. The number of sources and their locations are
then determined in the usual manner by finding and
threshholding the peaks of this composite response.
In both simulation and with real data, this al-
gorithm achieves directional accuracy comparable to
Ormia (less than two degrees of error variance) and
locates more sources than sensors (Mohan et al.,
2003a). It can be applied to, and performs similarly
with, binaural arrays (Mohan et al., 2003b).
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
132
4.2 Speech Source Recovery With a
Zero-Aperture Array
The Ormia-inspired acoustic vector sensor array can
also be combined with the FMV algorithm for higher
performance speech source recovery in the cocktail-
party scenario with a much smaller aperture than even
the binaural array. Since Capon’s formulation sup-
ports steering vectors with direction-dependent am-
plitude, as well as phase, differences, FMV can be ap-
plied almost without modification other than forming
steering vectors according to the relative responses of
the directional microphones in the target direction.
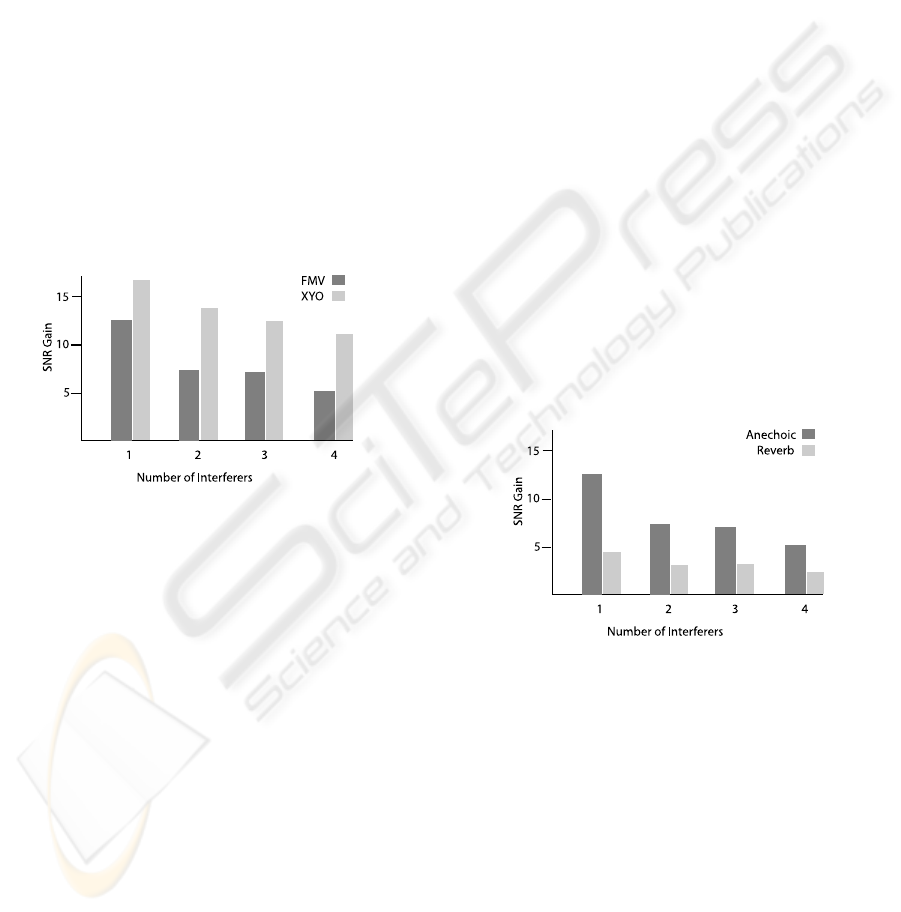
Figure 4 shows the performance in terms of SNR
gain of a 15 cm two-element free-field array in an
anechoic environment with one through four interfer-
ers. The physical experiments from which these data
are created are identical to those used to create Figure
3. Since all sources were in the horizontal plane, we
used only three microphones, the X and Y directional
microphones and the omni.
Figure 4: SNR gains for one, two, three, and four simulta-
neous speech interferers of binaural and XYO arrays with
the FMV adaptive beamformer.
The performance of the FMV beamformer with
the XYO microphone array is considerably better than
with the binaural array. We believe that this is mainly
because the relative difference in the response of the
directional microphones is relatively independent of
frequencyand is greater at the lower frequencies com-
prising most of the speech signal energy; at these
frequencies, the separation of the binaural array is
much less than half a wavelength, and separation of
the sources becomes progressivelymore difficult. The
extra microphone may also play a lesser role.
5 ADAPTIVE BEAMFORMER
PERFORMANCE WITH
REVERBERATION
The human hearing system performs well in com-
plex natural environments, which usually include at
least modest, and sometimes quite substantial, rever-
beration. As described earlier, adaptive beamform-
ing algorithms are particularly sensitive to reverbera-
tion, which alters the effective steering vectors of the
source. This makes the desired source appear to come
from a different direction, and the super-resolution
interference suppression of the adaptive beamformer
then allows it to cancel the target even if these errors
are small. It is essential to evaluate our biologically
inspired algorithms, which only capture some of the
features of the complex biological system, for their
robustness to the reverberation found in typical lis-
tening situations.
Figure 5 shows the performance of the binaural
beamformer in the presence of reverberation for the
same set of tests shown above. The “anechoic” steer-
ing vectors were obtained by measuring impulse re-
sponses from microphones near the center of a sound-
treated room and truncating these after the initial re-
sponse was complete and before arrival of the first
reflections. The steering vectors thus capture the re-
sponse of the microphones and recording electronics
but not the room. The impulse responses in multiple
rooms, such as typical and large conference rooms
and offices, were measured at various distances at
fifteen-degree increments, to allow the synthesis of
many realistic scenes with various positions and num-
bers of interferers.
Figure 5: SNR gains for one, two, three, and four simultane-
ous speech interferers of the FMV beamformer in anechoic
and reverberant conditions.
Figure 5 shows the performance in terms of SNR
gain for the FMV algorithm in a typical medium-sized
conference room, with a reverberation time (T
60
) of
less than 0.4 seconds, for target and interfering speech
sources at a 1 meter distance, at which the direct
sound substantially exceeds the reverberation. Even
in these relatively benign conditions, the performance
of the beamformer, while still positive, drops dramat-
ically in the presence of reverberation. The reduced
performance even with a single interferer indicates
that it is mostly due to mismatch of the steering vec-
tor for the target source, rather than changes in the
response to the interferers; other tests too numerous
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL ACOUSTIC ARRAYS
133

to describe here support this diagnosis. Humans per-
form as well or even slightly better under conditions
of modest reverberation compared to anechoic condi-
tions, so this performance loss is due to limitations of
the algorithm rather than the intrinsic difficulty of the
problem.
Robust beamforming methods attempt to over-
come this problem. Cox, et al. show that several
criteria for robustness are optimized by regulariza-
tion of the correlation matrix in Capon’s formula-
tion (Cox et al., 1987). This has the effect of con-
trolling self-cancellation for small deviations in the
steering vector, but at the price of reducing the in-
terference suppression. Many other methods have
been introduced that minimize the worst-case perfor-
mance or introduce additional constraints to prevent
self-cancellation over an uncertainty region, but again
these methods sacrifice interference cancellation to
obtain robustness. As mentioned earlier, the human
hearing system’s performance has been shown to im-
prove somewhat with modest reverberation, which in-
dicates that it works on very different principles. We
speculate that it learns, adapts to, and exploits the ac-
tual room response, thus avoiding the trade-off be-
tween performance and robustness of current signal-
processing approaches. We are currently working on
practical techniques to do the same.
6 CONCLUSIONS
The excellent performance of the biologically in-
spired binaural adaptive beamformers with more
speech sources than microphones strongly suggests
that the biologically inspired algorithms capture some
of the essential features of the mammalian hearing
system that allow humans to perform so well in these
conditions. These key elements are exploitation of the
time-frequency sparseness of natural source signals
via short-time frequency decomposition and rapid,
separate adaptation in each band to take maximal ad-
vantage of it. Similarly, the comparable performance
in directional localization accuracy of the binaural
algorithm based on the Jeffress auditory model to
that of humans, as well as that of the acoustic vec-
tor sensor array of collocated directional microphones
with that of the parasitoid fly Ormia ochracea, sug-
gests that these localization algorithms have identified
some of the key principles of the biological systems.
The substantial degradation in performance of the
FMV beamformer with levels of reverberation easily
tolerated by humans suggests, on the other hand, that
key features of human auditory processing of great
importance to real-world application are missing from
the model. Preliminary evidence that the localization-
extraction method (which is based more directly on
the physiological model) degrades less under rever-
berant conditions may eventually yield some hints as
to what is missing. Current robust beamforming algo-
rithms tolerate reverberation by limiting the damage
to performancedue to errors in the steering vector (of-
ten at substantial sacrifice to performance under good
conditions); biological systems, on the other hand,
seem to adapt to and even exploit the real-world con-
ditions. We are currently exploring new strategies for
robust beamforming that attempt to learn and exploit
the variations in response introduced in real-world
conditions, with the ultimate goal of building algo-
rithms approaching the remarkable robustness shown
by biological signal processing systems.
The characteristics of biological and electronic de-
vices are very different, particularly in terms of com-
plexity of function, parallelism, and speed, so the
best biologically inspired signal processing systems
may involve different implementations at the “hard-
ware” level. We thus believe that biological inspira-
tion, based on discernment of the underlying phys-
ical or signal processing principles exploited by the
biological system, usually yields better results than
biological imitation. However, physiology only in-
directly indicates the signal processing principles ex-
ploited by the auditory sensors and the brain, so the
development of effective and efficient biologically in-
spired signal processing algorithms is rarely straight-
forward. Close collaboration between physiologists,
psychophysicists, and signal processors can yield in-
sights and ultimately signal processing systems that
would be difficult to conceive individually.
ACKNOWLEDGEMENTS
We gratefully acknowledge the research support
of the Mary Jane Neer Foundation, Phonak USA,
Inc., the National Institutes of Health NIH-NIDCD
1R01DC005782-01A1, DARPA DAAD17-00-0149,
and the National Science Foundation ITR CCR-
0312432.
REFERENCES
Bronkhorst, A. and Plomp, R. (1992). Effect of multiple
speechlike maskers on binaural speech recognition in
normal and impaired hearing. Journal of the Acousti-
cal Society of America, 92:3132–3139.
Capon, J. (1969). High-resolution frequency-wavenumber
spectrum analysis. Proceedings of the IEEE,
57(8):1408–1418.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
134

Cox, H., Zeskind, R., and Owen, M. (1987). Robust adpa-
tive beamforming. IEEE Trans. Acoust., Speech, Sig-
nal Processing, 35(10):1365–1376.
D’Spain, G., Hodgkiss, W., Edmonds, G., Nickles, J.,
Fisher, F., and Harriss, R. (1992). Initial analysis of
the data from the vertical DIFAR array. Proc. Mast.
Oceans Tech.(Oceans. 92), pages 346–351.
Frost III, O. (1972). An algorithm for linearly constrained
adaptive array processing. Proceedings of the IEEE,
60(8):926–935.
Greenberg, J. (1998). Modified LMS algorithms for
speech processing with an adaptive noise canceller.
IEEE Transactions on Speech and Audio Processing,
6(4):338–351.
Griffiths, L. and Jim, C. (1982). An alternative ap-
proach to linearly constrained adaptive beamforming.
IEEE Transactions on Antennas and Propagation],
30(1):27–34.
Jeffress, L. (1948). A place theory of sound localization. J.
Comp. Physiol. Psychol, 41(1):35–39.
Liu, C., Wheeler, B., O.Brien Jr, W., Bilger, R., Lansing, C.,
and Feng, A. (2000). Localization of multiple sound
sources with two microphones. Journal of the Acous-
tical Society of America, 108:1888.
Liu, C., Wheeler, B., O.Brien Jr, W., Lansing, C., Bilger, R.,
Jones, D., and Feng, A. (2001). A two-microphone
dual delay-line approach for extraction of a speech
sound in the presence of multiple interferers. Journal
of the Acoustical Society of America, 110:3218.
Lockwood, M. and Jones, D. (2006). Beamformer perfor-
mance with acoustic vector sensors in air. Journal of
the Acoustical Society of America, 119:608.
Lockwood, M., Jones, D., Bilger, R., Lansing, C.,
O.Brien Jr, W., Wheeler, B., and Feng, A. (2003).
Performance of time-and frequency-domain binau-
ral beamformers based on recorded signals from real
rooms. Journal of the Acoustical Society of America,
115:379.
Miles, R., Gibbons, C., Gao, J., Yoo, K., Su, Q., and
Cui, W. (2001). A silicon nitride microphone di-
aphragm inspired by the ears of the parasitoid fly
Ormia ochracea. Journal of the Acoustical Society of
America, 110:2645.
Miles, R., Robert, D., and Hoy, R. (1995). Mechanically
coupled ears for directional hearing in the parasitoid
fly Ormia ochracea. Journal of the Acoustical Society
of America, 98:3059.
Mohan, S., Lockwood, M.E., Jones, D.L., Su, Q., and
Miles, R.N. (2003). Sound source localization with
a gradient array using a coherence test. Journal of the
Acoustical Society of America, 114(4 pt. 2):2451.
Mohan, S., Kramer, M., Wheeler, B., and Jones, D. (2003).
Localization of nonstationary sources using a coher-
ence test. IEEE Workshop on Statistical Signal Pro-
cessing, pages 470–473.
Nehorai, A. and Paldi, E. (1994). Acoustic vector-sensor
array processing. IEEE Transactions on Signal Pro-
cessing, 42(9):2481–2491.
Robert, D., Read, M., and Hoy, R. (1996). The tympa-
nal hearing organ of the parasitoid fly Ormia ochracea
(Diptera, Tachinidae, Ormiini). Cell and Tissue Re-
search, 275(1):63–78.
Schmidt, R. (1986). Multiple emitter location and signal
parameter estimation. IEEE Trans. Antennas Propag,
pages 276–280.
Yost, W. and Gourevitch, G. (1987). Directional hearing.
Springer-Verlag New York.
BIOLOGICALLY INSPIRED BEAMFORMING WITH SMALL ACOUSTIC ARRAYS
135
