TOWARDS A UNIFIED MODEL FOR THE RETINA

Static vs Dynamic Integrate and Fire Models

Pedro Tom´as, Jo˜ao Martins and Leonel Sousa

INESC-ID / IST TU Lisbon, Rua Alves Redol 9, 1000-029, Lisboa, Portugal

Keywords:

Retina Models, Stochastic Leaky Integrate and Fire, Poisson-based model, Dynamic model.

Abstract:

Many models have been proposed to describe the visual processing mechanisms in the retina. The spike

generation mechanism of the models is typically performed by a Poisson process. Alternatively, a more

realistic approach can be used by implementing an integrate and ﬁre mechanism. In this paper we show

that the Stochastic Leaky Integrate and Fire (SLIF) model is equivalent to a non-linear Poisson-based model.

Furthermore, it proposes a dynamic model for the retina visual processing path, achieved through modulations.

For estimating this model a two-step approach is proposed: i) an initial estimation is computed by using a

spike-triggered analysis, and ii) the likelihood of the spike train is maximised by gradient ascent.

1 INTRODUCTION

Vision is a fundamental sense in one’s everyday life

that gained even more relevance in the modern soci-

ety; most of the information, art and entertainment re-

lies on it. A continuously growing number of research

groups have been dedicating their efforts to help visu-

ally impaired people by developing visual prostheses

capable of conveying some kind of vision; a endeav-

our which demands the development of accurate and

reliable retina models.

Retinal ganglion cells respond to visual stimuli by

eliciting spikes whenever the inner-membranevoltage

potential surpasses a given threshold. This response,

y(t), is characterised by the time spikes occurred; it

can be mathematically represented as a sum of Dirac

functions δ(t−t

) centred at the time instantst

, when

the inner-membrane voltage potential surpassed the

threshold: y(t) =

∑

δ(t − t

Several retina models, based mainly on general

neuron models, have been proposed. Two of the most

typical are the Poisson based model (Chichilnisky,

2001) and the Stochastic Leaky Integrate and Fire

(SLIF) (Paninski, 2006) model. However, in this pa-

per it is shown that, under some constraints, they

are equivalent. Moreover, a dynamic model is pro-

posed based on developed mathematical machinery

used to prove the equivalencebetween these two mod-

els. This dynamic model modulates its output not

only by the stimulus characteristics but also by the

recent spike ﬁring history. To estimate this model’s

parameters several other issues are addressed, such as

the tuning and initialisation of this model, where it is

used spike-triggered analysis. At the end some exper-

imental results are provided.

This paper is organised as follows. Section 2

shows the equivalence between the SLIF model and

a Poisson based model. Section 3 presents the pro-

posed dynamic model and describes its tuning. Some

experimental results are drawn in Section 4, and sec-

tion 5 concludes the paper.

2 STOCHASTIC INTEGRATE

AND FIRE MODEL

A typical approximation for the Hodgkin and Hux-

ley neuron model assumes a leaky integrate and ﬁre

model. By adding a noise component to the model,

it is possible to simulate the variability of real neu-

rons (Keat et al., 2001). For a linear ﬁrst order in-

tegrate and ﬁre mechanism, the SLIF model is de-

scribed by the stochastic differential equation (SDE):

dv(t) = −

v(t)dt + i(t)dt + σξ(t) (1)

where τ is a constant variable, ξ(t) is standard white-

noise and σ is a multiplicative term which deﬁnes the

power of the noise source. The above SDE is valid un-

til the subthreshold potential surpasses a given thresh-

old V

. Whenever this happens a spike is ﬁred and

the neuron enters a refractory period where no spike

can be ﬁred. Accordingly with the SLIF model, at the

end of this period, which typically lasts a couple of

528

Tomás P., Martins J. and Sousa L. (2008).

TOWARDS A UNIFIED MODEL FOR THE RETINA - Static vs Dynamic Integrate and Fire Models.

In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 528-533

DOI: 10.5220/0001067905280533

 SciTePress

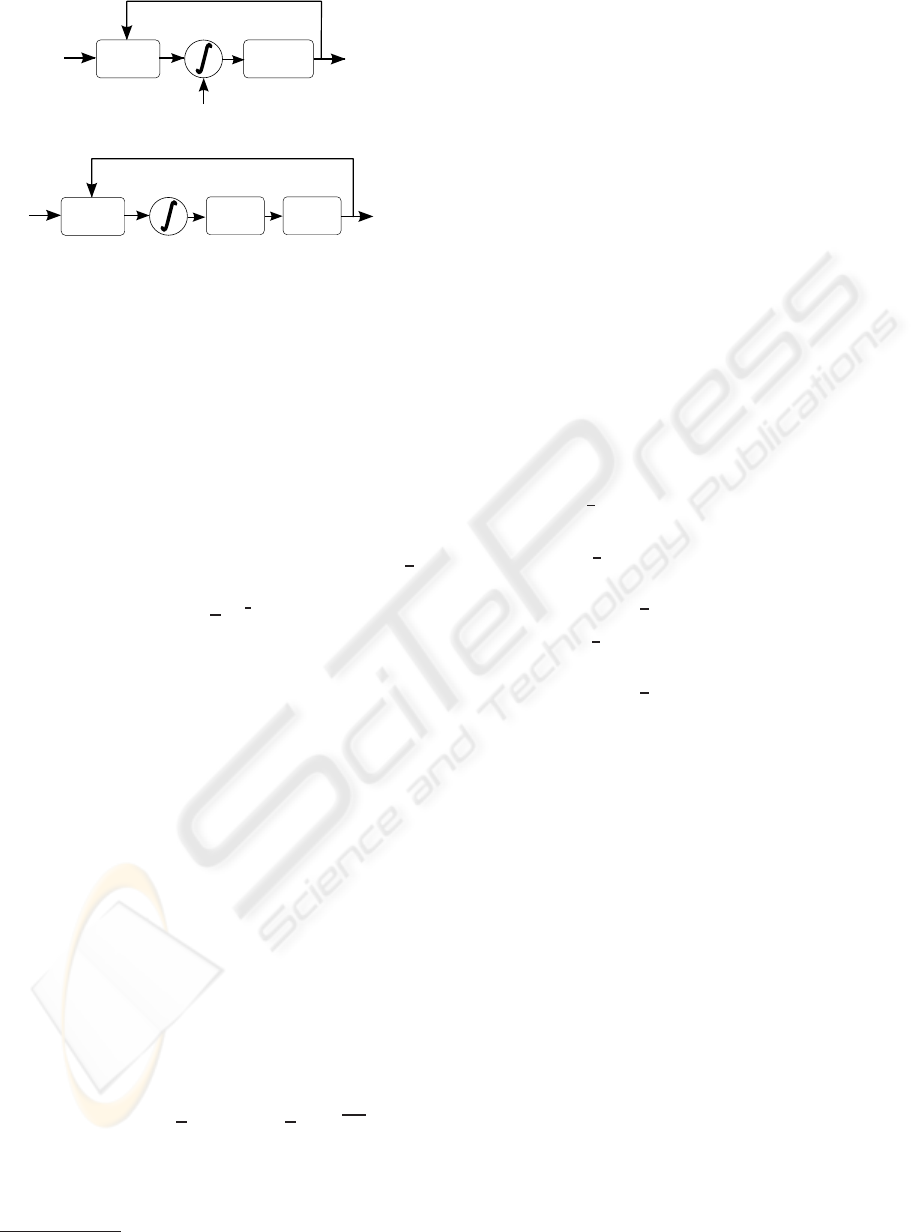
Black-box

G(s,y)

Threshold

block

Visual

Stimuli

Spike

Sequence

v(t)

y(t)

s(t)

i(t)

W(t)

(a) General Stochastic Integrate and Fire model.

Black-box

G(s,y)

Sigmoid

Visual

Stimuli

Spike

Sequence

v(t)

y(t)

s(t)

i(t)

Poisson

Process

(b) Generalised Poisson model.

Figure 1: Changing the noise source in Integrate and Fire

models.

milliseconds, the neuron is reset to a state where the

subthreshold potential is v

. Considering that the last

spike was ﬁred at time t = t

, the solution to (1) is

v(t) =h

(t − t

) ∗

i(t) + v

δ(t −t

) +W(t)

(2a)

W(t) ∼N(0, σ

) , σ

≡ σ(t) (2b)

where ∗ is the convolution operator and h

(t) is the

transfer function of a low pass ﬁlter with a pole in

(t) =

−

H(t) (3)

where H(t) is the Heaviside step function.

2.1 Equivalence between the Slif Model

and the Poisson Based Model

Let us consider a SLIF model as shown in Figure 1(a),

where s(t) represents the visual stimulus, y(t) is the

spike response, and G(s, y) is an arbitrary function

that transforms the pair {stimulus, spike response se-

quence} into the SLIF input i(t). The integrator block

in the ﬁgure represents the linear ﬁlter h

(t).

Under the SLIF model assumption, the noise

source can be moved to the integrator output by modi-

fying its statistics: v(t) = u(t) +W

′

(t) ∼ N(u(t), σ

Considering that after the refrationary period the sub-

threshold potential v follows a Gaussian distribution

with standard deviation σ

, and noting that the con-

volution is a linear operator, the output noise source

remains Gaussian, with standard deviation:

= H(t − t

)



− σ



−2

t−t

(4)

where t

represents the time instant of the last spike

and σ is the standard deviation of the noise during the

integration period, i.e. the Interspike Interval (ISI).

Notice that (1) is similar to the Langevin’s SDE.

Therefore, the probability for eliciting a spike at a

given time instant t is given by the probability for the

potential v(t) = u(t) +W

′

(t) to surpass V



y(t) = 1



= P



u(t) +W

′

(t) ≥ V



= P



′

(t) ≥ V

− u(t)



= 1− N

cdf

− u(t)|0, σ

) =

= N

cdf

(u(t)|V

, σ

) (5)

where N

cdf

(x|µ, σ

) is the normal cumulative distribu-

tion function with mean µ and variance σ

, evaluated

at point x. The function N

cdf

deﬁnes a sigmoid where

controls the translation (centre of the sigmoid) and

controls the expansion of the sigmoid.

Since the spiking probability of the SLIF model

is given by a sigmoid function, the model in Fig-

ure 1(a) is equivalent to the Poisson based model in

Figure 1(b), where the shape of the sigmoid depends

on the noise statistic during the refractionary and in-

tegration periods; three cases can be considered:

(1) if σ

= σ

, the noise variance throughout the in-

tegration period is always the same;

(2) if σ

< σ

, the noise variance increases expo-

nentially from σ

, just after the refractory period,

converging to σ

;

(3) if σ

> σ

, the noise variance decreases expo-

nentially from σ

, just after the refractory period,

converging to σ

;

Equivalently, for a neuron described by the Pois-

son spike generation process presented in Figure 1(b),

the change in noise variance is translated into a vary-

ing slope of the sigmoid – except in case (1). In case

(2)/(3), the model variability increases/decreases as

time from last spike progresses.

However it is worth to notice that this is not a true

Poisson model, as the ﬁring of a spike at a time in-

stant depends on the recent spiking history. Since the

integrator is reset whenever a new spike is ﬁred, this

is true even without the feedback path.

The above conversion thus shows that integrate-

and-ﬁre (IF) models improve the precision of neu-

ron models by adding three important functions to the

typical Poisson based model: i) a natural refractionary

period given by the time for the integrator to recharge

and ﬁre a second spike; ii) a feedback mechanism;

and iii) a sigmoid-like nonlinearity. While the feed-

back mechanism is not absolutely required to achieve

a reasonable precision – see (Capela et al., 2007) –,

the modelling of the feedback mechanism with a suf-

ﬁciently variable ﬁlter allows for a considerable im-

provement on the precision of the model – see (Tom´as

and Sousa, 2007).

TOWARDS A UNIFIED MODEL FOR THE RETINA - Static vs Dynamic Integrate and Fire Models

529

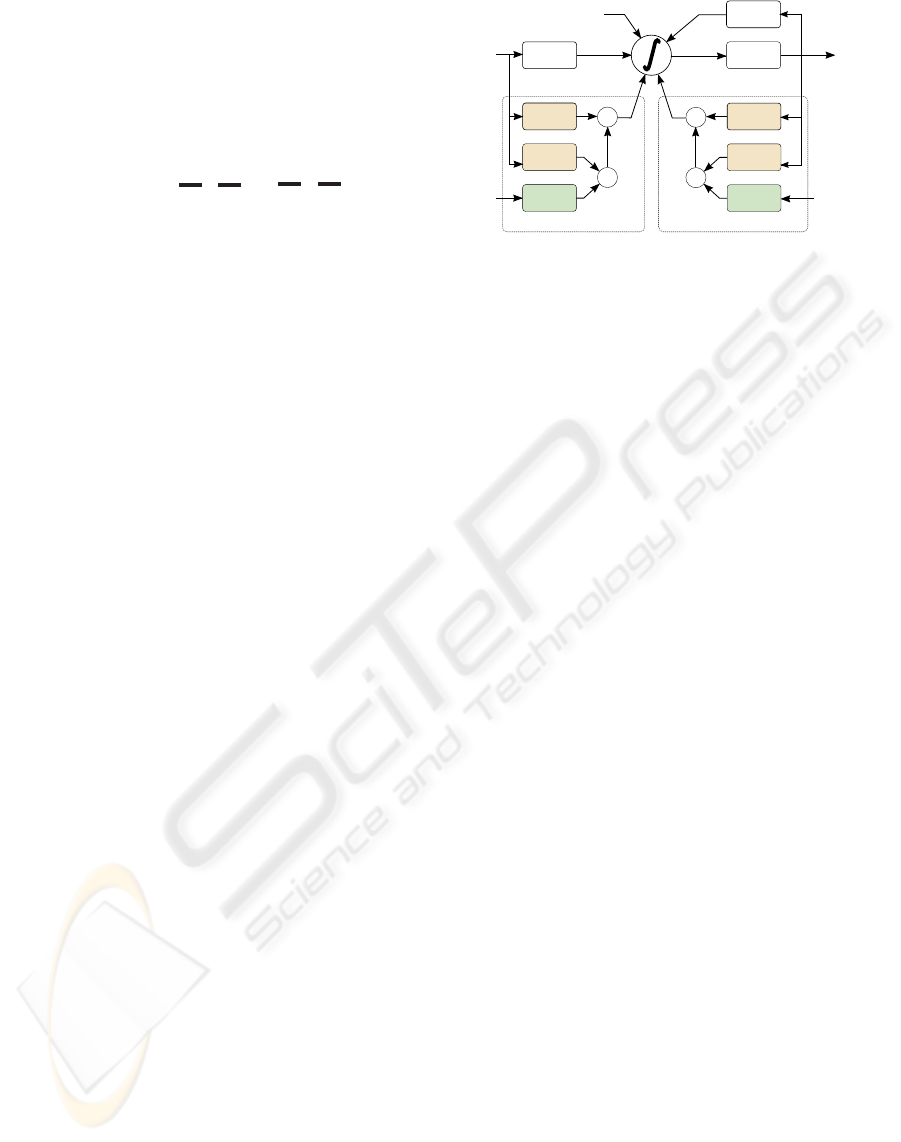
3 DYNAMIC MODEL

The typical modelling of neurons represents G(s, y)

in Figure 1 by a linear system dependent on the input

stimuli s(t) and on spike history y(t):

G(s(t), y(t)) = (h

∗ s)(t)

| {z }

(t)

+(h

∗ y)(t)

| {z }

(t)

(6)

where h

(t) and h

(t) represent the feedforward and

feedback linear ﬁlters, respectively.

In some cases, driven by the necessity to model

the contrast adaptation mechanisms existent in the

retina, non-linear functions are included in the de-

scription of G(s,y) (Baccus and Meister, 2002).

These non-linearities can be, for instance, approxi-

mated by a Taylor series:

G(s(t), y(t)) = f

(t)) + f

(t)) (7a)

(y) =

∑

(7b)

Nevertheless, the inclusion of dynamics in neuron

model is usually avoided, eventhough recent research

suggest that they are required for effectively mod-

elling the precise timing of neurons (Gerstner et al.,

2006). This is particularly veriﬁed in IF neuron mod-

els where its natural non-linearities introduce local

minimums, making the training process harder. In or-

der to model the temporal dynamics of the retina cir-

cuitry, a model must be constructed where the trans-

fer function changes with time, for instance by means

of a modulation process. Typically, neural dynamics

are considered only as a function of the stimuli – e.g.

motion detection (Bialek and van Steveninck, 2005).

However, as referred in section 2, if the precision of

neuron models is improved by the inclusion of a feed-

back path, one should also consider the spike history

for modelling neural dynamics.

The proposed model is divided into two parts: a

static part and a dynamic part. Both parts have depen-

dencies on the stimuli and the spike history. The static

part is composed by a static forward ﬁlter h

(t) and

a static backward ﬁlter h

(t):

(t) = (h

∗ s)(t) (8a)

(t) = (h

∗ y)(t) (8b)

The dynamic part is composed by a set of dynamic

forward linear ﬁlters h

(k)

d f

(t) and dynamic backward

linear ﬁlters h

(k)

(t), whose amplitude is dynamically

controlled by linear functions dependent of both the

Threshold

v(t)

Visual

stimuli

Feedforward dynamic block 'k'

h (t)

fdf

h (t)

fdb

h (t)

bdb

h (t)

bdf

Spike

Sequence

s(t) y(t)

y(t)

s(t)

i (t)

Feedback dynamic block 'k'

W(t)

Figure 2: Dynamic model.

stimulus and the spike history:

(k)

d f

(t) = c

(k)

d f

(t)(h

(k)

d f

∗ s)(t) (9a)

(k)

(t) = c

(k)

(t)(h

(k)

∗ y)(t) (9b)

(k)

d f

(t) =

(k)

fd f

∗ s)(t)+ (h

(k)

fdb

∗ y)(t)

(9c)

(k)

(t) =

(k)

bd f

∗ s)(t)+ (h

(k)

bdb

∗ y)(t)

(9d)

where h

(k)

(t) represents the linear ﬁlter x for compo-

nent k and i

(k)

d f

(t) and i

(k)

(t) are the outputs of the dy-

namic component k. The complete model is depicted

in Figure 2.

The outputs of both the static and the dynamic

components are then added in the integrator block:

i(t) =i

(t) + i

(t) +

∑

(k)

d f

(t) +

∑

(k)

(t) (10)

and the subthreshold potential, v(t), follows (2).

3.1 Model Implementation

To implement the model and estimate its parameters,

it was discretised in time steps of T

= 1 ms, leading

to a discrete representation x

≡ x[n] of the continuous

signal x(t). Basis functions were used for describing

each of the ﬁlters in the model. While one can sim-

ply estimate the value of the ﬁlter for each sample

, the use of basis functions allows: i) to reduce

the dimensionality of the problem, thus accelerating

convergence; and ii) to decrease overﬁtting of the pa-

rameters to the data used during the training step.

Each of the ﬁlters in the static component

(t), x ∈ {sf, sb}, or in its discretised form,



[1], ··· , h

[M]



, where M is the ﬁlter mem-

ory, is deﬁned by means of the basis functions

B = [B

, ··· , B

]

, B

= [b

, ··· , b

] as:

∑

m=1

= A

B (11)

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

530

where A

= [a

, ··· , a

]

. In the case of the ﬁl-

ters in the dynamic components, h

(1)

(t), · ·· , h

(C)

(t),

x ∈ {d f, db, fd f, fdb,bd f, bdb}, one can organ-

ise them in a matrix H



(1)T

, ··· , h

(C)T



(k)



(k)

[1], ··· , h

(k)

[M]



, where the ﬁlters are or-

ganised in rows and the samples in columns. The ﬁl-

tering matrix H

can be computed as:

= A

B (12)

For implementing the integrator linear ﬁlter, an in-

ﬁnite impulse response (IIR) description is used:

(z) =

1− β

1− βz

−1

(13)

where β deﬁnes a pole in s

pole

logβ and log(x) is

the natural logarithm of x. For the system to remain

stable, β ∈ ℜ

]0,1[

, such that s

pole

< 0.

Notice that unlike in the continuous version of the

model, the ﬁlter is now normalised with unitary DC

gain. Thus, the variance of the noise, σ

, at instant n,

given that the last spike event was ﬁred at instant n

becomes:

= β

2(n−n

)

+ (1 − β)

n−n

−1

∑

k=0

= β

2(n−n

)

+ (1 − β)

1− β

2(n−n

)

1− β

(14)

3.2 Model Tuning

The complete set of parameters for the dynamic

model in Figure 2 is:

, A

d f

, A

fd f

, A

fdb

, A

bd f

, A

bdb

β, σ, σ

(15)

However, some parameters depend on others.

Namely, V

and V

depend on the general gains of the

model, A

. Changing their values implies changing

the ﬁlter gains such that the total integration time for

ﬁring a spike remains the same. Also, modifying the

value of β is similar to changing the shape of the other

linear ﬁlters. Moreover, from our experience the ini-

tial noise variance σ

(the variance of the noise after

the refractionary period) does not signiﬁcatively in-

ﬂuence the model tuning. Thus this parameter was re-

moved from the learnable parameter set as well. The

complete set of trainable parameters is therefore:

, A

d f

, A

fd f

, A

fdb

, A

bd f

, A

bdb

, σ

(16)

which corresponds to the basis functions coefﬁcients

for each ﬁlter and the noise standard deviation. The

non-trainable parameters were set to: β = 0.9, σ

= 0,

= 1 and V

= 0.

For the optimisation of the model parameters, a

Bayesian approach was applied to compute the proba-

bility of the spike sequence (Tom´as and Sousa, 2007).

Afterwards, gradient ascent was applied to maximise

this probability. Following (15) from (Tom´as and

Sousa, 2007), the non null gradients in order to the

parameters in (16) are:

= s

∗ B ∗ h

(17a)

= y

n−1

∗ B ∗ h

(17b)

d f



∗ B)(c

d f

)



∗ h

(17c)



n−1

∗ B)(c

)



∗ h

(17d)

fd f



∗ B)(s

∗ A

d f



∗ h

(17e)

fdb



n−1

∗ B)(s

∗ A

d f



∗ h

(17f)

bd f



∗ B)(s

∗ A

d f



∗ h

(17g)

bdb



n−1

∗ B)(y

n−1

∗ A

d f



∗ h

(17h)

dσ

= 2(1− β)

1− β

2(n−n

)

1− β

σ (17i)

where (c

)

= [c

(1)

[n], ··· , c

(C)

[n]]

; the convolution,

represented by the symbol ∗, operates along the

columns of the operands; and the convolution with

is performed using the IIR ﬁlter in (13), resetting

the integration output to V

whenever a spike is ﬁred.

However, unlike in static models, such as those

described in (Tom´as and Sousa, 2007), carefull ini-

tialisation is required in dynamic models. A method

for doing this is to apply spike triggered analy-

sis (Schwartz et al., 2002; Simoncelli et al., 2004).

Eventhough this algorithm is valid under true Pois-

son neuron model, under IF models it becomes bi-

ased (Pillow and Simoncelli, 2003). This is mostly

due to the IF natural non-linearities. However, since

the estimation process of IF models has local mini-

mums, it provides a good starting point.

Since the model includes feedforward and feed-

back dynamic mechanisms, Spike Triggered Average

(STA) and Spike Triggered Covariance (STC) anal-

ysis were performed using both the stimuli and the

spike history. The static ﬁlters h

and h

in Figure 2

were initially set with the shape of the feedforward

and feedback STA, respectively. To adjust the initial

TOWARDS A UNIFIED MODEL FOR THE RETINA - Static vs Dynamic Integrate and Fire Models

531

15 20 25 30

Time [s]

Real

Data

Dynamic

Model

Static

Model

Figure 3: Spike response of the dynamic and static model

vs. the response of real data (vertical lines represent the

timing of the elicited spikes).

shape of the dynamic ﬁlters h

(k)

d f

and h

(k)

, excitatory

and inhibitory directions can be extracted using STC

analysis.

4 EXPERIMENTAL RESULTS

The proposed training algorithm was implemented

and tested to estimate the responses of real rabbit

retina ganglion cells. The data set consists of four

trials of full ﬁeld white noise stimulus, where each

trial has a duration of ≈ 50s with an average count of

6.58 spikes per second. While the stimuli values for

these four trials is the same, small differences exist in

the stimulation time: on average stimulation changed

with a new random value at every 152 ms; the stan-

dard deviation of stimuli change was 238 ms. The

visual stimuli was normalised by subtracting its mean

value and then by dividingit by the standard deviation

of itself. The resulting stimuli, which corresponds to

the inputs

given to the model, is therefore a sequence

of normally distributed random values with zero mean

and unitary standard deviation.

To estimate the dynamic model, many basis func-

tions can be used to describe the linear ﬁlters. Typi-

cal examples are the Laguerre bases (Akc¸ay and Nin-

ness, 1999; Tom´as and Sousa, 2007) or sinusoidal ba-

sis (Keat et al., 2001). However, they are typically un-

able to describe delayed ﬁlters well and, for the used

data, it considerably deteriorated the results. Thus, in

the present work simple Gaussian kernels were used.

While these bases are not orthogonal, they allow to

signiﬁcatively reduce the number of trainable param-

eters, whilst allowing to achieve good results. A total

of 31 kernels were employed each separated by 10 ms,

and having a standard deviation of 5.6 ms.

As depicted in subsection 3.2, for model tuning

Table 1: Error measures between trained models and real

responses.

Spike Inter

NMSE

Time Spike

Static Model

Training mean 420.54 317.69

0.882

trial std 10.39 7.05

All four mean 444.02 337.49

0.903

trials std 12.03 6.95

Dynamic Model

Training mean 251.63 242.62

0.625

trial std 22.13 21.71

All four mean 325.85 281.32

0.808

trials std 20.55 16.68

mean - mean result std - standard deviation

the static ﬁlters h

and h

were initially set with the

shape of the STA applyed to the stimuli and spike his-

tory, respectively. The dynamic ﬁlters h

d f

and h

were set with the 5 most excitatory directions (ex-

tracted by using STC analysis); the experimental data

showed no strong inhibitory directions. The modulat-

ing ﬁlters h

fd f

, h

fdb

, h

bd f

and h

bdb

were initially set

to a small, non-zero value.

To compare the performance of the proposed dy-

namic model, we also performed ﬁtting with a static

model (the number of dynamic blocks in Figure 2 was

set to zero). The training procedure was the same for

both the static and the dynamic model. One of the

ganglion cells’ response trials was used for training.

The other three were used for comparison. Again,

stimulation times are not exactly the same for all tri-

als, which leads to slightly different neuron responses.

For evaluating the performance of the models, 30

spike response trials were produced by using both

the trained static and dynamic models. In Figure 3,

we present the ﬁrst 10 response trials obtained us-

ing the training data set. The ﬁgure also presents the

real retina ganglion cells’ response. Analysing the re-

sponses one can clearly see that the static model is

unable to acquire the structure of the ganglion cells’

response. On the other hand, the dynamic model is

able to accurately reproduce the spike response pat-

tern. However it does tend to ﬁre 15% more spikes

than the ganglion cell (average on the four trials).

For a better assessment of the response of the

models, two error metrics proposed in (Victor and

Purpura, 1997) were used. The ﬁrst metric accounts

for the cost associated with the absolute time of occur-

rence of neuronal events (Spike Time Metric). The

second metric accounts for the cost of changing the

BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing

532

intervals between two spikes (Inter Spike Metric).

The movement cost q was set to 50 s

−1

– see (Vic-

tor and Purpura, 1997). A ﬁring rate metric based on

the normalised mean squared error (NMSE) (Berry II

and Meister, 1998) was also applied. For that purpose,

the ﬁring rates where estimated for both the real and

the estimated data, by convolving their PeriStimulus

Time Histogram (PSTH) (Berry II and Meister, 1998)

with a gaussian window of zero mean and 20ms of

standard deviation.

Cross-evaluation between the models’ responses

and the real ganglion cells responses using the de-

scribed error metrics are presented in Table 1. This

table shows the results when comparing the training

trial and the other trials. The presented error met-

rics conﬁrm our analysis: the dynamic model is able

to capture the dynamics of real retina ganglion cells

which cannot be described by a simple set of a feed-

forward ﬁlter and a feedback ﬁlter. This can be seen

by noticing that the mean values for all error met-

rics are much lower for the dynamic model than for

the static model. The dynamic model also tends to

achieve a higher degree of variability than the static

model. However, this is due to the natural variability

of the real data.

In the presented work, the number of dynamic

components was ﬁxed to ﬁve. However, for obtain-

ing a more general model, one could start by using a

larger number of dynamic components and then us-

ing feature selection – such as in (Tom´as and Sousa,

2007) – to remove all unnecessary components.

5 CONCLUSIONS

Many researchers tend to classify SLIF models and

Poisson-based models into different groups. How-

ever, as show in this paper, the former can be trans-

lated into the latest. One of the most important fea-

tures of the SLIF model is the presence of feed-

back mechanisms. Given that this property helps to

increase the spiking precision, we present a model

whose coefﬁcients are dynamic in time. Moreover we

present a method to estimate its coefﬁcients: it uses

eigen-analysis to estimate the initial parameters and a

gradient ascent technique for tuning the model. Pre-

sented results show that the proposed model is able to

achieve better results than the simpler static models.

REFERENCES

Akc¸ay, H. and Ninness, B. (1999). Orthonormal basis func-

tions for modelling continuous-time systems. Signal

Processing, 77(1):261–274.

Baccus, S. and Meister, M. (2002). Fast and Slow Contrast

Adaptation in Retinal Circuitry. Neuron, 36(5):909–

919.

Berry II, M. J. and Meister, M. (1998). Refractoriness and

neural precision. The Journal of Neuroscience.

Bialek, W. and van Steveninck, R. (2005). Features and

dimensions: Motion estimation in ﬂy vision. Arxiv

preprint q-bio.NC/0505003.

Capela, S., Tom´as, P., and Sousa, L. (2007). Stochas-

tic integrate-and-ﬁre model for the retina. In

15th European Signal Processing Conference (EU-

SIPCO’2007).

Chichilnisky, E. J. (2001). A simple white noise analysis of

neuronal light responses. Network: Computation in

Neural Systems, 12(2):199–213.

Gerstner, W., Jolivet, R., Brette, R., Clopath, C., Rauch, A.,

and Luscher, H. (2006). Predicting Neuronal Activ-

ity with Simple Models of the Threshold Type. Time

(msec), 100:50.

Keat, J., Reinagel, P., Reid, R. C., and Meister, M. (2001).

Predicting every spike: A model for the responses of

visual neurons. Neuron, 30:803–817.

Paninski, L. (2006). The most likely voltage path and

large deviations approximations for integrate-and-ﬁre

neurons. Journal of Computational Neuroscience,

21(1):71–87.

Pillow, J. and Simoncelli, E. (2003). Biases in white noise

analysis due to non-Poisson spike generation. Neuro-

computing, 52(54):109–115.

Schwartz, O., Chichilnisky, E. J., and Simoncelli, E. P.

(2002). Characterizing neural gain control using

spike-triggered covariance. In Dietterich, T. G.,

Becker, S., and Ghahramani, Z., editors, Advances in

Neural Information Processing Systems, volume 14,

pages 269–276, Cambridge, MA. MIT Press.

Simoncelli, E. P., Paninski, L., Pillow, J., and Schwartz, O.

(2004). Characterization of Neural Responses with

Stochastic Stimuli, chapter 23, pages 327–338. MIT

Press.

Tom´as, P. and Sousa, L. (2007). Feature selection for the

stochastic integrate and ﬁre model. In 2007 IEEE In-

ternational Symposium on Intelligent Signal Process-

ing (WISP’2007).

Victor, J. D. and Purpura, K. P. (1997). Metric-space analy-

sis of spike trains: theory, algorithms and application.

Computation Neural Systems, 8:127–164.

TOWARDS A UNIFIED MODEL FOR THE RETINA - Static vs Dynamic Integrate and Fire Models

533