
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION
FOR RESOURCE-CONSTRAINED STREAM PROCESSING
Deepak S. Turaga, Olivier Verscheure, Daby M. Sow and Lisa Amini
IBM T.J. Watson Research Center, 19 Skyline Drive, Hawthorne, NY, USA
Keywords:
Remote Health Monitoring, ECG Compression, Low-complexity, Non-Uniform Sampling, Quantization.
Abstract:
We propose a low-complexity encoding strategy for efficient compression of biomedical signals. At the heart
of our approach is the combination of non-uniform signal sampling together with sample quantization to
improve the source coding efficiency. We propose to jointly extract and quantize information (data samples)
most relevant to the application processing the incoming data in the backend unit. The proposed joint sampling
and quantization method maximizes a user-defined utility metric under system resource constraints such as
maximum transmission rate or encoding computational complexity. We illustrate this optimization problem
on electrocardiogram (ECG) signals, using the Percentage Root-mean-square Difference (PRD) metric as the
utility function measuring the distortion between the original signal and its reconstructed (inverse quantization
and linear interpolation) version. Experiments conducted on the MIT-BIH ECG corpus using the well-accepted
FAN algorithm as the non-uniform sampling method show the effectiveness of our joint strategy: Same PRD
as ’FAN alone’ at half the data rate for less than three times the (low) computational complexity of FAN alone.
1 INTRODUCTION
Remote Health Monitoring is an emerging technol-
ogy allowing medical practitioners to extend their ser-
vices to patients outside of traditional hospital set-
tings. Common remote health monitoring systems are
leveraging pervasive devices such as cellular phones
to collect biomedical readings on patients and relay
the data to servers while being non-intrusive and not
restricting the mobility of patients (Mohomed et al.,
2006). This usage of pervasive devices differ sig-
nificantly from traditional client server usage mod-
els where the pervasive device acts as a client receiv-
ing data from a more powerful server. In the cur-
rent model, the roles are reversed. Pervasive devices
are used to stream data to back-end servers. Their
resource scarceness creates interesting research chal-
lenges dictating the need for efficient, low complex-
ity signal encoding schemes. This work proposes a
generic method for streaming continuous signals un-
der very strict resource constraints while minimizing
the loss in valuable information the original signals
carry.
While our method is applicable to a wide vari-
ety of signals, we describe it in the context of effi-
cient, low complexity compression of electrocardio-
gram (ECG) signals. An ECG signal provides es-
sential information to the cardiologist and is used for
both monitoring and diagnostic purposes. An ECG
monitoring device essentially measures the electrical
impulses that stimulate the heart to contract. Be-
tween 125 and 500 sample points are collected every
second, each coded on 8 or 12 bits (Nygaard et al.,
2001). Thus, a single-lead uncompressed ECG sig-
nal requires between 1 kbps and 6 kbps of sustained
wireless bandwidth. Any application based on wire-
less transmission of even moderate amounts of data
must deal with the reality that usage of wireless spec-
trum will always incur some monetary cost. Efficient,
low complexity compression is thus crucial to make
remote health monitoring via low-end pervasive de-
vices a reality.
The main goal of any compression technique is
to achieve maximum data volume reduction while
preserving the significant signal morphology fea-
tures upon reconstruction (Jalaleddine et al., 1990).
In ECG signal compression algorithms the goal is
to achieve a minimum information rate, while re-
taining the relevant diagnostic information in the
reconstructed signal. Compression techniques for
ECG waveforms can be broadly classified into two
main groups: direct time-domain techniques (Barr,
1988; Cox et al., 1968), and transform-domain tech-
niques (Bradie, 1996; Hilton, 1997; Addison, 2005).
Transform-based methods (e.g., wavelet-based) usu-
ally outperform time-domain techniques but require
96
S. Turaga D., Verscheure O., M. Sow D. and Amini L. (2008).
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION FOR RESOURCE-CONSTRAINED STREAM PROCESSING.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 96-103
DOI: 10.5220/0001067400960103
Copyright
c
SciTePress

a computational power beyond what a mainstream
pervasive device can handle. Instead, well-accepted
time-domain techniques, such as FAN (Barr, 1988)
and AZTEC (Cox et al., 1968), rely on simple heuris-
tics so as to non-uniformly sample the original wave-
form and retain only those data samples that con-
tribute the most to the quality of the reconstructed (in-
terpolated) signal.
Another well-known compression strategy is
quantization. There are two types of quantization.
Vector quantization, where the input symbols are
gathered together in groups called vectors and pro-
cessed to give the output, and scalar quantization,
where each input symbol is treated separately in pro-
ducing the output. Scalar quantization has a low com-
putational complexity, is easy to implement and can
achieve reasonably good compression performance if
applied properly. There has been recent interests in
the scientific community to design schemes perform-
ing jointly both quantization and uniform sampling in
order to match the underlying system resource con-
straints (Derpich et al., 2006). Uniform sampling in-
volves discarding samples of the data regularly to re-
duce the data rate. While uniform sampling can re-
duce the stream rate appropriately it does not guaran-
tee the retention of all samples of interest (features),
especially when the frequency characteristics of the
signal are not well-behaved, which is clearly the case
for ECG waveforms.
This work investigates the benefit of jointly
performing non-uniform sampling (e.g., FAN or
AZTEC) and quantization operations in the context
of remote health monitoring. The paper is organized
as follows: Section 2 introduces some notations and
describes, in generic terms, the concept of joint non-
uniform sampling and quantization. This concept ap-
plied to signal compression is the subject of Section 3,
while Section 4 formulates the problem specifically
for ECG compression under resource constraints us-
ing FAN (Barr, 1988) as the non-uniform sampling
technique. The problem is posed as an optimization
problem. The optimization problem is solved in Sec-
tion 5. Finally, our strategy is validated in Section 6.
And, Section 7 gives concluding remarks.
2 SIGNAL COMPRESSION: NON
UNIFORM SAMPLING AND
QUANTIZATION
Let x[k], 0 ≤ k < N denote a discrete time signal
represented with b
u
bits per sample.
2.1 Non Uniform Sampling
Non uniform sampling of x[k] extracts N
SOI
≤ N sam-
ples of interests (SOI) from x[k]. We denote such
sampling by the operator S : x[k]→x[k
i
] where k
i
cor-
responds to the location of the retained samples of
interest. The operator S is often lossy, and only an
approximation to the original signal x
r
[k] may be re-
covered by interpolating x[k
i
] appropriately. If, af-
ter sampling, we retain N
SOI
out of N samples, the
achieved compression ratio is is
N
SOI
b
u
Nb
u
, correspond-
ing to a rate
N
SOI
b
u
N
bits per sample. Additionally, in
the compressed rate we also need to include the bits
required to encode the locations of the retained sam-
ples, i.e. an additional b
loc
bits per sample. The se-
lectivity of the sampling operator S is controlled by a
sampling sensitivity parameter ε, with low values of
ε corresponding to low selectivity, i.e. most samples
from x[k] are retained. To explicitly indicate the de-
pendence of S on ε, we present it as S
ε
.
2.2 Quantization
Quantization is another well known lossy technique
used to reduce the signal rate, when applications can
tolerate the resultant distortion. We denote the quan-
tization operator as Q : x[k]→ ˆx[k] where ˆx[k] uses
b
q
< b
u
bits per sample, thereby reducing the average
data rate of the stream by a factor
b
u
b
q
.
Given a periodic signal such as ECG, with rela-
tively stationary probability density function (under
known context, i.e. physical activity, health state
etc.) the quantizer sensitivity is controlled only by
the number of desired reconstruction levels
1
L = 2
b
q
.
As before, to explicitly indicate the dependence of Q
on L, we represent it as Q
L
.
2.3 Joint Non-uniform Sampling and
Quantization
Quantization, when used in conjunction with non-
uniform sampling can further reduces the rate of the
stream. When quantization is applied prior to sam-
pling we have the resultant signal S
ε
(Q
L
(x[k])) and
when the signal is sub-sampled before quantization,
the resultant signal is Q
L
(S
ε
(x[k])). Note that these
operators are not commutative, and the two cases are
likely to achieve different compression factors. The
compression gain is multiplicative, i.e. the corre-
sponding rate of signal Q
L
(S
ε
(x[k])) is
N
SOI
b
q
N
+ b
loc
bits per sample.
1
The optimal values of these reconstruction levels are
known for a standard MSE quantizer
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION FOR RESOURCE-CONSTRAINED STREAM
PROCESSING
97

3 DESIGN OF JOINT
NON-UNIFORM SAMPLING
AND QUANTIZATION BASED
COMPRESSION
We can exploit the multiplicative gain in compres-
sion achieved by joint sampling and quantization to
design better signal compression schemes. However,
different types of signals and applications can toler-
ate different levels of quantization noise and require
different numbers of samples of interest. Hence the
joint design of quantization and non-uniform sam-
pling needs to be performed carefully. Consider the
two different operator options S
ε
(Q
L
) and Q
L
(S
ε
),
and let the corresponding rates be
N
S
ε
(Q
L
)
SOI
b
S
ε
(Q
L
)
q
N
+
b
S
ε
(Q
L
)
loc
and
N
Q
L
(S
ε
)
SOI
b
Q
L
(S
ε
)
q
N
+ b
Q
L
(S
ε
)
loc
. In order to de-
sign a good compression scheme, we also need
to formally define a distortion metric. Let x
r
[k]
represent the reconstructed signal, after decompres-
sion, i.e. x
r
[k] = S
−1
ε
(Q
−1
L
(Q
L
(S
ε
(x[k])))) or x
r
[k] =
Q
−1
L
(S
−1
ε
(S
ε
(Q
L
(x[k])))). Then the utility associated
with the compression may be defined in terms of x[k]
and x
r
[k] as U (x[k], x
r
[k]). The goal of designing the
right compression scheme is to maximize this utility
under a rate constraint. If the desired rate constraint
is b
con
(in bits per sample), the optimal compression
scheme may be designed by solving the following
constrained optimizations:
{Q
opt
, S
opt
} = argmax
{Q
L
,S
ε
}
[U (x[k], x
r
[k])]
subject to
N
Q (S
ε
)
SOI
(b
Q
L
(S
ε
)
q
)
N
+ b
Q
L
(S
ε
)
loc
≤b
con
(1)
and
{S
opt
, Q
opt
} = argmax
{S
ε
,Q
L
}
[U (x[k], x
r
[k])]
subject to
N
S
ε
(Q
L
)
SOI
(b
S
ε
(Q
L
)
q
)
N
+ b
S
ε
(Q
L
)
loc
≤b
con
(2)
As mentioned earlier, designing the quantizer Q
L
re-
quires determining the number of quantization lev-
els L and designing the non-uniform sampling S
epsilon
strategy requires determining the optimal value for ε
for a givennon uniform sampling scheme. We thus re-
duce the problem of finding Q
opt
and S
opt
to the iden-
tification of the values of L and ε that maximizes the
utility. Consequently, since b
Q
L
(S
epsilon
)
q
= ⌈log
2
L⌉,1
and 2 can be rewritten as:
{ε
opt
, L
opt
} = argmax
{L,ε}
[U (x[k], x
r
[k])]
subject to
N
Q (S
ε
)
SOI
(⌈log
2
L⌉)
N
+ b
Q
L
(S
ε
)
loc
≤b
con
(3)
and
{ε
opt
, L
opt
} = argmax
{ε,L}
[U (x[k], x
r
[k])]
subject to
N
S
ε
(Q
L
)
SOI
(⌈log
2
L⌉)
N
+ b
S
ε
(Q
L
)
loc
≤r
con
(4)
If the order of the quantization and non-uniform
sampling also needs to be determined, we may com-
pare the optimal utilities in the two cases to deter-
mine the best order. Solving the joint optimization
presented in equations 4 and 3 is non-trivial. This
optimization is heavily dependent on the relationships
between U and N
SOI
and the pair (ε, L). For a generic
sampling algorithm, for a signal with arbitrary char-
acteristics, it is likely to be very difficult to determine
the optimal solution without some form of computa-
tionally complex exhaustive search. In some cases,
however, for sampling algorithms such as FAN, and
for well-behaved signals such as ECG, we show that
these relationships can be estimated experimentally,
and modeled using simple parametric functions. This
enables tractable, and low complexity algorithms to
solve the optimization in real time. In the following
sections, we present several parametric model based
approaches to trade-off computational complexity for
accuracy, while solving this optimization for the FAN
algorithm with MSE quantization for the ECG signal.
4 ENCODING ECG SIGNALS FOR
REMOTE HEALTH
MONITORING
We illustrate our approach to jointly quantize and
sample non uniformly waveforms by focusing on the
representation of electrocardiogram (ECG) signals.
This proposed technique implements adaptive sam-
pling before quantization (i.e. S before Q ).
4.1 Brief Background on ECG Signals
A typical electrocardiogram monitoring device gen-
erates large volumes of digital data. Depending on
the intended application, the sampling rate may range
from 125 to 1000 Hz, with each data sample digitized
to a 8-16 bit value. This translates to a minimum data
rate of 15 KB per minute. Transmitting this signal
over a low-bandwidth channel, especially when ag-
gregating data from multiple sensors, requires com-
pression. The data needs to also be recorded over long
periods, often as much as 24 hours, and doctors may
wish to build a database of ECG recordings for their
patients. Minimizing the storage resources also re-
quires data compression.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
98
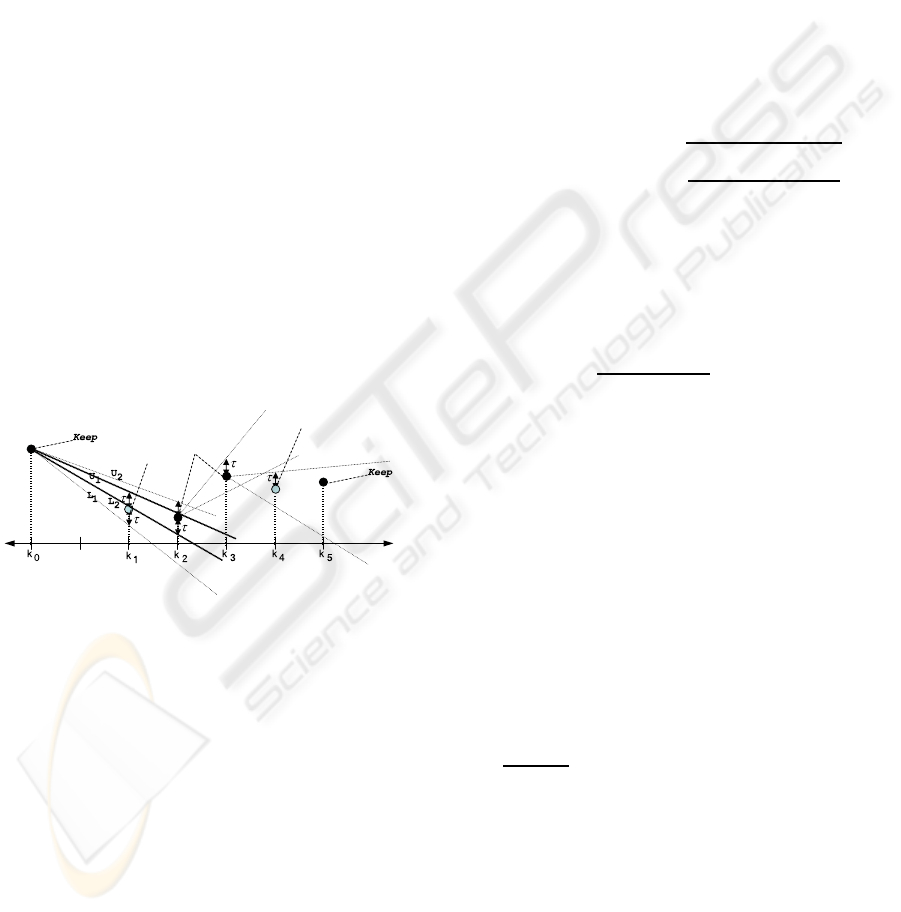
4.2 Adaptive Sampling
FAN (Barr, 1988) is a standard sampling technique
for ECG signal compression and was reported in 1964
by (Gardenhire, 1964). It extracts samples of inter-
est by approximating the signal using a piecewise lin-
ear representation, and discards all but the terminal
points along these line segments. More precisely,
the FAN algorithm replaces the signal with straight
line segments such that none of the original points
lies further from the line segment than some prede-
termined maximum deviation threshold τ. Figure 1
visually describes the algorithm. The first point x[k
0
]
is accepted as non-redundant (permanent sample).
Two slopes {L
1
,U
1
} are drawn between x[k
0
] and
{x[k
1
] − τ, x[k
1
] + τ}. The third sample point x[k
2
)]
falls within the area bounded by the two slopes. Thus
new slopes {L
2
,U
2
} are calculated between x[k
0
] and
x[k
2
] ± τ respectively. Then the two pairs of slopes
are compared and the most restrictive are retained:
U
2
= min(U
2
,U
1
) and L
2
= max(L
1
, L
2
). Since sam-
ple x[k
1
] lies inside the range it is thus discarded;
while x[k
2
] is accepted as a permanent sample and the
procedure above is repeated, comparing future sam-
ple values to the most restrictive lines. During signal
reconstruction, the discarded samples are linearly in-
terpolated from their neighboring retained samples.
Discard
Keep
Discard
Figure 1: FAN algorithm for non-uniform sampling.
The deviation threshold τ determines the quality
of the approximation with large τ leading to more
samples being discarded, and coarser signal approx-
imation. In our setting, this threshold τ maps directly
to the sampling sensitivity ε, and we use the two inter-
changeably. The FAN algorithm has been used widely
for ECG signal compression as it is extremely com-
putationally lightweight (O(N) for N samples), and
performs reasonably well in practice, in terms of re-
taining samples and features of interest. However, for
small target bit-rates (under 2 bits per sample), the
FAN algorithm often underperforms computationally
more complex (O(N
2
)) algorithms such as Cardinal-
ity Constrained Shortest Path (CCSP). In this bit-rate
range, we wish to improve the performance of FAN
by combining it with quantization. Combination with
a simple quantization can retain the low-complexity
nature of FAN, while improving its compression qual-
ity.
4.3 Joint FAN Sampling and
Quantization
The reconstruction quality of compressed ECG sig-
nals is often captured using the percentage root-mean-
square difference (PRD) between the original signal
and its reconstructed (inverse quantization and linear
interpolation) version. The reconstructed signal x
r
[k]
is determined from the sampled and quantized signal
by inverse quantization and linear interpolation.
Hence, the utility function is defined as:
U (x[k], x
r
[k]) = −100∗
v
u
u
t
∑
N
j=1
(x[ j] − x
r
[ j])
2
∑
N
j=1
x[ j]
2
(5)
Finally the joint sampling and quantization prob-
lem, given a rate constraint b
con
(in bits per sample),
may be written as the following optimization:
{ε
opt
, L
opt
} = argmax
{ε,L}
[U (x[k], x
r
[k])]
subject to
N
S
ε
(Q
L
)
SOI
b
S
ε
(Q
L
)
q
N
+ b
S
ε
(Q
L
)
loc
≤b
con
(6)
The search complexity for a naive implementa-
tion of the solution to this problem is O(|Ω
τ
| × |Ω
L
|)
where Ω
ε
is the set of possible values for ε, Ω
L
is
the set of possible values for L and | • | is the car-
dinality operator. This is a constant factor that mul-
tiplies the complexity of the FAN algorithm (thereby
linearly increasing the complexity). However, this is a
worst case metric as it assumes no apriori knowledge
of the underlying ECG signal. Due to the periodic na-
ture of the ECG signal, the designed answer is likely
to change slowly with time (across consecutive win-
dows of N samples each), and hence we can distribute
this complexity over several windows. This may be
done by either solving the optimization once every Z
windows, thereby reducing the overhead complexity
to O(
|Ω
ε
|×|Ω
L
|
Z
) or by reducing the space of possible
search values, i.e. the number of elements in each set
(allowing only for small variations in the previously
designed values).
Additional improvement in performance may be
obtained by actually designing the complete quantizer
(including the design of the optimal resonstruction
levels) dynamically. This however comes at a cost of
increased complexity. In the worst case, a standard k-
means based implementation of quantizer design has
complexity O(N
L
). Of course, this cost may also be
distributed across several windows (due to the nature
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION FOR RESOURCE-CONSTRAINED STREAM
PROCESSING
99
of the ECG signal) to reduce the computational com-
plexity. The design of optimal low-cost quantizers in
conjunction with the sampling is an interesting direc-
tion of future research.
5 MODEL BASED SEARCH
STRATEGY
A model based search strategy is enabled by the rea-
sonably stationary characteristics of the ECG signal,
and the somewhat predictable behavior of the FAN
algorithm. Specifically, we observe, that in a partic-
ular operating region (defined by the rate constraint,
e.g. number of bits per sample, and the correspond-
ing quality metric, i.e. PRD) we may develop simple
parametric models that capture the effect of L and ε
on the utility (PRD) and the rate (bits per sample). As
an example, we run the FAN algorithm several times
on a real ECG signal with different values of ε and
plot the resulting number N
SOI
of samples retained,
and the corresponding distortion PRD in Figure 2.
0 0.05 0.1 0.15 0.2
0
200
400
600
800
1000
1200
ε
N
SOI
0 0.05 0.1 0.15 0.2
0
5
10
15
20
25
30
35
ε
PRD
Figure 2: N
SOI
and PRD as functions of ε.
As is clear, N
SOI
has an almost exponentially de-
caying relationship with ε, while the PRD has a near-
linear relationship with ε, and we can capture these
relationships very simply as follows
N
SOI
(ε) = µe
−νε
(7)
and
PRD(ε) = α+ βε (8)
where µ, ν, α, and β are the model parameters. If we
now combine this sampling with quantization using
L levels, we can derive the resulting bit-rate for the
compressed signal (in bits per sample) as
b
Q
L
(S
ε
)
q
=
N
SOI
log
2
(L)
N
(9)
Using Equation 7, we may rewrite this as
b
Q
L
(S
ε
)
q
=
µe
−νε
log
2
(L)
N
. (10)
In order to build a similar model for the PRD as a joint
function of ε and L, we plot the resulting PRD (after
FAN followed by quantization) in Figure 3. Clearly,
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18 0.2
5
10
15
20
25
30
35
40
45
50
ε
PRD
L=4
L=8
L=16
L=32
L=64
L=128
Figure 3: PRD as function of ε and L.
the slope and intercept of the line relating PRD to ε
change with L. After further investigation, we find
that this relationship may be captured as
α(L) = γe
−ρL
(11)
and
β(L) = η×log(ξL
Q
). (12)
Combining these equations, we may rewrite the
model for PRD after joint sampling followed by quan-
tization as
PRD = γe
−ρL
Q
+ ηεlog(ξL
Q
) (13)
These models for PRD and b
Q
L
(S
ε
)
q
are validated for
a real ECG signal in Figure 4 and Figure 5. While
the models tend to underestimate the real values (es-
pecially for small ε), the shapes of the curves re-
main similar allowing for a search strategy using this
model.
5.1 Three Times FAN Strategy
In order to compress the ECG signal under a rate
constraint, we first partition it into fixed size windows
(each with W samples
2
). Then per window, we run
2
Note that since we process the window independently,
we have N = W
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
100

0
20
40
60
80
0
0.02
0.04
0.06
0.08
0
5
10
15
20
25
30
35
L
ε
PRD
Real
Model
Figure 4: PRD: Real value versus model prediction.
0
20
40
60
80
0
0.02
0.04
0.06
0.08
0
1
2
3
4
5
L
ε
b
q
Q
L
(S
ε
)
Real
Model
Figure 5: b
q
: Real value versus model prediction.
the FAN algorithm for two different values of ε (a
high value and a low value), to determine two values
for N
SOI
followed by quantization with two different
numbers of levels L (a high value and a low value)
to determine four values of PRD. The four values
of PRD provide us with four equations to solve for
parameters γ, ρ, η and ξ. Similarly, the two values
of N
SOI
provide us with two equations to solve for
parameters µ and ν. Once we determine the model
for a given window, it is straightforward to determine
the optimal parameter settings for ε and L under any
specified rate constraint. Once we determine the
optimal parameter settings, we then need to run FAN
once with the selected ε
opt
followed by quantization
with L
opt
levels. Hence, per window we run the FAN
algorithm three times.
5.2 Two Times FAN Strategy
We exploit the near stationarity of the ECG signal
characteristics to reduce the complexity of the Three
Times FAN strategy. Specifically, while for the first
window we employ the same approach (with two
times FAN followed by two times quantization) for
every subsequent window we run the FAN algorithm
for only one additional value of ε followed by quan-
tization with two different values of L. This provides
us with two values of PRD and one value of N
SOI
.
In order to compute the model parameters, we then
combine this with two values of PRD and one value
of N
SOI
computed from the previous window. We al-
ternate between recomputing the PRD and N
SOI
for
the high ε, and the PRD and N
SOI
for the low ε (corre-
spondingly reusing these for the low ε and high ε, re-
spectively, from the previous window), for every suc-
cessive window. Note that it is possible to easily ex-
tend this approach to recompute the model parameters
only once every Z windows, to further reduce com-
plexity. We examine some of the tradeoffs between
complexity and accuracy by comparing the perfor-
mance of these algorithms, and using that to identify
trends for other extensions.
6 EXPERIMENTAL RESULTS
We evaluate the performance of these algorithms on
ECG signals from the MIT-BIH database. Specif-
ically, we use a subset of this database, consisting
of 10 different ECG signals, of duration 8000 sam-
ples each. For these signals we evaluate the different
strategies described in Table 1. We compare FANEX,
FANQEX, FANQMS-3 and FANQMS-2 in terms of
their distortion (PRD)-rate (bits per sample) curves,
and also in terms of their computational complex-
ity. We present results for different processing win-
dow sizes (W) to identify the general performance
trend variations. Each window consists of W sam-
ples of the signal, and is analyzed and processed in-
dependently by the different algorithms, specifically
in terms of computing the optimal parameters ε and
L, and using the FAN algorithm with these param-
eters. We limit the search space for the exhaustive
search strategies by considering a finite small set of
possible values that ε and L can take. For our experi-
ments we have ε∈{0.002, 0.004, ··· , 0.04, 0.05, 0.06}
and L∈{4, 8, 16, 32, 64}. We first consider a process-
ing window of size W = 1000 samples, and present
the distortion-rate (D-R) curve averaged across these
signals (across the 8 windows per signal) for the four
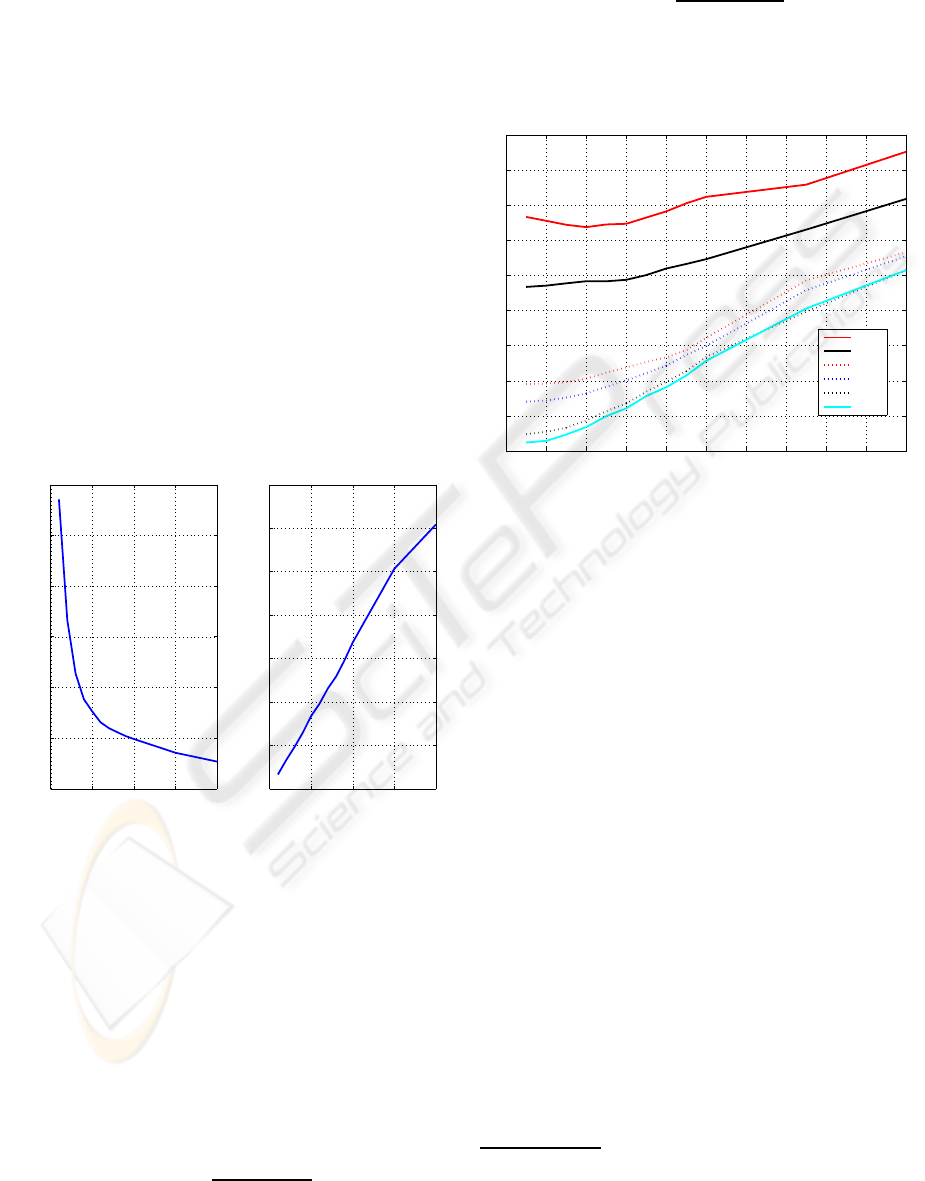
different algorithms in Figure 6.
In Figure 6 we observe that the schemes with joint
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION FOR RESOURCE-CONSTRAINED STREAM
PROCESSING
101
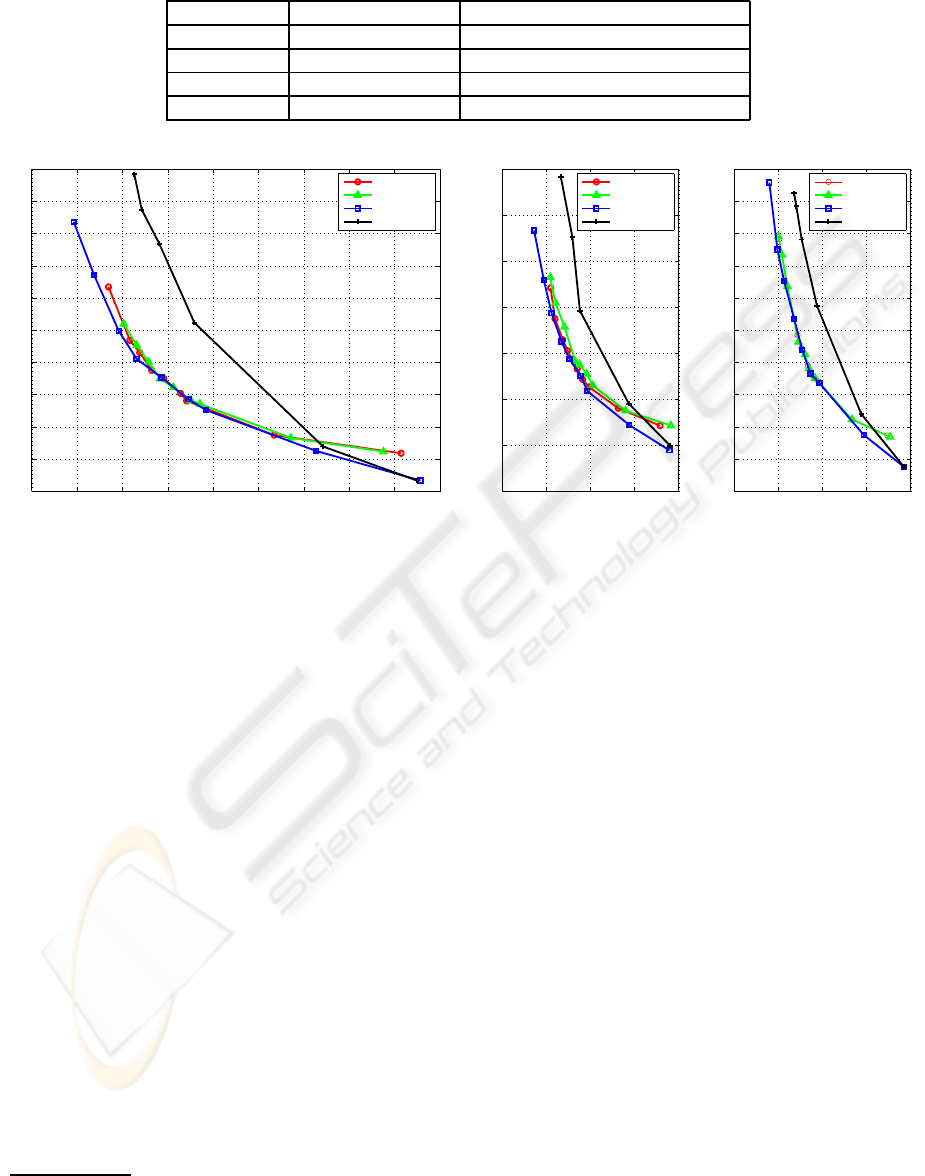
Table 1: Algorithms Considered.
Name Uses Quantization ε only or (ε, L) search strategy
FANEX No Exhaustive
FANQEX Yes Exhaustive
FANQMS-3 Yes Model Based - Three Times FAN
FANQMS-2 Yes Model Based - Two Times FAN
0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
3
4
5
6
7
8
9
10
11
12
13
Bits per sample
Resultant PRD
W=1000 Samples − 8 Windows
FANQMS−3
FANQMS−2
FANQEX
FANEX
Figure 6: D-R Curves: W = 1000.
quantization and FAN significantly outperform the
FAN only scheme, a compression factor of 2 for the
same PRD. This makes the performance of the FAN
algorithm comparable to the state-of-the art compres-
sion algorithms (with significantly higher complex-
ity). Furthermore, we find that the model based
searches FANQMS-3 and FANQMS-2 have perfor-
mance very close to that achieved by the exhaustive
search for target bit-rates less than 2 bits per sample.
As the target bit-rate starts to approach 2 bits per sam-
ple, the model based search strategies underperform
the FANEX strategy, as the models are inaccurate
3
for
this range. However, note that for this higher bit-rate
range, the performance of the FAN algorithm by it-
self is comparable to the best ECG compression algo-
rithms presented, thereby limiting any gains obtained
by additionally quantizing the signal. We also repeat
these experiments for a smaller window (W = 500)
and a larger window (W = 2000, and the results are
presented in Figure 7.
From Figure 7, the same performance trend is ob-
served as in Figure 6 for the four algorithms, how-
ever it is clear that the performance of FANQEX,
FANQMS-2, and FANQMS-3 are closer to each other
for largerW. This may be explained by the fact that a
3
Assumptions on linear, exponential and log-linear rela-
tionships are violated in this range.
0 0.5 1 1.5 2
2
4
6
8
10
12
14
16
Bits per sample
Resultant PRD
W=500 Samples − 16 Windows
FANQMS−3
FANQMS−2
FANQEX
FANEX
0 0.5 1 1.5 2
3
4
5
6
7
8
9
10
11
12
13
Bits per sample
Resultant PRD
W=2000 Samples − 4 Windows
FANQMS−3
FANQMS−2
FANQEX
FANEX
Figure 7: D-R Curves: W = 500(left), W = 2000(right) .
larger window size allows the model based algorithms
to fit better parameterized curves, improving the per-
formance of the model based search schemes. This is
also evident from the fact that on average, the PRD
for the same target bit rate decreases with increasing
W. We also compare the computational complexity of
these algorithms in terms of the amount of CPU time
consumed per window. These CPU times are labeled
t
FANEX
, t
FANQEX
, t
FANQMS−2
and t
FANQMS−3
respec-
tively. We also label the time taken to run the FAN al-
gorithm on one window as t. Instead of presenting ab-
solute numbers, we present relative ratios of the com-
plexity of these algorithms to hide the dependency on
the underlying computer architecture, operating sys-
tem etc. These complexity ratios for the different al-
gorithms are presented in Table 2.
It is evident from Table 2 that FANQMS-3 has 29
(FANQMS-2 has 45 times) lower complexity than
FANQEX and 4 times (FANQMS-2 has 7 times)
lower complexity than FANEX. Further, as expected,
FANQMS-2 has lower complexity than FANQMS-3.
This observation holds across the two different win-
dow sizes considered. Furthermore, FANQMS-3 has
4 times the complexity of FAN, while FANQMS-2
has 3 times the complexity of running FAN one time.
This implies that the search for the optimal ε and L
has the complexity 1.5 times that of the FAN algo-
rithm. Note that by reusing the model parameters
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
102

Table 2: Complexity Comparison.
W
t
FANQEX
t
FANQMS−3
t
FANEX
t
FANQMS−3
t
FANQMS−3
t
t
FANQEX
t
FANQMS−2
t
FANEX
t
FANQMS−2
t
FANQMS−2
t
500 29.18 4.50 4.18 47.75 7.35 2.80
1000 29.06 4.49 4.21 46.07 7.12 2.64
across more windows (updating model infrequently),
this overhead can also be significantly reduced. This
is also indicated by the comparing the rowsof Table 2,
as the complexity gains for FANQMS-2 increase as
W increases from 500 to 1000 (the ratio
t
FANQMS−2
t
de-
creases from 2.80 to 2.64).
7 CONCLUSIONS
We present a low-complexity joint non-uniform sam-
pling and quantization based strategy for signal com-
pression. Specifically, we combine the FAN algo-
rithm with a minimum mean-squared error quantiza-
tion strategy to compress ECG signals. We first for-
mulate the joint design of non-uniform sampling and
quantization for compression, as a constrained opti-
mization problem in terms of maximizing the relevant
distortion metric given the desired compression rate.
The solution of this optimization yields the optimal
sampling sensitivity, and the number of levels to be
used by the quantizer. In general, and for arbitrary
signals, it may not be possible to solve this optimiza-
tion efficiently. However, for ECG signals, we show
that we can develop simple parametric models to cap-
ture the impact of the FAN algorithm and quantiza-
tion on the resulting distortion (PRD) and rate, es-
pecially in very low bit-rate operating regions. Us-
ing these models we can efficiently determine the op-
timal FAN selectivity parameter ε and quantization
levels L to minimize the PRD for a given rate con-
straint. We design two model based algorithms, one
that re-estimates model parameters for every window
(W samples), and another that updates model parame-
ters every alternate window. We show that with these
strategies, we can achieve up to 2 times the compres-
sion rate of FAN (for the same PRD) with a com-
plexity less than 3 times that of FAN alone. We also
show that the performance of these algorithms ap-
proaches (within 10% in rate when ε < 1.8) an ex-
haustive search based strategy for different signals,
and window sizes. Given the low complexity of FAN
our algorithms still remain significantly lower com-
plexity than state-of-the-art transform based compres-
sion schemes, while achieving comparable perfor-
mance. Directions for future research include design
of the optimal search strategy to re-estimate model pa-
rameters (how often, optimal window size etc.), the-
oretical analysis of the signal frequency and statis-
tical properties as well as algorithm complexity for
rate-distortion-complexityoptimal joint sampling and
quantization, and application of these ideas for other
multi-dimensional medical signals.
REFERENCES
Addison, P. S. (2005). Wavelet transforms and the ecg: a
review. In Physiological Measurement, volume 26.
Barr, R. C. (1988). Adaptive sampling of cardiac wave-
forms. In Journal of Electrocardiology, volume 21,
pages 57–60.
Bradie, B. (1996). Wavelet packet-based compression of
single lead ecg. In IEEE Transactions on Biomedical
Engineering, volume 43, pages 493–501.
Cox, J., Fozzard, H., Nolle, F. M., and Oliver, G. (1968).
Aztec: A preprocessing system for real-time ecg
rhythm analysis. In IEEE Transactions on Biomedi-
cal Engineering, volume 15, pages 128–129.
Derpich, M., Quevedo, D., Goodwi, G., and Feue, A.
(2006). Quantization and sampling of not necessar-
ily band-limited signals. In IEEE International Con-
ference on Acoustics, Speech and Signal Processing,
volume 3.
Gardenhire, L. W. (1964). Redundancy reduction the key to
adaptive telemetry. In National Telemetering Confer-
ence, pages 1–16.
Hilton, M. L. (1997). Wavelet and wavelet packet compres-
sion of electrocardiograms. In IEEE Transactions on
Biomedical Engineering, volume 44, pages 394–402.
Jalaleddine, S., Hutchens, C., Strattan, R., and Coberly, W.
(1990). Ecg data compression techniques-a unified
approach. In IEEE Transactions on Biomedical En-
gineering, volume 37, pages 329–343.
Mohomed, I., Ebling, M. R., Jerome, W., and Misra, A.
(2006). Harmoni: Motivation for a health-oriented
adaptive remote monitoring middleware. In Ubi-
Health’06, Fourth International Workshop on Ubiq-
uitous Computing for Pervasive Healthcare Applica-
tions, Irvine, CA, USA.
Nygaard, R., Melnikov, G., and Katsaggelos, A. (2001). A
rate distortion optimal ecg coding algorithm. In IEEE
Transactions on Biomedical Engineering, volume 48,
pages 28–40.
ADAPTATIVE SIGNAL SAMPLING AND SAMPLE QUANTIZATION FOR RESOURCE-CONSTRAINED STREAM
PROCESSING
103
