NON-INVASIVE REAL-TIME FETAL ECG EXTRACTION
A Block-on-Line DSP Implementation based on the JADE Algorithm
Silvia Muceli, Danilo Pani and Luigi Raffo
DIEE - Dept. of Electrical and Electronic Engineering, University of Cagliari, Piazza d’Armi, 09123 Cagliari, Italy
Keywords:
Fetal monitoring, antenatal diagnosis, real-time processing, DSP.
Abstract:
The possibility to access the fetal ECG non-invasively during the early stages of the pregnancy is a paramount
requirement for cardiologists aiming to treat fetuses with congenital hearth diseases. Several research works
have been presented during the past years to address this issue. In this paper we present a block-on-line blind
source separation technique that combines the powerfulness of the batch JADE algorithm to the requirements
of a separation able to adapt to a time-varying mixing process. To avoid estimated sources permutation, a
simple preconditioning technique in conjunction with a proper parameters tuning has been developed and
tested. The whole algorithm has been implemented on a powerful floating-point Digital Signal Processor, and
it is ready to be embedded in an acquisition device for a deeper experimentation.
1 INTRODUCTION
Fetal electrocardiography would allow the early di-
agnosis of some fetal heart congenital diseases, ef-
fectively treatable by transplacental drugs adminis-
tration, that cannot be discovered by means of other
more expensive diagnostic instrumentation such as
ultrasound-based devices. Fetal electrocardiogram
(FECG) extraction from multichannel transabdominal
maternal potential recordingscanbe accomplished re-
sorting to Blind Source Separation (BSS) techniques.
Off-line BSS methods exploiting fourth-order statis-
tics have been proven to be more effective than other
methods but they are very computationally intensive
and unable to deal with long-lasting recordings with
possibly time-varying mixing processes.
In this paper we present a possible solution to such
problems introducing a block-on-line version of the
famous JADE algorithm (Cardoso and Souloumiac,
1993), with the aim to take from it the high separa-
tion quality, at the same time allowing the process-
ing in presence of a potentially time-varying mixing
process. Estimated sources permutation was avoided
by means of a preconditioning technique used in con-
junction with a proper parameter tuning. To assess
the actual real-time capabilities of the algorithm, we
present its porting and simulation on a floating point
Digital Signal Processor (DSP) by Texas Instruments
(TI). Due to such implementation, which still pre-
serves a great portability, the system is ready to be
embedded in an acquisition device for a deeper ex-
perimentation. Separation quality results have been
assessed on a publicly available database.
In Section 2 a short review of some related works
is presented, whereas the proposed algorithm is de-
scribed in Section 3. Section 4 deals with the DSP
implementation of the system. Experimental results
are presented in Section 5. Section 6 concludes this
work.
2 STATE OF THE ART
Non-invasivefetal electrocardiographyis not yet used
in clinical practice because of the difficulty in extract-
ing the signal of interest, particularly in real-time.
Cutaneous recordings from a pregnant woman com-
prise fetal and maternal heart signals, electromyo-
graphic and breathing noises, and external interfer-
ences. Since FECG and maternal ECG (MECG)
have overlapping spectra, they cannot be separated
through conventional frequency selective filtering.
Many methods yield an estimate of the maternal
signal from her chest, then removing this contribu-
tion from the composite abdominal one to obtain
the FECG. Widrow (Widrow and Stearns, 1985) pro-
posed a method of adaptive filtering and noise can-
celling but its performance is very dependent on the
electrodes placement. Camps (Camps et al., 2001)
provided an extension of Widrow’s scheme by includ-
ing in it a finite impulse response neural network. The
drawback is the complexity of the choice of free pa-
458
Muceli S., Pani D. and Raffo L. (2008).
NON-INVASIVE REAL-TIME FETAL ECG EXTRACTION - A Block-on-Line DSP Implementation based on the JADE Algorithm.
In Proceedings of the First International Conference on Bio-inspired Systems and Signal Processing, pages 458-463
DOI: 10.5220/0001066804580463
Copyright
c
 SciTePress

rameters, whose number increases geometrically with
the number of inputs, though without eliminating the
problem of high sensitivity to electrodes placement.
Kanjilal (Kanjilal et al., 1997) used Singular Value
Decomposition (SVD) to recover fetal and maternal
components from a single channel. Since this method
is based on nearly periodicity of ECG signals, it is
unsuitable to detect unexpected patterns. Mochimaru
(Mochimaru et al., 2002) suggested a wavelet-based
method, but this approach suffers in presence of over-
lapping maternal and fetal QRS complexes.
BSS aims to recover the source signals from a
set of mixtures without a priori knowledge of the
mixing process (blindly). Under the hypothesis that
the mixing process is linear, if we denote with s
the n-dimensional vector of sources, with x the m-
dimensional vector of observed mixtures and with
A ∈ R
m×n
the mixing matrix, the problem can be
mathematically formulated as in (1):
x(k) = As(k) (1)
where k represents a discrete time index. The solu-
tion consists in finding an unmixing matrix B ∈ R
n×m
such that
ˆ
s(k) = Bx(k) is a good estimation of s up to
a permutation and a multiplicative constant (the two
BSS ambiguities).
Source separation can be accomplished by Prin-
cipal Component Analysis (PCA) and Independent
Component Analysis (ICA). PCA looks for compo-
nents which are uncorrelated, whereas ICA looks for
components which are statistically independent, i.e.
whose higher order cumulants are all diagonal ten-
sors. Since uncorrelated sources are not necessarily
independent, unless they have a Gaussian distribution,
and ECG signals are known to be super-Gaussian,
ICA is more appropriate than PCA, producing bet-
ter results (Bacharakis et al., 1996). Sources involved
in this application descend from different bioelectric
phenomena and can be fairly considered statistically
independent. It is also well-accepted that MECG
gives rise to 3 source signals and FECG can be rep-
resented by means of 2 source signals (Nandi and
Zarzoso, 1997). Hence it suffices to have a number
of observed mixtures not lower than the number of
sources to ensure the identifiability of ICA model. In
the following, we assume m = n, then all vectors will
be n-dimensional and all matrices will be n× n.
Since De Lathauwer (De Lathauwer, 1995) has
first used ICA to separate FECG successfully, many
researchers resorted to the same approach, proved to
perform better than the Widrow’s method (Zarzoso
and Nandi, 2001), and rather robust with respect to
electrodes placement. De Lathauwer (De Lathauwer
et al., 2000) showed ICA capability to reveal ectopic
beats in a regular ECG, differently from other ap-
proaches making assumptions on the signal charac-
teristics. This property makes BSS by means of ICA
suitable for medical applications.
3 THE PROPOSED ALGORITHM
All the algorithms cited in Section 2 process data in
batch mode, so they can be used only if the mixing
process does not change over time. Since both mother
and fetus can move, the separation algorithm must be
able to track such changes. Some on-line solutions
have been conceived but, unlike batch ones, the qual-
ity of the estimated sources is quite poor. We identi-
fied a good on-line algorithm in terms of separation
quality in Mermaid (Marossero et al., 2003) but the
main drawback is the parameter tuning, since several
parameters have to be chosen empirically to achieve
a good-quality signal. Balancing pros and cons of
both batch and on-line techniques, we chose to de-
rive a block-on-line method from a batch one: JADE
(Cardoso and Souloumiac, 1993).
3.1 Background: The Jade Algorithm
In the JADE algorithm the ICA problem is solved by
means of a two-stage procedure consisting of a pre-
liminary processing performed by employing Second-
Order Statistics (SOS) and a second one performed by
resorting to Higher-Order Statistics (HOS). The first
stage, multiplying by a whitening matrix W the ob-
served mixtures, decorrelates and normalizes them;
the second stage aims to obtain higher-order indepen-
dence by multiplying decorrelated mixtures by an or-
thogonal rotation matrix G which minimizes the sum
of squared fourth order cross cumulants of whitened
observations:
Ψ =
∑
ijkl6=iikl
K
ijkl
2
(2)
The G matrix is found by joint diagonalization
of the cumulant matrices, efficiently performed by
Jacobi method. This technique works by repeated
sweeps of plane rotations, each one applied to a pair
of rows of the cumulant matrices. During a sweep,
for each pair (i, j) with 1 ≤ i ≤ n, the Givens angle
θ
ij
which minimizes the contrast is calculated and if
θ
ij
> θ
th
(θ
th
is a threshold angle whose value deter-
mines the optimization accuracy) the pair is rotated.
The convergence is obtained when no pairs have been
rotated over a sweep. This optimization procedure
does not suffer from problems of convergence, as op-
NON-INVASIVE REAL-TIME FETAL ECG EXTRACTION - A Block-on-Line DSP Implementation based on the JADE
Algorithm
459

posed to the gradient descent algorithm, and does not
show the difficulty of parameters tuning.
The blind identifiability requires the diagonaliza-
tion of the whole fourth-order cumulant set (n
2
cu-
mulant matrices). The original JADE algorithm deals
with complex signals and finds the G matrix by ap-
proximate joint diagonalization of the n most signif-
icant cumulant matrices, to reduce the computational
load. Since we are dealing with real signals, we can
exploit the symmetries of the cumulants to reduce to
n(n+1)/2 the number of matrices to be diagonalized,
without statistical loss (Cardoso, 1999).
3.2 On-Line Jade Implementation
For a batch algorithm, the permutation ambiguity is
simply the obvious outcome of the mathematical for-
mulation of the problem: the order of the sources is
unpredictable and usually insignificant. It comes to be
a critical problem in block-on-line algorithms, where
the estimated sources can be differently ordered in
different blocks, so that channels can swap produc-
ing meaningless signals. We solved this problem by
combining a sliding window strategy (window length:
L samples, overlap: (L− T) samples) with a two-step
HOS stage. First of all, the algorithm performs the
preprocessing stage (SOS, i.e. centering and whiten-
ing) on a sample-by-sample basis. The data stream
is subdivided into data blocks X of length T, with
X = {x(k),0 ≤ k < T}. Recorded data of a block are
centered subtracting their mean value by means of a
running average given by:
x(k) = (1− γ)x(k− 1) + γx(k), (3)
where γ is a forgetting factor. We chose γ = 1/L so
that the memory depth is equal to the sliding window
length. Centered data are whitened as follows:
z(k) = W(k)(x(k) − x(k)) (4)
and whitening matrix is updated using an approach
adapted from (Cardoso and Laheld, 1996):
W(k+ 1) =
= W(k) −
λ
0
1+λ
0
z(k)
T
z(k)
(z(k)z(k)
T
− I)W(k)
(5)
where λ
0
is a constant. The smaller λ
0
the slower
the convergence, but with high values it is easier to
incur in instability. The newest T preprocessed data
are inserted in a L-wide window Z = {z(k),0 ≤ k <
L} with the last L− T preprocessed samples.
After that, in the HOS stage, we precondition the
rotation process by a coarse separation of the actual
block of whitened mixtures with the rotation matrix of
the previous block. This procedure considers that fe-
tal movements can change the physical configuration
and consequently the mixing matrix but, if T is cho-
sen so that two consecutive blocks are close enough
from a temporal point of view with respect to the dy-
namics of the mixing process, the coarse separation
rotates whitened observations so that the basis vec-
tors (the columns of the mixing matrix) of the current
block are close to the basis vectors of the previous
block. Coarse-separated mixtures are then used for
the computation of the cumulant matrices and their
joint diagonalization. At last, the fine separation ma-
trix G is provided in output, the optimization pro-
cess being carried out in the direction started from the
coarse separation. The algorithm can be described by
the following steps:
1. Acquire a block X of T new samples X =
{x(k), 0 ≤ k < T};
2. For all k so that 0 ≤ k < T:
(a) Center x(k) by subtracting x(k) calculated as in
(3), and keep x(T −1) as the x(− 1) for the next
block;
(b) Whiten (x(k) − x(k)) according to (4) to obtain
z(k);
(c) Update the whitening matrix following (5) and
keep W(T − 1) as the W(−1) for the next
block;
(d) Insert z(k) in Z(L− T + k);
3. Perform the coarse separation of Z: Y
′
= Q
prev
Z;
4. Apply JADE algorithm to Y
′
to obtain the matrix
G;
5. Perform the fine separation Y = GY
′
;
6. Update the rotation matrix Q
cur
= GQ
prev
,
Q
prev
= Q
cur
;
7. Go to 1 for another block.
3.3 Parameters Setting
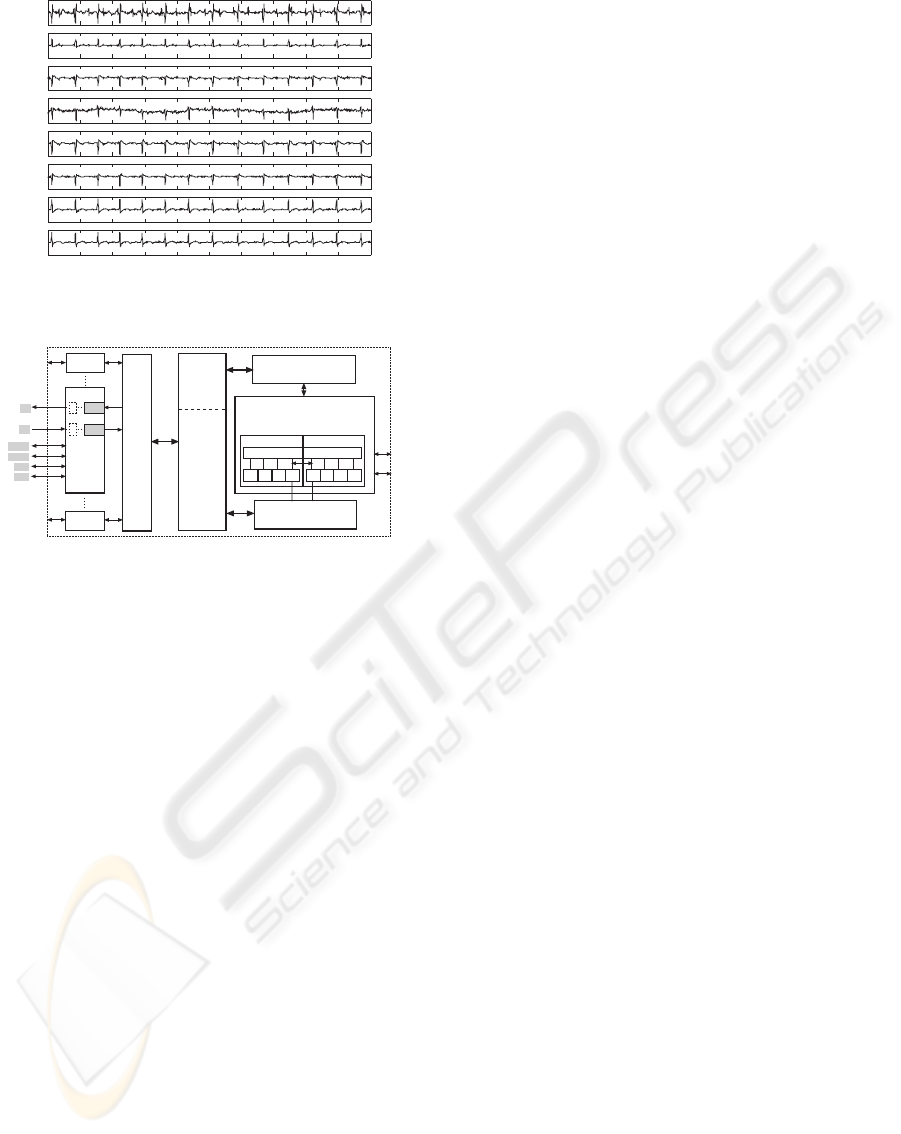
The proposed algorithm has been applied to a real
dataset consisting of n = 8 potential recordings, the
first 5 abdominal and the last 3 thoracic. The dataset
(BIOMED, 2005) is recorded at a sampling rate of
250 Hz, and it is composed of 2500 samples (Fig-
ure 1). It represents the benchmark used in most of
research works about fetal ECG extraction. We set λ
0
to 0.001. The choice of L and T aims at achieving a
good trade-off among permutation rejection, separa-
tion quality and computational efficiency. L and T are
set to be 1024 and 256 respectively. A higher T gives
rise to ECG channels swapping, a higher L increases
the needed floating point operations (FLOPS) without
improving the separation quality.
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
460

-50
0
50
-200
0
200
-100
0
100
-50
0
50
-100
0
100
-1000
0
1000
-1000
0
1000
0 1 2 3 4 5 6 7 8 9 10
-1000
0
1000
Figure 1: The real signal mixtures (BIOMED, 2005).
8-issue VLIW
DSP architecture
C67x CPU
Level1 instruction cache
(4KB)
Level2
cache
up to 4-way,
64KB max
16 ch
EDMA
EMIF
McBSP1
Timer1
L1 D1M1S1 D2 L2S2M2
reg file A reg file B
data path A
data path B
Level1 data cache
2-way (4KB)
Level2
memory
192KB
TMS320C6713 DSP
DXR
DRR
DR
DX
CLKX
CLKR
FSX
FSR
Figure 2: A block diagram of the simulated system.
4 THE DSP SYSTEM DESIGN
Modern electrocardiographs are based on DSPs,
sometimes joined to a microcontroller for the user in-
terface. The main problems of such implementations
are the limited amount of memory available both on
chip and on board and the low operating frequency,
compared to PC processors. Conversely, DSPs are
significantly less power hungry and highly optimized
for signal processing operations. Almost all the de-
vices on the market can be programmed in C or C++,
so enhancing code portability. However, some per-
formance improvements can be achieved only by ex-
ploiting at the most the architectural characteristics of
the processor and then also assembly-written routines.
All these aspects have been carefully taken into ac-
count in the proposed real-time system design.
The algorithm has been coded in C to work by
file I/O on a PC, and then ported on a TMS320C6713
DSP, a TI 1800MFLOPS floating point VLIW proces-
sor up to 300MHz. Having to rely only on recorded
signals, we avoided any hardware board implemen-
tation. To evaluate the real-time capabilities of the
proposed DSP solution, it has been simulated under
Code Composer Studio (CCS) 3.1, the Integrated De-
velopment Environment for the TI processors, with
the Device Cycle Accurate Simulator as target. It is
able to give an indication of the cycle count of the
application with cycle accuracy even at peripherals
level. The target DSP provides a rich set of on-chip
advanced peripherals. Among them, we used one of
the two Multi-channel Buffered Serial Ports (McBSP)
available on chip, and the Enhanced Direct Memory
Access Controller (EDMA).
Data enter the system through the McBSP1 in
frames composed of 8 channels of the ECG, 16
bit/sample, with the proper sampling rate. The
EDMA manages the acquisition performing a data or-
dering in an array placed in the internal L2 memory,
so that at the end of a block acquisition such array is
composed of 8 contiguous blocks of T samples, each
one consisting only of the input samples for one chan-
nel. At the same time, the output samples are out-
putted through the same serial port with the inverse re-
ordering procedure. The CCS Port Connect and Pin
Connect features were used to provide the McBSP1
with the external clocks and frame syncs needed to
correctly perform both the sample acquisition and the
outputs collection, thus emulating a real hardware
system. A simplified representation of the simulated
system is depicted in Figure 2, where the externally
driven pins (CLKX, CLKR, FSX, FSR) and ports
(DXR and DRR) are shadowed. To guarantee stable
input signals during the acquisition of a next block,
EDMA performs automatic ping-pong buffering. The
newest T samples X
i
are acquired during the process-
ing of the previous block Z
i−1
, so that the overall pro-
cessing time must be less than T
X
= T/ f
s
. This way
the interrupt signal period is also equal to T
X
. Af-
ter sample-by-sample pre-processing, a Quick DMA
(QDMA) call performs the sliding window mecha-
nism needed for the HOS stage. We used fastRTS
and DSPlib for highly optimized math functions and
DSP array operations respectively. The access to the
external memory dramatically increases the latency,
whilst the wide data arrays substantially reduce the
code space. With the chosen target, which comes with
256KB L2 internal RAM, and several optimizations,
no external memory is required.
5 EXPERIMENTAL RESULTS
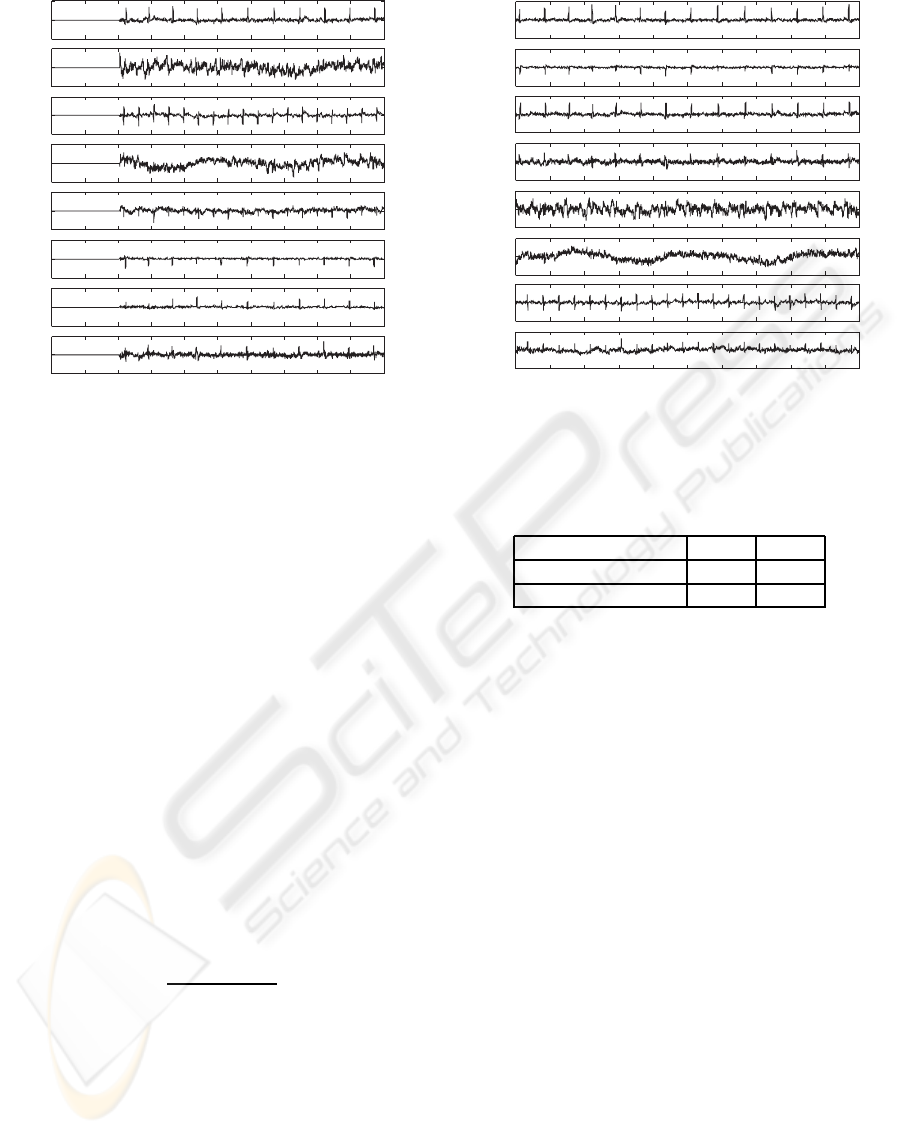
The sources estimated by means of the on-line algo-
rithm are depicted in Figure 3. ECG channels do not
suffer from the permutation problem, whereas there is
a suspect permutation in the y
2
and y
4
noise channels.
Such different robustness to permutations can be ex-
plained in the light of fact that cumulant based meth-
ods need a large number of samples to reach good
separation results. The L value has been chosen so
NON-INVASIVE REAL-TIME FETAL ECG EXTRACTION - A Block-on-Line DSP Implementation based on the JADE
Algorithm
461

-10
0
10
y
1
-5
0
5
y
2
-10
0
10
y
3
-5
0
5
y
4
-10
0
10
y
5
-20
0
20
y
6
-20
0
20
y
7
0 1 2 3 4 5 6 7 8 9 10
-10
0
10
y
8
time [s]
Figure 3: The sources estimated with the proposed on-line
solution. The blanked parts of the signals at the beginning
are due to the initialization of the on-line whitening proce-
dure. Traces y
3
and y
5
clearly show the FECG, the hearth
rate being almost twice the maternal one.
that a window contains some periods of ECG signals.
Such noises can be interpreted as maternal respiration
and electromyogram. Since respiration baseline wan-
der is characterized by a pseudo-period higher than
the one of ECG, we should work with a wider win-
dow to make up to a window containing some peri-
ods of fluctuation due to the maternal respiration, but
this would increment the computational load. Fur-
thermore some more unstructured noises could take
no advantageof such resizing. Since our target are the
ECG signals, we can disregard noise channels, main-
taining L = 1024. With this choice, ECG waveforms
are reconstructed with the same quality of the origi-
nal JADE algorithm (Figure 4). To compare the per-
formance of the two methods, we used the parameter
proposed in (Bacharakis et al., 1996):
P
K
=
|K
40
| + |K
04
|
∑
m+n=4
|K
mn
|
(6)
P
K
represents the ratio between the sum of the mod-
ulus of the fourth-order auto-cumulants of two esti-
mated sources and the sum of the modulus of all the
fourth-order cumulants related to the same sources.
If two components are really independent their cross-
cumulants are close to 0, then the ratio tends to 1. In
Table 1 are reported the cumulative results for all the
signal couples, in terms of average value and stan-
dard deviation. It proves that the two methods allow
to reach very similar source independence.
-10
0
10
Y
1
-20
0
20
Y
2
-10
0
10
Y
3
-10
0
10
Y
4
-5
0
5
Y
5
-5
0
5
Y
6
-10
0
10
Y
7
0 1 2 3 4 5 6 7 8 9 10
-10
0
10
time [s]
Y
8
Figure 4: The sources estimated with the batch JADE algo-
rithm. Traces Y
7
and Y
8
clearly show the FECG.
Table 1: Original batch JADE vs. block-on-line JADE. Av-
erage and standard deviation of the parameter P
K
.
avg STD
Batch Algorithm 0.918 0.066
On-line Algorithm 0.912 0.109
5.1 Profiling Results
Performance have been also evaluated by means of
cycle profiling to assess the real-time constraints sat-
isfaction. From Table 2 we can see that the system
largely respects the real-time requirements, since T
X
is almost equal to 1 second and the DSP is running
at 300 MHz. Hence, it will be possible either to add
further pre/post processing to the actual implementa-
tion (such as signal enhancement, fetal QRS detec-
tion, fetal ECG delineation and measurement) and to
safely reduce the clock rate. From Table 2 it is pos-
sible to notice that the time spent for the execution of
the algorithm with the number of sweeps required (on
the same block Z
i
), T
tot
, represents about 8.3% of T
X
,
pre-processing requires less than 7% of T
tot
, and the
coarse separation plus Q
prev
update less than 0.9% of
T
tot
. On the available records, we counted a maximum
of 6 sweeps. In the HOS stage cycle count, there is a
considerable offset due to the cumulant matrices com-
putation that can be quantified in 21,399,260 clock
cycles, 83.8% of T
tot
. It can be estimated that every
pairwise Givensrotation requires 13,534 clock cycles,
0.05% of T
tot
. Hence, considering that 1 sweep, in the
worst case, consists of maximum 28 Givens rotations,
and that the coarse-separation dramatically reduces
BIOSIGNALS 2008 - International Conference on Bio-inspired Systems and Signal Processing
462

Table 2: Profiling results for the DSP implementation: (a).
for the whole algorithm on a single block allowing all the
required sweeps, and (b) for only the 2
nd
step of the HOS
stage allowing a different (imposed) number of sweeps.
Algorithm section # ck ticks
Pre-processing 1,714,300
(a) Coarse-sep. + Q
prev
update 220,258
step of the HOS stage 23,599,929
1 sweep 21,557,940
(b) 2 sweep 21,936,878
6 sweeps (threshold control) 23,599,929
the need for many sweeps, the number of sweeps is
not a performance limiter.
6 CONCLUSIONS
In this paper a block on-line version of the JADE al-
gorithm and its real time implementation on a floating
point DSP has been presented and evaluated in terms
of both separation quality and profiling. Separation
quality results are in line with those achievable with
the batch JADE algorithm. This can be interpreted in
the light of the considerations presented in Section 5
since the signal is extremely clear and stable so that
it is possible to assume that mixing process does not
changes a lot over time. At the same time, longer sig-
nals will benefit from the block-on-line implementa-
tion with preconditioningsince the probability to have
a stable mixing process over the whole recording is
very low. The DSP implementation proved the possi-
bility to use this algorithm in real-time on a portable
device. The system is powerful enough to use only
less than 10% of the overall available processing time
to execute the algorithm, then leaving space for fur-
ther processing actually required in a real implemen-
tation. The realization of a front-end analog circuitry
for signals acquisition will enable the trial with cus-
tom databases.
ACKNOWLEDGEMENTS
The authors wish to thank Dr. R. Tumbarello (MD.
Head, Division of Pediatric Cardiology) and Dr. S.
Mura (Division of Gynecology and Obstetrics) of the
Hospital “G. Brotzu”, Cagliari, Italy.
REFERENCES
Bacharakis, E., Nandi, A. K., and Zarzoso, V. (1996). Foetal
ECG extraction using Blind Source Separation meth-
ods. In Proc. EUSIPCO96, pages 395–398.
BIOMED (2005). Katholieke Universiteit Leu-
ven, Belgium, http://homes.esat.kuleuven.be/
∼biomed/biosource/data006/foetal ecg.dat.
Camps, G., Martinez, M., and Soria, E. (2001). Fetal ECG
Extraction using an FIR Neural Network. Computers
in Cardiology, pages 23–26.
Cardoso, J. and Souloumiac, A. (1993). Blind beamforming
for non-Gaussian signals. In IEEE PROCEEDINGSF,
volume 140, pages 362–370.
Cardoso, J. F. (1999). High-order contrasts for independent
component analysis. Neural Computation, 11(1):157–
192.
Cardoso, J. F. and Laheld, B. (1996). Equivariant adaptive
source separation. IEEE Trans. on S.P., 44(12):3017–
3030.
De Lathauwer, L. (1995). Fetal Electrocardiogram Extrac-
tion by Source Subspace Separation. In Proc. IEEE
Workshop on HOS, pages 134–138, Girona (Spain).
De Lathauwer, L., Moor, B. D., and Vandewalle, J. (2000).
Fetal Electrocardiogram Extraction by Blind Source
Subspace Separation. IEEE Trans. on Biomedical En-
gineering, 47(5):567–572.
Kanjilal, P. P., Palit, S., and Saha, G. (1997). Fetal ECG
extraction from single-channel maternal ECG using
singular value decomposition. IEEE Transactions on
Biomedical Engineering, 44(1):51–59.
Marossero, D., Erdogmus, D., Euliano, N., Principe, J., and
Hild, K. E. (2003). Independent component analysis
for fetal electrocardiogram extraction: a case for the
data efficient MERMAID algorithm. pages 399–408.
Mochimaru, F., Fujimoto, Y., and Ishikawa, Y. (2002). De-
tecting the fetal electrocardiogram by wavelet theory-
based methods. Progress in Biomedical Research,
7(3):185–193.
Nandi, A. and Zarzoso, V. (1997). Foetal ECG separation.
In IEE Colloquium on the Use of Model Based Dig-
ital Signal Processing Techniques in the Analysis of
Biomedical Signals (No. 1997/009), pages 8/1–8/6.
Widrow, B. and Stearns, S. D. (1985). Adaptive Signal Pro-
cessing. Prentice-Hall Signal Processing Series.
Zarzoso, V. and Nandi, A. K. (2001). Noninvasive fetal
electrocardiogram extraction: Blind separation versus
adaptive noise cancellation. IEEE Transactions on
biomedical engineering, 48(1).
NON-INVASIVE REAL-TIME FETAL ECG EXTRACTION - A Block-on-Line DSP Implementation based on the JADE
Algorithm
463