AUGMENTED COMANIPULATION IN ROBOTIC SURGERY

B. Cagneau, D. Bellot, G. Morel,

Institut des Syst`emes Intelligents et Robotique, 18 route du Panorama, 92265 Fontenay Aux Roses, France

N. Zemiti

TIMC-IMAG Laboratory, 38706 La Tronche Cedex France

G. D’Agostino

Universit`a Federico II di Napoli, Facolt`a di Ingegneria dell’Automazione, Corso Umberto I, 80138 Napoli, Italy

Keywords:

Force control, robotic surgery, cobotic, augmented comanipulation.

Abstract:

This paper presents a control scheme for augmented comanipulation with force feedback in robotic surgery.

This approach aims at increasing the surgeon’s dexterity. The surgeon manipulates a handle mounted on the

robot which manipulates the instrument. The control law ensures that the instrument applies on the organ

the same forces that the surgeon applies on the handle but decreased by a scale factor. As a consequence,

the robotic device provides the surgeon with an augmented sensation of the interaction forces between the

instrument and the organ. The proposed control law does not require any knowledge of the environment. This

control scheme is proven stable thanks to a passivity study. Indeed, passivity analysis is a useful tool for the

stability analysis of a robot interacting with an unknown environment. Experimental results are presented on

a robot dedicated to minimally invasive surgery.

1 INTRODUCTION

In the context of robotic surgery, the surgeon and the

medical staff have to interact with the robot. Depend-

ing on the surgical task, the degree of cooperation can

be really different. Simple tasks may be realized by

the robot, in an autonomous way, under the surgeon’s

supervision. For example, the surgeon deﬁnes the de-

sired positions via an interface and the robot moves

to these positions. However more complex tasks re-

quire the surgeon’sjudgment and, thus, cannot be per-

formed autonomously by the robot. These tasks re-

quire that the robot works in cooperation with the sur-

geon. The surgeon’s skills are thus improved as the

robot increases his dexterity. To do so, one of the

possibilities is robot’s force control. For instance, in

minimally invasive surgery, a robotic device could be

used in order to display manipulation forces back to

the surgeon. Indeed, since the instruments are manip-

ulated through a trocar and because of the friction in

the trocar, the surgeon looses the sensation of the in-

teraction forces between the instrument and the organ

and his dexterity is thus reduced. An other applica-

tion of force control that could increase the dexterity

of the surgeon is force scaling. Indeed, for precise

manipulation tasks, a robotic device could provide the

surgeon with an augmented sensation of the interac-

tion forces between the instrument and the organ.

Comanipulation appears to be a good solution to over-

come these problems. Comanipulation is a direct in-

teraction between the surgeon and the robot: the in-

strument is manipulated simultaneously by the sur-

geon and by the robot. The main difference between

comanipulation and teleoperation is that no master

arm is needed to impose displacements to the robot.

So the complexity and the cost of a comanipulation

system may be lower since it involves only one me-

chanical system. Moreover, the use of a comanipu-

lation system may be more intuitive for the human

operator.

Different approaches have been studied concerning

the comanipulation. Some systems are able to impose

virtual constraints to the surgeon’s gesture which re-

strain the tool into a delimited area of the task-space

Cagneau B., Bellot D., Morel G., Zemiti N. and D’Agostino G. (2008).

AUGMENTED COMANIPULATION IN ROBOTIC SURGERY.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 47-54

DOI: 10.5220/0001053600470054

 SciTePress

and forbid the access to critical zones.

For example, in (Schneider et al., 2000), the sys-

tem PADyC has been presented. The clinical results

obtained with this system concern pericardial punc-

ture. It consists to remove pathological liquid from

the pericardium using a needle. PADyC can be used

under different control modes corresponding to the

degree of autonomy the surgeon wants. The robot is

controlled with a velocity loop and it imposes con-

straints on the surgeon to prevent damages on the sur-

face of the heart. These constraints are computed with

respect to the relative position between the needle and

the percutaneous access. Indeed, a model of the op-

eration’s area is created during a pre-operative phase.

This model is then used to derive the constraints ﬁeld.

Here no force control is used to perform the operation.

In (Jakopec et al., 2003), the Acrobot system is

used to assist the surgeon during an operation of knee

replacement. The main feature of this system is to im-

pose virtual constraints on the surgeon when he/she

cooperates with the robot. When the task has been

deﬁned with the planning software, the manipulator

is able to move freely the robot to the operations area.

If the surgeon moves the tool outside the deﬁned path,

the robot applies forces on the user to modify the cur-

rent trajectory. It has been clinically proven that the

preparation of bones surfaces are more accurate com-

paring to a classical operation. Once again, no force

control is performed with this system.

Moreover, some systems can exploit a measure of

forces. Therefore, there is no need to use models of

contacts to obtain the measure of distal forces. It is

also possible to derive constraints which are directly

based on the forces applied by the surgeon on the or-

gans.

In (Kazanzides et al., 1992), a force controller is used

so that the surgeon can guide the robot. The surgi-

cal tool is attached below a force sensor mounted on

the robot’s wrist. The force controller uses the mea-

sured forces to provide the reference to an inner ve-

locity control loop. When the desired force is null,

any applied force on the instrument causes the robot

to move in the direction of this force. So, the surgeon

can guide the robot by holding the tool.

In the same manner, the Surgicobot system

(Kochan, 2004) allows the surgeon and the robot to

manipulate the same drilling instrument for maxillo-

facial interventions. The surgeon can freely move the

instrument except in some predeﬁned space where the

robot generates restrictive forces in order to prevent

the surgeon from moving the instrument too close to

vital nerves.

In (Taylor et al., 1999), (Kumar et al., 2000)

and (Roy et al., 2002) augmented comanipulation ap-

proaches are presented: the surgeon holds a handle

mounted on the robot and the robot manipulates the

instrument in a way such as it exerts on the organ the

same force that the surgeon applies on the handle, but

scaled-down. Three different control laws using an

inner position/velocity control loop are compared in

(Roy et al., 2002). The best results are obtained with

an adaptive control law involving the estimation of

the environment’s compliance. However, when the

contact with the environment is lost, the estimation

becomes problematic. Another disadvantage of this

control law is that it requires differentiation of the

force applied by the surgeon on the handle which is

a noisy signal.

Even if beneﬁts presented in the above references are

important (e.g. gesture’s accuracy or the increase of

system’s safety), none of these systems allow the sur-

geon to feel an ampliﬁed version of the distal forces

acting between the tool and the organ.

In this paper, we present a control scheme for aug-

mented comanipulation with force feedback. The

main advantages of this control law is that it does not

require any knowledge of the environment nor differ-

entiation of a noisy signal. This approach is an exten-

sion of previous works (Zemiti et al., 2006) realized

in our laboratory.

The ﬁrst part of this paper is devoted to the proposed

control law for augmented comanipulation. This con-

trol scheme is proven stable thanks to a passivity

study in the second part. Experimental results with

a robot dedicated to minimally invasive surgery are

presented in the last part.

2 AUGMENTED

COMANIPULATION

2.1 Principle of the Approach

We present, hereafter, a robotic device in order to as-

sist the surgeon for accurate manipulation tasks re-

quiring human judgment and involving small interac-

tion forces between the surgical tool and the organ.

Therefore, the proposed device allows an augmented

comanipulation. It is a comanipulation system be-

cause the surgical instrument is held simultaneously

both by the surgeon and by the robot. We call it aug-

mented because the robot is controlled in such a way

that the surgeon is provided with an ampliﬁed sensa-

tion of the interaction forces between the instrument

and the organ. As a consequence, the instrument ap-

plies on the organ the same forces that the surgeon

would apply in a transparent mode but decreased by a

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

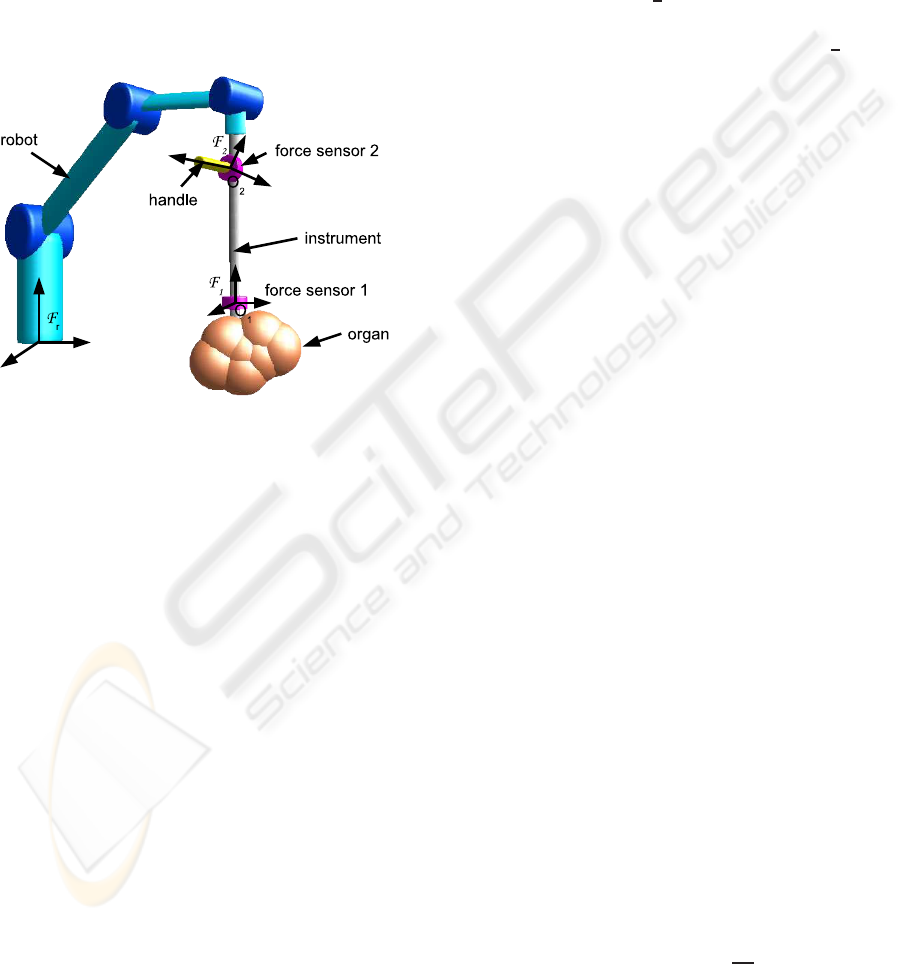
scale factor. This device can also ﬁlter the surgeon’s

tremor in order to increase the accuracy of the task.

This approach supposes that the reference forces pro-

vided by the surgeon and the interaction forces be-

tween the instrument and the organ may be measured

separately. Therefore a handle equipped with a force

sensor (force sensor 2) is mounted on the instrument

(see ﬁgure 1). The surgeon manipulates this handle

and the force sensor 2 measures the forces applied

by the surgeon on the instrument at point O

. The

force sensor 1 measures the forces applied by the or-

gan on the instrument at point O

. The data provided

Figure 1: Setup for augmented comanipulation.

by the force sensor number i are wrenches applied

on point O

and expressed in the basis of frame F

linked to the sensor. In order to be compared these

wrenches have to be expressed in the same point and

in the same basis. As the transformations between the

basis linked to frames F

and the basis linked to the

ﬁxed robot base frame F

are supposed to be known,

we choose to express the wrenches in the basis linked

to the frame F

. So, from the data provided by the

force sensor 1, we can compute −w

the wrench ap-

plied by the organ on the instrument at point O

and

expressed in frame F

. From the data provided by the

force sensor 2, we can compute −w

the wrench ap-

plied by the surgeon on the instrument at point O

and

expressed in frame F

. Note that w

and w

are respec-

tively the wrench applied by the instrument on the or-

gan at point O

and the wrench applied by the instru-

ment on the surgeon at point O

. Assuming that the

transformation between the frame F

and the frame

is known, we can compute the wrench −w

ap-

plied by the surgeon on the instrument at point O

: −w

= T

(−w

) with



−[O

]



where [O

]

denotes the skew symmetric matrix

associated with the vector from O

to O

expressed

in the basis of frame F

. However, in future work,

it will be interesting to compute this transformation

with a calibration process. In the Section 4, we as-

sume that the mechanical design is precise enough to

have a good estimation of this transformation.

With these notations, as detailed in subsection 2.3,

the aim of the proposed approach is to control the

robot such that w

= −

where β ∈]0;1] i.e. the

surgeon feels the forces applied by the organ on the

instrument, −w

, ampliﬁed by a scale factor

> 1.

The proposed control scheme is presented in the fol-

lowing subsection.

2.2 Proposed Control Scheme

The robot dynamics is modeled by the general form:

M(q) ¨q+C(q, ˙q) ˙q+ Γ

˙q+ G

(q) = τ − τ

− τ

(1)

where q ∈ R

denotes the joint positions, M(q) is the

positive deﬁnite symmetric inertia matrix, C(q, ˙q) ˙q is

a vector grouping the Coriolis and centrifugal joint

torques, Γ

˙q is a vector grouping the dissipative joint

torques, G

(q) is a vector grouping the gravity joint

torques, τ is the command vector for joint torques.

−τ

and −τ

are the joint torques corresponding re-

spectively to −w

and −w

i.e. −τ

= J

(q)(−w

)

and −τ

= J

(q)(−w

) where J(q) is the Jacobian

matrix of the robot at point O

, expressed in the basis

of F

At the lowest level of the controller, a proportionalve-

locity feedback is used in order to partially linearize

the robot dynamics:

τ = −B˙q+

(q) +

C(q, ˙q) ˙q+ τ

(2)

where B is a symmetric positive deﬁnite matrix of

feedback gains, τ

is the new command vector for the

joint torques,

(q) and

C(q, ˙q) ˙q are estimated val-

ues of G

(q) and C(q, ˙q) ˙q. Therefore, the model (1)

becomes:

M(q) ¨q+ B˙q = τ

− τ

(3)

The proposed control scheme is presented on ﬁg-

ure 2.

In this ﬁgure the Jacobian matrix J(q) is noted J.

This control scheme introduces notations deﬁned as

follow:

• C

(s) is a Proportional-Integral torque compen-

sator at the joint level such that:

(s) = K

(4)

where K

∈ R

n×n

and K

∈ R

n×n

are symmetric,

positive deﬁnite matrices.

AUGMENTED COMANIPULATION IN ROBOTIC SURGERY

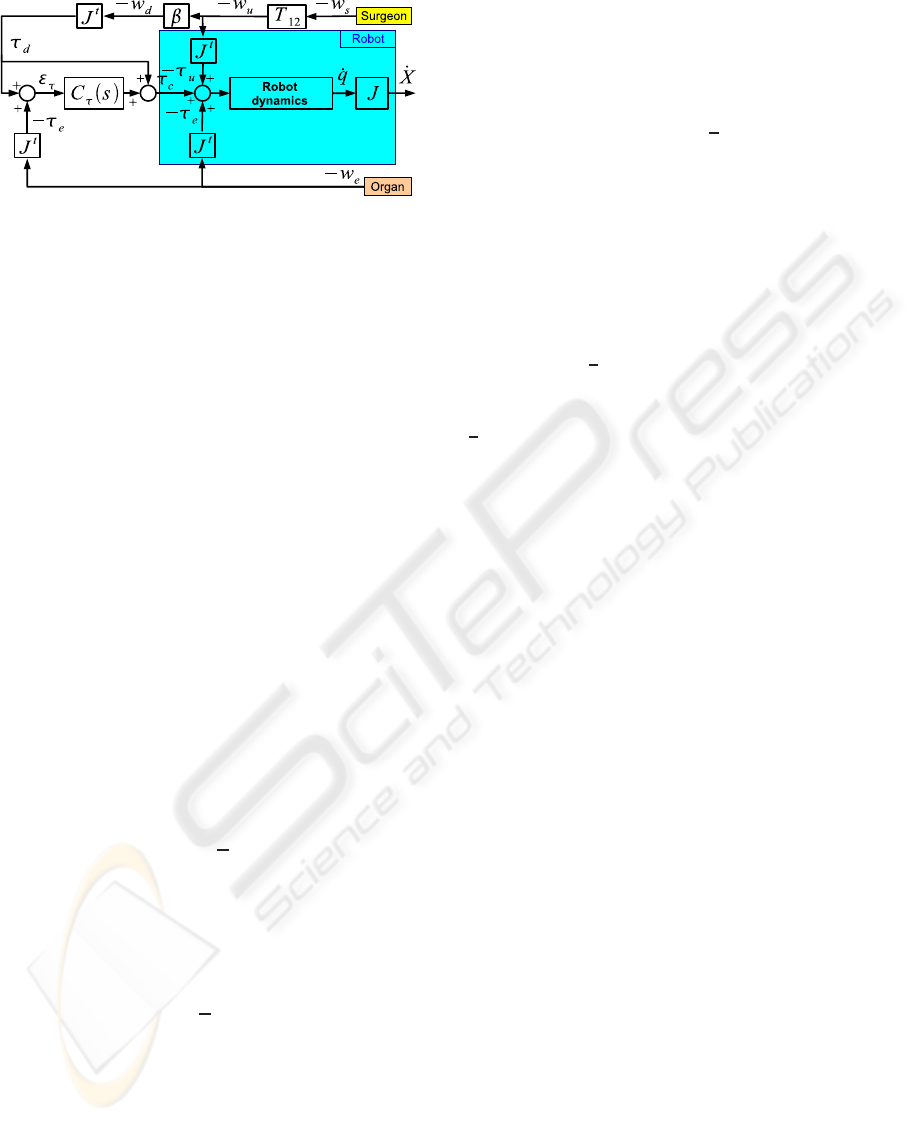
Figure 2: Augmented Comanipulation force control scheme

in joint space.

•

X is the 6-component vector grouping the coordi-

nates of the rotational and linear velocity of the

instrument at point O

with respect to frame F

expressed in the basis of F

In the sequel the following assumption will be

used :

Assumption 1 The matrix J(q) is of full rank n

This assumption means that the robot is not in a sin-

gular conﬁguration.

2.3 Equilibrium

The stability of the control scheme 2 will be proved in

the following section. So, assuming that this control

scheme is stable, as the controller C

(s) involves an

integral term, the torque error ε

will be null at the

equilibrium. So, at the equilibrium:

− τ

= 0 (5)

As the stable low-pass ﬁlter G(s) has a steady-state

gain equal to 1, at the equilibrium, τ

= J(q)

β(−w

Thus (5) leads to :

J(q)



(−w

) +

(−w

)



= 0 (6)

If n = 6 i.e. if we consider a 6 joints robot, the matrix

J(q) is square. Moreover, according to assumption

(1), this matrix is of full rank. Therefore, it can be

deduced from equation (6) that:

(−w

) (7)

Suppose that we choose β = 1. Then, equation (7) can

be written:

= (−w

) (8)

It means the wrench w

sensed by the surgeon at

point O

is such that its expression at point O

, w

, is

equal to the wrench −w

applied by the organ on the

instrument expressed at point O

. Thus the surgeon

manipulates the instrument in a transparent way i.e.

the surgeon senses the wrench w

as if he/she were

manipulating a zero mass instrument without any

friction.

Similarly, if β ∈]0;1[, equation (7) means that the

wrench w

sensed by the surgeon is an ampliﬁed

version, by the scale factor

> 1, of the wrench

that he would sense in a transparent manipulation.

Let’s remark that (7) can be written w

= β(−w

). It

means that the wrench applied by the instrument on

the organ at point O

is the wrench applied by the

surgeon at the same point, reduced by the scale factor

β.

If n < 6, J

(q) ∈ R

n×6

is not square. Thus it

cannot be deduced from (6) that the wrench error

= (−w

) +

(−w

) is zero. The wrench error ε

is not necessarily zero but belongs to the null space

of J

(q). An equilibrium is obtained between w

and

(−w

3 PASSIVITY

In the proposed approach, the robot interacts with its

environment. The stability of the control loop de-

pends not only on the robot dynamics but also on the

environment dynamics. However we cannot assume

for a known model for the environment. Therefore,

a useful tool for the stability analysis of the proposed

control loop is passivity analysis since this study does

not require any environments model. Thus, whatever

could be the contacts (robot-organ / robot-surgeon),

the passivity analysis ensures that the system remains

stable. The principle of a passivity study is presented

in the following subsection

3.1 Principle

Let consider an LTI system with an input u, an out-

put y, such that y = T(s)u with T(s) a real rational

transfer matrix. This system is passive if and only

if T(s) is positive real. In turn, positive realness can

be checked by the following property (Anderson and

Vongpanitlerd, 1973):

Property 1 Let s

= σ

+ jω

, k ∈ {1..m}, denote the

m poles of all the elements T

(s) of T(s), and let jω

l ∈ {1..p}, denote the p ≤ m pure imaginary poles of

all the elements T

(s) of T(s). The transfer T(s) is

Positive Real if, and only if:

1. ∀k ∈ {1..m},σ

< 0 ;

2. ∀l ∈ {1..p}, jω

is of multiplicity 1, and the as-

sociated residue matrix K

is hermitian, positive

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

semideﬁnite (PSD). The matrix K

can be com-

puted as:

= lim

s→ jω

(s− jω

)T(s) , if ω

is ﬁnite

and: K

= lim

s→∞

T(s)

, if ω

is inﬁnite

Note that a zero of T

(s) is considered as a pole

at the inﬁnity.

3. T

(− jω) + T( jω) = T

∗

( jω) + T( jω) is PSD, for

any ω ∈ R − {ω

,l ∈ {1..p}}. 

Let, now, consider an LTI system with two dif-

ferent inputs u

and u

provided by two different en-

vironments, and assume that this system is described

by: y = T

(s)u

+ T

(s)u

. This system is passive if

and only if T

(s) is positive real and T

(s) is positive

real.

3.2 Passivity of the Modiﬁed Force

Control Scheme

3.2.1 Modeling, Linearized Robot Dynamics

The robot controlled by the control scheme depicted

on ﬁgure 2 is a system whose output is

X. This sys-

tem has two inputs −w

and −w

provided by two

different environments, respectively the surgeon and

the organ. So, in order to study the passivity of this

system we ﬁrst have to compute the transfer matrix

(s) between −w

and

X and the transfer matrix

(s) between −w

and

X. This computation sup-

poses that the system is linear. Therefore, in order to

study the passivity of the proposed control scheme,

we linearize the robot dynamics (3) by assuming that

the robot evolves in a neighborhood of a given joint

conﬁguration q

so that we can set M = M(q

) con-

stant. The resulting linearized model writes:

˙q = Y

(s)(τ

− τ

) with Y

(s) = (Ms+ B)

−1

(9)

where s is the Laplace complex variable. More-

over, under the assumption that the robot evolves in

a neighborhood of a given joint conﬁguration q

, we

can set J = J(q

) constant. Then, we get the follow-

ing model:

X = Y

(s)(−w

) + Y

(s)(−w

) (10)

where:



(s) = JY

(s) [I

+ β(C

(s) + I

)]J

(s) = JY

(s) [I

+ C

(s)]J

3.2.2 Passivity Study

The system (10) is passive if and only if the matrices

(s) and Y

(s) are positive real. As J is supposed

to be of full rank (Assumption 1), this condition is

equivalent to the positive realness of the matrices Y

u,2

and Y

e,2

deﬁned as follow:



u,2

= Y

(s) [I

+ β(C

(s) + I

)]

e,2

= Y

(s)[I

+ C

(s)]

(11)

Equations (11), (9), and (4) lead to :







u,2

= (Ms+ B)

−1

+ βK

′

βK

e,2

= (Ms+ B)

−1

+ K

(12)

where K

′

= K

+ I

We ﬁrst derive conditions ensuring the positive re-

alness of Y

u,2

(s). The poles of Y

u,2

(s) are s

= 0 and

the poles of Y

(s). The poles associated to Y

(s) are

the solutions of det(Ms+ B) = 0 i.e. the eigenvalues

of −M

−1

B. As far as M and B are symmetric posi-

tive deﬁnite matrices, the eigenvalues of −M

−1

B are

negative real.

In order to check the second condition of property

1, we compute the residue K

associated to pole s

0. We get:

= lim

s→s

u,2

= βB

−1

As β > 0, we deduce the following condition for the

passivity of the control scheme:

−1

≥ 0 (13)

The third condition of property 1 consists in

checking, for any ω ∈ R − {0}, the positive semideﬁ-

niteness of the matrixH

( jω) deﬁned as follow:

( jω) = Y

u,2

( jω) + Y

u,2

(− jω)

= ( jωM+ B)

−1

+ βK

′

βK

jω

+ βK

′

βK

− jω

(− jωM+ B)

−1

(14)

because K

′

, K

, M and B are symmetric.

Positive semideﬁniteness of H

( jω) is equivalent

to positive semideﬁniteness of H

( jω) deﬁned as fol-

low:

( jω) =

( jωM+ B)H

( jω)(− jωM+ B)

+ K

′

jω

(− jωM+ B)

+( jωM+ B)

+ K

′

− jω

(15)

We get:

( jω) = R

+ R

+ jωIm

(16)

AUGMENTED COMANIPULATION IN ROBOTIC SURGERY

where:

= (2/β)B

= K

′

B+ BK

′

− (K

M+ MK

)

= MK

′

− K

′

= K

B− BK

The hermitian matrix H

( jω) must be PSD in order

to ensure passivity. Thus its real part has to be PSD

and its imaginary part has to be null. Therefore, the

following conditions have to be satisﬁed for any ω ∈

R − {0}:

+ R

≥ 0 (17)

ωIm

= 0 (18)

Thus, condition (18) is equivalent to:







+ R

≥ 0

= 0

(19)

To summarize, the matrix Y

u,2

(s) and thus Y

(s)

is positive real if and only if the following conditions

are satisﬁed:











−1

≥ 0

= 0

+ R

≥ 0

(20)

As far as positive realness of Y

e,2

(s) is concerned,

with a similar reasoning we deduce that the ﬁrst and

the second condition of property 1 are satisﬁed if and

only if M

−1

B > 0 and B

−1

≥ 0. It can be noticed

in equations (12) that the expression of Y

e,2

(s) is sim-

ilar to the expression of Y

u,2

(s) when β = 1 and K

′

is replaced by K

. Therefore, we deduce from equa-

tions (19) and (17) that the third condition ensuring

the positive realness of Y

e,2

(s) is satisﬁed if and only

if:







− K

M = 0

B− BK

= 0

B+ K

B− K

M ≥ 0

(21)

The equations (20) and (21) lead to the following

conditions for the passivity of the proposed control

scheme:











−1

≥ 0

− K

M = 0

B− BK

= 0

(

+ K

′

)B− K

M ≥ 0

(22)

with K

′

= K

+ I

4 EXPERIMENTS

The aim of these experiments is to show that it is pos-

sible to provide force feedback to the surgeon thanks

to proposed control scheme. Furthermore, for differ-

ent values of the gain β, we will verify that the sys-

tem remains stable. Experimentalsetup will be brieﬂy

described and beneﬁts of augmented comanipulation

will be evaluated experimentally.

Note that, in the rest of the paper, the used joint torque

compensator gains and the values of B and β were

chosen in such a way that the conditions given in 22

are veriﬁed.

4.1 Experimental Setup

The robot MC

E (French acronym for compact ma-

nipulator for endoscopic surgery) is a Kinematically

Defective Manipulator (KDM) which means that it

has fewer joints than the dimension of the space

in which its end-effector evolves. It is specially

suited for minimally invasive robotic surgery appli-

cations(Zemiti et al., 2007). With n = 4 joints and a

spherical structure, this robot provides 4 degrees of

freedom (DOFs) at the instrument tip.

The Figure 3 shows how the mechanical constraint

Figure 3: MC

E can comanipulate an instrument with a sur-

geon, and measures wrenches that are applied either by the

surgeon, or at the instrument tip.

is created. The lower part of the robot is dedicated to

the orientation of the instruments. The upper part al-

lows translation and rotation of the instrument along

its own axis.

Since the 4 axis coincide, there is a fulcrum point

which allows the insertion of the trocar into the pa-

tient’s body. This mechanical structure is clearly

adapted to Mini Invasive Surgery. Traumatisms are

reduced because translations through the fulcrum

point are not allowed.

Apart from its compactness, the main feature of

this robot is that it offers a possibility for force

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

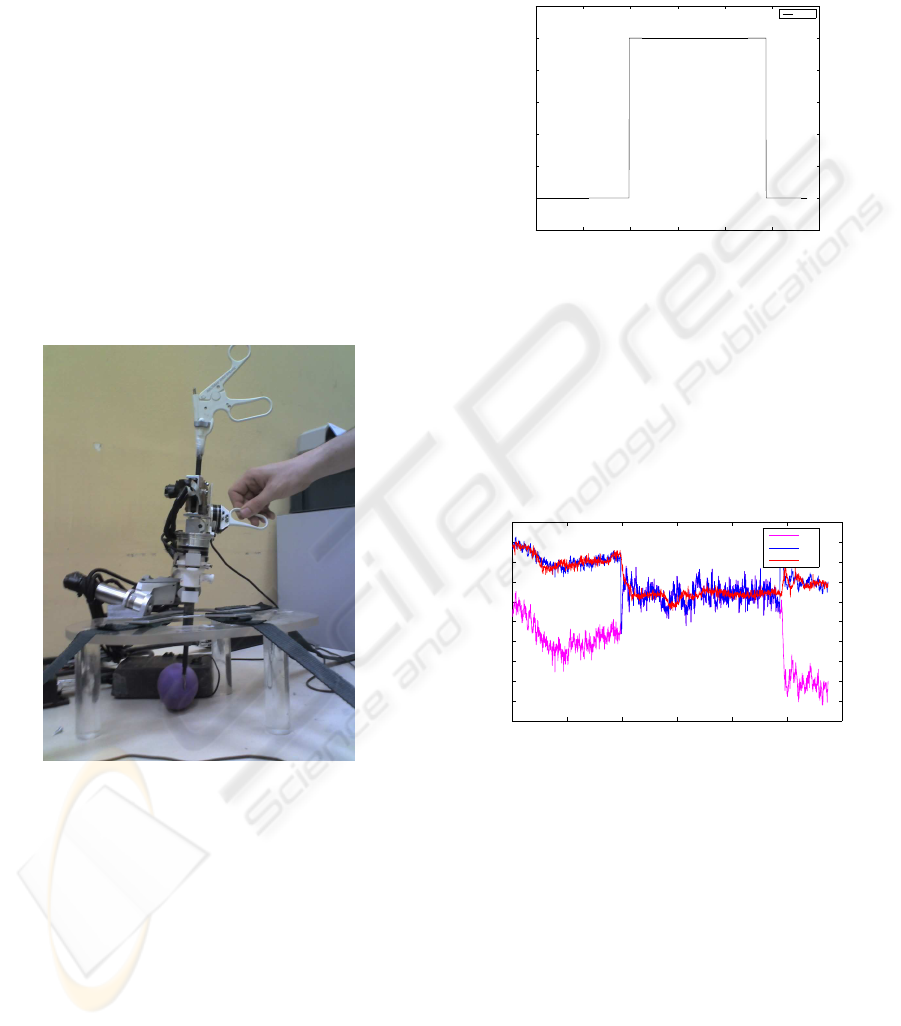
measurement in MIS. Namely, MC

E can measure

the distal organ-instrument interaction with a 6-axis

force-torque sensor placed outside the patient. Thus,

it is subject to much less sterilization constraints. Re-

markably, due to the special mounting of the force

sensor, these measurements are not affected by the

disturbance forces and torques arising from the inter-

action between the trocar and the instrument.

It is important to mention that the control scheme that

we have detailed in Section 2 can be used in other

ﬁelds of interest and not only in laparoscopic surgery.

For example, it is possible to improve surgeon accu-

racy during otologic surgery. The forces applied dur-

ing such kinds of interventions are very low. There-

fore, it should be useful to provide an ampliﬁed ver-

sion of these forces thanks to force feedback.

The new control scheme presented in section 2 indi-

cates that the robot interacts with two different envi-

ronments (the organ and the surgeon). This conﬁgu-

Figure 4: Experimental Setup.

ration is shown on ﬁgure 4. It needs a second force

sensor to measure forces between the robot and the

surgeon. Therefore to measure forces applied by the

surgeon, a second force sensor has been added on the

robot. Due to difﬁculties to ﬁx it directly on the han-

dle, it has been deported on the second axis of MC

This particular disposition was the quickest way to

provide force feedback to the manipulator. However,

the same disposition is not adapted to transmit forces

along instrument’s axis. In order to overcome this

problem, next step will be to modify existing experi-

mental setup to exploit each of the robot’s DOF.

4.2 Experimental Results

The ﬁgure 5 shows how the gain β has been modi-

ﬁed during the experiment. β = 1 is a particular value

0 2 4 6 8 10 12

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Time (s)

Gain values

Value

Figure 5: Gain values vs. time.

for which torques measured on the organ are equal

to torques applied by the manipulator. When setting

β = 0.5, torques applied on the organ should be de-

creased by a factor 2.

The ﬁgure 6 depicts torque measurements. It allows

to compare torques applied on the organ, torques pro-

vided to the controller and torques applied on the ma-

nipulator. This result demonstrates that the proposed

0 2 4 6 8 10 12

−0.6

−0.55

−0.5

−0.45

−0.4

−0.35

−0.3

−0.25

−0.2

−0.15

−0.1

Time (s)

Torques (N.m)

Figure 6: Torque values vs. time.

control scheme allows a reduction of the torques ap-

plied on the organ. At t = 10s, β is switched from 1.0

to 0.5. One can notify that torques applied on the or-

gan almost remain the same but torques applied by the

surgeon are ampliﬁed. Therefore, to apply the same

efforts on the organ, the surgeon must amplify forces

acting on the robot. This result satisﬁes equation (7).

The ﬁgure 7 shows that the system remains stable

for different values of gains. Furthermore, it demon-

strates that good performances can be achieved with

the controller which has been proposed in section 2.

Error appearing on Figure 7 is mainly due to noise

on measurement. However, one can notice that there

are some error peaks on this plot. This phenomenon

is due to the modiﬁcation of the force feedback gain

AUGMENTED COMANIPULATION IN ROBOTIC SURGERY

0 2 4 6 8 10 12

−0.2

−0.15

−0.1

−0.05

0.05

0.1

0.15

Time (s)

Torque (N.m)

Error

Figure 7: Torque error vs. time.

during experiments. In practice, if a ﬁxed value of β

is used, these peaks would not appear.

5 CONCLUSIONS

This paper presents a modiﬁed version of a force con-

trol scheme. In the context of comanipulation, it is

possible to provide force feedback to the manipula-

tor by modifying torques reference. In order to obtain

such results, a second force sensor is necessary to dis-

tinguish manipulator and environment forces.

Robots kinematic has been used to deal with

torques equilibrium. In other words, using a gains

matrix allows reduction of forces acting on the envi-

ronment and ampliﬁcation of forces acting on the ma-

nipulator. Experiments have been conducted to show

efﬁciency of the proposed control scheme.

Moreover, a formal proof of passivity has been es-

tablished. It ensures stability of the system whatever

could be contacts between the robot and its environ-

ment.

In future work, in-vivo experiments will be con-

duced. Even if experiments are satisfying with actual

experimental setup, it should be modiﬁed to exploit

the last 2 DOFS. A new handle seems to be the easi-

est way to use existing robot.

ACKNOWLEDGEMENTS

Barth´elemy Cagneau would like to acknowledge

Clara Lord for her contribution to this work. Scien-

tiﬁc and technical discussions have been very useful

to improve the quality of this paper.

REFERENCES

Anderson, B. D. and Vongpanitlerd, S. (1973). Network

Analysis and Synthesis -A Modern Systems Theory

Approach-. Englewood Cliffs, N.J. , Prentice-Hall.

Jakopec, M., Baena, F., Harris, S., Gomes, P., Cobb, J., and

Davies, B. (2003). The hands-on orthopaedic robot

acrobot: Early clinical trials of total knee replacement

surgery. IEEE Transactions on Robotics and Automa-

tion, 19(5):902–911.

Kazanzides, P., Zuhars, J., Mittelstadt, B., and Taylor, R. H.

(1992). Force sensing and control for a surgical robot.

In Proceedings of the IEEE International Conference

on Robotics and Automation, pages 612–617.

Kochan, A. (2004). A cobotic solution for surgical appli-

cations. Industrial Robot: An International Journal,

31:478–480.

Kumar, R., Berkelman, P., Gupta, P., Barnes, A., Jensen,

P. S., Whitcomb, L. L., and Taylor, R. H. (2000).

Preliminary experiments in cooperative human/robot

force control for robot assisted microsurgical manipu-

lation. In Proceedings of the IEEE International Con-

ference on Robotics and Automation, pages 610–617.

Roy, J., Rothbaum, D. L., and Whitcomb, L. L. (2002).

Haptic feedback augmentation through position based

adaptive force scaling: theory and experiment. In Pro-

ceedings of the IEEE/RSJ International Conference on

Intelligent Robots and Systems, pages 2911–2919.

Schneider, O., Troccaz, J., Chavanon, O., and Blin, D.

(2000). Padyc: a synergistic robot for cardiac punctur-

ing. In Proceedings of the IEEE International Confer-

ence on Robotics and Automation, pages 2883–2888.

Taylor, R., Jensen, P., Whitcomb, L., Barnes, A., Kumar, R.,

Stoianovici, D., Gupta, P., Wang, Z., deJuan, E., and

Kavoussi, L. (1999). A steady-hand robotic system for

microsurgical augmentation. International journal of

robotics research, 18:1201–1210.

Zemiti, N., Morel, G., Micaelli, A., Cagneau, B., and Bel-

lot, D. (2006). A passive formulation of force con-

trol for kinematically constrained manipulators. In

Proceedings of the IEEE International Conference on

Robotics and Automation, pages 2238–2243.

Zemiti, N., Morel, G., Ortmaier, T., and Bonnet, N. (2007).

Mechatronic design of a new robot for force control in

minimally invasive surgery. IEEE/ASME Transactions

on Mechatronics, 12(2):143–153.

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices