APPLICATION OF WEIGHTED LEAST SQUARES TO

CALIBRATE A DIGITAL SYSTEM FOR MEASURING THE

RESPIRATORY PRESSURES

José Leonardo Ferreira, Nadja Carvalho Pereira, Marconi de Oliveria Júnior, João Lucas da Silva

Flávio Henrique Vasconcelos, Carlos Julio Tierra-Criollo

Department of Electrical Engineering, UFMG, Av. Antônio Carlos 6627, Belo Horizonte, Brazil

Raquel Britto, Verônica Franco Parreira

Department of Physiotherapy,UFMG, Av. Antônio Carlos 6627, Belo Horizonte, Brazil

Keywords: Calibration, measurement uncertainty, respiratory pressures measuring, weighted least squares.

Abstract: This article presents the results associated to calibration and evaluation of the measurement uncertainty of a

digital respiratory pressures measuring system developed at the Biomedical Engineering Research &

Development Laboratory (NEPEB) of the Department of Electrical Engineering – UFMG. The proposed

method uses the least squares weighted regression to establish the measurement model and to evaluate the

uncertainty. The standard expanded uncertainty estimated by the model was 1.4 kPa.

1 INTRODUCTION

The qualitative and quantitative characterization of

the result of a measurement is a demand of

metrology organisms, providing knowledge about

the reliability, important to quality control of

products and services. In Brazil, the National

Institute of Metrology, Standardization and

Industrial Quality (INMETRO) is the local NMI

(national measurement institute) and as such is

organism responsible for metrology politics and for

establishing criterions and general normalization

relative to expression of uncertainty (INMETRO,

2007).

Brazilian Ministry of Health (MS) established

the compulsory certification for medical and hospital

equipment (MHE), not only attributing conditions

for a major credibility of use, but, also causing a

huge demand for calibration services in the country.

A non-calibrated medical equipment can lead clinic

diagnostic errors, wrong therapies and iatrogeny in

patients.

Today, regulation of certification process of

MHE quality in Brazil is defined by two normative

documents: MS and ANVISA (1999) and MIDIC

and INMETRO (2006). The former defines the

strategies, while the latter describes the technical

details for certification.

A digital system was developed at NEPEB

(Silva, 2006) in order to measure the maximum

pressures exerted by the muscles of the human

respiratory system. It was designed as equipment to

be used in diagnostic and therapy and, therefore,

must be submitted to metrological evaluation

according to the standards of the MS. Thus, the

measuring system must be certificated, and this

process requires instrument calibration and the

evaluation of the measurement uncertainty.

The measuring system includes a signal

acquisition module for pressure and an analogical to

digital signal conversion module that allows the

digital data to be acquired using a personal computer

(PC) through an USB interface.

2 OBJECTIVES

The signal acquisition module of pressure,

denominated manovacuometer, uses two sensors of

differential pressure, model MPX5050 by Freescale

Semicondutor Inc. (Austin, Texas). The sensor

possesses two pressure sides (figure 1) and the

measured value corresponds to the differential

220

Leonardo Ferreira J., Carvalho Pereira N., de Oliveria Júnior M., Lucas da Silva J., Henrique Vasconcelos F., Julio Tierra-Criollo C., Britto R. and Franco

Parreira V. (2008).

APPLICATION OF WEIGHTED LEAST SQUARES TO CALIBRATE A DIGITAL SYSTEM FOR MEASURING THE RESPIRATORY PRESSURES.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 220-223

DOI: 10.5220/0001052602200223

 SciTePress

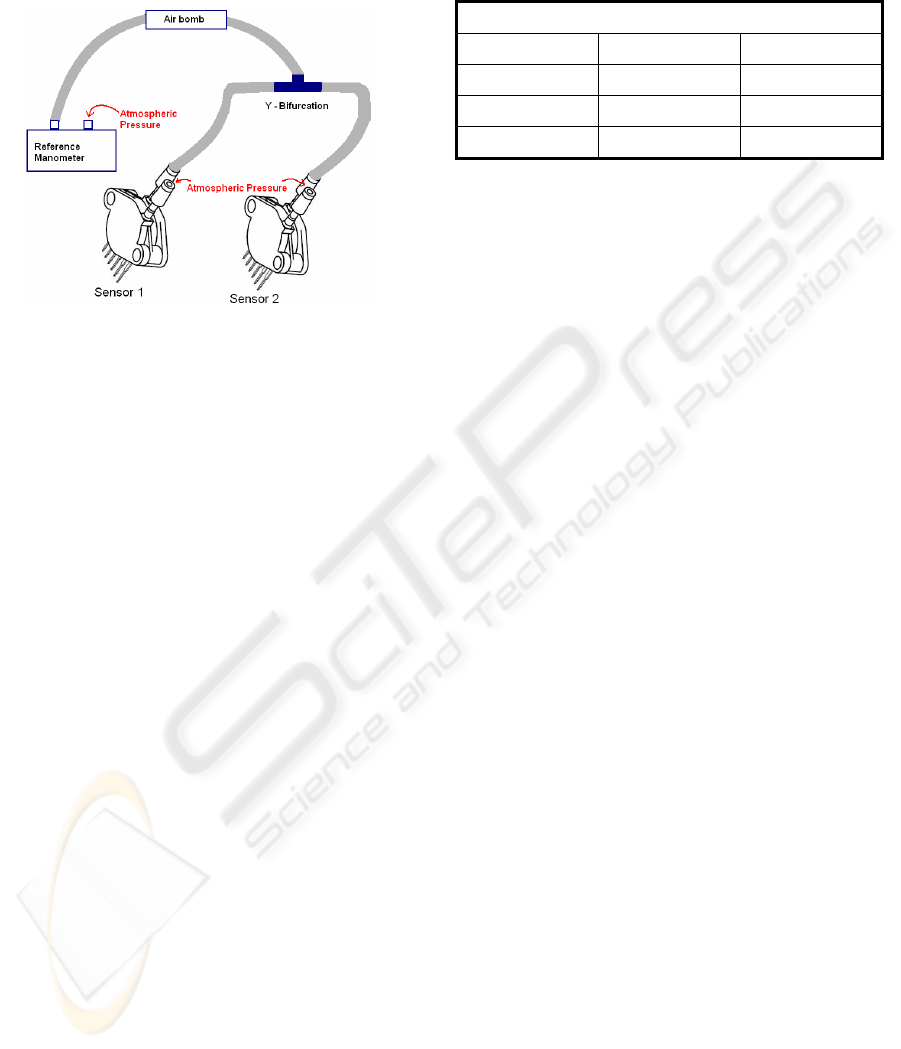
pressure taken between the two sides. Nevertheless,

it is important to emphasize that pressure in one side

(P1) must be always higher than that in the other

side (P2).

Figure 1: Schematic implementation for prototype

calibration.

The purpose of this work is to carry out the

calibration of digital manovacuometer developed by

NEPEB. The proposed metrological model was built

using the weighted least squares method, and, in that

way, the measurement uncertainties was evaluated.

3 METHODOLOGY

3.1 Calibration Measurement System

Protocol

In order to carry out the calibration of the digital

manovacuometer, the protocol describe in

(INMETRO, 1997) was used. Two were the

motivation for the use of that procedure: (i) the

sphygmomanometers with aneroid manometer was

one of few clinic equipments that have

normalization, regulation and control by INMETRO;

(ii) although the normalization is specific for

sphygmomanometers with aneroid manometer, this

refers to the same type of physical quantity

measured by the manovacuometer.

Tests were implemented to get the calibration

curves for the two sensors of the developed

equipment: i) the maximum indication error test and

ii) the hysteresis test.

According to that procedure, the pressure applied

to the sensors has to be increased and thereafter

decreased. The pressure values (table 1) were

applied during approximately five seconds, and an

average voltage was evaluated at the output of the

manovacuometer. The tests were performed four

times, and a curve of the output voltage versus

applied pressure, for each sensor, was plotted.

Table 1: Reference pressure values applied to prototype.

Pressure (kPa)

4.0 9.3 12.0

13.3 20.0 26.7

33.3 40.0 46.7

53.3 60.0 –

Curve fitting was implemented using the method of

weighted least squares (ABNT and INMETRO,

2003; Lira, 2002; Mathioulakis and Belessiotis,

2000; Press et al., 1992). It was chosen to make the

fitting for the average rising and fall curves of each

sensor. Hence, two curves (rising and fall) were

obtained for each sensor.

The instrument which measure the pressure

applied to the prototype was a digital commercial

manovacuometer (reference manometer) by Ecil

(model BB480003) with reported maximum

uncertainty of 0.03% (k=2), traceable to the SI

standard. In figure 1, it is illustrated the schematic

for calibration of the prototype, built in our

laboratory.

3.2 Evaluating Measuring Uncertainty

Protocol

The proposed model to calculate the measuring

uncertainty, u

, which is associated to the pressure

corrected value, was built using the regression fitting

obtained with the weighted least squares method.

The u

and the uncertainty of the reference mano-

vacuometer lead to the evaluating of the standard

combined uncertainty u

(P) and, consequently, to the

expanded uncertainty U

of the measured pressure

with the prototype for a test pressure of 26.7 kPa.

4 RESULTS

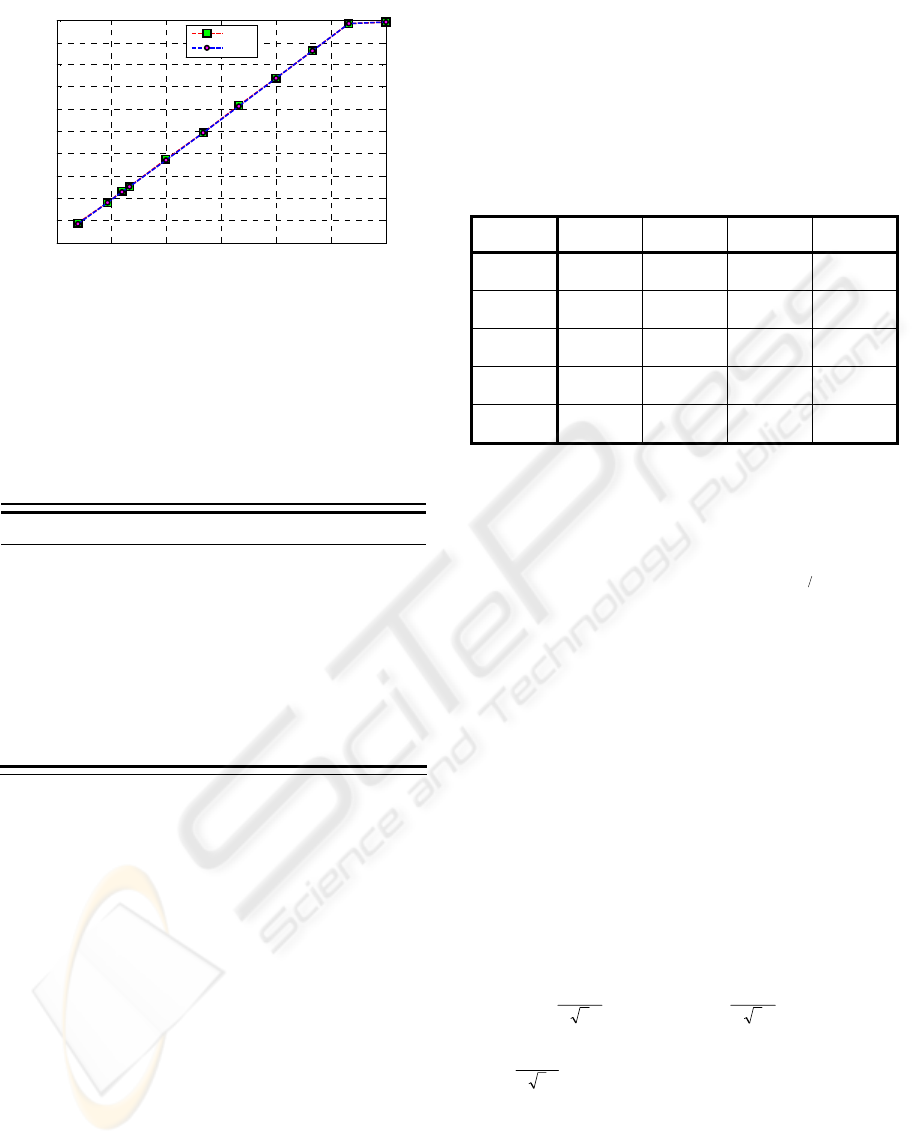
Figure 2 shows the average calibration curves (rising

and fall) for sensor 1 of the manovacuometer under

calibration (similar calibration curves to sensor 2).

For fitting implementation, the linear region (up to

53.3kPa) was used. For each calibration curve, the

fitting was approximated by the equation:

mrc

aVbP +=

(1)

where P

corresponds to pressure given a voltage on

the output of the manuovacuometer (V

) under

calibration.

APPLICATION OF WEIGHTED LEAST SQUARES TO CALIBRATE A DIGITAL SYSTEM FOR MEASURING THE

RESPIRATORY PRESSURES

221

0 10 20 30 40 50 60

0.5

1.5

2.5

3.5

4.5

Calibration Curves for Sensor 1

Pressure (kPa)

Voltage (V)

Rising

Fall

Figure 2: Calibration average curves for sensor 1.

In table 2, are given the reference pressure values

associated to measured output voltage values

(calibration points) and the respective standard

combined uncertainty to rising curve of sensor 2.

Table 2: Reference pressure and output voltage values and

associated uncertainties – sensor 2 (rising curve).

(kPa) u

(kPa) V

(V) u

(V)

4.0 0.0006 0.4578 0.0024

9.3 0.0014 0.9257 0.0066

12.0 0.0018 1.1753 0.0022

13.3 0.0020 1.2909 0.0036

20.0 0.0030 1.8904 0.0035

26.7 0.0040 2.4955 0.0050

33.3 0.0050 3.0974 0.0047

40.0 0.0060 3.7094 0.0045

46.7 0.0070 4.3333 0.0034

53.3 0.0080 4.9410 0.0050

The uncertainty u

associated to reference

manovacuometer, was evaluated using the value of

the related standard expanded uncertainty, as long as

the uncertainty u

was estimated based on

fluctuation of the repeated readings in each

calibration point (Mathioulakis and Belessiotis,

2000), correspondent to type A uncertainty.

The mathematics of linear regression fitting

using weighted least squares is described with more

details in Lira (2002), Mathioulakis and Belessiotis

(2000) and Press et al. (1992). The slope a and the

intercept b as well as the associated uncertainties u

e u

can be obtained from:

(

)

LKCKK

⋅=⋅⋅

(2)

where, C is a vector whose elements are the fitted

coefficients a and b; and W=(K

.L)

-1

is a matrix

whose diagonal elements are the variances of a (w

2,2

)

and b (w

1,1

). The off-diagonal elements w

1,2

2,1

are

the covariances between these parameters. K and L

are a matrix and a vector, respectively, whose

elements are weighted by pounds that depend on the

uncertainties u

and u

. Solving (2), one obtains

the parameters and their uncertainties for each

average curve. The results are shown in table 3.

Table 3: Values for the parameters a and b and its

uncertainties u

and u

Sensor 1 -

Rising

Sensor 1 -

Fall

Sensor 2 -

Rising

Sensor 2 -

Fall

(kPa/V)

10.9747 10.9797 11.0159 10.9747

(kPa/V)

0.0050 0.0034 0.0086 0.0026

(kPa)

-0.5845 -0.5280 -0.9506 -0.7989

(kPa)

0.0169 0.0079 0.0206 0.0077

Cov(b,a)

(kPa/V)

-7.44x10

-5

-2.13x10

-5

-1.43x10

-4

-1.71x10

-5

Calculation of the uncertainty u

associated to

calibration points is derived from the law of

propagation of uncertainties (ABNT and

INMETRO, 2003) and equation (1):

(

)

22222

),(2 abCovVuVuuau

mambVPc

+++=

(3)

The standard combined uncertainty, in turn, was

obtained by:

)(

uuPu

(4)

where u

is the uncertainty associated to reference

manovacuometer.

The measuring uncertainty was calculated in

relation to a calibration point (26.7 kPa) arbitrarily

chosen of the average rising curve of the sensor 2.

To this point, the average output voltage is

= 2.4955 V. The uncertainty u

is estimated

considering the type A uncertainty, u

, the sensor

accuracy, u

, and the resolution of manovacuometer

under calibration, u

0050.0

0100.0

0650.0

1125.0

00006.0

0001.0

Vuuuuu

VmREVVm

0652.0

2222

=⇒++=

Taking account these values, those of third column

of table 3 and (3) result u

=0.7183 kPa. For the

reference pressure of 26.7 kPa, the value of u

equal to 0.0040 kPa. Hence, the standard combined

uncertainty is estimated as 0.7 kPa. Finally, the

value for the standard expanded uncertainty is

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

222

evaluated using the expression of Welch-

Satterthwaite (ABNT and INMETRO, 2003).

For the confidence interval of 95.45%, the obtained

value for the effective number of degrees is ν

eff

→∞,

which indicates a coverage factor of k=2. Therefore,

the estimated value for the standard expanded

uncertainty is equal to U

=1.4 kPa.

5 DISCUSSIONS

The repeatability of measurement of calibration

curves, as discussed in other works of NEPEB, was

confirmed here. The maximum value obtained for

the type A uncertainty associated to the values of V

is equal to 0.0066 V.

Calculations of hysteresis were performed

considering the fitting curves. The maximum

absolute value obtained for hysteresis was equal to

0.1467 kPa for sensor 1 and 0.2957 kPa for sensor 2.

These values are much lower than the value

established by INMETRO for sphygmomanometers

with aneroid manometer. In the same way, when is

considered the linear region, it is noticed that the

results obtained in maximum indication error test are

also inside the tolerance range determined by

INMETRO for this equipment (0.4 kPa).

The standard combined and expanded

uncertainties estimated for the prototype (for

reference pressure of 26.7 kPa) were 0.7 kPa and

1.4 kPa, respectively. The last value is lower than

that suggested in INMETRO (2006) for analogical

pressures measuring systems, that is, 12 kPa.

6 CONCLUSIONS

The proposed model to calibrate the digital

manovacuometer developed at NEPEB uses the

weighted least squares. This model indicates that the

hysteresis, maximum indication error and

uncertainty of the prototype were inside the

tolerance range established by INMETRO.

In future works it must be investigated and

inserted to the proposed metrological model other

possible factors that can be influencing the result

prototype uncertainty, as those associated to A/D

converter, temperature variation and correlation

between the curves parameters and input pressure.

ACKNOWLEDGEMENTS

To FAPEMIG and CNPq for financial support. To

CETEL/SENAI/FIEMG represented for Luiz

Henrique, Marcus Vinicius and Reiner that lent the

laboratory and reference manovacuometer for the

measurements. To Rômulo Martini of FHEMIG.

REFERENCES

ABNT; INMETRO, 2003. Measurement uncertainty guide

(free translation). ABNT, INMETRO, Rio de Janeiro.

Brazilian Ministry of Development, Industry and Foreign

Commerce (MIDIC); INMETRO, 2006. Establishes

the evaluation of conformity for MHE. Portaria N

de 3 de abril de 2006.

Brazilian Ministry of Health (MS); Brazilian National

Health Vigilance Agency (ANVISA), 1999.

Establishes the certification for MHE. Resolução N

444 de 31 de agosto de 1999.

INMETRO, 2007. Homepage: http://www.inmetro.gov.br

INMETRO, 1997. Procedure for verification of the

sphygmomanometers with aneroid manometer (free

translation). INMETRO, Rio de Janeiro.

INMETRO, 2006. Guidelines to carry out the calibration

of analogical system measuring pressure (free

translation). INMETRO, Rio de Janeiro.

Lira, I., 2002. Evaluating the measurement uncertainty:

fundamentals and practical guidance. Bristol and

Philadelphia: IoP.

Mathioulakis, E.; Belessiotis, V. 2000. Uncertainty and

traceability in calibration by comparision. Meas. Sci.

Technol., 11: 771-775

Press, W.; Teukolsky, S.; Vetterling, W; Flannery, B.

1992. Numerical recipes in C: the art of scientific

computing. 2nd ed. Cambridge University Press,

Cambridge, 2

edition.

Silva, J, 2006. Development of a digital system for

measuring maximum respiratory pressures (free

translation). Monografia (Bacharelado em Engenharia

de Controle e Automação) – Escola de Engenharia,

Universidade Federal de Minas Gerais, Belo

Horizonte.

APPLICATION OF WEIGHTED LEAST SQUARES TO CALIBRATE A DIGITAL SYSTEM FOR MEASURING THE

RESPIRATORY PRESSURES

223