MICRO-SHAFT-POKING

A Novel Instrument for Mechanically Characterizing Soft Biomimetic Membrance

Kuo-Kang Liu, Mark Ahearne, Eleftherios Siamantouras and Ying Yang

Institute of Science Technology in Medicine, Keele University, Stoke-on-Trent, UK

Keywords: Instrumentation, hydrogel, mechanical characterization, microengineering.

Abstract: Characterizing viscoelastic properties of soft biomimetic membranes has become increasingly important due

to their biomedical applications such as tissue engineering/regenerative medicine and biosensors. This paper

presents a new micro-shaft-poking (MSP) technique which is free from the complication of substrate

backing, normally occurred as an intractable problem in the conventional indentation testing for soft

membranes. A tailored indention apparatus with a spherical indenter was constructed to achieve the force

resolution and displacement of 1μN and 1μm. The biomimetic membranes which were used for mechanical

testing were made of two types of hydrogel, alginate and agarose. The results showed that the elastic

modulus increased with gel concentration. A creep test has also been conducted to examine the time-

dependent behaviors of various hydrogel and a viscoelastic model has been correspondingly developed and

applied to describe the experimental results. Other potential applications of this new instrument to other

membranes, both artificial and biological, have been addressed in the paper.

1 INTRODUCTION

Recent advancements in biomimetic materials have

opened a new avenue for tissue regeneration/implant

and the construction of next generation biomedical

devices, such as developing engineered tissue and

designing cell-based biosensor. In many cases, their

viscoelastic/mechanical properties play an important

role in the performance and durability of these

membranes, and ultimately dictate whether the

applications are successful or not. A great need

therefore is required for the development of new

techniques for mechanically characterizing these

emerging biomimetic materials such as hydrogels

(Ratner et al., 1996). However, mechanical

characterization of these materials in a quantitative

manner is highly challenging due to their unique

mechanical characteristics, such as fragility and

viscoelasticity

Despite the intractability in experimentally

measuring the mechanical properties of soft

biological materials, recent progress in the advanced

instrument developments have made such

microscale characterization more feasible (Lu et al.,

2004). The common fundamental principle among

these advanced methods is to measure the material

deformation under an applied load. Among these,

bulge or blister testing, nanoindentation, and

microtensile testing are prevailingly used for

mechanical characterization of soft biomimetic

materials (Espinosa, et al., 2003; Liu et al., 2004).

Testing via bulging or nanoindentation alleviate

many of the problems such as mounting specimen

and providing sufficient resolution of measurements

(Scott et al., 2004). Moreover, the data measured by

using different testing techniques are often scattered.

Such variations have been recognized to be

attributed to the technological means employed by

each technique and the calibration. Also the different

requirements for conducting the experiments and

interpretation of results will also contribute to the

diecrepancy (Liu et al, 2004; Menciassi et al., 2001).

Therefore the mechanical properties of the soft

materials are difficult to be unequivocally

determined when the various techniques are

compared (Espinosa et al., 2003).

In this work, a new ultra-precise measuring

instrument, the MSP, for characterizing mechanical

properties of biomimetic materials are described.

Based on simultaneous force-displacement

measurements, the elastic modulus of soft

membranes can be determined. This instrument

provides a broad range of measurements to facilitate

large deformation analysis as well as time dependant

210

Liu K., Ahearne M., Siamantouras E. and Yang Y. (2008).

MICRO-SHAFT-POKING - A Novel Instrument for Mechanically Characterizing Soft Biomimetic Membrance.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 210-215

DOI: 10.5220/0001051402100215

 SciTePress

force measurements, with microscale resolution.

Firstly, the testing technique has been used to

characterize circular biomimetic hydrogel

membranes whose properties are of great interest for

biomedical applications and have not been

investigated well before.

2 EXPERIMENTAL SETUP

2.1 Instrumental Setup

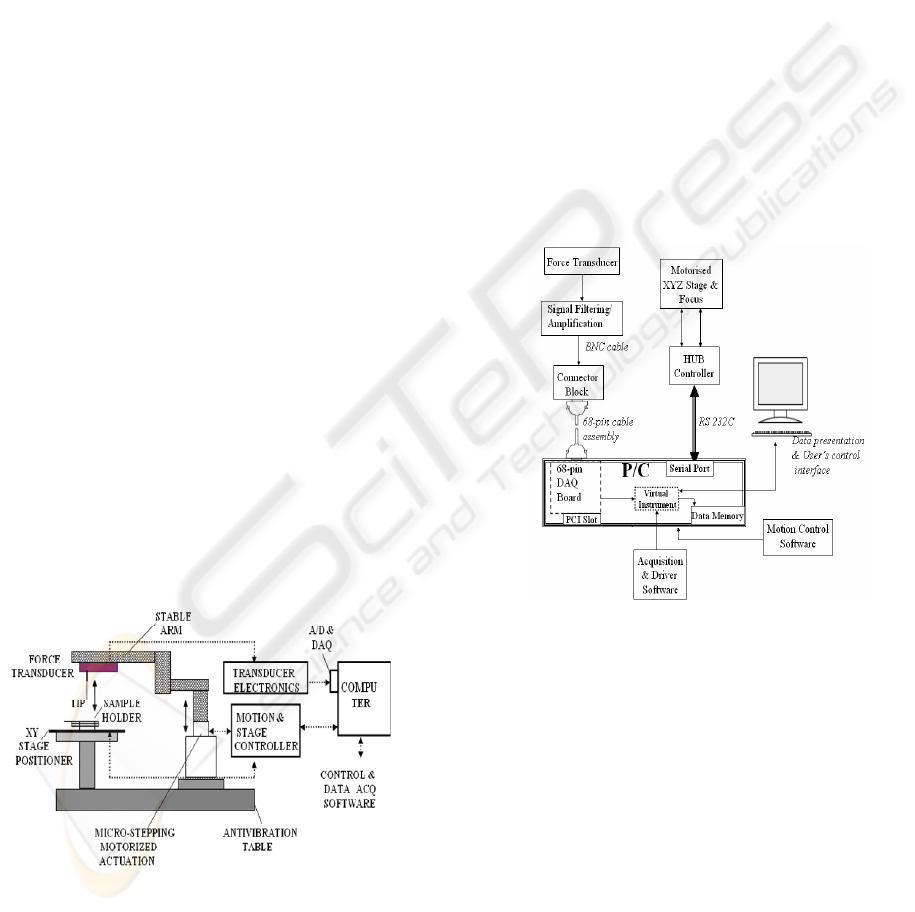
The system, schematically shown as Figure 1, was

newly developed for measuring force as a function

of displacement. The instrument is based around an

inverted optical microscope (Eclipse TE 2000S,

Nikon, USA), incorporated with a XYZ motorized

motion control interfaced with as external PC. The

microscope’s Z-axis motorized stage, which is

capable of 1μm step and a travelling distance up to

8.5mm, is used as a displacement actuator (ESP300,

Newport, Irvine, CA). Attached to Z-axis stage was

a specially designed solid arm, on which edge a

force transducer (404A, Aurora Scientific Inc.,

Canada), with 1μN force resolution and 100mN

maximum force capability, was mounted firmly. The

stability of the arm prevents from the “dead” weight

effect of the transducer’s head in the output signal

and avoids bending of the interior housing of the

transducer, which might offset the output. In

addition, it ensures precise loading in a vertical

position. In the final form the instrument had a force

and displacement resolution of 1μN and 1μm

respectively.

Figure 1: Schematic view of the instrumental set-up (not

to scale).

A fine, spherical tip is attached at the end of the

force transducer’s output tube for deforming the

sample. A handy sample holder facilitates mounting

of a thin, circular membrane between a set of

parallel plastic rings, without affecting the natural

properties of the material. The position of the

membrane for central alignment can be adjusted

precisely by tuning a two dimensional (X-Y)

translation stage (ASSY STAGE 25, Cell Robotics

Inc., USA), with a resolution higher than 2μm. The

force transducer signal is filtered and amplified by

using differential amplification (S 400A, Aurora

Scientific Inc., Canada). The amplified analogue

signal is transmitted through a connector block

(DAQ SCB-68, National Instruments, USA) into a

data acquisition (DAQ) board (PCI DAQ-6036E,

National Instruments, USA) for digitization and

further processing. The acquired data were displayed

and recorded by a tailored software design based on

the Labview platform (National Instruments, USA).

Figure 2 shows the interconnections among

instrumentation, data acquisition and control.

Figure 2: A block diagram of the system showing the

interconnections between instrumentation, data acquisition

and control interface.

2.2 Material Preparation

Two types of hydrogel, alginate and agarose, were

prepared. Alginate is a co-polymer consisting of β-

D-mannuronic (M block) and α-L-guluronic (G

block) acid. The ratios and lengths of these blocks

play an important role in the mechanical behaviours

of the alginate. A 2% (w/v) solution of sodium

alginate was formed by dissolving 2 g of Protanal

LF200 S (FMC BioPolymer, Norway) in 100 ml of

deionised water. The ratio of M block to G block in

this type of alginate has been found to be 0.23

(Drury et al., 2004). Different concentrations of the

MICRO-SHAFT-POKING - A Novel Instrument for Mechanically Characterizing Soft Biomimetic Membrance

211

alginate solution were formed by adjusting the ratio

of alginate powder to deionised water. When fully

dissolved, the solution was autoclaved for

sterilization. Autoclaving had the effect of

decreasing the viscosity of the solution. To fabricate

alginate hydrogels, rings made from filter paper

(Millipore, USA) were placed on the bottom of

small petri dish. These rings reduced the amount of

shrinkage of the hydrogel after crosslinking and

allowed the hydrogels to be lifted from the petri

dishes. 200 µl alginate solution was poured inside a

ring of inner diameter 11 mm. 5 ml of 0.5 M filtered

calcium chloride solution (CaCl

) was added over

the alginate. The application of CaCl

caused the

sodium in the alginate to be replaced by calcium,

which resulted in crosslinking and formation of a

hydrogel. Once applied, the CaCl

solution had to

cover the alginate quickly to prevent the hydrogel

from forming unevenly. After 10 minutes the CaCl

solution was removed and the hydrogel was washed

twice in phosphate buffered saline (PBS) (Sigma,

UK).

Agarose hydrogels were made using agarose

type 1 (Sigma, UK). A 2% (w/v) agarose solution

was produced by dissolving 0.2 g of agarose powder

in 10 ml PBS. For lower concentrations, less

agarose powder was required. The powder was

dissolved by heating the solution to over 60°C.

When fully dissolved, the solution was filtered to

remove any impurities. 200 µl of the solution was

applied to a petri dishes with circular filter paper

rings of inner diameters 11 mm. The hydrogels

were formed by cooling at room temperature. Once

the hydrogel had formed, water or PBS was added to

the petri dish to prevent the agarose from

dehydrating.

3 THEORETICAL ANALYSES

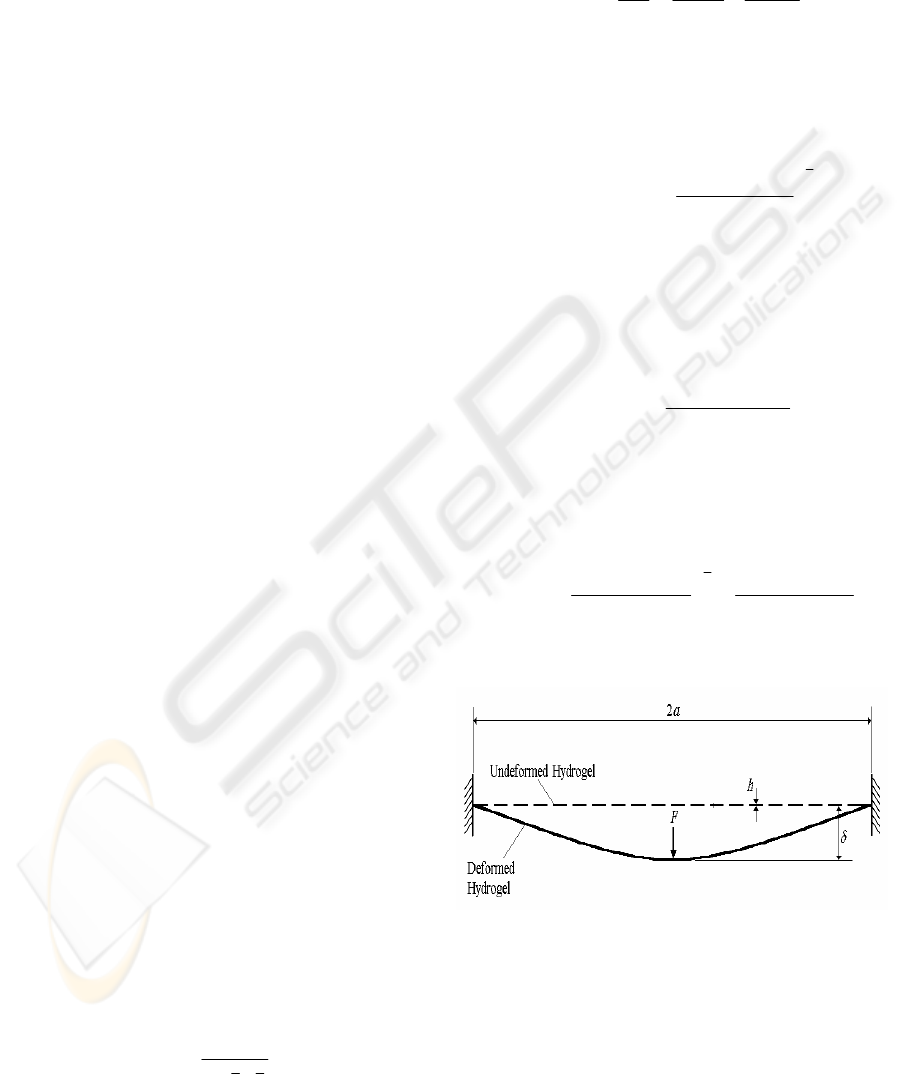
The Young’s modulus was calculated from the

indentation data using a previously described

theoretical model (Scott et al., 2004). For a

hydrogel material suspended around its outer edge

(Figure 3), the total displacement that the indenter is

lowered (δ) is equal to the sum of the depth of

penetration into the hydrogel (δ

) and the vertical

deformation displacement of the hydrogel (δ

). δ

can be calculated using the Hertz model (Johnson,

1985);

E =

(1)

where F is the force applied to the hydrogel by the

indenter, R is the radius of the indenter tip and E* is

the elastic modulus and can be derived from the

equation;

EEE

νν

−

(2)

where E

and E

are the moduli of the indenter and

hydrogel respectively and ν

and ν

are their

Poisson’s ratios. Since the modulus of the indenter

is much larger than the hydrogel, the term (1 - ν

)/E

was neglected and equation (1) can be rewritten as;

222

)1(9

⎟

⎠

⎞

⎜

⎝

⎛

−

(3)

where E and

are the Young’s modulus and

Poisson’s ratio of the hydrogel materials. The

vertical deformation displacement of the hydrogel

was calculated using plate-bending theory

(Timoshenko & Woinowsky-Krieger, 1959) from

the equation;

π4

)1(3

−

(4)

where h is the thickness and a is the radius of the

hydrogel inside the sample holder. By adding

equations (3) and (4), the total displacement of the

indenter on the bending-governing deformation was

determined from the equation;

222

π4

)1(3

)1(9

νν

−

⎟

⎠

⎞

⎜

⎝

⎛

−

(5)

The Young’s modulus was calculated from equation

(5) using Matlab software (MathWorks, USA).

Figure 3: Schematic representations of a membrane

deformed by micro-shaft poking (MSP) indentation.

Two theoretical models were used to examine the

relaxation behaviour of the hydrogels during

indentation. The 3-parameter standard linear model

and 5-parameter Maxwell-Weichert model were

both used to describe the viscoelastic relaxation

response under a constant strain (Figure 4).

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

212

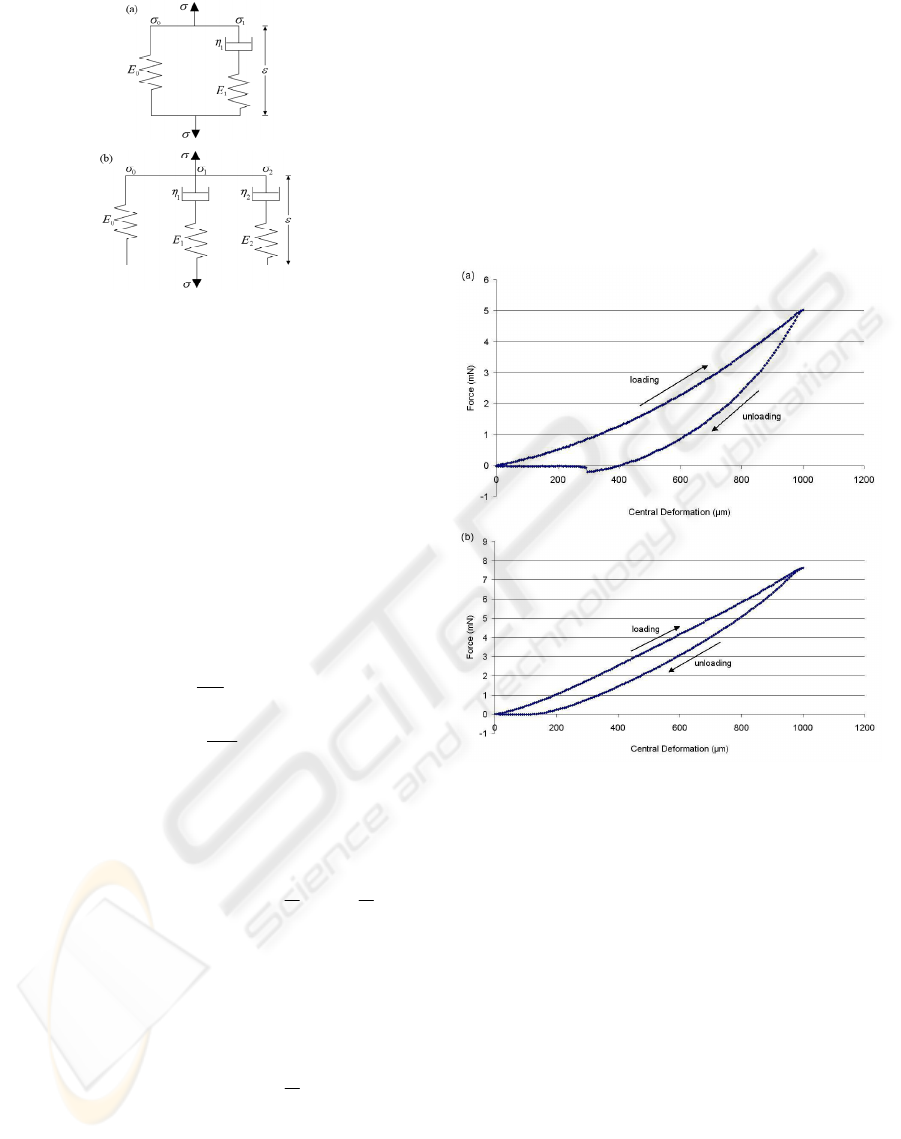
Figure 4: Schematic representation of the (a) 3-parameter

standard linear model and (b) 5-parameter Maxwell-

Weichert model.

For a 5-parameter Maxwell-Weichert model, which

consists of a single spring and two Maxwell

elements in parallel, the total stress, σ(t), equals to

the sum of the stresses applied to the spring and the

Maxwell elements;

210

)(

+=t (6)

where σ

is the stress applied to the spring and σ

and

are the stresses applied to each Maxwell element

and whose values can be described as;

(7)

εσ

−

(8)

εσ

−

= (9)

where η refers to the dashpot viscosity. By

substituting equations (7), (8) and (9) into equation

(6), the stress relaxation function g(t), which equates

to σ(t)/σ(0), can be described as;

210

)(

ττ

eAeAAtg

−−

++=

(10)

where A

, A

and A

represents the strain dependent

amplitudes, and τ

) & τ

) represent

strain dependent time constants.

For the standard linear model, the stress relaxation

function is written as;

)(

eAAtg

−

(11)

The values for A and τ were determined using non-

linear regression analysis for both relaxation models.

4 RESULTS AND DISCUSSIONS

4.1 Young’s Moduli of Hydrogels

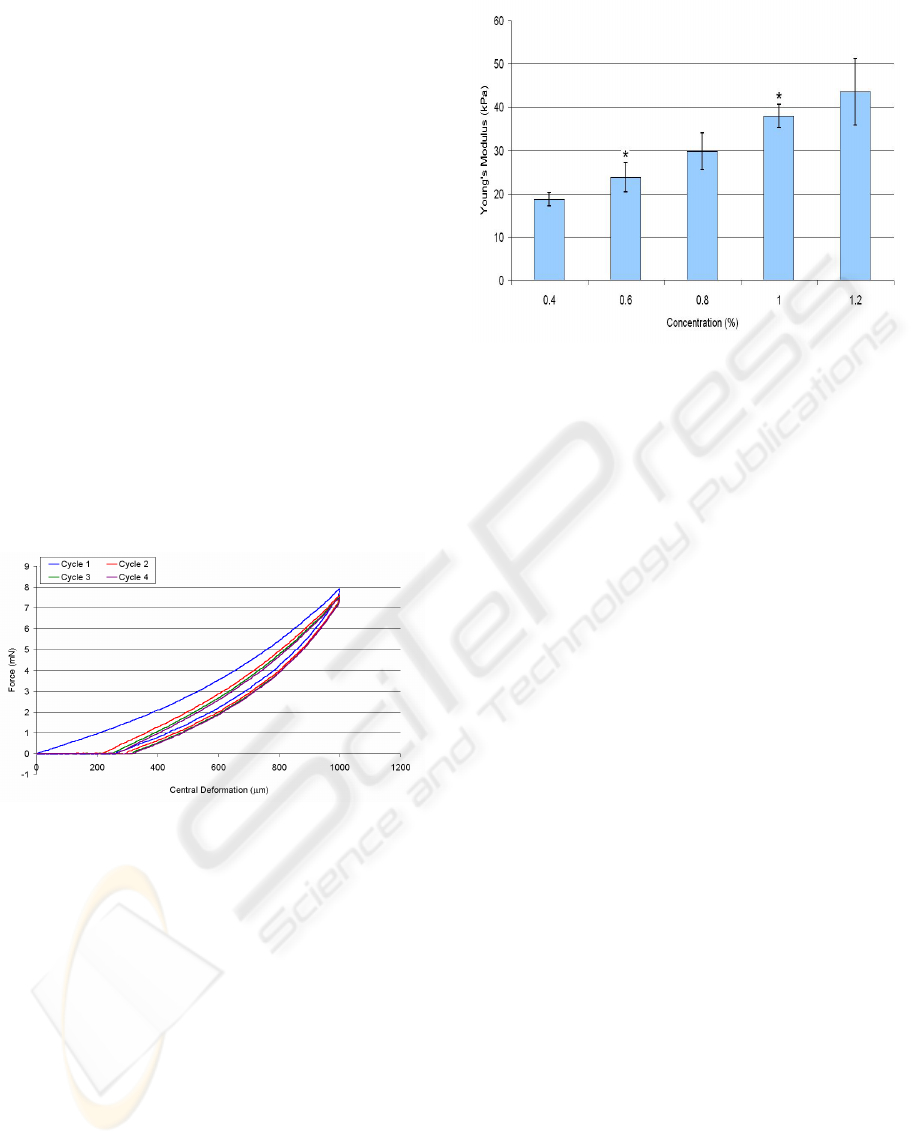
A typical force-displacement curve for a 2% w/v

alginate and 2% w/v agarose hydrogel indented to

1000µm are shown (Figure 5 (a) & (b)). It can be

seen that the loading and unloading curves did not

match. This type of behaviour, referred as

hysteresis, is common in viscoelastic materials and

is the result of energy dissipation during loading.

Figure 5: The MSP-measured loading-unloading curves

of a hydrogel membrane with (a) 2% alginate & (b) 2%

agarose.

The loading-unloading curves appear less linear for

alginate hydrogel than agarose hydrogels and there

was a more significant difference between the

loading and unloading curves for alginate. This

suggests that alginate has non-linear viscoelastic

characteristics while agarose has more linear elastic

characteristics. This type of mechanical behaviour

agrees with the findings from previous publications

(Bonn et al., 1998; Zhang et al., 2005). It was also

found for some of the alginate hydrogels that the

indentation force became negative for a short period

during unloading. This can be explained by

adhesion forces between the indenter and the

hydrogel causing the indenter to adhere onto the

hydrogel while unloading (Gupta et al., 2007).

Several loading and unloading cycles were

recorded for individual hydrogels. It was noticeable

MICRO-SHAFT-POKING - A Novel Instrument for Mechanically Characterizing Soft Biomimetic Membrance

213

that different indentation cycles on the same

hydrogel did not match although later indentation

cycles appeared to match much more closely than

earlier cycles. It can be seen (Figure 6) that for a 2%

alginate hydrogel, after the first indentation cycle an

increase in force was only detected after the indenter

has been lowered by over 200 μm. This would

suggest that plastic deformation of the alginate

hydrogels had occurred in addition to elastic and

viscoelastic deformation. The plastic deformation,

in addition to the viscous properties of the hydrogel,

prevented the hydrogel from fully returning to its

original pre-indentation shape. There was also a

small decrease in the amount of force required to

indent the hydrogel with each cycle. This decrease

in force was reduced with each cycle until reaching

there was no functional force decrease was

detectable. This phenomenon is common in

biological materials (Fung, 1993) and is the

combination of fibre reorganization and fluid

movement within the tissue. The loading-unloading

cycles for agarose appeared to match more closely

than for alginate.

Figure 6: The MSP-measured loading-unloading cycles for

a 2% alginate hydrogel.

The Young’s moduli of agarose hydrogels of

different concentrations indented up to 1000 μm are

displayed (Figure 7). Agarose was preferred to

alginate for calculating the Young’s modulus since it

had a more linear elastic response to indentation.

The Young’s modulus of alginate hydrogels varies

in literature with a range between 1 kPa and 100 kPa

(Awad et al., 2004; Drury et al., 2004). A non-linear

loading curve would result in the values for Young’s

modulus becoming dependent on the indentation

depth. It can be seen that there was an almost linear

increase in Young’s modulus with agarose

concentration. Simple regression analysis was used

to confirm the linearity of Young’s modulus with

agarose concentration between 0.4−1.2% with a

coefficient of determination (R²) equal to 0.9935.

Figure 7: Young’s modulus of agarose hydrogels

measured by the MSP indentation (± standard deviation,

n=4). *represents a significant difference with a 95%

confidence over the previous concentration determined

using ANOVA-tukey test.

The standard deviation bars show a high degree of

repeatability in measuring different agarose hydrogel

with the same concentration. Interestingly when the

same hydrogel was measured several times, the

standard deviation was further reduced i.e. for 0.5 %

agarose hydrogel indented to 1000 µm four times, E

= 20.9 ± 0.7 kPa. The values obtained for 1%

agarose by the MSP method appear resemble those

found by Bonn et al. (1998) using 3-point bending

and Nyland & Maughan (2000) using atomic force

microscopy.

4.2 Stress Relaxation of Hydrogels

Normalized force relaxation data was collected for

both agarose and alginate hydrogels. The hydrogels

were indented to a central displacement depth of

1000µm, which was maintained for 45 minutes. For

times longer than 45 minutes, dehydration of the

hydrogel would affect the measurement readings.

Both agarose and alginate appeared to exhibit

relaxation behaviour consistent with viscoelastic

materials (Figure 8 (a) & (b)). The amount of force

required to maintain the indentation displacement

was reduced over time. The normalized force

initially decreased quickly but then slowed until

reaching a plateau. Alginate appeared to

demonstrate a greater relaxation response than

agarose, which suggests it is more viscoelastic than

agarose, which has more elastic characteristics.

Nonlinear regression analysis, performed

using XLStat (Addinsoft, USA), was used to

determine the ability of the 3-parameter standard

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

214

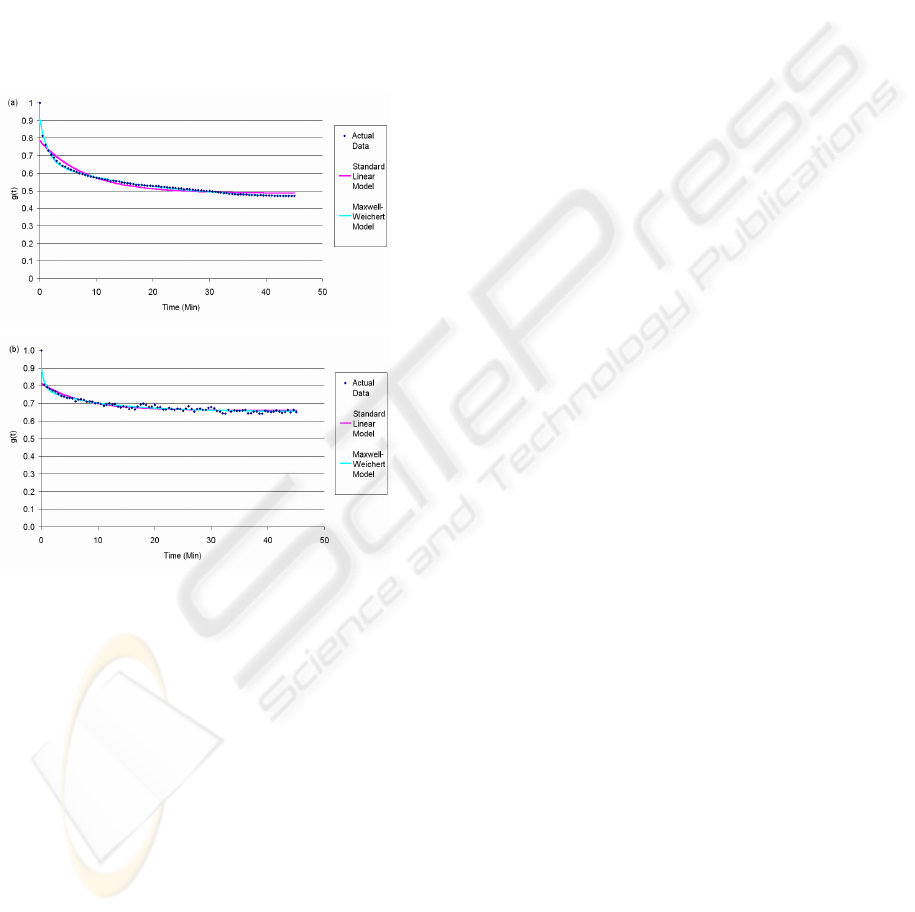
linear model and 5-parameter Maxwell-Weichert

model to describe the hydrogels’ relaxation

responses to the deformation applied by MSP. Both

models appear to show a high degree of correlation

between the actual data and the theoretical model

data (Figure 8). The values for coefficients of

determination (R²) for agarose and alginate

hydrogels were found to be greater than 0.9 using

the standard linear model and greater than 0.95 for

the Maxwell-Weichert model. This suggests that the

5-parameter Maxwell-Weichert model is capable of

providing a more accurate representation of the

relaxation response than the standard linear

model.

Figure 8: Actual and theoretical model normalised force

data for (a) a 2% alginate and (b) a 1% agarose hydrogel at

a constant indentation of 1000µm.

5 CONCLUSIONS

The MSP method has been applied to examine the

mechanical and viscoelastic characteristics of

various biomimetic materials, i.e., agarose and

alginate hydrogel membranes and their results have

been demonstrated to be satisfactory. Incorporated

with simple analyses, the new instrument has been

shown to be capable of determining quantitatively

viscoelastic and mechanical properties based on

experimental data of loading/unloading and stress

relaxation curves. The instrument has potentials for

testing other soft biological materials, such as

human and animal skins.

REFERENCES

Awad H. A., Quinn Wickham M., Leddy H. A., Gimble, J.

M., Guilak F. 2004, ‘Chondrogenic differentiation of

adipose-derived adult stem cells in agarose, alginate

and gelatin scaffolds’, Biomaterials, Vol. 25, no. 16,

pp. 3211-3222

Bonn D., Kellay H., Prochnow, M. Ben-Djemiaa K.,

Meunier J. 1998, ‘Delayed fracture of an

inhomogeneous soft solid’, Science, Vol. 280, no.

5361, pp. 265-267

Drury, J. L., Dennis, R. G. & Mooney, D. J. 2004, ‘The

tensile properties of alginate hydrogels’, Biomaterials,

Vol. 25, no. 16, pp. 3187-3199

Espinosa H. D., Prorok B. C., Fischer M. 2003, ‘A

methodology for determining mechanical properties of

freestanding thin films and MEMS materials’, J. of the

Mechanics and Physics of Solids, Vol. 51, no. 1, pp.

47-67

Fung, Y.C. 1993, Biomechanics: mechanical properties of

living tissues, Springer-Verlag, 2

edition, New York.

Gupta, S., Carrillo, F., Li, C., Pruitt, L., Puttlitz, C. 2007,

‘Adhesive forces significantly affect elastic modulus

determination of soft polymeric materials in

nanoindentation’, Materials Letters, Vol. 61, no. 2, pp

448-451

Johnson, K.L. 1985, Contact Mechanics, Cambridge

University Press, Cambridge

Liu K. K., Khoo, H. S., Tseng, F. G. 2004, ‘In situ

mechanical characterization of square microfabricated

elastomeric membranes using an improved

microindentation’, Review of Scientific Instruments,

Vol. 75, no. 2, pp. 524-531

Lu, S., Dikin, D. A., Zhang, S., Fisher, F. T. 2004,

‘Realization of nanoscale resolution with a

micromachined thermally actuated stage’, Review of

Scientific Instruments, Vol. 75, no. 6, pp. 2154-2162

Menciassi, A., Scalari, G., Eisinberg, A., Anticoli, C.,

Francabandiera, P., Carrozza, M. C., Dario, P. 2001,

‘An instrumented probe for mechanical

characterization of soft tissues’, Biomedical

Microdevices, Vol. 3, no. 2, pp. 149-156

Nyland, L. R., Maughan, D. W. 2000, ‘Morphology and

transverse stiffness of drosophila myofibrils measured

by atomic force microscopy’, Biophysical Journal,

Vol. 78, no. 3, pp 1490-1497

Ratner, B. D., Hoffman, A. S., Schoen, F. J., Lemons J. E.

1996, ‘An Introduction to Materials in Medicine’,

Academic Press, New York

Scott, O. N., Begley, M. R., Komaragiri, U., Mackin T. J.

2004, ‘Indentation of freestanding circular elastomer

films using spherical indenters’, Acta Materialia, Vol.

52, no. 16, pp. 4877-4885

Timoshenko S. P.,Woinowshy-Kreiger S. 1959, Theory of

plates and shells, McGraw-Hill, Singapore, 2

Edition

Zhang, J., Daubert, C. R., Foegeding, E. A. 2005,

‘Fracture analysis of alginate gels’, Journal of Food

Science E: Food Engineering and Physical Properties,

Vol. 70, no. 5, pp. 425-431

MICRO-SHAFT-POKING - A Novel Instrument for Mechanically Characterizing Soft Biomimetic Membrance

215