FPGA-BASED COMPUTATION OF THE INDUCTANCE OF

COILS USED FOR THE MAGNETIC STIMULATION OF THE

NERVOUS SYSTEM

Ionuţ Trestian, Octavian Creţ, Laura Creţ, Lucia Văcariu, Radu Tudoran

Computer Science and Electrotechnics Department, Technical University of Cluj-Napoca, Cluj-Napoca, Romania

Florent de Dinechin

LIP, Ecole Normale Supérieure de Lyon, UMR CNRS / INRIA / ENS-Lyon / Université Claude Bernard Lyon 1

Keywords: Magnetic stimulation, slinky coils, inductance computation, FPGA, floating point, VHDL

Abstract: In the last years the interest for magnetic stimulation of the human nervous tissue has increased

considerably, because this technique has proved its utility and applicability both as a diagnostic and as a

treatment instrument. Research in this domain is aimed at removing some of the disadvantages of the

technique: the lack of focalization of the stimulated region and the reduced efficiency of the energetic

transfer from the stimulating coil to the tissue. Better stimulation coils can solve these problems. Designing

coils is so far a trial-and error process, relying on very compute-intensive simulations. In software, such a

simulation has a very high running time. This paper proposes and demonstrates an FPGA-based hardware

implementation of this simulation, which reduces the computation time by 4 orders of magnitude. Thanks to

this powerful tool, some significant improvements in the design of the coils have already been obtained.

1 INTRODUCTION

The preoccupation for improving the quality of life,

for persons with different handicaps, led to extended

research in the area of functional stimulation. Due to

its advantages compared to electrical stimulation,

magnetic stimulation of the human nervous system

is now a common technique in modern medicine

(Mozek and Flak, 1999).

A difficulty of this technique is the need for

accurate focal stimulation. Another one is the low

efficiency of power transfer from the coil to the

tissue. To address these difficulties, coils with

special geometries must be designed.

This process requires testing a huge number of

geometries to find an adequate solution for the

desired application (Griškoval and Höppner, 2006).

One of the major problems that appear in the

design phase is the computation of the inductivity of

the stimulating coil. For simple shapes of the coils

(circular), one can determine analytical computation

formulas. When, however, the shape and the spatial

distribution of the coil’s turns do not belong to one

of the known structures, a numerical method needs

to be used for determining the inductivity.

The idea is to divide the coils in small portions.

Starting from this method, two computation systems

are presented in the paper:

• The first one is classical and it just consists of a

software implementation (Matlab);

• The second one consists of realizing a hardware

architecture that exploits the intrinsic parallelism

of the problem. The physical support of this

architecture is an FPGA device.

The problem with the software implementation is

its running time. Coils are designed by trial-and-

error, and this approach is impractical if each trial

requires half a day of computation. Besides, as this

time grows with the complexity of the coil, it

prevents designing complex coils. This paper shows

that FPGA-based hardware acceleration is able to

solve this bottleneck.

The simulation of magnetic stimulators with

complex forms requires dividing their coils in

several parts. The self-inductance of the circuit,

divided in n parts, can be computed with formula

151

Trestian I., Cre¸t O., Cre¸t L., V

acariu L., Tudoran R. and de Dinechin F. (2008).

FPGA-BASED COMPUTATION OF THE INDUCTANCE OF COILS USED FOR THE MAGNETIC STIMULATION OF THE NERVOUS SYSTEM.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 151-155

DOI: 10.5220/0001050301510155

 SciTePress

(1). This mainly adds up the self-inductivities of the

separate segments with the mutual inductivities of

all the involved segments. The method is well

described in (Creţ et. al., 2007); the operations

involved in computing the inductivity of a coil are:

logarithm, division, addition and multiplication.

()

kiforMLL

≠+=

∑∑∑

===

111

(1)

2 SOFTWARE

IMPLEMENTATION

A coil is made up of a certain number of turns rolled

around a central rod. Each turn can be considered as

a perfect circle. The coil is structured on several

vertical stages. On each stage there are more turns

(horizontal turns). The coils parameters are: the

radius, the diameter of the metallic turn and the

distance (insulation) between consecutive turns.

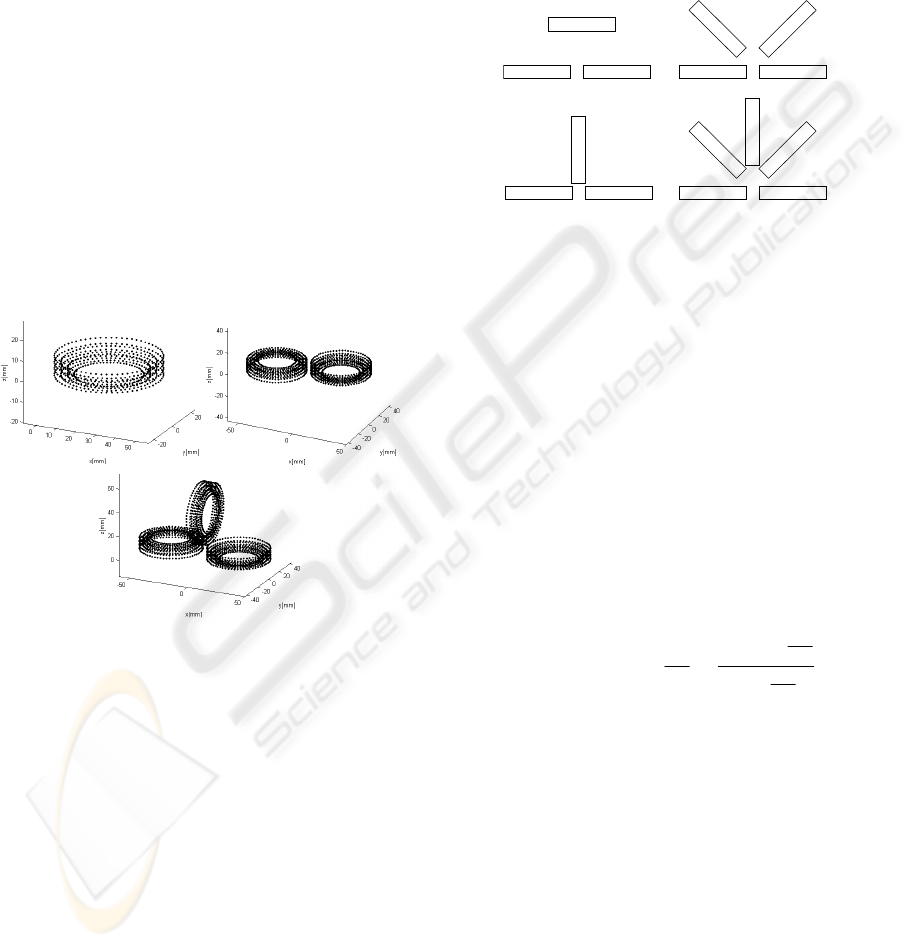
Figure 1: Coil approximation using a finite number of

points.

It is possible to have a different number of turns

on every vertical stage. It is also possible to have a

variable number of vertical stages, as shown in

Figure 1. A complete magnetic stimulation device

contains a Slinky coil. Considering a coil with N

turns, the “Slinky-k” coil is generated by spatially

locating these turns at successive angles of

()

1/180x −ki degrees, were i = 0, 1, …, k-1. If the

current passing through this coil is I, then the central

leg carries the total current N x I. These coils are

shown in Figure 2, where each rectangle represents a

leaf of the coil, viewed in perspective.

The turns are approximated by a finite number of

points. We considered, after a series of tests, that a

suitable amount of points on a turn is 64.

We have to take each of the 64 points and

combine them into segments made up of one point

and the consecutive one. After this, each segment is

held as a reference. Then, formula (1) is applied

using this reference segment and all the other

segments on the coil. For each pair of segments a

value is obtained. These values must be added in

order to obtain the coil’s total inductance.

Slinky_1

Slinky_2

Slinky_3

Slinky_4

Slinky_5

Figure 2: Magnetic coil structures of the stimulation

device.

There are two phases in the functioning of the

software implementation:

• In Phase 1, the coordinates of the points are

generated. These are computed using

trigonometric functions. The results

produced in this phase are also used in the

hardware implementation.

• In Phase 2, the actual computation of the

values is performed. Finally, we

accumulate the values corresponding to the

mutual and self inductivities.

The accumulation value includes some

intermediate values (var1 to 5) according to (Creţ et.

al., 2007):

var

varvar

log

var

rAccumulato rAccumulato

−

−+

⋅+=

(2)

The software implementation’s main drawback

is the extremely high running time, which can be in

the order of tens of minutes even for simple

configurations. For complex geometries of the coils,

it can exceed several hours (for instance, for a 58-

turns coil, about 5 hours run time on a recent PC).

3 HARDWARE

IMPLEMENTATION

3.1 FPLibrary

A Field-Programmable Gate Array (FPGA) is a

semiconductor device containing programmable

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

152

logic components (“logic blocks”), and interconnect.

Logic blocks can be programmed to perform simple

or more complex functions. In most FPGAs, the

logic blocks also include memory elements, from

flip-flops to more complete blocks of memories.

The hierarchy of programmable interconnects

allows logic blocks to be interconnected as needed

by the system designer, somewhat like a one-chip

programmable breadboard. Logic blocks and

interconnects can be programmed by the

customer/designer, after the FPGA is manufactured,

to implement any logical function (Guell et. al.,

2007).

Several libraries of floating-point operators for

FPGAs have been published. In this work, we use

FPLibrary, developed at Ecole Normale Supérieure

de Lyon (Detrey and De Dinechin, 2005) and freely

downloadable (Detrey and De Dinechin, 2007).

Mantissa size and exponent size parameterize each

operator in FPLibrary, allowing one to choose the

precision and the dynamic range of the numbers. It

provides operators for addition, subtraction,

multiplication, division and square root, some useful

conversions and some elementary functions

(currently exponential, logarithm and sine/cosine). It

is written in portable VHDL (Collange et al., 2006).

3.2 System Architecture

The hardware implementation implies the same two

phases as the software one, but Phase 1 is not

computation-intensive and its implementation is kept

in software.

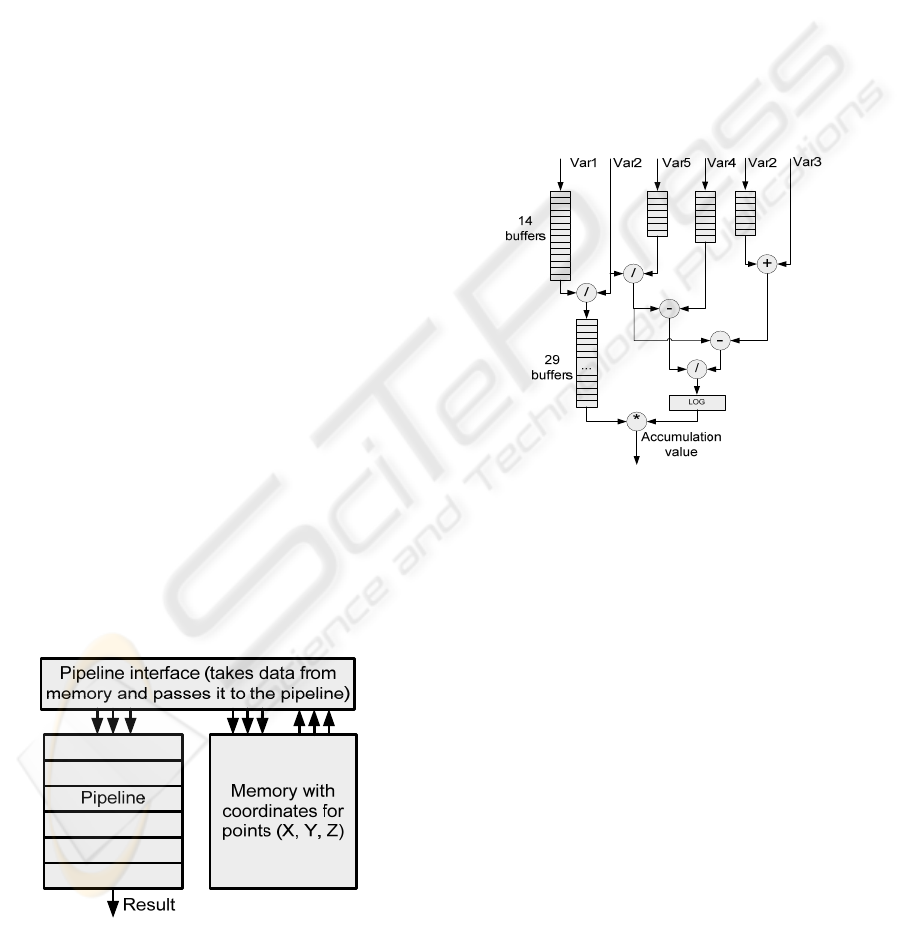
In the Figure 3 below a block diagram of the

system is displayed. Three main blocks can be

distinguished. The most important block is the

pipeline stage, which receives values, computes

them, and in a final stage accumulates them.

Figure 3: Architecture of the hardware system.

The coordinates are stored in a Block RAM

memory. There are 3 memories, one for each

coordinate, X, Y, and Z. The synchronization logic,

which gives the data to the pipeline, is implemented

in a special interface. This interface consists of

counters and latches. The counters are orchestrated

to generate the proper addresses, while the latches

are needed to implement a caching logic, which

saves some of the memory used.

The design of the Accumulator is the most

important part of the pipeline’s architecture, since it

computes intermediary values and at the end

provides the final result. As mentioned above,

special considerations need to be made with regard

to the accumulator because of the latencies

introduced by the adders in the FPlibrary (3 cycles).

Figure 4: Second stage. Computing accumulation value.

The values that will be accumulated come and

enter the final stage, which is an accumulator having

a classical structure, using a feedback input.

3.3 Hardware Implementation Issues

The performance and feasibility of the hardware

implementation largely depends on its physical

support. Our hardware platform was a Digilent Inc.

board populated with a Xilinx Virtex2PRO30 FPGA

device. The problem with this implementation was

that it is quite large: it depleted the space of the

FPGA device we had available at this moment. To

estimate the total space needed, we synthesized the

design for a larger FPGA device (a Virtex4 160LX).

A report of the device utilization is shown below:

Selected Device: 4vlx160ff1148-12

Number of Slices: 23656 out of 67584 35%

Number of Slice Flip Flops: 20834 out of 135168 15%

Number of 4 input LUTs: 44515 out of 135168 32%

Maximum frequency: 137.552 MHz.

FPGA-BASED COMPUTATION OF THE INDUCTANCE OF COILS USED FOR THE MAGNETIC STIMULATION

OF THE NERVOUS SYSTEM

153

The implementation fits without problems on

this Virtex4 board. Regarding an implementation on

our Virtex2Pro board two options were available.

The first option was to reduce the precision at

which the pipeline operated. This ensured a

reduction of both the buffer stages that provided the

synchronization between the stages and a reduction

in size of the operators.

This option was first implemented. We reduced

the mantissa of the operands by 10 bits. Instead of a

large mantissa having 23 bits, the mantissa now had

only 13 bits. Although the design fitted on a Virtex-

II Pro board at about 98% of its capacity, the results

obtained with this method were discouraging. They

were more then 30% off from the actual result

provided by Matlab. Therefore another method

needed to be found.

The next option was to reduce the frequency at

which the pipeline stage operates and time-multiplex

some of the resources (square root – three

occurrences in design, some of the adders). This has

the advantage of preserving the pipeline’s precision,

the cost being a reduction in speed: the operating

frequency was 85.714, MHz related to the weaker

characteristics of the FPGA device and the more

precise timing requirements.

4 EXPERIMENTAL RESULTS

The main achievement of the hardware

implementation over the software one is the

reduction in computation time. By performing one

accumulation per clock cycle the hardware solution

is indeed efficient and can be used even for the most

complex magnetic stimulation systems.

In terms of complexity, both implementations, in

software and in hardware, have the same

complexity, O(n

) with n being the number of

distinct segments. As mentioned in Section 4, the

specific hardware structure performs one

accumulation per clock cycle. That means that each

clock cycle, a mutual inductivity between two

segments is evaluated. The software implementation

performs the same computations in a longer time.

We have analyzed our software and hardware

implementations using the Slinky_1, Slinky_2 and

Slinky_3 configurations (Figure 2). The values are

given in Table 1, where a comparison is shown

between the results provided by the software and the

hardware solutions.

First we analyze simpler cases, 1 to 4 turns. The

outer turns are the widest turns on the coil, while the

inner ones are the neighbors of the outer turns

located closer to the center. Then, the results for

these configurations are presented. The analyzed

quantity was the inductivity. The number of

segments represents an indicator of the complexity.

The results of the two methods analyzed for the

three configurations mentioned always stayed in the

range of 3-4% of each other, with the Matlab results

being slightly bigger than the results given by the

hardware implementation. This can be attributed to

the fact that Matlab uses by default double precision

while in our system we have used only single

precision operations. Indeed, a rough worst-case

error analysis tells us that the accumulation, in the

largest coil test, of 10.1920² floating-point numbers

introduces a cumulative rounding error that may

invalidate up to log

(10.1920²) = 25 bits of the

result, when the mantissa of a single-precision

number holds 24 bits only.

This is a worst-case situation: in an actual

simulation, the rounding errors compensate each

other – this is why our results are still accurate.

However, it shows that we will require increasing

the precision of the floating-point format to use this

architecture on larger coils. Fortunately, this extra

precision is mostly useful in the final accumulator.

Table 1: Comparison of results.

Configuration Inductivity

(Hardware)

[μH]

Inductivity

(Software)

[μH]

Number

segments

1 outer turn 0.097 0.097 64

2 outer turns 0.30 0.30 128

4 turns (2 out. 2

in.)

0.92 0.93 256

Slinky_1 coil 3.81 3.9 640

Slinky_2 coil 8.4 8.6 1,280

Slinky_3 coil 13.32 13.6 1,920

The flexibility of FPGAs allows us to use

different precisions in different parts of the

architecture. Besides, a format intermediate between

single and double precision may be used. For us, a

32- or 36-bit mantissa would already be overkill

(double-precision has a 53-bits mantissa). We will

test this as soon as we get hold of a board with a

larger FPGA than the Virtex-II used here. It should

be noted that this more accurate pipeline will require

more hardware, but the same execution time: it will

still compute one accumulation per cycle.

One can see from Table 2 that the software

running time is very large, so software computation

becomes prohibitive for large systems.

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

154

Table 2: Comparison of performance.

Configuration Duration

(hardware)

[no. of

clock

cycles]

Running

speed*

(hardware)

[seconds]

Running

speed

(software)

[seconds]

1 outer turn 40,960 0.0004

4.2

2 outer turns 163,84

0.0019

4 turns

(2 out. 2 in.)

655,36

0.0076

Slinky_1 coil 4,096,

000

0.0470

420

Slinky_2 coil 16,384

,000

0.1941

1,680

Slinky_3 coil 36,864

,000

0.4294

3,600

* at 85.714 MHz, clock period 11.66 ns

As a global comparison, the hardware solution

runs approximately four orders of magnitude faster

then the software one. The frequency is related to

the physical board we had available, but for a more

recent FPGA chip (i.e. Virtex4LX160, for which we

did some simulations, or Virtex5), the device’s

capacity as well as the working frequency will

increase, thus leading to an improved performance.

5 CONCLUSIONS AND FUTURE

WORK

An adequate geometry of the stimulation coil can

lead to a better focality of the stimulus (the ability of

a coil to stimulate a small area of the tissue) and it

can also improve the efficiency of the energy

transfer from the coil to the target tissue. The form

and size of the turns, their position inside the coil,

the insulation gap between turns are all important

parameters that should be considered when

designing a magnetic coil. Therefore, in order to

establish the most suitable coil geometry for a

specific medical application, a large number of

structures have to be tested, making of coil design a

trial-and-error process, even if the risk involved is

only computation time.

In (Creţ et. al., 2007), we analyzed the influence

that space distribution of the magnetic coils’ turns

has on the efficiency of energy transfer from the

stimulator to the target tissue. The analysis was

performed for a Slinky_3 coil configuration, with

applications on transcranial magnetic stimulation

(TMS). It turned out that the electrical energy

dissipated in the circuit of the stimulator – required

in order to achieve the activation threshold – is 25%

lower for the most efficient configuration than for

the less efficient one, and the coil heating per pulse

is also 35% smaller!

This estimation was based on the inductivity

calculus described in this paper, and the large

number of analyzed structures required a less time-

consuming computation technique, the hardware

implementation described above.

Since every medical application requires its own

optimal structure of the magnetic coil, the results

emphasized in this paper can play an important role

for future work on coil design.

Because of the large amount of operations

involved (several tens of millions just for one coil) it

is very hard to debug such a hardware system at

least at an acceptable level, but the obtained results

show an excellent concordance with those obtained

in software. Our implementation has the advantage

of greatly speeding up the computation time and

hence shortening the design process. On larger

FPGA devices the process can achieve a greater

speed by accommodating more computational

structures in parallel. These structures would

evaluate multiple pairs of segments in parallel and

accumulate them to the final value.

REFERENCES

Collange, S., Detrey, J., & De Dinechin, F. (2006).

Floating Point or LNS: Choosing the Right Arithmetic

on an Application Basis. In Proceedings of the 9

EUROMICRO Conference on Digital System Design,

Dubrovnik, Croatia, 197-203.

Creţ, L., Pleşa, M, Micu, D.D., & Ciupa, R. (2007).

Magnetic Coils Design for Focal Stimulation of the

Nervous System. In Proceedings of EUROCON 2007,

IEEE International Conference on Computer as a

Tool, Warsaw, Poland, 1998-2003.

Detrey, J, & De Dinechin, F. (2005). A Parameterizable

Floating-Point Logarithm Operator for FPGAs. In

Proceedings of the 39

Asilomar Conference on

Signals, Systems & Computers, 1186 – 1190.

Detrey, J, & De Dinechin, F. (2007). FPLibrary.

https://lipforge.ens-lyon.fr/projects/fplibrary/.

Griškova1, I., & Höppner, J. (2006). Transcranial

magnetic stimulation: the method and application.

Medicina (Kaunas), 42(10), 792-804.

Guell, D., El-Ghazawi, T., Gaj, K., & Kindratenko, V.

(2007). High-Performance Reconfigurable Computing,

IEEE Computer, 40 (3), 23-27.

Mozeg, D., & Flak, E. (1999). An Introduction to

Transcranial Magnetic Stimulation and Its Use in the

Investigation and Treatment of Depression. University

of Toronto Medical Journal, 76 (3), 158-162.

FPGA-BASED COMPUTATION OF THE INDUCTANCE OF COILS USED FOR THE MAGNETIC STIMULATION

OF THE NERVOUS SYSTEM

155