A SIMPLE DEVICE TO MEASURE GAZE ANGLES IN VISUAL

TASK ANALYSES

A. Page, B. Mateo, J. Garrido-Jaén, R. Marzo

Instituto de Biomecánica de Valencia, Universidad Politécnica de Valencia, Camino de Vera s/n, 46022 Valencia, Spain

J. C. Dürsteler, A. Giménez, C. Prieto

Indústrias de Óptica, S.A. (INDO). Alcalde Barnils, 72. 08174 Sant Cugat del Vallès, Barcelona, Spain

Keywords: Optometry, Visual strategy, Head Movements, Eye tracking, Progressive Addition Lenses.

Abstract: This paper presents a simple device to measure visual maps and head motion to analyze the visual strategy

in optometric applications. Instead of using the common approach of conventional eye trackers based on

continuous pupil–corneal reflection detection, a simple method based on photogrammetry is proposed. This

method only measures the head movements, the gaze direction and the visual map can be calculated on the

hypothesis that subjects’ gaze follows a known visual stimulus accurately.

In order to validate this hypothesis, an experiment has been carried out to calculate the subject’s accuracy

when tracking the stimulus. The gaze direction was measured both with conventional eye tracking and with

the proposed technique and the measured gaze angles were compared. The results show that the subjects

effectively follow the stimulus during the task and thus the main hypothesis of the proposed system is

confirmed. Therefore, the analysis of head movement can supply an indirect estimation of the visual angles

that is as accurate as the measures obtained with more complex devices.

1 INTRODUCTION

Visual strategy can be defined as the coordination of

eyes and head movements in order to perform a

visual task. The study of visual strategy has received

some interest from fields as diverse as neuroscience

and psychophysics, customer behaviour analysis and

advertising, ergonomics, sports or lenses design and

optometry.

Techniques of eye-tracking have been used for a

long time in the fields of psychophysics and

neuroscience. Richardson and Spivey have

published a complete survey about the main research

areas in these fields (Richardson and Spivey, 2004

;

Richardson and Spivey, 2004

). The analysis of

visual strategies can also provide information about

the consumer behaviour and thus help to identify

factors that determine the attention allocated to

different advertisements (Treistman and Gregg,

1979; Lohse, 1997).

In the ergonomics scope, research on visual

strategy is mainly focused on the study of the visual

demands of different tasks in order to improve the

workplace design and task performance (Engström

et al. 2005). Other applications are related to the

design of technical aids for disabled people, such as

control systems based on eye-gaze tracking (Sesin et

al. 2003). The visual strategy is particularly

important in the study of some complex tasks in

sports such as ball sports or boxing, in which a

player needs to determine the future trajectory of the

ball (or hand). Thus, several studies have been

carried out to analyze the influence of visual strategy

on the subject skills (Ripoll et al. 1995; Land and

McLeod, 2000).

The use of eye movement analysis in the field of

optometry is more recent and its applications seem

promising. Monitoring visual performance can help

to quantify the state of the ocular motor system and

provide valuable diagnosis and management support

(Abadi, 2006). Besides, visual strategies analyses are

the basis of some aspects of corrective lenses design,

especially to assess the comfort of progressive

addition lenses (PALs) wearers. Some studies in this

field have been performed to understand the

differences of users’ behaviour when using different

119

Page A., Mateo B., Garrido-Jaén J., Marzo R., C. Dürsteler J., Prieto C. and Giménez A. (2008).

A SIMPLE DEVICE TO MEASURE GAZE ANGLES IN VISUAL TASK ANALYSES.

In Proceedings of the First International Conference on Biomedical Electronics and Devices, pages 119-125

DOI: 10.5220/0001046501190125

 SciTePress

PAL designs or single vision lenses (Selenow et al.

2002; Han et al. 2003; Hutchings et al. 2007).

Several techniques have been used for measuring

eye movement as well as for characterizing visual

strategies. Morimoto and Mimica (Morimoto and

Mimica, 2005) present a good survey of techniques

for eyes gaze tracking. The most widely used are

based on the automatic detection of the pupil-corneal

reflection. The eye is illuminated by a distant, low-

power, infra-red light source, and this creates an

image that is seen as a highlight spot on the surface

of the cornea. The image is analysed by a computer,

which calculates the centre of the corneal reflection

as well as the centre of the pupil. The distance from

the pupil centre to the corneal reflection is

proportional to eye rotation, and thereby provides an

estimation of the gaze direction. Since the eye

position varies as the head moves, the head should

remain still during the measurement; otherwise the

movement of the head must be measured in order to

transform the relative direction of gaze into absolute

directions to the visual targets.

Then, a complete description of visual strategy

needs both gaze direction and head position analysis.

Head motion can be accurately measured in real-

time by means of a magnetic location system

(Hutchings et al. 2007), although these systems are

intrusive because a device must be placed on the

subject head. There have been some recent attempts

to avoid such kind of devices by measuring head

movements by means of a 3D face tracking analysis,

as proposed in (Beymer and Flickner, 2003).

The systems based on pupil-corneal reflection

need some type of calibration to transform the input

data (reflections’ locations) into absolute gaze

directions. A typical calibration procedure presents

the user a set of visual targets that the user has to

look at while the corresponding measurement is

taken. From these measurements a map of

correspondences or calibration function can be

obtained. Although several models to calibrate the

eye tracker systems have been developed, the

calibration process is one of the worst problems in

current commercial systems. On the one hand, the

calibration functions are very sensitive to head

motion, which is the cause of the main source of

inaccuracy. On the other hand, calibration is a

troublesome process that demands controlled

environmental conditions. For these reasons some

tracking systems are difficult to use and inadequate

for applications outside a research laboratory

(Schnipke and Todd, 2000).

A strategy to improve the accuracy and

simplicity of the systems is to adapt them to specific

functions, so that only the precise information is

measured in the simplest way. For example, some

clinical and optometric applications are focused on

the ocular motor performance when the subject

performs a specific task with well-known stimuli

(Abadi, 2006). This way, the measurement of the

absolute gaze direction is unnecessary and the

measurement of head movements and relative eyes

motion is enough.

The objective of this paper is to describe and

validate a new device to measure the relative motion

of eyes with the aim of obtaining visual maps. This

information could be useful to analyze differences of

visual strategies in the design of progressive addition

lenses. The device uses video-photogrammetry

techniques and it is based on the assumption that

only head motion measurement is necessary to

estimate eye gaze direction when the target position

is known.

In order to validate this proposed technique, an

experimental study has been performed in which the

subject accuracy when tracking a visual stimulus is

calculated. The measures obtained with our device

were compared with those a conventional eye

tracker. The results show that the measurement of

head movement can supply an indirect estimation of

the visual angles when the tracked target locations

are known and the results are as accurate as the

measures obtained with more complex devices.

2 MATERIALS AND METHODS

2.1 General Description of the

Equipment

The principle of operation of the proposed technique

assumes that a subject can effectively gaze at a

mobile target, so that eye gaze direction in relation

to the head is determined by knowing both target

and head positions, as well as the relative location of

eyes with respect to head.

The measurement system consists of a 650 x 500

mm dark screen, which shows a 1 cm illuminated

spot that moves along a continuous trajectory. At

both sides of the screen, two synchronised video

cameras record the subject’s head motion. Cameras

have a 640 X 480-pixel resolution with a 25 fps

recording speed. The cameras are equipped with

infrared filtersCameras have been previously

calibrated using the DLT algorithm (Abdel-Aziz and

Karara, 1971) and lenses distortion corrected by

means of the procedure described in (Ahmed and

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

120

Farag, 2005). Therefore, it is possible to accurately

measure head position and motion. This analysis can

be made from the coordinates of some face

distinctive points, using well-known image analysis

protocols as the Harris corner detector (Hartley,

2004). However, in order to simplify the

computations and to allow a real-time analysis, no

computational expensive image processing has been

used. Thus, the position and motion of head are

measured by means of a set of active makers. The

markers cluster consists of four infrared leds placed

on a diadem that adjusts at the head.

Besides, the system has an infrared light source

placed in the middle of the screen to create a corneal

reflection that allows detecting eyes’ position during

the calibration step.

2.2 Measurement Process

The measurement process is performed in two steps:

first the measurement of an initial reference position,

and then the measurement phase, where visual angle

is recorded during the performance of a tracking

visual task. In the first step, the subject sits 50 cm in

front of the screen. He is asked to adopt a neutral

head posture with the gaze direction approximately

horizontal. This position is considered as the

reference posture. Then measurement system detects

the markers’ positions and places the target in the

middle of the screen at approximately the eyes

height. Eyes positions are detected by the corneal

reflection produced by infrared light source. The

corneal reflection 3D position is automatically

measured. Thus, eyes centre position is calculated

assuming a spherical shape of the cornea with

known radius.

Simultaneously, markers’ positions are

determined and a local reference system linked to

the subject’s face is defined. The X axis is traced

from left to right eyes. The local coordinate’s origin

O is placed in the middle point between the eyes.

The Z axis is the most vertical axis belonging to the

plane perpendicular to X axis which pass throughout

O. Finally, the Y axis is defined to make the

reference system right-handed.

Therefore, right eye coordinates in the local

system are [d/2, 0, 0], where d is the subject’s

interpupilar distance.

Detection of corneal reflection is necessary only

at the first step. Once eyes relative positions with

respect to the diadem are identified, their position in

space can be determined from the head motion, and

no more check up is necessary. This fact avoids

having to perform high computational cost image

processing tasks and allows free head movements.

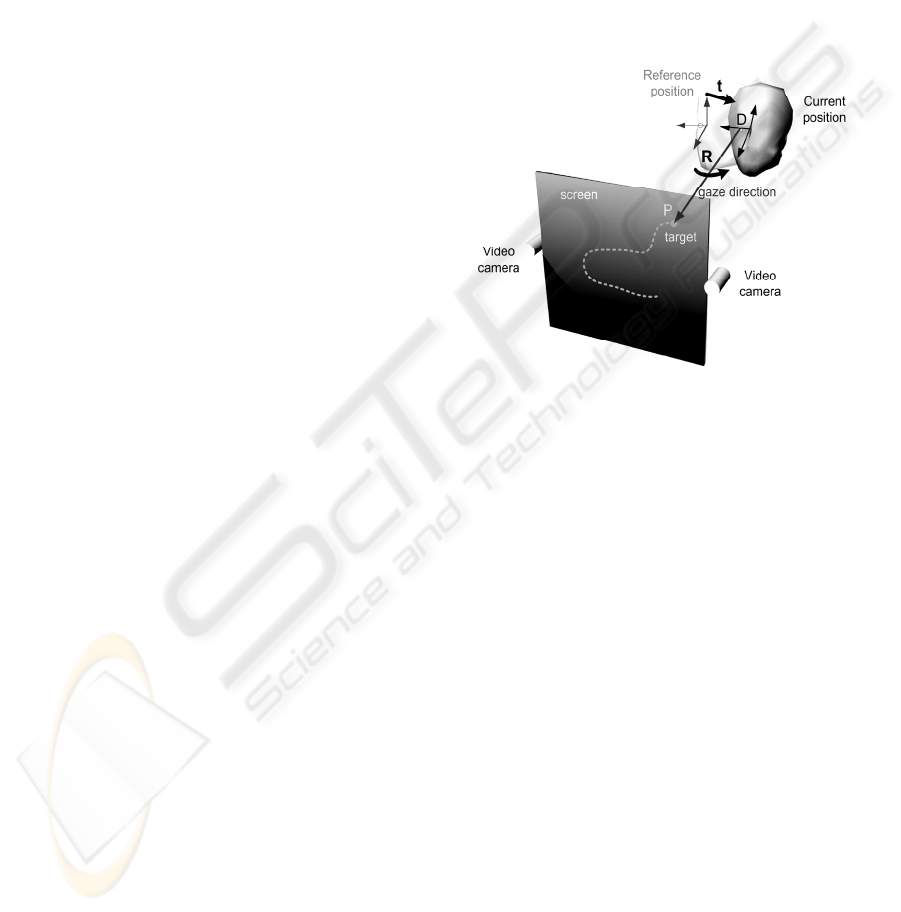
Figure 1 shows the equipment operating scheme

during a tracking test of a moving target. At each

instant, the target is located on the screen at a known

position, P. The subject has moved his head from the

reference position to a different one. This movement

is defined by translation t of the local reference

system and by the rotation matrix R in relation to the

initial reference position. Using t and R, the eyes’

current positions are determined. Specifically, right

eye will be placed at point D.

Figure 1: Equipment operating scheme.The subject looks

at a mobile target P on the screen. Head position and

motion are measured by means of two synchronized

videocameras. Gaze direction is estimated from head

position, location of P and the relative position of eyes in

the head.

alculation of head position and movement is

performed in real time from the diadem’s markers’

coordinates by using the algorithm described in

(Woltring et al., 1994). This algorithm allows

obtaining rotation matrix R and translation vector

tAssuming that a person tracks the target, actual

gaze direction is given by vector DP (Figure 1)

which can be calculated in the absolute reference

system. If this vector is expressed in the local

reference system, then the horizontal angle is

calculated as the angle that forms the DP projection

on the Z=0 plane with the local axis Y, whereas the

vertical angle is the one formed by DP line with the

Z=0 plane.

2.3 Equipment Accuracy Random

Instrumental Errors

The measurement of vision angles has two main

sources of error. First, the instrumental errors

A SIMPLE DEVICE TO MEASURE GAZE ANGLES IN VISUAL TASK ANALYSES

121

associated to 3D reconstruction process and head

movement measurement. Second, the error due to

the subject’s gaze deviation when tracking the

target. The latter error is studied in the experiment

described below, so this section focuses on

instrumental accuracy only.

Measurement errors of the markers’ coordinates

depend on camera resolution, accuracy of the marker

centroid determination, and separation between the

cameras (Hartley, 2004). In our system, focal

distance is close to 1000 pixels, measurement

centroids accuracy is estimated to be 0.3 pixel and

photogrammetric system baseline is b = 650 mm.

This configuration provides instrumental

coordinates’ error of around 0.1 mm in X and Z

coordinates and close to 0.2 mm in Y direction.

Angular and position errors associated to this

coordinates’ error estimation can be calculated by

means of the procedure described in (Page et al.,

2006). For the diadem geometry (four markers in a

15 x 15 cm squared), these errors are about 0.1º.

Linear displacement error is less than 0.1 mm. The

worst accuracy appears in the location of the eyes

centres, where a well-known corneal radius is

assumed. Then, an error of around 1 mm can be

expected. Nevertheless, this error has little effect on

the gaze angle estimation, because of the great

distance between subject and screen. So, if this

distance is 500 mm, the systematic angle error is less

than 0.1º for a gaze angle of 20º. Note that a correct

estimation of corneal radius is critical in

conventional tracking systems, because angle

direction computation depends upon this measure.

In summary, random instrumental errors

associated to photogrammetic techniques are really

small and they are negligible in relation with subject

performance errors due to the subject’s gaze

deviation when tracking the target. This source of

error is studied at the following section.

3 VALIDATION

The device operates on the hypothesis that subjects’

gaze follows the target accurately. Consequently, it

is possible to calculate the relative gaze direction

from the target location and the head movements.

Therefore, the validation consisted on evaluating the

subject’s gaze deviation from the target in a tracking

visual task. In order to do it, the measures obtained

with the proposed devices were compared with the

ones provided by a commercial eye tracker.

Two visual tasks were performed. The first had

to aim to estimate the accuracy of the conventional

eye tracker. The second consisted on a dynamic task,

tracking a moving target, with the aim to quantify

the deviation of gaze direction with respect to the

actual target location.

Five subjects participated in these experiments.

3.1 Equipment

Eye and head movements were recorded during the

tasks using a head mounted eye-tracker (Model 501,

ASL Applied Science Laboratories) integrated with

a head-tracker, 3SPACE FASTRAK (Polhemus,

Colchester, VT 05446, USA).

The eye-tracker measures the angle of gaze with

respect to a calibrated scene in the horizontal and

vertical directions. The accuracy reported in the

equipment specifications is less than 1 degree and

may increase to 2 degrees in the periphery of the

visual field.

3.2 Experimental Procedure

The visual tasks were displayed on a 19 inches

computer screen. Subjects sat in front of the screen.

The distance between monitor and subjects was 50

cm. The monitor height varied depending on the

subject to obtain a zero vertical gaze angle when

looking at the centre of the screen, point 5 in the

calibration scene (Figure 2).

Figure 2: Calibration Scene.

Previous to performing the tasks a calibration

process was completed for each user. This

calibration consisted on looking at 17 target points

located at known positions. During this process the

eye tracker records the corneal reflection of the left

eye as well as the pupil and head movements.

Once the calibration was carried out, the subjects

performed two visual tasks. In the first task (static

task) the subjects looked consecutively at each one

to 17 target points of the calibration scene during

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

122

three seconds while the eye and head position were

registered.In the second task (tracking task) subjects

were asked to follow with their eyes a moving target

onto the 19’’ black screen. The target was a red spot

moving with a pseudo-random trajectory on the

screen during two minutes. The trajectory consisted

on a set of concentric circles and radial lines from

the centre of the screen with a randomized sequence

(see figure 3). The velocity of the point motion was

7 cm/sec (8º/sec gaze angle, approximately). This

velocity is similar to the one used to measure the

visual maps.

4 RESULTS

The data registered in the static task was used to

estimate the accuracy of the eye tracker system as

the deviation between the gaze lines and the

measured ones by means the eye-tracker.

For each subject, the accuracy of the eye tracker

system was quantified as the standard deviation in

degrees of the horizontal and vertical eye angle

differences between actual and measures lines while

performing this static task (Table 1)

Results show that the standard deviations of

errors are smaller than 1º in all subjects for

horizontal angles, and a bit greater in vertical angle

measurements. Mean values of these errors are

smaller than 1º. Thus, the calibrated eye tracker

fulfils the accuracy specified by the manufacturer.

The eye angular deviation when executing the

tracking task was obtained in a similar way. At each

time, the theoretical eye line of gaze corresponding

to the moving target was calculated and it was

compared with actual gaze line measured by the eye-

tracker. Vertical and horizontal angle deviations

were analyzed.

Table 1: Errors in the static task. These errors quantify the

accuracy of the reference conventional eye-tracker.

System Error (standard deviation)

Subject Horizontal (º) Vertical (º)

s1 0.42 0.58

s2 0.51 0.53

s3 0.95 1.52

s4 0.67 0.47

s5 0.57 0.84

Mean 0.65 0.88

Table 2: Errors of the horizontal and vertical angles for the

dynamic tracking task.

Tracking error (standard deviation)

Subject Horizontal (º) Vertical (º)

s1 0.53 0.48

s2 0.49 0.61

s3 0.49 0.59

s4 0.56 0.77

s5 0.61 0.70

Mean 0.54 0.64

0 50 100 150 200 250

100

120

140

160

180

200

220

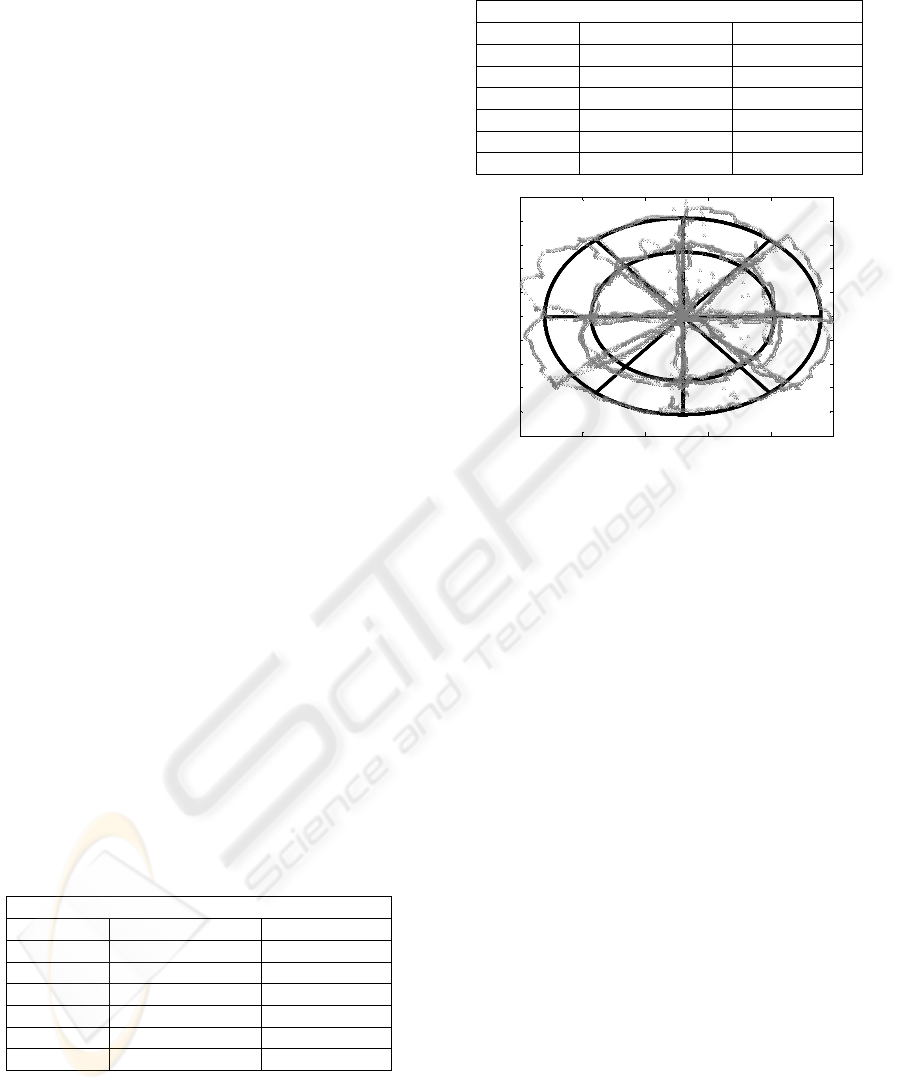
Figure 3: Deviations in tracking task. Black solid line is

the trajectory of the target on the screen. Grey markers

represent the actual gaze direction.

Figure 3 shows an example of the results in an

individual dynamic task. The black solid line

represents the actual trajectory of the moving target

on the screen. The grey markers represent the

intersection of measured gaze line with the screen.

This way, the distances between the actual target

location and the one obtained from the measured

gaze line quantifies the gaze error when executing

the task. These distances were normalized as angles

(by means of the distance to the screen). The

“accuracy” of the tracking task was quantified by the

standard deviation of the measured angular

deviations for both vertical and horizontal angles.

Table 2 shows the errors for each user as well as

the mean of the sample. The errors are smaller than

1º in all cases, both for vertical and horizontal

angles. In fact the order of magnitude is the same as

the accuracy of the conventional eye-tracker in static

calibrated tasks.

Note that the errors measured in the dynamic

task have two sources of variance. First, we can

expect some instrumental error associated to the

accuracy of the eye-tracker device. This error can be

estimated by the results obtained in the static task

and is quantified in Table 1. Second, the dynamic

errors depend on the subjects’ ability to effectively

follow the moving target. The errors described in

table 2 are the associated to both sources.

A SIMPLE DEVICE TO MEASURE GAZE ANGLES IN VISUAL TASK ANALYSES

123

By comparing the magnitude of static errors (Table

1) and total errors (Table 2), we can see that these

errors are similar. Thus, the mean errors in the static

tasks are around 0.65º for horizontal angles and

around 0.88º for the vertical ones. The errors

estimated in the tracking tasks were similar (0.54º

and 0.64º, respectively). We can conclude that the

subjects effectively follow the moving target during

the experiments, in any case within the margin of

accuracy of a conventional eye-tracker.

Therefore, the main hypothesis of operation of

the proposed system is confirmed: it is possible to

measure the relative gaze angles from the

movements of the head if the location and motion of

the target is known.

5 CONCLUSIONS

AND DISCUSSION

Despite the extensive development of the eye

tracking techniques, the available commercial

devices present some problems, mainly related with

a robust recognition of eye characteristics, their

sensitivity to head movements and the necessity of

previous calibrations. All these factors have

influence on the devices’ accuracy as well as on the

reliability and feasibility of their use in poorly

controlled environments.

However, some specific applications in the filed

of optometry use only specific information about

gaze lines that do not need complex equipment. This

is the case of the visual maps measurement, an

application of eye-tracking techniques to analyze the

user response to progressive addition lenses. In these

applications, the use of specifics technologies could

avoid the drawbacks of conventional equipments.

In this paper we propose an effective and simple

technique for the accurate measurement of the

relative gaze angles while executing visual tasks.

The system operates on a simple principle: the use of

a visual target with controlled location and the

measurement of head movements. Determining once

the location of the subject’s eyes in a reference

posture, the estimation of gaze direction is feasible

just with head movement measurement.

The use photogrammetric techniques allows a

very accurate measurement of these movements,

with an instrumental error lower than 0.5º. However,

the system reliability depends on the subjects’

effectiveness on tracking the target.

The experimental validation with subjects

demonstrated accurate target tracking, with an error

below the accuracy of the conventional eye-tracker

used in the experimentation.

Therefore, the proposed technique permits a

simple and robust measurement of the visual maps,

with the same accuracy as the measure performed

with a complex and expensive equipment.

ACKNOWLEDGEMENTS

This research has been partially supported by the

Spanish Ministry of Science and Education Grant

DPI2006-14722-C02-01 (A. Page).

REFERENCES

Abadi, R.V. 2006. Vision and eye movements. Clinical

and Experimental-Optometry, 89, 2, pp 55-56

Abdel-Aziz, Y. I. and Karara, H. M., 1971. Direct linear

transformation from comparator coordinates into

object-space coordinates, in Proceedings ASP/UI

Symposium on Close-Range Photogrammetry

(American Society of Photogrammetry, Falls Church,

VA) pp 1-18

Ahmed, M. and Farag, A., 2005. Nonmetric Calibration of

Camera Lens Distortion: Differential Method and

Robust Estimation. IEEE Transactions on Image

Processing, 14, 8, pp 1215-1230

Beymer, D. and Flickner, M., 2003. Eye gaze tracking

using an active stereo head, in: Proc. of the IEEE

Conference on Computer Vision and Pattern

Recognition, II, Madison, WI, pp. 451–458

Engström, J., Johansson, E. and Östlund, J., 2005. Effects

of visual and cognitive load in real and simulated

motorway driving. Transportation Research: Part F, 8,

pp 97-12

Han, Y., Ciuffreda, K. J., Selenow, A. and Ali, S. R.,

2003. Dynamic interactions of eye and head

movements when reading with single-vision and

progressive lenses in a simulated computer-based

environment. Invest. Ophthalmol. Vis. Sci. 44, pp 1534–

1545

Hartley, R. and Zisserman, A., 2004. “Multiple View

Geometry in Computer Vision”. Cambridge

University Press.

Hutchings, N., Irving, E., Jung, N., Dowling, L. and

Wells, K., 2007. Eye and head movement alterations

in naïve progressive addition lens wearers. Ophthal.

Physiol. Opt., 27, pp 142–153

Land, M.F. and McLeod,,P., 2000. From the eye to

actions: how batsmen hit the ball. Nature

Neuroscience, 3, pp 1340-1345

Lohse, G.L., 1997. Consumer eye movement patterns on

Yellow Pages advertising, Journal of Advertising. 26,

1, pp 61-73

BIODEVICES 2008 - International Conference on Biomedical Electronics and Devices

124

Morimoto, C.H. and Mimica, M.R.M., 2005. Eye gaze

tracking techniques for interactive applications.

Computer Vision and Image Understanding 98, pp 4–24

Page, A., De Rosario, H., Mata, V., Hoyos, J. and Porcar,

R., 2006. Effect of marker cluster design on the

accuracy of human movement analysis using

stereophotogrammetry. Med Biol Eng Comput. 44, pp

1113-1120

Richardson, D.C. and Spivey, M., 2004a. Eye tracking:

Characteristics and methods. In G. Wnek & G. Bowlin

(Eds.) Encyclopedia of Biomaterials and Biomedical

Engineering, pp.568-572. New York: Marcel Dekker, Inc.

Richardson, D.C. and Spivey, M., 2004b. Eye tracking:

Research areas and applications. In G. Wnek & G.

Bowlin (Eds.) Encyclopedia of Biomaterials and

Biomedical Engineering, pp. 573-582. New York:

Marcel Dekker, Inc.

Ripoll, H., Kerlirzin, Y., Stein, J. and Reine, B., 1995.

Analysis of information processing, decision making,

and visual strategies in complex problem solving sport

situations. Human Movement Science, 14, pp 325-349

Selenow, A., Bauer, E. A., Ali, S. R., Spencer, L. W. and

Ciuffreda, K. J., 2002. Assessing visual performance

with progressive addition lenses. Optom. Vis. Sci. 79,

pp 502–505

Sesin, A., Adjouadi, M. and Ayala, M., 2003. A

calibrated, real-time eye gaze tracking system as an

assistive system for persons with motor disability. 7th

world multiconference on systemics, cybernetics and

informatics, VI, proceedings, pp 399-404

Schnipke, S.K. and Todd, M.W., 2000. Trials and

tribulations of using an eye-tracking system, in: Proc.

ACM SIGCHI—Human Factors in Computing

Systems Conference, pp. 273–274

Treistman, J. and Gregg, J. P., 1979. Visual, verbal, and

sales responses to print ads. Journal of Advertising

Research, 19, 4, pp 41-44

Woltring, H.J., Long, K., Osterbauer, P.J. and Fuhr, A.W.,

1994. Instantaneous helical axis estimation from 3-D

video data in neck kinematics for whiplash

diagnostics. Journal of Biomechanics, 27, 12, pp 1415-

1432

A SIMPLE DEVICE TO MEASURE GAZE ANGLES IN VISUAL TASK ANALYSES

125