ON EXTRACTION OF NUTRITIONAL PATTERNS (NPS) USING
FUZZY ASSOCIATION RULE MINING
M. Sulaiman Khan
1, 2
, Maybin Muyeba
1
1
School of Computing, Liverpool Hope University, Liverpool, UK
Frans Coenen
2
2
Department of Computer Science, University of Liverpool, UK
Keywords: Association rules, nutritional patterns, fuzzy association rules, nutrients.
Abstract: This paper proposes a framework for mining market basket data to generate Nutritional Patterns (NPs) and a
method for analysing generated nutritional patterns using Fuzzy Association Rule Mining. Edible attributes
are filtered from transactional input data by projections and are then converted to Recommended Dietary
Allowance (RDA) numeric values. The RDA database is then converted to a fuzzy database that contains
expended normalized fuzzy attributes comprising of different fuzzy sets. Analysis of nutritional information
is performed either from normal generated association rules or from a converted fuzzy transactional
database. Our approach uses prototype support tool that extract Nutritional Patterns (NPs) and signifies the
level of nutritional content in an association rule per item. The paper presents various performance tests and
interestingness measures to demonstrate the effectiveness of the approach and concludes with experimental
results and discussion on evaluating the proposed framework.
1 INTRODUCTION
Association Rule Mining (ARM) (Agarwal, 1993) is
a popular data mining technique that has been used
to determine customer buying patterns from market
basket data. General association rules are of the form
XÆY, which means customers who buy X also buy
Y, with given support and confidence measures. A
support measure is used to determine the number of
transactions that include all items in the antecedent
(X value) and the consequent (Y value) parts of the
rule, while a confidence measure is the ratio of
support to the number of transactions that include all
items in the antecedent.
The discovered rules indicate
patterns of associating items. Such rules can be helpful
in shelf arrangements, advertisement, sales promotion
etc. However, nowadays health concerns are becoming
increasingly important to a large community of people
including health practitioners, sporting organizations,
governments and recently supermarkets. In data
mining, association rules have been used to determine
buying patterns (to the shop owner’s benefit) but not
nutritional pattern in general (to the customers health
benefit).
People have recently become “healthy eating”
conscious, but largely they are unaware of qualities,
limitations and above all, constituents of food. For
example, how often do people who buy baked beans
bother with nutritional information other than
looking at expiry dates, price and brand name?
Unless the customer is diet conscious, there is no
explicit way to determine nutritional requirements
and consumption patterns. There are many dietary
schemes and programmes that individuals follow
that helps them determine how healthy they are but
do not critically analyse nutritional elements that
may affect their health. It is known that certain
nutritional chemical elements when taken in large
quantities do alter genetic material of a person, but
also other elements are known to be more important
for health than others.
Nowadays, nutritional information is usually
labeled on supermarket products but is not used to
determine actual nutritional patterns of every given
customer transaction. This information would be
useful for individual customers own health
evaluation, supermarkets own reports on likely
healthy buying patterns and many health related
34
Sulaiman Khan M. and Muyeba M. (2008).
ON EXTRACTION OF NUTRITIONAL PATTERNS (NPS) USING FUZZY ASSOCIATION RULE MINING.
In Proceedings of the First International Conference on Health Informatics, pages 34-42
Copyright
c
 SciTePress

organizations including government health
ministries. As modern society is concerned with
health issues, association rules can be used to
determine nutritional patterns by analysing product
nutritional information, using market basket data.
The approach signifies the level of nutritional
content in an association rule per item.
Most algorithms in the literature have concentrated
on improving performance through efficient
implementations of the modified Apriori algorithm
(Bodon, 2003), (Lee, 2003), (Coenen, 2004), (Wang,
2004). Although improving performance and
efficiency of various ARM algorithms is important,
determining Nutritional Patterns (NPs) from
customer transactions and association rules is also
important. Extracting health related information
using association rules from market basket data has
mostly been overlooked.
In this paper we propose a fuzzy based approach
for extracting nutritional patterns using fuzzy
association rule mining, where a transactional
database is converted into a database that contains
the average RDA of nutrient values per item. This
database is then converted into a fuzzy database with
fuzzy attributes, according to the nutrients intake.
The fuzzy database contains the actual contribution
of nutrients per transaction or fuzzy membership
degrees in fuzzy sets for each particular item (e.g.
values 0.0, 0.3, 0.5, 0.2, 0.0 for fuzzy attributes very
low, low, ideal, high and very high respectively) as
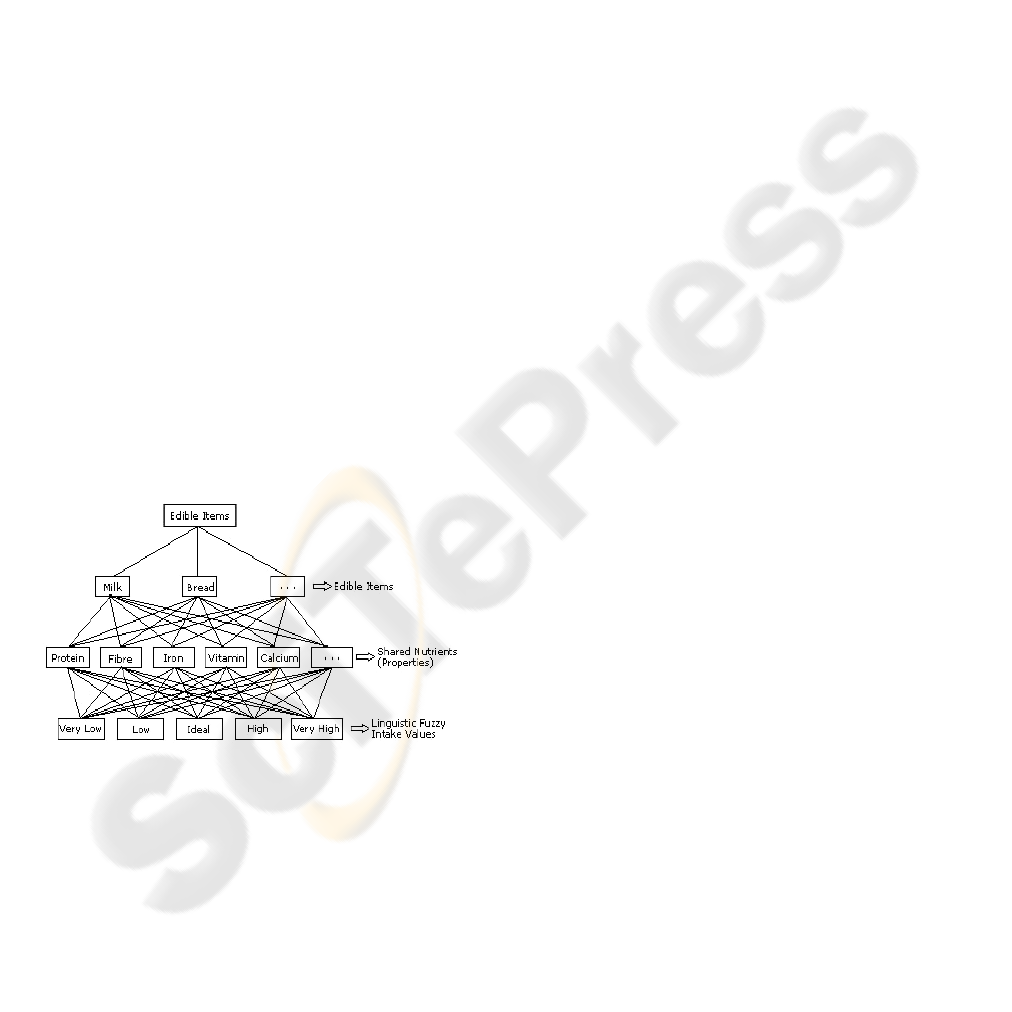
shown in the figure 1.
Figure 1: Edible items, Nutrients & Fuzzy Intervals.
We show the effectiveness of this new method by
applying it on different datasets. Our contributions
are that edible attributes in market basket data are
used with an RDA table, a fuzzy normalization
process and correlation analysis produce effective
rules and records good performance.
The paper is organised as follows: section 2
presents background and related work; section 3
gives a problem definition; section 4 discusses the
proposed methodology; section 5 reviews
experimental results, and section 6 concludes the
paper with directions for future work.
2 BACKGROUND AND
RELATED WORK
Many applications of association rule mining have
been proposed in medical domain (Xie, 2005),
(Yuanchen, 2006), (Lavrac, 1996), (Delgado, 2000)
but most of the researches in the literature have
concentrated on improving performance through
efficient implementation than producing effective
rules (Bodon, 2003), (Lee, 2003), (Coenen, 2004),
(Wang, 2004). Again, in almost all ARM algorithms,
thresholds (both confidence and support) are crisp
values. This support specification may not suffice
for queries and rule representations that require
generating rules that have linguistic terms such as
“low/Ideal/High for protein intake” etc. Fuzzy
approaches (Chen, 2002), (Wai, 1999), (Xie, 2005),
(Guenesei, 2001) deal with quantitative attributes
(Srikant, 1996) by mapping numeric values to
Boolean values. Detailed overviews for fuzzy
association rules are given in (Chen, 2002), (Wai,
1999), (Dubois, 2006).
Effective and efficient fuzzy algorithms
supporting the mining process, i.e. the extraction of
interesting associations from a database, have
received less attention in the fuzzy community. This
might be explained to some extent by the fact that,
for fuzzy extensions of association analysis, standard
algorithms can often be used or at least adapted in a
relatively straightforward way. Still, some
contributions have been made in this field. For
instance, (Muyeba, 2006) describe the process of
fuzzy association rules to obtain healthy buying
patterns using binary Apriori algorithm.
Mining nutrient associations among itemsets is a
new type of ARM technique which attempts to
investigate Nutritional Patterns (NPs) by analysing
nutrition consumption patterns. In (Xie, 2005), fuzzy
associations are presented, where a reduced table is
used to effectively minimise the complexity of
mining such rules. The authors also present mining
for nutrients in the antecedent part of the rule, but it
is not clear how the fuzzy nutrient values are
aggregated and largely, how membership functions
are used. Our algorithm’s ultimate goal is to
determine customers’ buying patterns for healthy
foods, which can easily be evaluated using RDA
standard tables. Other related work deals with
ON EXTRACTION OF NUTRITIONAL PATTERNS (NPS) USING FUZZY ASSOCIATION RULE MINING
35

building a classifier using fuzzy ARs in biomedical
applications (Yuanchen, 2006).
Fuzzy association rules have been used for
medical data mining (Xie, 2005), (Lavrac, 1996),
(Delgado, 2000), but we propose a novel approach
to determine whether customers are buying healthy
food, which can easily be evaluated using required
daily allowance (RDA) standard tables.
3 PROBLEM DEFINITION
In this section a sequence of formal definitions is
presented to: (i) describe the concept of fuzzy
association rule mining and (ii) the fuzzy approach
adopted by the authors. The normalization process
for Fuzzy Transactions
)(T
′
and rules interestingness
measures will also be discussed later in this section.
3.1 Fuzzy Association Rules
Mining fuzzy association rules is the discovery of
association rules using fuzzy sets such that
quantitative attributes can be handled (Dubois,
2006). A fuzzy quantitative rule represents each item
as (item, value) pair. Fuzzy association rules are thus
expressed in the following form:
If X is A satisfies Y is B
For example if (age is young) Î (salary is low)
where age and salary represents X and Y, and young
and low are the discretised/linguistic values for
attributes age and salary respectively representing A
and B.
In the above rule,
},...,,{
21 n
xxxX = and
},...,,{
21 n
yyyY =
are itemsets, where
IYIX ⊂⊂ , , and ∅=∩YX . Sets
},...,,{ 21 xnxx fffA =
and
},...,,{ 21 ynyy fffB =
contain the fuzzy sets associated with the
corresponding attributes in X and Y, for example
(protein, low), (protein, ideal), (protein, high). The
semantics of the rule is that when 'X is A' is
satisfied, we can imply that 'Y is B' is also satisfied,
which means there are sufficient records that
contribute their votes to the attribute fuzzy set pairs
and the sum of these votes is greater than the user
specified threshold which could be crisp or fuzzy.
For a given database
D with transactions
},...,,,{ 321
n
ttttT =
with items
},...,,,{
||321 I
iiiiI =
and converted fuzzy transactions
},...,,,{ 321
n
ttttT
′
′
′
′
=
′
with attributes
},...,,,{
||321 P
ppppP
=
and the fuzzy sets
},...,,{
21 m
fpfpfpF
=
associated with each
attribute in P.
Table 1: Set of ordinary transactions.
D
i
1
i
2
i
3
t
1
1 0 1
t
2
0 1 0
t
3
1 1 1
… … … …
A fuzzy transaction is a special case of transformed
ordinary transaction (table 1) and nonempty fuzzy
subset of P where
PT ⊆
′
. In table 2 an
item
j
p
and transaction
k
t
′
contains a value v
(membership degree) in [0, 1]. The membership
degree of
j
p in
k
t is ))((
ljk
vpt . Without loss of
generality, we also define edible set of items
IE ⊆
where any
Ei
j
∈
consists of quantitative
nutritional information
∪
||
1
P
p
P
j
i
=
, where each
p
j
i is
given as standard RDA numerical ranges and
consists of |P| nutrients.
Table 2: Set of edible fuzzy transactions.
E fp
1
(v
1
)
fp
1
(v
2
)
fp
1
(v
3
)
F
p
1
(v
4
)
F
p
1
(v
5
)
fp
2
(v
1
)
fp
2
(v
2
)
fp
2
(v
3
)
fp
2
(v
4
)
fp
2
(v
5
)
t
/
1
0.
0
0.
7
0.
3
0.
0
0.
0
0.
0
0.
0
0.
8
0.
2
0.
0
t
/
2
1.
0
0.
0
0.
0
0.
0
0.
0
1.
0
0.
0
0.
0
0.
0
0.
0
t
/
3
0.
0
0.
0
0.
9
0.
1
0.
0
0.
0
0.
0
0.
8
0.
2
0.
0
… … … … … … … … … … …
Each quantitative item
j
p
is divided into various
fuzzy sets
)(
j
pf
and
),( vlm
denotes the
membership degree of
v in the fuzzy set l ,
1),(0
≤
≤
vlm
as shown in table 2.
HEALTHINF 2008 - International Conference on Health Informatics
36

3.1.1 Fuzzy Transactions Normalization
Process
As mentioned above each quantitative item
j
p
in
k
t
′
is divided into various fuzzy sets )(
j
pf and
),( vlm denotes the membership degree of v in the
fuzzy set
l ,
1),(0 ≤≤ vlm
. For each fuzzy
transaction
Et ∈
′
(edible items), a normalization
process to find significance of an items contribution
to the degree of support of a transaction in order to
guarantee a partition of unity is given by the
equation (1):
∑
=
′
′
=
)(
1
))(,(
)(,(
'
j
pf
l
jk
jk
ptlm
ptlm
m
(1)
Without normalisation, support of an individual
fuzzy item could increase in a transaction. The
normalisation process ensures fuzzy membership
values for each nutrient are consistent and are not
affected by boundary values.
3.1.2 Fuzzy Support and Confidence
The problem of mining fuzzy association rules is
given following a similar formulation in (Kuok,
1998). To generate Fuzzy Support (FS) value of an
item set X with fuzzy set A, we use the equation (2):
||
])[(
),(
E
xtm
AXFS
ji
Tt
Xx
i
j
′
∏
=
∑
∈
∈
(2)
A quantitative rule represents each item as <item,
value> pair. In the above equation we have used
arithmetic mean averaging operator for fuzzy
nutrients aggregation of candidate itemsets in a
transactional database and used multiplication
“
mul ” operator for fuzzy union of candidate items
in a transaction.
min or max operators can also be
used but
mul provides us the simplest and
reasonable results as shown in table 3. In case when
the fuzzy transactions are not normalized
mul
is
more suitable because it takes the degrees of all
items in a transaction into account.
Table 3: Effect of fuzzy mul operator.
i
1
i
2
i
3
i
4
Max Min Mul
0.2 0.6 0.7 0.9
Æ
0.9 0.2 0.075
0.9 0.8 0.5 0.6
Æ
0.9 0.5 0.216
0.7 0.0 0.75 0.8
Æ
0.8 0.0 0.0
0.3 0.9 0.7 0.2
Æ
0.9 0.2 0.037
For a rule
>>→<
<
BYAX ,, , the fuzzy
confidence value (FC) where
CBAZYX
=
∪
=
∪ , is given by equation (3):
])[(
])[(
),,(
ji
Tt
Xx
ji
Tt
Xz
xtm
ztm
BYAXFC
i
j
i
j
′
∏
′
∏
=>>→<<
∑
∑
′
∈
′
∈
′
∈
′
∈
(3)
where each
}{ YXz ∪
∈
. For our
approach,
EYX ⊂,
, where E is a projection of
edible items from
D . Depending on the query,
each item
j
i specified in the query and belonging to
a particular transaction, is split or converted into |P|
nutrient parts
∪
||
1
||1,
P
p
p
j
Iji
=
≤≤
. For each
transaction t, the bought items contribute to an
overall nutrient p by averaging the total values of
contributing items i.e. if items
43
,ii and
7
i are in a
transaction
1
t and all contain nutrient p=5 in any
proportions, their contribution to nutrient 5 is
∑
3
||
5
j
i
, j
∈
{3,4,7}. These values are then
aggregated into an RDA table with a schema of
nutrients (see table 5, section 4) and corresponding
transactions. We use the same notation for an item
j
i with nutrient p,
p
j
i as item or nutrient
j
p in the
RDA table. Given that items
j
p
are quantitative
(fuzzy) and we need to find fuzzy support and fuzzy
confidence as defined, we introduce membership
functions for each nutrient or item since for a normal
diet intake, ideal intakes for each nutrient vary.
However, five (5) fuzzy sets for each item are
defined as {very low, low, ideal, high, very high}
based on expert analysis on nutrition.
Based on this analysis, examples of fuzzy
membership functions for nutrient Protein is shown
in figure 1. There are many different types of
membership function and the type of representation
ON EXTRACTION OF NUTRITIONAL PATTERNS (NPS) USING FUZZY ASSOCIATION RULE MINING
37

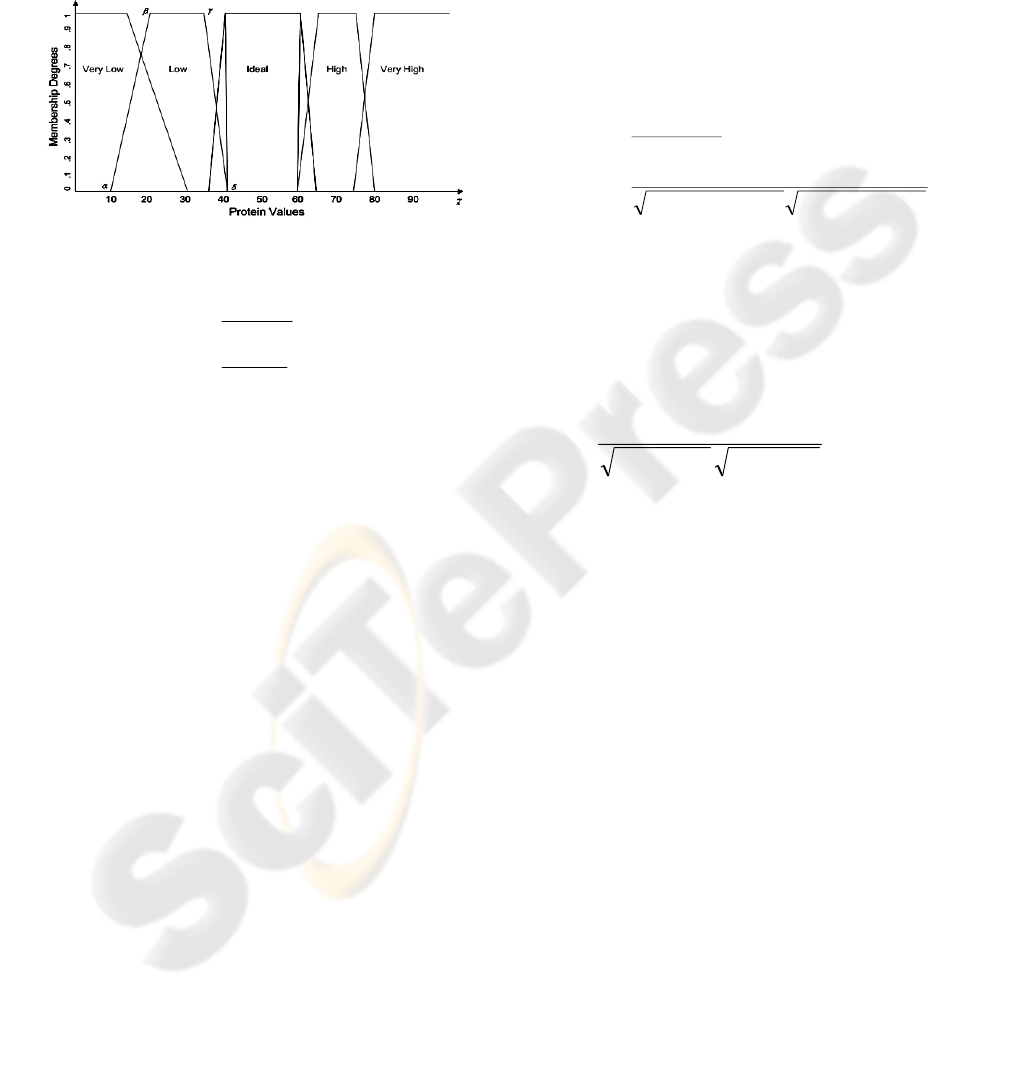
of the membership function depends on the nature of
the fuzzy set. In figure 2 the functions assume a
trapezoidal shape since nutrient values in excess or
in deficiency mean less than ideal intake according
to expert knowledge. Ideal nutrients can assume
value 1 naturally, but this value could be evaluated
computationally to 0.8, 0.9 in practical terms.
Figure 2: Fuzzy membership functions.
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
∈
−
−
∈
−
−
∈
=
otherwise
x
x
x
x
x
x
,0
],[,
)(
)(
],[,
)(
)(
],[,1
),,,,(
δγ
γδ
δ
βα
αβ
α
γβ
δγβαμ
(4)
Equation 4 (Paetz, 2002) represents all nutrient
membership degrees of a nutrient value “x”. The
input database value x has “ideal” values of a
nutrient between
β
and
γ
, with lowest value
α
and
highest value
δ
. The task is to determine a
membership value of x in equation 4.
Note that equation 4 gives values equal to
),( vlm
in equations 1, 2 and 3. We can then handle any
query after a series of data transformations and
fuzzy function evaluations of associations between
nutritional values. For missing nutrient values or so
called “trace” elements, the fuzzy function evaluated
zero degree membership.
3.2 Interestingness Measures
Measures of interestingness other than standard
support and confidence are required in order to
evaluate the quality of fuzzy association rules. The
quality measure for a rule to be interesting is called
certainty factor (). A rule can be considered
interesting if the fuzzy set union of antecedent and
the consequent has enough significance and the rule
has adequate certainty. A measure of significance
for a rule is similar to equation (3) and we have
adopted it as the confidence of a rule. The certainty
factor is determined by computing the fuzzy
correlation of antecedent and the consequent of the
rule. We have used Pearson’s product-moment
correlation coefficient between attributes which is
different from the general statistical usage of
correlation because in association rule
mining
XYYX ⇒
≠
⇒
.
The correlation
),( YXCorr between two
variables X and Y with expected values E(X) and
E(Y) and standard deviations
x
σ
and y
σ
is
defined as:
2222
)()()()(
)().().(
),(
),(
),(
YEYEXEXE
YEXEYXE
YXCorr
yx
YXCov
YXCorr
−−
−
=
=
σσ
where E is the expected value of the variables and
cov is covariance. We can transform the above
correlation equation to find the certainty factor
between two or more fuzzy attributes and can
calculate fuzzy correlation as:
),(),(
),,,(
),,,(
BYVarAXVar
BYAXCov
BYAXCorr
Fuzzy
><><
=
><>
<
(5)
The value of correlation ranges from -1 to +1. Value
-1 means no correlation and +1 means maximum
correlation. In our problem, only positive values can
be considered as the degree of relation. As the
certainty value increases from 0 to 1, the more
related the attributes are and consequently the more
interesting they are. Therefore if the rule “IF Protein
is low THEN Vitamin A is high” holds, then the
certainty value should be at least greater than zero.
This could mean customers prefer to buy more
vitamin related items to protein ones and the HBP
value is simply the certainty value obtained (see
section 6.1
4 PROPOSED METHODOLOGY
The proposed methodology consists of various
phases, each of which is evaluated using fuzzy sets
for quantitative attributes (Nutrients) as mentioned
earlier. We have developed an algorithm called
Fuzzy Healthy Association Rule Mining algorithm
(FHARM). FHARM can deal with other kinds of
transactional and relational databases to generate
HEALTHINF 2008 - International Conference on Health Informatics
38

fuzzy association rules using quantitative attributes.
We have discovered two techniques to obtain
Nutritional Patterns as described in the next sections.
4.1 Nutritional Fuzzy ARM Mining
To mine from the transactional file (table 4), input
data is projected into edible database on-the-fly
thereby reducing the number of items in the
transactions and possibly transactions too. The latter
occurs because some transactions may contain non-
edible items which are not needed for nutrition
evaluation. This new input data is converted into an
RDA transaction file (table 5) using RDA table
(definition 6) with each edible item expressed as a
quantitative attribute and then aggregating all such
items per transaction (see definition 2, equation 1).
Table 4: Market Basket
Data.
TID Items
1 X, Z
2 Y
3 X,Y, Z
4 ..
Table 5: Converted RDA
transactions.
TID Pr Fe Ca Cu
1 45 150 86 28
2 9 0 47 1.5
3 54 150 133 29.5
4 .. .. .. ..
At this point, two solutions may exist for the next
mining step. One is to discretised nutrients into
intervals and converts RDA Transactions into
discretised transactions with boolean values (Table
6) for each nutrient and corresponding value for
each interval per nutrient. Each transaction then
(table 6), will have repeated fuzzy values {very low,
low, ideal, high, very high} for each nutrient present
in every item of that transaction. Table 6 actually
shows only two nutrients.
Table 6: Discretised (Boolean) transaction file.
Protein (Pr) Iron (Fe)
TID
VL L Ideal H VH VL L Ideal H VH
…
1 0 1 0 0 0 0 0 1 0 0 …
2 1 0 0 0 0 1 0 0 0 0 …
3 0 0 1 0 0 0 0 1 0 0 …
4 … … … … … … … … … … …
Thus nutrients can have only values [0, 1] and only 1
intake value out of five in table 6, which represents
its complete membership in that interval. The
discretised boolean data can be mined by any binary
type association rule algorithm to find frequent item
sets and hence association rules. This approach only
gives us, for instance, the total support of various
fuzzy sets per nutrient and not the degree of support
as expressed in equations 2 and 4.
The other approach (which we have adopted) is to
convert RDA transactions (table 5) to linguistic
values for each nutrient and corresponding degrees
of membership for the fuzzy sets they represent
above or equal to a fuzzy support threshold. Each
transaction then (table 7), will have repeated fuzzy
values {very low, low, ideal, high, very high} for
each nutrient present in every item of that
transaction.
Table 7: Linguistic (Fuzzy) transaction file.
Protein (Pr) Iron (Fe)
TID
VL L Ideal H VH VL L Ideal H VH
…
1
0.0 0.7 0.3 0.0 0.0 0.0 0.0 0.8 0.2 0.0
…
2
1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0
…
3
0.0 0.0 0.9 0.1 0.0 0.0 0.0 0.8 0.2 0.0
…
4 … … … … … … … … … … …
Table 7 actually shows only two nutrients. A data
structure is then used to store these values (linguistic
value and degree of membership) and large itemsets
are found based on the fuzzy support threshold.
To obtain the degree of fuzzy support, we use
equations 2 and 4 on each fuzzy set for each nutrient
and then obtain ARs (Nutritional Patterns) in the
normal way e.g.
IF Protein intake is High AND Vitamin A intake is Low
THEN Fat intake is High.
4.2 Rule Query on Nutrient
Associations
To mine a specific rule, XÆY, for nutritional
content, the rule base (table 8) is scanned first for
this rule and if found, converted into an RDA table
(table 9) otherwise, the transactional database is
mined for this specific rule. The latter involves
projecting the database with attributes in the query,
thus reducing the number of attributes in the
transactions, and mining as described in 4.1.
In the former case, NPS are generated and the
rule is stored in the new rule base with appropriate
support, for example [proteins, ideal] Æ
[carbohydrates, low], 35%. A rule of the form “Diet
Coke Æ Horlicks, 24%” could be evaluated to many
rules including for example, [Proteins, ideal] Æ
[Carbohydrates, low], 45%; where, according to rule
representations shown in section 3, X is “Proteins”,
A is “ideal” and Y is “Carbohydrates”, B is “low”
etc. The same transformation to an RDA table
occurs and the average value per nutrient is
calculated before conversion to membership degrees
or linguistic values. Using equations 2, 3, 4 and 5,
we evaluate final rules \expressed as linguistic
ON EXTRACTION OF NUTRITIONAL PATTERNS (NPS) USING FUZZY ASSOCIATION RULE MINING
39

values. The following example shows a typical
query as described in 4.1 where TID is transaction
ID, X,Y, Z are items and P (protein), Fe (Iron), Ca
(calcium), Cu (Copper) are nutritional elements and
support (Supp) and confidence (Conf) is given:
Table 8: Rule base.
Table 9: RDA table and HBP
rule.
P
r
Fe Ca Cu ..
X
ÆY 20 10 30 60 ..
.. .. .. .. .. ..
Rules Support
XÆY 24%
YÆZ 47%
X,YÆZ 33%
.. ..
Î
Nutritional Pattern
XÆY [Proteins, Very Low] Æ [Carbohydrates, Low],
Supp=45%, Conf=20%;
5 EXPERIMENTAL RESULTS
In order to show the defined frameworks
effectiveness, we performed experiments using the
prototype tool (figure 3) using T10I4D100K dataset
containing simulated market basket data [generated
by the IBM Almaden Quest research group]
(Agrawal, IBM). The data contains 100K
transactions and 1000 items. We considered 600
edible items out of the 1000 and used a real
nutritional standard RDA table to derive fuzzy sets.
Nutritional Patterns are then generated from
T10I4D100K dataset using methodology as
described in section 4.
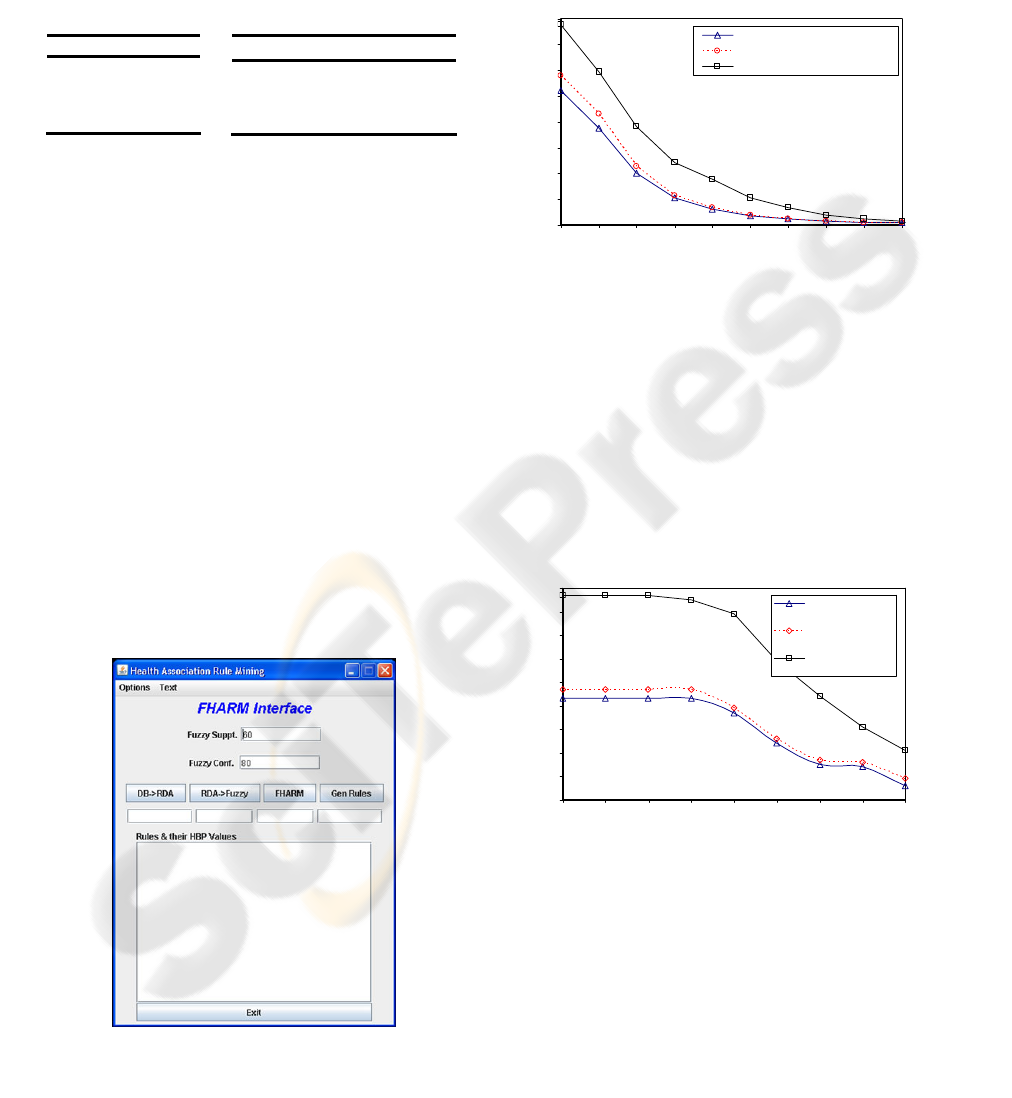
Figure 3: Prototype Tool.
5.1 Experiment One
Experiment for method mentioned in 4.1 shows how
our approach produces NPs in terms of interesting
rules. We use all the 27 nutrients with T10I4D100K
dataset.
0
50
100
150
200
250
300
350
400
0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 0.55 0.6
Fuzzy Support
Frequent Itemsets
Fuzzy ARM with normalisation
Fuzzy ARM without Normalisation
Quantitative ARM (Discrete Method)
Figure 4: Number of Interesting Rules using fuzzy
correlation.
Figure 4 shows difference between number of
frequent items produced by fuzzy method (with and
without normalisation) and discrete method
(discretised boolean data). From the results, it is
clear that the approach with boolean data produces
more and irrelevant rules than the fuzzy approach.
This is because using discrete method we cannot get
the actual membership degree of nutrients intake for
different intervals in each transaction thus
considering full membership in any of the interval.
10
20
30
40
50
60
70
80
90
100
0.10.20.30.40.50.60.70.80.9
Fuzzy Confidence
Interesting Rules
Fuzzy ARM (with
normalisation)
Fuzzy ARM (without
normalisation)
Quantitative ARM
(Discrete Method)
Figure 5: Number of Interesting Rules using fuzzy
confidence.
Figure 5 and Figure 6 shows the number of
interesting rules using user specified fuzzy
confidence and fuzzy correlation values
respectively. Correlation has not been applied to
quantitative ARM algorithm due to the boolean data
and so only Fuzzy approaches (with and without
normalisation) have been shown in figure 6.
HEALTHINF 2008 - International Conference on Health Informatics
40

Overall, the approach presented here is effective,
efficient and could be very useful for both the
customer and health organizations.
REFERENCES
Agrawal, R., Srikant, R., IBM. Quest Synthetic Data
Generator. IBM Almaden Research Center,
http://www.almaden.ibm.com/cs/projects/iis/hdb/Proje
cts/data_mining/datasets/data/assoc.gen.tar.Z
Agrawal, R., Imielinski, T., Swami, A. N., 1993 Mining
Association Rules Between Sets of Items in Large
Databases. In Proceedings of the 1993 ACM SIGMOD
Conference on Management of Data, (1993), 207-216.
Bodon, F., 2003. A Fast Apriori Implementation. IEEE
ICDM Workshop on Frequent Itemset Mining
Implementations (FIMI'03), Melbourne, Florida, USA,
Vol. 90.
Lee, C.-H., Chen, M.-S., Lin, C.-R., 2003. Progressive
Partition Miner: An Efficient Algorithm for Mining
General Temporal Association Rules. IEEE
Transactions on Knowledge and Data Engineering,
Vol. 15, No. 4, 1004 - 1017.
Chen, G., Wei, Q., 2002. Fuzzy Association Rules and the
Extended Mining Algorithms. Information Sciences-
Informatics and Computer Science: An International
Journal archive, Vol. 147, No. (1-4), 201 - 228.
Wai, A.-H., Chan, K., 1999. Farm: A Data Mining System
for Discovering Fuzzy Association Rules. In
Proceedings of the 18th IEEE Conference on Fuzzy
Systems, 1217-1222.
Srikant, R., Agrawal, R., 1996. Mining Quantitative
Association Rules in Large Relational Tables. In
Proceedings of ACM SIGMOD Conference on
Management of Data. ACM Press, 1-12.
Dubois, D., Hüllermeier, E., Prade, H., 2006. A
Systematic Approach to the Assessment of Fuzzy
Association Rules. Data Mining and Knowledge
Discovery Journal, Vol. 13, No. 3, 167-192.
Xie, D. -W., 2005. Fuzzy Association Rules discovered on
Effective Reduced Database Algorithm. In
Proceedings of IEEE Conference on Fuzzy Systems.
Yuanchen, H., Tang, Y., Zhang, Y-Q., Synderraman, R.,
2006 Adaptive Fuzzy Association Rule Mining for
Effective Decision Support in Biomedical
Applications. International Journal Data Mining and
Bioinformatics, Vol. 1, No. 1, 3-18.
Gyenesei, A., 2001. A Fuzzy Approach for Mining
Quantitative Association Rules, Acta Cybernetical,
Vol. 15, No. 2, 305-320.
Paetz, J., 2002. A Note on Core Regions of Membership
Functions, Proc. of the 3rd Int. Symp. of Medical Data
Analysis (ISMDA 2002), LNCS Vol. 2526, 42-52.
Coenen, F., Leng, P. , Goulbourne, G., 2004. Tree
Structures for Mining Association Rules. Journal of
Data Mining and Knowledge Discovery, Vol. 15, No.
7, 391-398.
Wang, C., Tjortjis, C., 2004. PRICES: An Efficient
Algorithm for Mining Association Rules. In
Proceedings of the 5
th
Conference on Intelligent Data
Engineering Automated Learning, Lecture Notes in
Computer Science Series, Vol. 3177, Springer-Verlag,
352-358.
Lavrac, N., Keravnou ET, Zupan B., 1996. Intelligent data
analysis in medicine and pharmacology. First
International Workshop on Intelligent Data Analysis
in Medicine and Pharmacology (IDAMAP-96).
Dordrecht: Kluwer Academic Publishers.
Delgado, M., Sánchez, D., Vila, MA., 2000. Acquisition
of fuzzy association rules from medical data. In:
Barro, MarõÂn R, editors. Fuzzy logic in medicine.
Wurzburg (Wien): Physical-Verlag, in press.
Muyeba, M., M. Sulaiman Khan, M. Malik, Z., Tjortjis,
C., 2006. Towards Healthy Association Rule Mining
(HARM), A Fuzzy Quantitative Approach, In Proc. 7
th
Conf. Intelligent Data Engineering Automated
Learning, LNCS Series, Vol. 4224, Springer-Verlag,
1014-1022.
Kuok, C., Fu, A., Wong, H., 1998. Mining Fuzzy
Association Rules in Databases. ACM SIGMOD
Record, 27, 41-46.
HEALTHINF 2008 - International Conference on Health Informatics
42