MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE
IMAGE ALGEBRAS
Cytological Specimen Case
I. Gurevich, V. Yashina
Dorodnicyn Computing Center of the Russian Academy of Sciences, Vavilov str., Moscow, Russian Federation
H. Niemann
University of Erlangen-Nuernberg, Lehrstuhl fuer Informatik, Martensstr., Erlangen, Germany
O. Salvetti
Institute of Information Science and Technologies, CNR, 1, Via G.Moruzzi, Piza, 56124, Italy
Keywords: Image mining, image algebras, medical image analysis, pattern recognition in image understanding,
information technologies, automated diagnosis.
Abstract: The paper is devoted to the development and formal representation of the descriptive model of information
technology for automating morphologic analysis of cytological specimens (lymphatic system tumors). The
main contributions are detailed description of algebraic constructions used for creating of mathematical
model of information technology and its specification in the form of algorithmic scheme based on
Descriptive Image Algebras. It is specified the descriptive model of an image recognition task and the stage
of an image reduction to a recognizable from. The theoretical base of the model is the Descriptive Approach
to Image Analysis and its main mathematical tools. It is demonstrated practical application of algebraic
tools of the Descriptive Approach to Image Analysis and presented an algorithmic scheme of a technology
implementing the apparatus of Descriptive Image Algebras.
1 INTRODUCTION
The paper is devoted to the development and formal
representation of the descriptive model of the
information technology for automating morphologic
analysis of cytological specimens of patients with
lymphatic system tumors. The main contribution are
detailed description of algebraic constructions used
for creating of mathematical model of the
information technology and its specification in the
form of an algorithmic scheme based on Descriptive
Image Algebras (DIA). We specify, in particular, the
descriptive model of an image recognition task and
the stage of an image reduction to a recognizable
form.
The theoretical base of the model is the
Descriptive Approach to Image Analysis (Gurevich,
2005) and its main mathematical tools –DIA,
Descriptive Image Models (DIM) and Generating
Descriptive Trees (GDT).
In a sense the results are continuation,
specification and extension of the previous research.
In (Gurevich, et al. 2007) we presented a brief
introduction into the essential tools of the
Descriptive Approach (DIA, DIM, GDT), the
simplified model of an image recognition task based
on multi-model image representation, a descriptive
model of the information technology, and the
descriptive and the structural schemes of the
information technology. The state of the art and
motivation were presented in our previous
publications (Gurevich, et al. 2003, 2006, 2007).
Section 2 illustrates a simplified descriptive
model of an image recognition task based on multi-
model image representation. In section 3 we
introduce operands and operations (and its
operational (semantic) functions) of DIAs and
66
Gurevich I., Yashina V., Niemann H. and Salvetti O. (2008).
MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE IMAGE ALGEBRAS - Cytological Specimen Case.
In Proceedings of the First International Conference on Health Informatics, pages 66-73
Copyright
c
 SciTePress

Descriptive Image Groups (DIG) necessary for
constructing the algebraic model of the
morphological analysis of lymphatic cell nucleuses.
Section 4 presents a descriptive model of the
information technology for automating morphologic
analysis of cytological specimens of patients with
lymphatic system tumors. The technology has been
tested on the specimens from patients with
aggressive lymphoid tumors and innocent tumor.
The results are discussed in Section 4.
The main components of the technology are
described via DIA tools and presented as an
algorithmic scheme. The latter ensures a standard
representation of technologies for intellectual
decision making.
2 DESCRIPTIVE MODEL OF AN
IMAGE RECOGNITION
PROBLEM
The Descriptive Approach provides the following
model for an image recognition process (Gurevich,
2005):
{}
{
}
rxnig
l
ysj
n
i
IPAMI )}({}{
...1
...1
...1
→→→
(1)
{
}
1...
i
n
I
- a set of initial images.
{}
1...
1
r
ig
n
IK⊂∪
,
1...
{}
g
r
K
- a set of classes determined by an image
recognition task,
1...
{}
js
M - a multimodel
representation of each initial image
{
}
1...
i
n
I
. An
algorithm combination
{
}
1...
y
l
A
solves an image
recognition problem, if it puts a set of predicates
{()}
g
irxn
PI
into correspondence to the set of initial
images, where predicate P
g
(I
i
)=a
ig
has the values:
a
ig
=1, if an image I
i
belongs to a class K
g
; a
ig
=0, if
an image I
i
does not belong to a class K
g
; a
ig
=∆, if
an algorithm combination does not establish
membership of an image I
i
to a class K
g
.
Multi-model representation is generated by the
set of GDT. Different ways for constructing multi-
aspect image representations may use different types
of GDT. An image representation becomes a multi-
model one, if it is generated by different types of
GDT.
This model including a training stage is as
follows:
p
0
{
} {}
l
ys
j
a
n
i
pAMI
...1
2
...1
1
)(1
]
2
...[1
)(}{
1
⎯→⎯⎯⎯→⎯
{
}
{}
rxnig
l
ys
j
b
n
n
i
IPpAMI )}({)(}{
...1
0
3
...1
2
)(1
...1]
2
[
2
→⎯→⎯⎯⎯→⎯
+
(2)
The descriptive models could be represented as
algorithmic schemes containing 3 stages: 1) an
image reduction to a recognizable form (an image
model (models) construction); 2) training (adjusting
parameters of chosen algorithms on a training set of
images); 3) recognition (sequential application of
chosen algorithms with adjusted parameters to each
image under recognition). Construction of a multi-
model representation is conceptually the same for
both training set and recognition set; however, as it
will be shown below, training and recognition
process can ramify in stage 1. The latter consists of 2
sub-stages: 1(a) - construction of a multi-model
representation for training set; 1(b) construction of a
multi-model representation for recognition set. In
accordance with chosen recognition algorithms the
sub-stage 1(b) is executed together with sub-stage
1(a) (a case of the same multi-model representations
for training and recognition sets), or it is executed
after sub-stage 1(a) (the sub-stage 1(a) defines multi-
model representations for recognition set), or it is
executed after the stage 2. The latter is a case when
recognition algorithm influences the choice of multi-
model representations for a recognition set.
3 DESCRIPTIVE IMAGE
ALGEBRAS
In this section we introduce operands and operations
(and its operational functions) of DIAs and DIGs
necessary for constructing the algebraic model of the
morphological analysis of lymphatic cell nucleuses.
DIA 1 is a set of color images. The operands: a
set U of
{
}
I - a set of images I={{(r(x,y), g(x,y),
b(x,y)), r(x,y), g(x,y), b(x,y)
∈ [0...M-1]}, (x,y) ∈ X},
M=256 - the value of maximal intensity of a color
component, n - a number of initial images, X - a set
of pixels. The operations are algebraic operations of
vector addition module M, vector multiplication
module M and taking an integral positive part of
multiplication module M by an element from the
field of real numbers in each image point: 1)
I
1
+I
2
={{((r
1
(x,y)+r
2
(x,y)) mod M, (g
1
(x,y)+g
2
(x,y))
mod M, (b
1
(x,y)+b
2
(x,y)) mod M), r
1
(x,y), r
2
(x,y),
g
1
(x,y), g
2
(x,y), b
1
(x,y), b
2
(x,y) ∈ [0...M-1]}, (x,y)
∈ X}; 2) I
1
·I
2
={{((r
1
(x,y)·r
2
(x,y)) mod M,
MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE IMAGE ALGEBRAS - Cytological Specimen Case
67

(g
1
(x,y)·g
2
(x,y)) mod M, (b
1
(x,y)·b
2
(x,y)) mod M),
r
1
(x,y), r
2
(x,y), g
1
(x,y), g
2
(x,y), b
1
(x,y), b
2
(x,y) ∈
[0...M-1]}, (x,y)
∈ X}; 3) αI={{([αr(x,y) mod M],
[αg(x,y) mod M], [αb(x,y) mod M]), r(x,y), g(x,y),
b(x,y)
∈ [0...M-1], α ∈ R}, (x,y) ∈ X}. DIA 1 is
applied to describe initial images and the
multiplication operation of
DIA 1 is applied to
describe segmentation of diagnostically important
nucleus on images.
DIG 1 is a set of operations sb((U,C)
→ U') for
obtaining a binary mask corresponding to an
indicated lymphocyte cell nuclei, C - the information
about the contours of indicated nucleus, a set U' - a
subset of a set U. If an image point (x,y) belongs to
indicated nuclei then r(x,y)=g(x,y)=b(x,y)=1, if a
point (x,y) belongs to nuclei background,
r(x,y)=g(x,y)=b(x,y)=0. The operands: Elements of
DIG 1 are operations sb((U,C)
→ U') ∈ B. The
operations of addition and multiplication are
introduced on the set of functions sb as sequential
operations for obtaining a binary masks and their
addition and multiplication correspondingly: 1)
sb
1
(I,C)+sb
2
(I,C)=B
1
+B
2
; 2) sb
1
(I,C)·sb
2
(I,C)=B
1
·B
2
.
DIG 1 is applied to describe a segmentation process.
DIG 2 is a set U' of binary masks. The
operands:
Elements of DIG2 are binary masks
B={{(r(x,y), g(x,y), b(x,y)), r(x,y), g(x,y), b(x,y)
∈
{0,1}, r(x,y)=g(x,y)=b(x,y)]}, (x,y)
∈ X}, M=256}.
The operations of addition and multiplication are
operations of union and intersection
correspondingly: 1) B
1
+B
2
={{(r
1
(x,y) ∨ r
2
(x,y),
g
1
(x,y) ∨ g
2
(x,y), b
1
(x,y) ∨ b
2
(x,y)), r
1
(x,y), r
2
(x,y),
g
1
(x,y), g
2
(x,y), b
1
(x,y), b
2
(x,y) ∈ {0,1}}, (x,y) ∈ X};
2) B
1
·B
2
={{(r
1
(x,y) ∧ r
2
(x,y), g
1
(x,y) ∧ g
2
(x,y),
b
1
(x,y) ∧ b
2
(x,y)), r
1
(x,y), r
2
(x,y), g
1
(x,y), g
2
(x,y),
b
1
(x,y), b
2
(x,y) ∈ {0,1}}, (x,y) ∈ X}. DIG 2 is applied
to describe binary masks.
DIA 2 is a set of gray scale images. The
operands: A set V of {J} – a set of images J=
{{gray(x,y)}
(x,y) ∈ X
, (x,y) ∈ [0,...,M-1]}. The
operations are algebraic operations of gray
functions addition module M, multiplication module
M and taking an integral positive part of
multiplication module M by an element from the
field of real numbers in each image point: 1)
J
1
+J
2
={{(gray
1
(x,y)+gray
2
(x,y)) mod M, gray
1
(x,y),
gray
2
(x,y) ∈ [0..M-1]}, (x,y) ∈ X}; 2)
J
1
·J
2
={{(gray
1
(x,y)·gray
2
(x,y)) mod M, gray
1
(x,y),
gray
2
(x,y) ∈ [0..M-1]}, (x,y) ∈ X}; 3) αJ={{[α
gray(x,y) mod M], gray(x,y)
∈ [0..M-1], α ∈ R}, (x,y)
∈ X}. DIA 2 is applied to describe separated nucleus
on images.
DIA 3 – a set F of operations f(U
→ V) converting
elements from a set of color images into elements of
a set of gray scale images. The operands: elements
of DIA 3 - operations f(U
→ V) ∈ F; such transforms
can be used for elimination luminance and color
differences of images. The operations of addition,
multiplication and multiplication by an element from
the field of real numbers are introduced on the set of
functions f as sequential operations of obtaining gray
scale images and their addition, multiplication and
multiplication by an element from the field of real
numbers correspondingly: 1) f
1
(I)+f
2
(I)=J
1
+J
2
; 2)
f
1
(I)·f
2
(I)=J
1
·J
2
; 3) αf(I)= αJ. DIA 3 is applied to
eliminate luminance and color differences of images.
DIA 4 - a set G of operations g(V
→ P
1
) for
calculation of a gray scale image features. The
operands: DIA 4 - a ring of functions g(V
→ P
1
) ∈ G,
P
1
- a set of P-models (parametric models). The
operations. Operations of addition, multiplication
and multiplication by a field element are introduced
on a set of functions g as operations of sequential
calculation of corresponding P-models and its
addition, multiplication and multiplication by a field
element. 1) g
1
(J)+g
2
(J)=p
1
(J)+p
2
(J); 2)
g
1
(J)·g
2
(J)=p
1
(J)·p
2
(J); 3) αg(J)= αp(J). DIA 4 is
applied to calculate feature values.
DIA 5 - a set P
1
of P-models. The operands: a
set P
1
of P-models p=(f
1
, f
2
,…,f
n
), f
1,
,f
2
,…,f
n
- gray
scale image features, n - a number of features. The
operations: 1) addition – an operation of unification
of numerical image descriptions: p
1
+p
2
=(f
1
1
,
f
1
2
,…,f
1
n1
)+ (f
2
1
,f
2
2
,…,f
2
n2
)= (f
3
1
,f
3
2
,…,f
3
n3
), n
3
– a
number of features of P-model p
1
plus a number of
features of P-model p
2
minus a number of coincident
features of P-models p
1
; p
2
, {f
3
1
,f
3
2
,…,f
3
n3
} ⊂ {
f
1
1
,f
1
2
,…,f
1
n1
, f
2
1
,f
2
2
,…,f
2
n2
} - different features and
coincident gray scale image features of P-models p
1
and p
2
; 2) multiplication of 2 P-models – an
operation of obtaining a complement of numerical
image descriptions:
p
*
·p
2
=(f
1
1
,f
1
2
,…,f
1
n1
)*(f
2
1
,f
2
2
,…,f
2
n2
)=(f
4
1
,f
4
2
,…,f
4
n4
),
n
4
- a number of significant features of unified P-
model of models p
1
and p
2
, f
4
1
,f
4
2
,…,f
4
n4
- significant
features obtained after analysis of features of P-
model p
1
and P-model p
2
, f
4
1
, f
4
2
,…,f
4
n4
may not
belong to {f
1
1
, f
1
2
,…,f
1
n1
, f
2
1
,f
2
2
,…,f
2
n2
} and may
consist from feature combinations; 3) multiplication
by a field element - operation of multiplication of a
number, a vector, or a matrix by an element of the
field: αp =α(f
1
, f
2
,…,f
n
)=(αf
1
, αf
2
,…, αf
n
). DIA 5 is
applied to select informative features. The addition
is applied for constructing joint parametric image
representation. The multiplication is applied for
reducing a set of image features to a set of
HEALTHINF 2008 - International Conference on Health Informatics
68

significant features. The multiplication by an
element from the field of real numbers is applied for
feature vector normalization.
DIA 6 - a set P
2
of P-models (P
2
includes feature
vectors of the same length). The operands: a set P
2
of P-models p(J)=(f
1
(J),f
2
(J),…,f
n
(J)), n – a number
of features, f
1
(J),f
2
(J),…,f
n
(J) - gray scale image
features, f
1
(J),f
2
(J),…,f
n
(J) ∈ R. The operations of
addition, multiplication and multiplication by a field
element are introduced on the set P
2
as operations of
a vector addition, multiplication and multiplication
by a field element: (1)
p(J
1
)+p(J
2
)=(f
1
(J
1
),f
2
(J
1
),…,f
n
(J
1
))+
(f
1
(J
2
),f
2
(J
2
),…,f
n
(J
2
))=(f
1
(J
1
)+f
1
(J
2
),
f
2
(J
1
)+f
2
(J
2
),…,f
n
(J
1
)+,f
n
(J
2
)); (2)
p(J
1
)*p(J
2
)=(f
1
(J
1
),f
2
(J
1
),…,f
n
(J
1
))*(f
1
(J
2
),f
2
(J
2
),…,f
n
(
J
2
))=(f
1
(J
1
)·f
1
(J
2
), f
2
(J
1
)* f
2
(J
2
),…,f
n
(J
1
)·,f
n
(J
2
)); 3)
αp(J)=α(f
1
(J),f
2
(J),…,f
n
(J))=(α f
1
(J), α f
2
(J),…,α
f
n
(J)). DIA 6 is applied to describe images reduced to
a recognizable form.
Table 1 shows all DIA with one ring and DIG
used for describing the algorithmic scheme for
solving the task of cytological image recognition.
4 AN ALGORITHMIC SCHEME
OF THE MORPHOLOGICAL
ANALYSIS OF THE LYMPHOID
CELL NUCLEUSES
The developed information technology will be
described below and represented by the algorithmic
scheme (2) which is interpreted by means of DIA,
DIM and GDT.
4.1 Initial Data
A database (DB) of specimens of lymphatic tissue
imprints (Fig. 1) was created to select and describe
diagnostically important features of lymphocyte
nuclei images. DB contains 1830 specimens of 43
patients, both specimen images and the contours of
diagnostically important lymphocyte cell nucleus
indicated by experts. The patients belongs to the
following diagnostic groups: aggressive lymphoid
tumors (de novo large and mixed cell lymphomas
(CL), transformed chronic lymphatic leukemia
(TCLL)), innocent tumor (indolent chronic
lymphatic leukemia (CLL)).
Table 1: DIAs with one ring used for describing
algorithmic scheme for solving the task of cytological
image recognition.
Ring elements Ring operations Purpose
DIA1 color images
algebraic operations of
vector addition module
M
, vector multiplication
module M and taking an
integral positive part of
multiplication module
M
by an element from the
field of real numbers in
each image point
description of
initial images
and
segmentation
process
DIG1
operations of
obtaining the
binary mask
corresponds
indicated
lymphocyte
cell nuclei
sequential operations for
obtaining a binary
masks and their addition
and multiplication
description of
segmentation
process
DIG2
binary masks
corresponds
indicated
lymphocyte
cell nuclei
algebraic operations of
union and intersection
description of
binary masks
DIA2
gray scale
images
algebraic operations of
g
ray functions addition
module M,
multiplication module
M and taking an integral
positive part of
multiplication module
M by an element from
the field of real numbers
in each image point
description of
separated
nucleus on
images
DIA3
operations
reducing
color images
to gray scale
images
sequential operations of
obtaining gray scale
images and their
addition, multiplication
and multiplication by an
element from the field
of real numbers
elimination
luminance
and color
differences of
images
DIA4
operations of
image feature
calculation
sequential calculation of
corresponding P
(parametric)-models and
its addition,
multiplication and
multiplication by a field
element
feature
calculation
DIA5 P-models
image algebra
operations (union,
complement,
multiplication by real
number)
selection of
informative
features
DIA6 P-models
operations of a vector
addition, multiplication
and multiplication by a
field element
image
reduction to a
recognizable
form
MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE IMAGE ALGEBRAS - Cytological Specimen Case
69

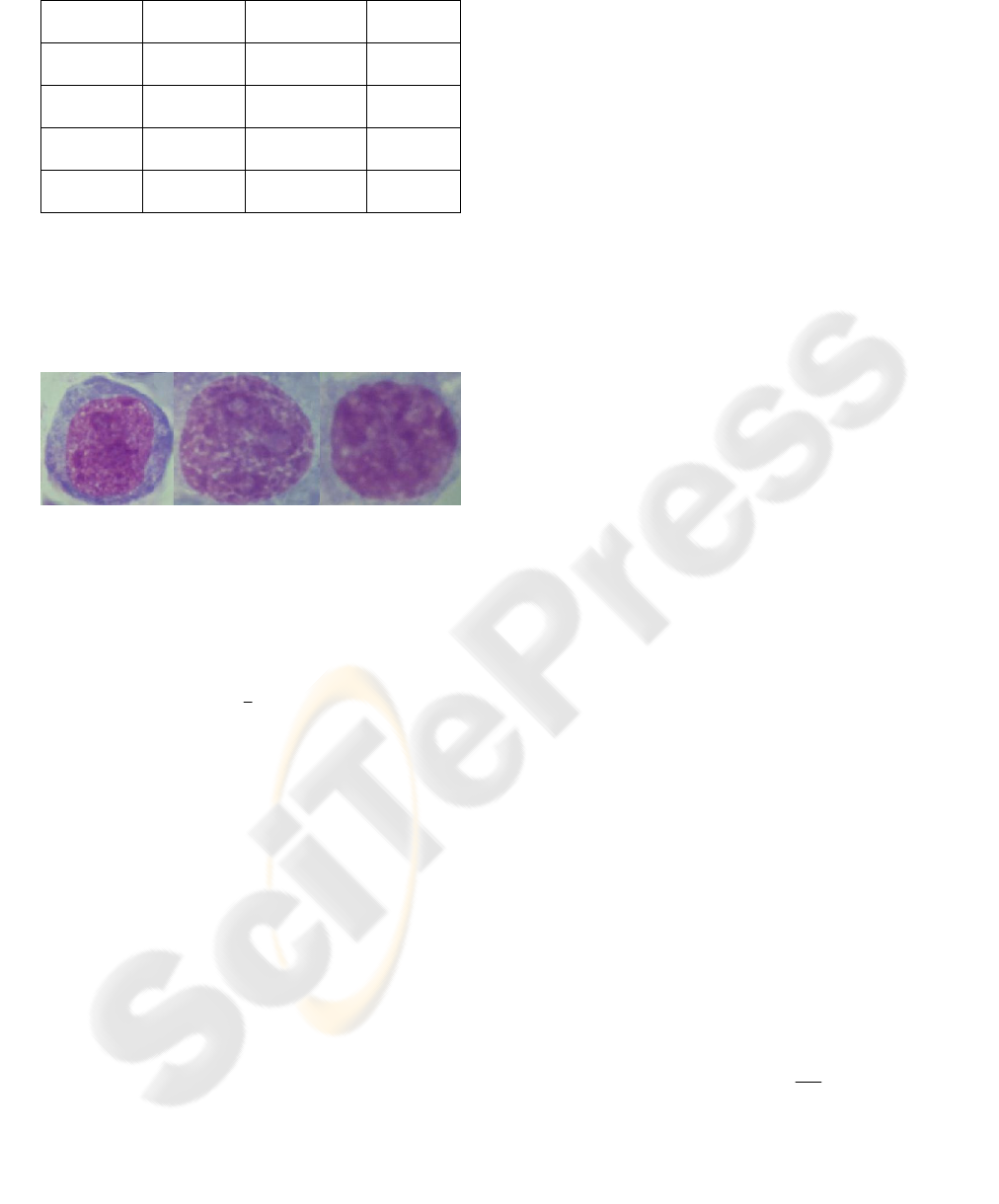
Table 2: Database Statistics.
Diagnosis Patient
number
Image
number
Nuclei
number
CL
18 986 1639
TCLL
12 536 1025
CLL
13 308 2497
Total:
43 1830 5161
Footprints of lymphoid tissues were
Romanovski-Giemsa stained and photographed with
digital camera mounted on Leica DMRB microscope
using PlanApo 100/1.3 objective (Fig. 1). The
equivalent size of a pixel was 0,0036 mcm
2
. 24-bit
color images were stored in TIFF-format.
Figure 1: Specimen nucleus of patients with CL, TCLL
and CLL diagnosis (from left to right).
4.2 Reducing an Image to a
Recognizable Form
The initial images were divided into 2 groups:
training image set
{}
1...
2
n
i
I
⎡⎤
⎢⎥
⎣⎦
and recognition image
set
{}
nn
i
I
...1]2/[ +
. The steps 1.1-1.6 of stage 1
“Reducing an image to a recognizable form”) are
described below as follows: description, step
operands, step operations, results of step operation
applying. It will be highlighted by letters ‘a’ and ‘b’
where processing of training and recognition sets
differs.
Step 1.1: Obtaining Masks of Diagnostically
Important Nucleus on Images. Application of
segmentation algorithm is described by operands
sb((U,C)
→ U') ∈ B of DIG1. An algorithm
sb((U,C)
→ U') ∈ B is applied to initial images in
order to obtain corresponding mask (equation 3).
1
11
1
2
1
1
∈
⎯⎯⎯→
.
...
...
{}
{}
sb DIG
DIA
DIG
j
m
in
B
I
(3)
Step operands are initial images
{}
n
i
I
...1
and
contours of lymphocyte cell nucleus.
Step operation is an operation described by
DIG1. Such description gives flexibility for using
different kind of segmentation algorithms. The
applied algorithm of threshold segmentation was
supplemented by morphological processing of
derivable nuclei images in order to obtain a
corresponding mask.
Results of operation applying are binary masks
1
j
m
B
...
{}
represented as operands of DIG2.
Step 1.2: Segmentation of Diagnostically
Important Nucleus on Images. The mask
multiplication by an initial image gives indicated
nuclei image (equation 4).
1
12
1
1
1
2
11
11
•
≡
⎯⎯⎯→
()
.
...
... ...
{}
( ) ...
{} ,{ }
{(,)}
DIA
DIA
j
m
DIA
in jm
T
I
ij j m
IB
MI B
(4)
Step operands are initial images
{}
n
i
I
...1
and
binary masks represented as operands of DIG2.
Step operation is an operation of multiplication
of 2 operands of DIA1. All initial images were
multiplied by corresponding binary masks.
The results of the operation are
T(transfomatonal)-models
1
1...
{}
j
m
I of initial images.
Step 1.3: Reducing Color Images to Gray Scale
Images. To compensate different illumination
conditions and different colors of stain the specimen
images were processed before feature values
calculation (equation 5).
2
13
1
2
1
3
1
1
1
21
∈
≡
⎯⎯⎯→
.
...
...
{}
...
{}
{()}
fDIA
DIA
j
m
DIA
jm
T
I
jm
I
MI
(5)
Step operands are image models
1
1...
{}
j
m
I .
Step operations are described by the elements of
the DIA 2. Such representation gives flexibility for
using different kinds of processing operations. Here
the function f(U→V)∈F (DIA 2 element) has a form
(I={{(r(x,y),g(x,y),b(x,y)),r(x,y),g(x,y),b(x,y)
∈[0..M-1]}
(x,y) ∈X
}): f(I)=J={{gray(x,y)}
(x,y)∈X
,
(x,y)∈[0...M-1]}, gray(x,y)=g(x,y)
M
B2
, B - an
average brightness of a blue component of an initial
RGB-image. The green tone in this case is the most
informative.
The results of the operation are T-models
2
1...
{}
j
m
I .
HEALTHINF 2008 - International Conference on Health Informatics
70

Step 1.4a: Feature Calculation on Constructed
Image Models of the Training Set. To calculate
different features the training set were processed by
different operations of DIA 4 (equation 6) (m
1
equals to a number of segmented nucleus in training
set).
12
1
4
14
3
11
5
2
1
1
2
11
1
∈
≡
⎯⎯⎯⎯⎯→
{,,...}
.
...
...
{()}
...
{}
{()}
gg DIA
a
DIA
P
m
DIA
jm
P
Mj
jm
I
MI
(6)
Step operands are image models
1
2
1...
{}
j
m
I .
Step operations are described by the elements of
DIA 4. Such representation gives flexibility for
calculation of different features in order to obtain
different P-models
1
P
M
j
() (elements of DIA 5). 47
features were selected for describing each of the
images: the size of nucleus in pixels, 4 statistical
features calculated on the histogram of nucleus
intensity, 16 granulometric and 26 Fourier features
of nucleus.
1
P
M
j
() is the vector with dimension 47
for each image model
2
j
I , j=1...m
1
.
The results of the operation are P-models
1
11...
{()}
P
m
Mj .
Step 1.5a: Selection of Informative Features. This
is an additional step of image model reduction. As it
will be shown below the recognition algorithm was
applied to both a full model
)(
1
jM
P
(j=m
1
+1...m)
and a reduced model
)(
2
jM
P
(j=m
1
+1...m). At this
step the constructed descriptions of images from the
training set are studied for selecting the most
informative features (equation 7).
1
5
15
5
21
6
11
1
21 1
1
+• •
≡
⎯⎯⎯⎯→
(,, )
.
...
...
{()}
...
{()}
{ ( ( ))}
DIA
a
DIA
P
m
DIA
P
m
PP
Mj
m
Mj
MM j
α
(7)
The step operands are image models
1
11...
{()}
P
m
Mj .
Step operations are described by the elements of
DIA 5. Operations of addition and multiplication are
introduced for unificating and for reducing sets of
image features to a set of significant features.
Operation of multiplication by an element from the
field of real numbers is introduced for normalization
of feature vectors. Such representation gives
flexibility for using different kinds of feature
analysis to obtain a reduced set of features.
Application of factor analysis to training image set
detected 14 features with the largest loads in the first
and second factor (Gurevich, 2006).
The results of the operation are P-models
1
21...
{()}
P
m
Mj - a the vector with dimension 14 for
each of image models
2
j
I , j=1...m
1
.
Step 1.6b: Feature Calculation on Constructed
Image Models of the Recognition Set.
The steps
1.4 and 1.5 obtain a multi-model representation for
training set. The step 1.6 is the step of feature values
calculation for a recognition set (equation 8).
12 4
16
6
11
3
22
121 1
1
2
1
1
∈
+
+
≡
⎯⎯⎯⎯⎯→
+
∨
(, ,...)
.
...
...
{()}
...
{() (())}
{}
gg DIA
b
DIA
mm
DIA
PPP
j
jm m
j
jm m
MI MMI
I
Ψ
(8)
Step operands are image models
1
2
1
+ ...
{}
j
mm
I .
Step operations are described by the elements of
DIA 4. To describe each image 47 or 14 features
were selected.
The results of the operation are P-models
11+ ...
{()}
mm
jΨ (note that the multi-model
representation of images was constructed).
4.3 Training and Recognition
The class “Algorithms Based on Estimate
Calculations” (AEC-class) were chosen as
recognition algorithms since they can be
conveniently represented by algebraic tools
(Zhuravlev, 1998).
Initial Data. DIA 6 and its operands
22
121
PPP
jj
j
MI MMI() ( ) ( ( ))Ψ ≡∨ (j=1...m) describe
initial data for recognition algorithm A
(
12 n
j() ( , ,..., )
ψ
ψψ Ψ = - feature vector with a
dimension n=47 or n=14,
11mm
j
..
{()}Ψ
+
- information
about recognition set,
1
1...
{()}
m
jΨ - information about
training set,
11
gj
rxm
gj
rxm
PI a{()} { }
′
=
- information
about memberships of training set images to classes
1...
{}
gr
K ( 01
gi
a {,}
∈
, r=3,
1
′
...
{}
j
m
I - initial
specimen images, one image for each indicated
nucleus). Recognition algorithm
MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE IMAGE ALGEBRAS - Cytological Specimen Case
71

11 1
111 1+−
=∈
.. ... ( ) ...
({ ()} ,{ } ,{ ()} ) { } { }
m
g
rxm m m
g
rx m m
y
l
ii
Aj a j a AΨΨ
solves an image recognition problem,
1...
{}
gj r
a - an
information vector of image model
2
j
I calculated by
algorithm A (j=m
1
+1…m).
The algorithms were applied to both full image
models
)(
1
jM
P
(j=1…m, 47 features) and reduced
image models
)(
2
jM
P
(j=1…m, 14 features).
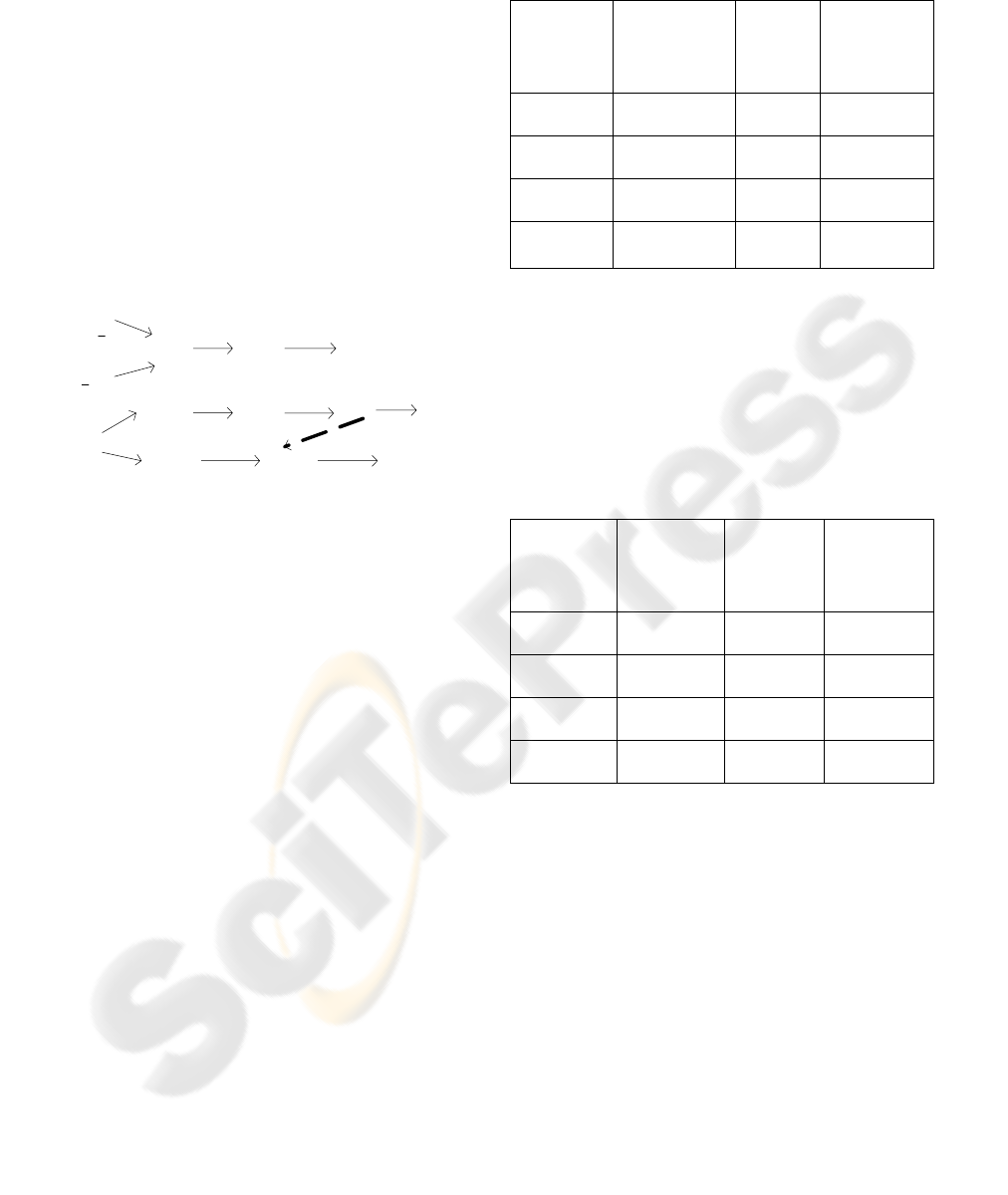
Algorithmic Scheme. We described the main steps
and elements of an algebraic model of information
technology for automation of diagnostic analysis of
cytological specimens of patient with lymphatic
system tumors (Fig. 2):
1
2
⎡⎤
⎢⎥
⎣⎦
...
{}
i
n
I
1
2
⎡⎤
+
⎢⎥
⎣⎦
...
{}
i
n
n
I
1...
{}
j
m
B
1
.
1
a
1
.
1
b
11...
{}
T
j
m
M
21..
{}
T
j
m
M
21..
{}
T
j
m
M
1
11..
{}
P
j
m
M
1
.
4
a
1
.
6
b
1
1+ ..
{}
j
mm
Ψ
1
21..
{}
P
j
m
M
1
{}
gj
rxm
Γ
o
p
1
−
′
()
{}
gj
rx m m
Γ
1.2 1.3
1.5
a
2.1
a
2.2
a
1
−()
{}
gj
rx m m
a
3.1
b
3.2
b
Figure 2: Algorithmic scheme of information technology.
Discussion of the Results. The elements of the
technology were tested via software system
«Recognition 1.0» (Zhuravlev, et al., 2005)
including AEC-algoritms. It appeared that the best
results are achieved by voting using all possible
support sets, while automatic selection of support set
cardinality and selection of support sets of fixed
cardinality give lower precision.
Recognition rate for full feature set (Table 3) is
86,75%, while the rates differ for different
recognition classes. High recognition rate for CLL
(97,84%) is probably connected with innocent nature
of CLL as opposed to CL (63,35%) and
TCLL(84,51%) - the malignant cases. Thus, cells of
CLL have evident distinctions from cells of other
diagnoses, and cells of CL and TCLL are more
similar to each other.
Table 3: The recognition rates for feature description
consisted of 47 features.
Diagnosis
The number
of correctly
recognized
cells
Total
number
of cells
The
recognition
rate
CL
693 820 84,51%
TCLL
325 513 63,35%
CLL
1221 1248 97,84%
Total cell
set
2239 2581 86,75%
The recognition rate reduced feature set (14
features) decreased to 83,18% (Table 4). This
feature set includes following features: size of
nucleus in pixels, average by intensity histogram
(statistic feature), numbers of elements with typical
and minimal size of nuclei (granulometric features),
9 Fourier-features of nucleus.
Table 4: The recognition rates using reduced feature
description consisted of 14 features.
Diagnosis
The number
of correctly
recognized
cells
Total
number of
cells
The
recognition
rate
CL
626 820 76,34%
TCLL
300 513 58,48%
CLL
1221 1248 97,84%
F
ull cell set
2147 2581 83,18%
The software system «Recognition 1.0»
(Zhuravlev, 2005), used for experimental
investigation, includes effective realization of AEC
methods and allows to apply them for practical task
solution. It was experimentally verified that the best
results are achieved by voting using all possible
support sets, while automatic definition of support
set capacity and definition of fixed support set
capacity give lower precision.
5 CONCLUSIONS
The paper demonstrates practical application of
algebraic tools of the Descriptive Approach to Image
Analysis - it is shown how to construct a model of a
technology for automation of diagnostic analysis on
HEALTHINF 2008 - International Conference on Health Informatics
72

images using. It is presented an algorithmic scheme
of a technology implementing the apparatus of DIA.
The paper solves a dual task: it presents technology
by well structured mathematic model it shows how
DIA can be used in image analysis application. The
described techniques and tools will be used for
creating software implementation of the
technologies, its testing and performance evaluation.
ACKNOWLEDGEMENTS
This work was partially supported by the Russian
Foundation for Basic Research Grants Nos. 05-01-
00784, 06-01-81009, 07-07-13545, by Collaborative
project “Image Analysis and Synthesis: Theoretical
Foundations and Prototypical Applications in
Medical Imaging” within agreement between CNR
(Italy) and the RAS, by the project “Descriptive
Algebras with one ring over image models” of the
Program of Basic Research “Algebraic and
Combinatorial Techniques of Mathematical
Cybernetics” of the Department of Mathematical
Sciences of the RAS, by the project no. 2.14 of the
Program of the Presidium of the Russian Academy
of Sciences “Fundamental Problems of Computer
Science and Information Technologies”.
REFERENCES
Gurevich, I.B., 2005. The Descriptive Approach to Image
Analysis. Current State and Prospects. In Proceedings,
14
th
Scandinavian Conference on Image Analysis.
LNCS 3540, Springer-Verlag, Berlin Heidelberg.-
P.214-223.
Gurevich, I., Harazishvili, D., Jernova, I., et al, 2003.
Information Technology for the Morphological
Analysis of the Lymphoid Cell Nuclei. In
Proceedings, The 13
th
Scandinavian Conference on
Image Analysis. LNCS 2749.-P.541-548.
Gurevich, I., Koryabkina, I., Yashina, V., Niemann, H.,
and Salvetti, O., 2007. An application of a Descriptive
Image Algebra for Diagnostic Analysis of Cytological
Specimens. An Algebraic Model and Experimental
Study. In Proceedings, The 2th International
Conference on Computer Vision Theory and
Applications, VISAPP 2007. Volume Special Sessions,
INSTICC Press.-P. 230-237
Gurevich, I., Harazishvili, D.V. Salvetti, O., et al, 2006.
Elements of Information Technology for Cytological
Specimen Image Analysis: Taxonomy and Factor
Analysis. In Pattern Recognition and Image Analysis:
Advances in Mathematical Theory and Applications.
Vol.16, No.1, Pleiades Publishing, Inc. 1. -P. 113-115
Zhuravlev, Yu.I., 1998. An Algebraic Approach to
Recognition and Classification Problems. In Pattern
Recognition and Image Analysis: Advances in
Mathematical Theory and Applications, Vol.8. MAIK
"Nauka/Interperiodica".-P.59-100.
Zhuravlev, Yu.I., Ryazanov, V.V., and others, 2005.
RECOGNITION: A Universal Software System for
Recognition, Data Mining, and Forecasting. In Pattern
Recognition and Image Analysis, Vol. 15, No. 2.
Pleiades Publishing, Inc.-P.476-478.
MEDICAL IMAGE MINING ON THE BASE OF DESCRIPTIVE IMAGE ALGEBRAS - Cytological Specimen Case
73