Extending Morphological Signatures

for Visual Pattern Recognition

Sébastien Lefèvre

LSIIT, CNRS / University Louis Pasteur - Strasbourg I

Parc d’Innovation, Bvd Brant, BP 10413

67412 Illkirch Cedex, France

Abstract. Morphological signatures are powerful descriptions of the image con-

tent which are based on the framework of mathematical morphology. These sig-

natures can be computed on a global or local scale: they are called pattern spectra

(or granulometries and antigranulometries) when measured on the complete im-

ages and morphological proﬁles when related to single pixels. Their goal is to

measure shape distribution instead of intensity distribution, thus they can be con-

sidered as a relevant alternative to classical intensity histograms, in the context of

visual pattern recognition.

A morphological signature (either a pattern spectrum or a morphological proﬁle)

is deﬁned as a series of morphological operations (namely openings and closings)

considering a predeﬁned pattern called structuring element. Even if it can be used

directly to solve various pattern recognition problems related to image data, the

simple deﬁnitions given in the binary and grayscale cases limit its usefulness in

many applications.

In this paper, we introduce several 2-D extensions to the classical 1-D morpho-

logical signature. More precisely, we elaborate morphological signatures which

try to gather more image information and do not only include a dimension related

to the object size, but also consider on a second dimension a complementary

information relative to size, intensity or spectral information. Each of the 2-D

morphological signature proposed in this paper can be deﬁned either on a global

or local scale and for a particular kind of images among the most commonly ones

(binary, grayscale or multispectral images). We also illustrate these signatures by

several real-life applications related to object recognition and remote sensing.

1 Introduction

When applied on visual information such as digital images, pattern recognition and data

mining techniques are very dependent on the accuracy of the image features they rely

on. The image analysis and processing community has proposed from several decades

a large variety of features to represent precisely the content of an image. The features

which have received the most attention from the image scientists and engineers are

context-independent, i.e. they can be used for a various panel of problems and a wide

range of images.

Among these features, the histogram is certainly the most plebiscited and represents

the probability density function of the intensity values in the image. It can be analysed

Lefèvre S. (2007).

Extending Morphological Signatures for Visual Pattern Recognition.

In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 79-88

DOI: 10.5220/0002432700790088

 SciTePress

through various measures such as moments, entropy, uniformity, or other information

criteria. However it does not take into account the spatial relationships between pixels.

On the contrary, approaches such as pattern spectra, granulometries, or morpholog-

ical proﬁles are built from series of morphological ﬁltering operations and thus involve

a spatial information. They can be applied either on a local scale or a global scale. In

the ﬁrst case, the differential morphological proﬁles introduced in [1] have shown their

interest to deal with classiﬁcation of remote sensing data. On a global scale, pattern

spectra and granulometries are widely known in the image analysis community [2].

However all these morphological measures are limited to a single evolution curve and

so cannot consider simultaneously several dimensions. Some attempts have been made

to generate vectorial granulometries [3] or vectorial covariances [4], but they are more

vectorial extensions than multidimensional extensions.

In this paper, we propose several extensions to build 2-D series of morphological

measures. We ﬁrst give the necessary deﬁnitions and show the similarity between the

different morphological measures which have been proposed in the literature. We then

introduce three different 2-D signatures, related to size-size, size-intensity, and size-

spectrum information. The interest of our contribution is then illustrated by several

applications related to object recognition and remote sensing. We believe however that

these extensions can be used as appropriate image features to solve a larger panel of

pattern recognition and image mining problems.

2 Preliminary Deﬁnitions

Morphological signatures are tools provided by the framework of Mathematical Mor-

phology (MM) and known as pattern spectra (and granulometries / antigranulometries)

or morphological proﬁles when computed on a global or a local scale respectively. The

theory of MM has been introduced by Matheron and Serra [5] in the mid sixties and

has been extensively used for 40 years particulary for spatial-based image analysis. The

theoretical framework of complete lattices [6] is commonly used to elaborate morpho-

logical operators on monovalued (binary or grayscale) images. Multivalued (colour or

multispectral) images require the choice of a speciﬁc vectorial ordering [7]. In this sec-

tion, we will recall the deﬁnitions of the basic morphological operators from which we

can then give the formulation of the morphological signature.

2.1 Fundamental Operators

Let f : E → T represents the image to be morphologically processed, with E being

the discrete coordinate grid (usually N

for a 2-D image) while T represents the set

of possible image values. In the case of a binary image, T = {0, 1} where the objects

and the background are respectively represented by values equal to 1 and 0. In the case

of a grayscale image, T is generally a subset of Z, for instance [0, 255]. Finally, Z

is considered for T in case of multispectral images. Most of the available operators

within the MM framework are applied on an input image f (either binary, grayscale

or multispectral) and rely also on a predeﬁned matching pattern B, called structuring

element (SE). In this paper we assume that only ﬂat structuring elements are involved,

thus resulting in the deﬁnition of B as a subset of E.

Based on these notations, the deﬁnitions of the two basic morphological operators

(namely dilation and erosion) are given by:

(f)(x, y) =

(r,s)∈B

f(x − r, y − s), (x, y) ∈ E (1)



(f)(x, y) =

(r,s)∈B

f(x + r, y + s), (x, y) ∈ E (2)

In other words, the dilation δ

(f) results in an image where each pixel (x, y) is associ-

ated to the local maximum of f in the neighbourhood deﬁned by the SE B. The erosion

is the dual operator, considering the local minimum instead of the local maximum.

We can then derive the opening and closing operators:

(f) = δ

(

(f)) (3)

(f) = 

(δ

(f)) (4)

where the two fundamental operators are applied successively to ﬁlter the input image:

erosion followed by dilation for the opening, dilation followed by erosion for the clos-

ing operator, thus resulting in a removal of either local maxima or minima. From these

deﬁnitions we can observe that the strength of an opening or closing ﬁlter depends di-

rectly on the size of the SE B: considering an increasing size λ for the SE, the openings

and closings φ

will remove more and more details from the input image. Indeed the

opening and closing operators ensure respectively the extensivity and anti-extensivity

properties, in other words γ(f ) ⊂ f and f ⊂ φ(f). For the sake of conciseness, we

will use the operator ψ to represent either γ or φ, i.e. the opening or closing operation.

2.2 Morphological Signatures

As indicated earlier in this paper, the morphological signature can be computed either

on a local (i.e. pixel-related) or a global (i.e. image-related) scale, thus resulting in oper-

ators respectively known as morphological proﬁle and pattern spectrum (or granulome-

try / antigranulometry). In order to give the formulation of these different operators, let

us write Π

(f) the series obtained from successive openings or closings:

(f) = {Π

(f) | Π

(f) = ψ

(f), ∀λ ∈ {0, . . . , n}} (5)

where ψ

(f) = f and λ denotes the size of the SE B. We assume either ψ = γ or

ψ = φ. More meaningful series ∆

(f) can be generated with differential measures:

∆

(f) =



∆

(f) | ∆

(f) = Π

(f) − Π

λ−1

(f), ∀λ ∈ {1, . . . , n}



(6)

Finally we can group together opening and closing series to generate a single Π or ∆

series of length 2n:

Π(f) =

(

(f) | Π

(f) =

(

−c

(f), ∀c ∈ {−n, . . . , −1}

(f), ∀c ∈ {1, . . . , n}

)

(7)

∆(f) =

(

∆

(f) | ∆

(f) =

(

∆

−c

(f), ∀c ∈ {−n, . . . , −1}

∆

(f), ∀c ∈ {1, . . . , n}

)

(8)

The morphological signatures widely used in image analysis and visual pattern

recognition can be deﬁned from these different image series, either on a local or a global

scale. In the former case, the morphological proﬁle and the well-known differential

morphological proﬁle (DMP) are respectively deﬁned as Π(f)(x, y) and ∆(f)(x, y)

for a given pixel (x, y) in f . In the latter case, the pattern spectrum is built from

an analysis of the image series Π(f) gathering most frequently the image pixel val-

ues through the volume or sum operation, i.e.

(x,y)∈E

Π(f)(x, y). In the particular

case of binary images, the image volume can either be computed as the sum of pixel

values or as the amount of white pixels (or 1-pixels). Granulometries and antigranu-

lometries are built similarly but are limited respectively to openings and closings, i.e.

(x,y)∈E

(f)(x, y) and

(x,y)∈E

(f)(x, y). As for local signatures, the original

series Π is often replaced in practice by its differential version ∆. Moreover, in order to

obtain a shape probability distribution function, a normalisation may be involved, each

term being then divided by the initial volume

(x,y)∈E

f(x, y).

We will now present several 2-D extensions to the principle of morphological sig-

nature, using the notations introduced in this section.

3 2-D Morphological Signatures

We have seen previously that the well-known (differential) morphological proﬁle and

pattern spectrum (or granulometry / antigranulometry) operators may be written as 1-

D morphological signatures computed on a local or global scale. Here we will present

several 2-D extensions to these signatures, in order to gather more information related

either to size, intensity, or spectral information.

3.1 Size-size Signature

In the Π and ∆ series, a unique parameter λ is considered for measuring the size evo-

lution. In other words, the resulting series are generated by applying openings and clos-

ings with SE B

of increasing size λ. The SE B

for a given size λ can be obtained by

dilating λ times the original SE B using a given SE S:

= {B

| B

= δ

i−1

), ∀i ∈ {2, . . . , λ}}

(9)

with B

= B. The SE S can be chosen either as a simple SE such as a square, a cross,

or a disc of small size (3 × 3 pixels for instance), or as B itself.

This deﬁnition assuming a single size parameter λ prevents us from performing

accurate measurement. Indeed, it is not adequate to elliptical or rectangular shapes for

instance, where the two independent axes should be taken into account.

So we introduce the 2-D size-size signature which is built using SE B

α,β

with two

different size parameters α and β that vary independently. The SE B

α,β

for a given pair

(α, β) of size parameters is obtained by dilating α and β times the original SE B with

two SE S and T :

α,β

= {B

i,j

| B

i,j

= δ

i−1,j

), B

i,j

= δ

i,j−1

), ∀i∀j ∈ {2, . . . , λ}}

α,β

(10)

with B

1,1

= B. A relevant choice for the two SE S and T consists in 1-D SE such as

horizontal and vertical lines respectively, with a length of 3 pixels for instance.

It is then possible to generate the Π series from this 2-D set of SE B

α,β

(f) =



α,β

(f) | Π

α,β

(f) = ψ

α,β

(f), ∀α∀β ∈ {0, . . . , n}



(11)

where the application of ψ on f with a SE B

α,β

is noted ψ

α,β

(f) and with the conven-

tion ψ

0,0

(f) = f. The ∆ series measures the differential in both size dimensions:

∆

(f) =



∆

α,β

(f) | ∆

α,β

(f) =

2Π

α,β

(f) − Π

α−1,β

(f) − Π

α,β−1

(f), ∀α∀β ∈ {1, . . . , n}



(12)

3.2 Size-intensity Signature

As we can notice in the deﬁnitions given in section 2, the pixel intensity values in

grayscale images are used either directly (at local scale) or through the sum operator

(at global scale). The original morphological signature does not take into account the

distribution of intensity values in the image. This can be seen as a strong limitation as

intensity distribution (usually measured by histogram) is a key feature when dealing

with pattern recognition in image data.

So we propose to build at the global scale a 2-D morphological signature which

takes into account both the size and the intensity distributions. To do so, let us use the

Kronecker delta function:

(

1 if i = j

0 if i 6= j

(13)

and the histogram function h

: T → Z:

(θ) =

(x,y)∈E

θf (x,y)

(14)

Alternatively, we can also use the normalised histogram function h

: T → [0, 1] where

(θ) = h

(θ)/

∈T

(θ

). The formulation of the 2-D size-intensity signature is

then given by the following Π series:

(f) =



λ,θ

(f) | Π

λ,θ

(f) = h

(f)

(θ), ∀θ ∈ T, ∀λ ∈ {0, . . . , n}



(15)

and its derivative counterpart is given by the following ∆ series:

∆

(f) =



∆

λ,θ

(f) | ∆

λ,θ

(f) =

(f)−ψ

λ−1

(f)

(θ), ∀θ ∈ T, ∀λ ∈ {1, . . . , n}



(16)

This 2-D size-intensity morphological signature gathers the properties of both the

classical morphological signature and the intensity histogram by considering size and

intensity information together.

3.3 Size-spectrum Signature

We have considered until now that the input image was monovalued. In case of multi-

spectral images where T is equal to Z

or N

, the spectral signature of the image pixels

can be involved into the morphological signature. To do so, it is possible to ﬁrst com-

pute a morphological signature for each of the k spectral components (or bands) and

then to combine these k signatures into a single one, either 1-D or 2-D.

In the case of a 2-D signature, the morphological series Π can be expressed as:

(f) =



λ,ω

(f) | Π

λ,ω

(f) = ψ

), ∀ω ∈ {1, . . . , k} , ∀λ ∈ {0, . . . , n}



(17)

where f

is a grayscale image representing the ω

spectral component of f . In this

deﬁnition the marginal strategy is used, thus the correlation among the different spectral

channels is completely ignored.

To avoid this limitation, it is possible to rather consider a vectorial ordering when

applying the morphological operators γ and φ on the multispectral input image f. The

purpose of a vectorial ordering is to give a way to order vectors and thus to compute

vectorial extrema by means of the two operators sup

and inf

. Assuming a given

vectorial ordering, the fundamental dilation and erosion operators are written:

(f)(x, y) = sup

(r,s)∈B

f(x − r, y − s), (x, y) ∈ E (18)



(f)(x, y) = inf

(r,s)∈B

f(x + r, y + s), (x, y) ∈ E (19)

and from these operators it is possible to write the vectorial versions of the morpholog-

ical opening γ

and closing φ

(f) = δ

(

(f)) (20)

(f) = 

(δ

(f)) (21)

The morphological size-spectrum signature can ﬁnally be expressed as:

(f) =



λ,ω

(f) | Π

λ,ω

(f) = (ψ

(f))

, ∀ω ∈ {1, . . . , k} , ∀λ ∈ {0, . . . , n}



(22)

where (ψ

(f))

= ψ

) in the speciﬁc case of a marginal ordering. For a compre-

hensive review of vectorial orderings and multivariate mathematical morphology, the

reader can refer to [7].

Finally, we can also deﬁne the differential series ∆ as:

∆

(f) =



∆

λ,ω

(f) | ∆

λ,ω

(f) =

λ,ω

(f) − Π

λ−1,ω

(f), ∀ω ∈ {1, . . . , k} , ∀λ ∈ {1, . . . , n}



(23)

We have presented here several 2-D extensions to the classical morphological sig-

nature. We will now show their potential interest when computed either on a local or a

global scale through their use in various applications.

4 Applications

We have presented in the previous section several 2-D extensions to the morphological

signature, which can be computed either on a local or a global scale. The potential

interest of these extensions will be illustrated by a panel of applications made as various

as possible and related to building detection / object recognition / pixel classiﬁcation.

4.1 Building Detection

The 2-D size-size signature has been used as a global scale to determine optimal at-

tributes for image ﬁltering in the context of building detection in panchromatic remote

sensed images. Binary images are obtained by thresholding the initial graylevel images.

The ﬁlter is a morphological opening whose goal is to remove all details smaller than

the estimated size for buildings visible in the binary image.

Figure 1 illustrates the relevance of the proposed 2-D granulometry (using only the

2-D version of the ∆

series) to automatically determine the optimal SE to be used in

the morphological ﬁltering process among sizes (α, β) between (10, 10) and (50, 50).

As we can observe, the proposed SE size (here 19 × 21 pixels, computed as the highest

peak) helps the building detection process by greatly reducing the noisy areas which do

not correspond to buildings. The overall process is given in [8].

Fig. 1. Relevance of the 2-D size-size global signature to determine optimal parameters

for building detection (from left to right and top to bottom): input, unﬁltered and ﬁltered

images, and curve visualisation (the highest peak determines the optimal parameter).

4.2 Object Recognition

In the second application we focus on object recognition in grayscale images. The fea-

ture used is the size-intensity signature which has proven to be more discrimant than

histogram. The experiments were made on the COIL-20 dataset from Columbia Uni-

versity, which contains 1440 images representing 20 objects under 72 viewpoints.

(query #1, histogram) (query #1, proposed) (query #2, histogram) (query #2, proposed)

Fig. 2. Comparison between the 2-D size-intensity global signature and intensity his-

togram for object recognition (the input is the top left image).

Considering only intensity distributions through histograms may result in some mis-

takes between objects, as illustrated by ﬁgure 2. On the contrary, when using morpho-

logical size-intensity signatures of same length, the results are better. This signature also

leads to more symetrical results, thus the two requests #1 and #2 made from a single

viewpoint variation of the same object return as ﬁrst the closest images in the database

(obj3__49.png and obj3__48.png).

Some example objects and their respective 2-D size-intensity signatures are given

in the ﬁgure 3. In this ﬁgure, we have considered a combined Π series of openings and

closings with 256 values for θ and 25 values for λ. We can observe the clear difference

between the signatures of these three objects.

4.3 Pixel Classiﬁcation

The third application illustrates the potential interest of the size-spectrum signature

computed on a local scale to deal with multispectral image interpretation in remote

sensing through pixel classiﬁcation. The image used in this experiment is composed of

1100×900 pixels and 3 spectral components (green, red and near infra-red) and repre-

sents an urban area of Strasbourg, France (ﬁg. 4, left). For each pixel (x, y) we consider

here a 2-D morphological signature ∆ of size 10 × 3 with λ = 5 and ω = 3, i.e. 5

openings and 5 closings for 3 spectral bands. A bayesian classiﬁcation was performed

with 5 classes (buildings, roads, water, vegetation, and shadows). The learning set rep-

resents 1 % of the complete data and 10-fold cross-validation was involved. The overall

accuracy was about 80-85 % with some classes (buildings, 75 %) been worse detected

than others (water, vegetation, shadows, 95 %).

In ﬁgure 4 is given the original multispectral image in false colours and also an

example of classiﬁcation result using this 2-D size-spectrum local signature. More ex-

haustive results can be found in [7].

5 Conclusion

In this paper we have presented several 2-D extensions to the widely used 1-D mor-

phological signature. This signature can be computed on a local or global scale, and

is respectively known as (differential) morphological proﬁle and pattern spectrum (or

granulometry / antigranulometry). We propose to include another dimension related to

size, intensity or spectral information in complement to the initial size distribution, thus

obtaining 2-D size-size, size-intensity, and size-spectrum morphological signatures. We

ﬁnally illustrate the potential interest of these extensions through their use in various

applications: building detection, object recognition, and pixel classiﬁcation.

Future work will include optimisation of the algorithms used to generate the 2-D

signatures in order to reduce the computational cost. Another perspective is to exploit in

a better way the 2-D signatures using matrix computation. We also consider to elaborate

some n-D signatures to gather more information in a single signature. Finally, we will

have to compare the proposed 2-D morphological signatures with well-known non-

morphological measures, such as wavelets or other textures descriptors.

Acknowledgements

The author wish to thank his colleagues Erchan Aptoula and Jonathan Weber for some

of the experimental works made on remote sensing applications.

References

1. Benediktsson, J., Pesaresi, M., Arnason, K.: Classiﬁcation of hyperspectral data from ur-

ban areas based on extended morphological proﬁles. IEEE Transactions on Geoscience and

Remote Sensing 43 (2005) 480–491

2. Soille, P.: Morphological Image Analysis : Principles and Applications. Springer-Verlag,

Berlin (2003)

3. Wilkinson, M.H.F.: Generalized pattern spectra sensitive to spatial information. In: IAPR

International Conference on Pattern Recognition. Volume 1., Quebec City, Canada (2002)

21–24

4. Aptoula, E., Lefèvre, S.: Spatial morphological covariance applied to texture classiﬁcation. In:

International Workshop on Multimedia Content Representation, Classiﬁcation and Security

(IWMRCS), Istanbul, Turkey (2006) 522–529

5. Serra, J.: Image Analysis and Mathematical Morphology. Academic Press (1982)

6. Ronse, C.: Why mathematical morphology needs complete lattices. Signal Processing 21

(1990) 129–154

7. Aptoula, E., Lefèvre, S.: A comparative study on multivariate mathematical morphology.

Pattern Recognition (2007) To appear.

8. Lefèvre, S., Weber, J., Sheeren, D.: Automatic building extraction in vhr images using ad-

vanced morphological operators. In: IEEE/ISPRS Joint Workshop on Remote Sensing and

Data Fusion over Urban Areas, Paris, France (2007)

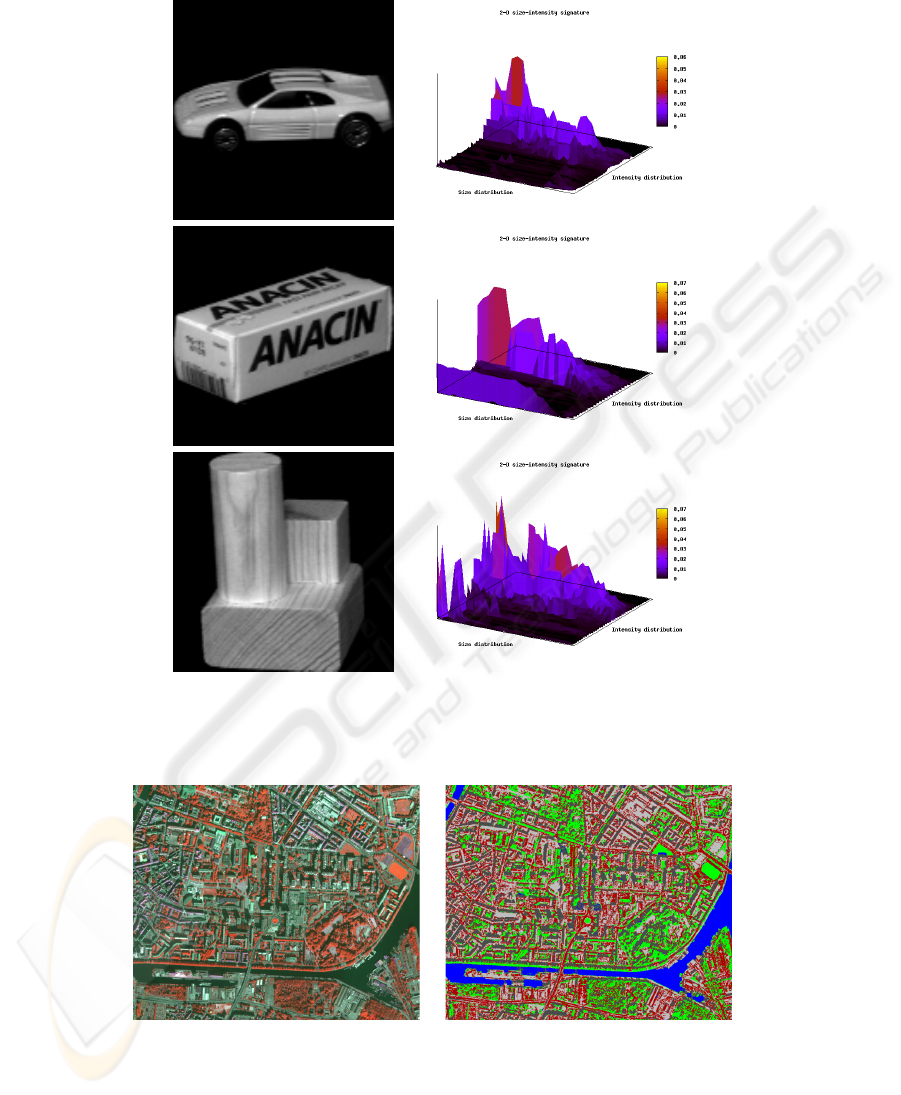
Fig. 3. Relevance of the 2-D size-intensity global signature to discriminate objects in

graylevel images: three different objects (left) with relatively similar histograms and

their respective 2-D signatures (right).

Fig. 4. Relevance of the 2-D size-spectrum local signature to classify pixels in multi-

spectral remote sensed images: input (left) and classiﬁed (right) images.