Automatic Detection of Facial Midline

as a Guide for Facial Feature Extraction

Nozomi Nakao, Wataru Ohyama, Tetsushi Wakabayashi and Fumitaka Kimura

Graduate School of Engineering, Mie University

1577 Kurimamachiya-cho, Tsu-shi, Mie, 5148507, Japan

Abstract. We propose a novel approach for the detection of the facial midline

from a frontal face image. The use of a midline as a guide reduces the compu-

tation time required for facial feature extraction (FFE) because midline is able

to restrict multi-dimensional searching process into one-dimensional search. The

proposed method detects facial midline from the edge image as the symmetry

axis using a new application of the the generalized Hough transformation to de-

tect the symmetry axis. Experimental results on the FERET database indicate that

the proposed algorithm can accurately detect facial midline over many different

scales and rotation. The total computational time for facial feature extraction has

been reduced by a factor of 280 using midline detected by this method.

1 Introduction

Biometrics employing a fully automatic face recognition or authentication technologies

requires both face detection and recognition[1]. In the face detection problem, we are

given an input image that may contain one or more human faces (or it may contain no

face at all). The scale of the face is not known in advance. For example, in a 512 × 768

input image, the face may appear in a small region 64 × 64 size, or it might occupy

the entire range 512 × 768 pixels. The problem is to segment the input image and

isolate the face(s). Particularly, it is necessary to determine a tight bounding box around

each face that contains just the face (forehead to chin), excluding as much of the hair

as possible. Of course, the results of the recognition task[2] depend heavily on how

well the detection task has been done. For example, when the bounding boxes are not

tight enough, Chen et.al[3] showed that non-face artifacts tend to dominate and hence

corrupt the feature extraction process needed for recognition. In this paper we focus on

face detection and localization.

For a human face, there are important features or landmarks that one can exploit

for detection purposes. Although other features can be chosen, we will focus on the

4 most commonly used: center of left eye, center of right eye, tip of nose, and center

of mouth. If the position of these facial features is known, then face detection and

localization can be done easily and more accurately. The detection of facial features,

though, is computationally expensive; hence it makes sense to apply the detection only

in the vicinity of a face and not the entire image (which may contain many non-face

artifacts).

Nakao N., Ohyama W., Wakabayashi T. and Kimura F. (2007).

Automatic Detection of Facial Midline as a Guide for Facial Feature Extraction.

In Proceedings of the 7th International Workshop on Pattern Recognition in Information Systems, pages 119-128

DOI: 10.5220/0002426701190128

 SciTePress

Although the facial features are essential information for the detection of facial

bounding box, the computational cost to detect these features is not negligible. Even

for frontal face images can be recognized as the most simple situation in face recogni-

tion, there are many parameters to estimate, for instance location of each feature, scale

and rotation of faces. If we get any guide that can be utilized for the facial features, by

a method that is easier than that for facial features, it is possible to reduce the computa-

tional cost.

In this paper, we propose a facial midline detector based on generalized Hough

transformation (GHT). This method detects the facial midline from a grayscale image

where one frontal face is. Since faces are often slanted in image, the detection method

must be robust for these varieties. We present an automatic detection technique of the

facial midline and evaluate the performance of the proposed method by experiments

with facial images from the FERET database[4].

In contrary to our method X.Chen et.al.[5] have proposed an automatic method-

ology for the facial midline detection. In their method, axes of facial symmetry are

detected as those which maximize the Y value that is based on the gray level differences

(GLD) between the both sides of the axis. Their approach has the following twofold

drawbacks. (1) the Y value is quite sensitive to change of lighting conditions: if faces

are illuminated from left or right sides, GLD is easily inﬂuenced. (2) It is computa-

tionally expensive because the maximization problem for the Y value is solved by a

sweeping algorithm: in other words, to ﬁnd a axis which maximizes the Y value, we

have to evaluate all combinations of rotation and position of candidates.

The remainder of this paper is organized as follows. In Section 2, we present the

proposed methodology used for face midline detection. Section 3 gives experimental

results and a discussion about the impact of this method is given in Section 4.

2 Proposed Methodology

In this section, we present the proposed methodology for facial midline detection. Our

method is based on bilateral symmetry of human face and extracts the symmetry axis

as the facial midline. To extract the axis reliably, we employ the generalized Hough

transformation (GHT)[6][7] that is able to extract non-analytical curves from an image.

2.1 What is the Facial Midline?

We deﬁne the facial midline as the perpendicular bisector of the interocular line seg-

ment (connecting each eyes). As exampled in Fig.1, when the face in an input image

is slanting with the angle θ, the midline should be detected having the same slanting

angle. Detecting a line on an image is an equivalent problem of detecting one point at

which the line passes and the angle of the line. In Fig.1, the line passing through the

point c = (c

, c

) and the angle θ is expressed as

x − c

sin θ

y − c

cos θ

. (1)

We can determine these two parameters, c and θ, from a pair of points between

which symmetry axis line passes. When two points, p = (p

, p

) and q = (q

, q

), are

120

interocular

line segment

Fig.1. Example of facial midline as the symmetry axis.

symmetrical to each other such that a point c on the axis can be expressed as c =

p+q

And the angle θ is obtained as that is orthogonal to the angle of (q − p). Consequently,

we can rewrite expression (1) using p and q as follows.

x −



+ q



sin θ

y −



+ q



cos θ

, (2)

θ = tan

−1



− p



. (3)

The problem to solve is to extract this pair of symmetrical points, which are given as

examples by p and q in Fig. 1.

We employ the assumption where a frontal face is globally symmetrical. However,

the symmetry of faces is easily corrupted when faces are illuminated form left or right

sides. In this case, to reduce the inﬂuences by illuminations, we have to combine pre-

processes in our method.

2.2 Overview of the Methodology

The proposed method consists of three main stages, as shown in Fig. 2. In the ﬁrst stage,

we apply preprocessing that consists of edge detection, thresholding and noise removal.

The input of the proposed method, which is demonstrated by (a), is a grayscale image

containing one human face in unoccluded frontal view. The size of image is 512 × 768

pixels. And the face is nonrigid and has a high degree of variability in scale, location,

and slant. The resultant image after the preprocessing contains strong edge components

of which lengths are sufﬁcient for the GHT. An example of resultant preprocessed image

is shown in (b). The second stage of this method is the GHT. The GHT requires a proper

reference point for reasonable execution. The reference point is illustrated by p in (b).

The GHT extracts the point that is symmetric to the reference point. The resultant point

is called the relevant point in this research, which is denoted by q in (c). In the third

121

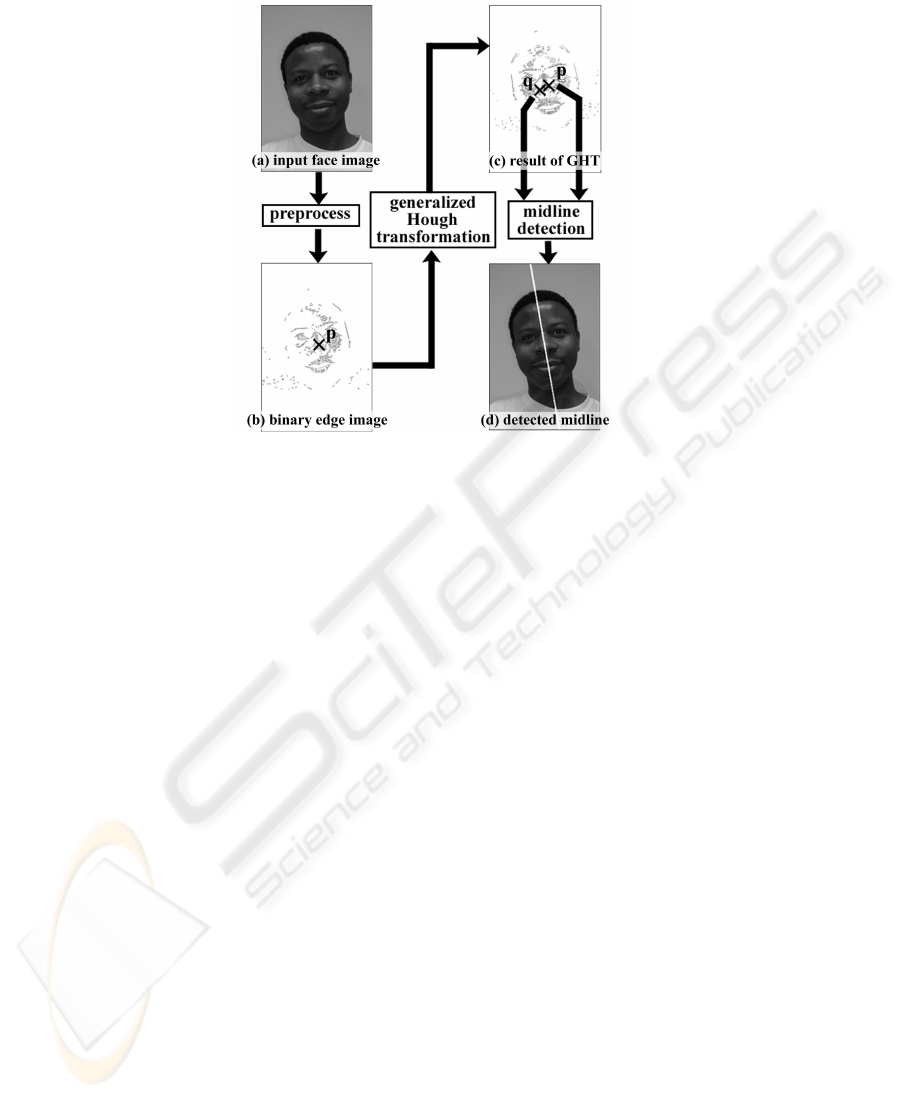
Fig.2. Three main stages of the proposed facial midline detection.

stage, using the detected coordinates of two symmetric points p and q, we obtain the

facial midline by (2).

Brief descriptions of the each process are presented in the following subsections.

2.3 Preprocessing

The preprocessing in the proposed method generates a binary edge image from input

images. Since the GHT algorithm we employ in the second stage is applicable only to

a binary image, it is important to obtain proper binary images for sufﬁcient results. For

instance, the binary image that includes too much noise increases the computational

cost of the GHT and easily corrupts the results mean while the image with too little

edge components makes the reliability of the GHT signiﬁcantly weak.

At ﬁrst, edge magnitude of an input image is calculated by using the Sobel operator.

Edge image is binarized by p-tile thresholding. In this method, a threshold T is selected

as such that p% of the image area has gray values (i.e. edge magnitude) less than T

and the rest has gray values larger than T . Because the Sobel operator enhances noise

in the original image, the resultant binary image might contain some noise if we could

determine the best threshold. To remove the noise, we eliminate edge elements whose

length is smaller than 15 pixels or grater than 800 pixels.

The parameter p for the p-tile thresholding is determined as 91% from preliminary

observation on design data set. The design data set consists of 200 facial images selected

randomly from the FERET database.

122

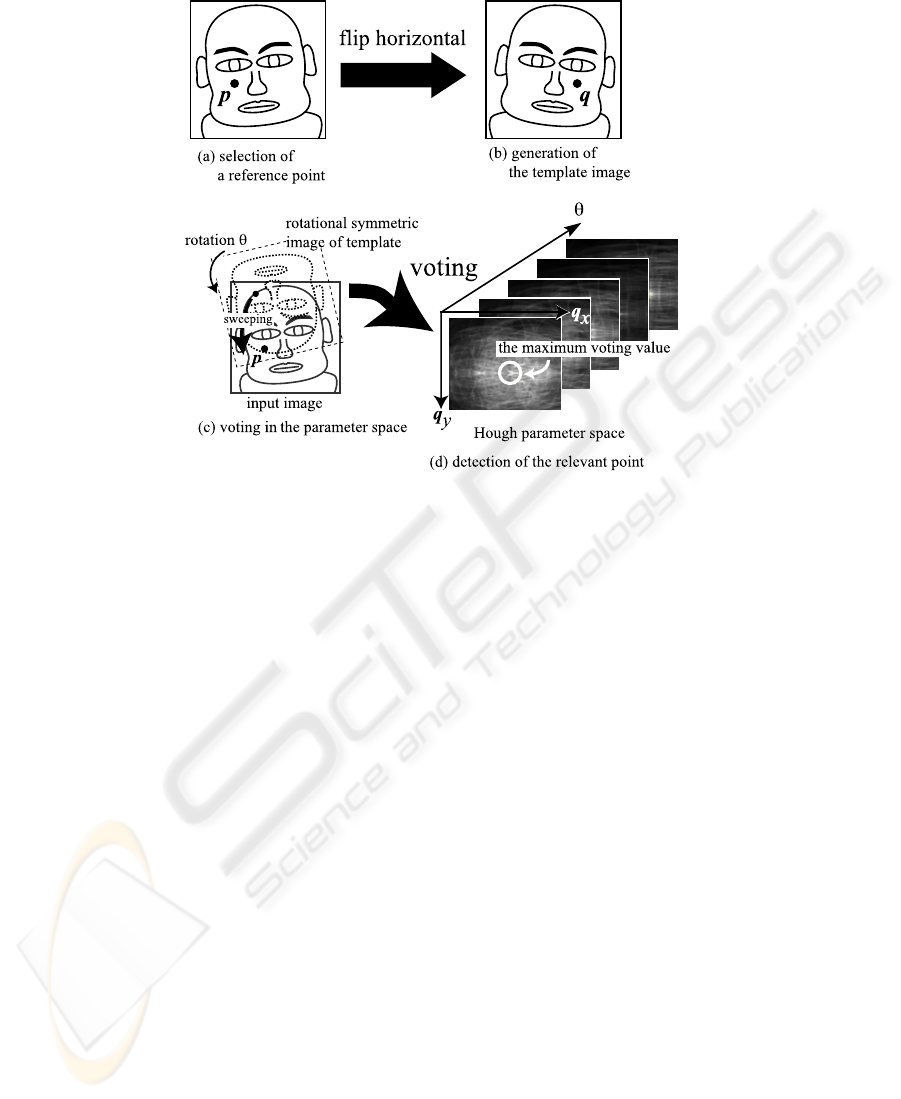
Fig.3. The generalized Hough transformation in the proposed method.

2.4 Generalized Hough Transformation

The generalized Hough transformation (GHT) is an algorithm to detect objects, which

have the same (or similar) shape as a given template, from given binary images. It is

empirically known that GHT is robust to both noise and lack of objects in images.

For binary images, GHT behaves as a fast algorithm of template matching. To adapt

a template to objects in an input image involving variety of poses: scale, position and

rotation, we have to transform and apply the template on the input image by repetition;

hence the computation cost becomes high. To reduce this computational time, GHT

employs voting strategy in a parameter space whose dimensionality is equivalent to the

variety of poses.

The GHT in this research is aimed at ﬁnding the relevant point that is symmetry

to the reference point. The assumption of facial bilateral symmetry suggests that the

edge image might also be symmetric. So we employ the mirror image of the binary

edge image obtained by preprocess as a template. This means that GHT detects the

most similar shape object to the mirror image from the binary edge image. When GHT

detects the object, we can easily detect the pair of symmetry points.

The tasks of GHT in the proposed method are as follows:

(1) Selection of the reference point: For GHT, we should select a reference point in

an image. The selection of the reference point is arbitrary but very important for

reasonable execution because it inﬂuences the performance of the following GHT

steps. It is empirically known that using the centroid as the reference point con-

123

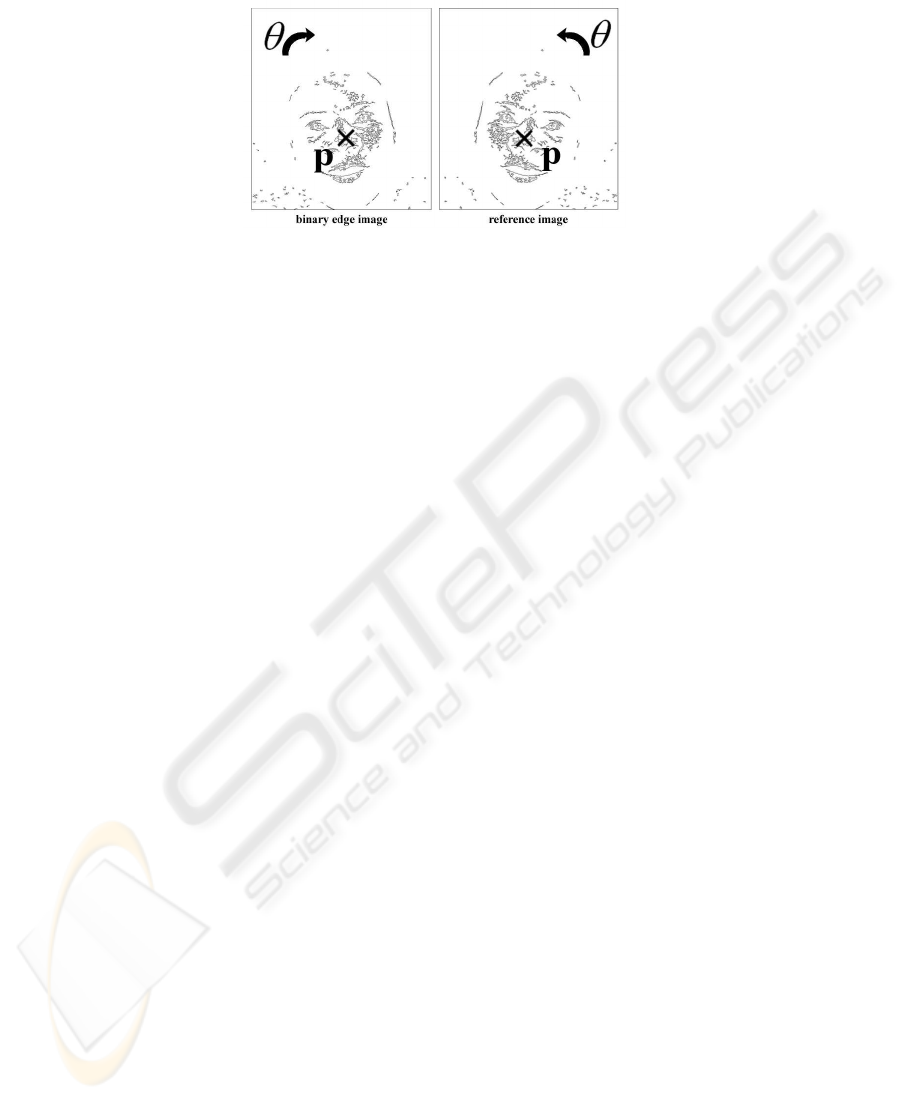
Fig.4. Basic idea of fast midline detection.

tributes to reliable results by GHT. So, we use the centroid of all black pixels (edge

pixels) in the binary edge image as the reference point. An example of the reference

point is shown as p in Fig. 3 (a).

(2) Generation of the template image: As described above, we use the mirror image

of the binary edge image corresponding to the vertical axis as a template. When the

edge image is symmetric corresponding to the vertical axis, the original image and

the template might be overlap considerably at the relevant point (Fig.3(b)).

(3) Voting in the parameter space: The GHT’s parameter space in this method be-

comes three dimensional, i.e. q

, q

and rotation θ. They correspond to the object’s

variety of poses. Fig. 3(c) illustrates the voting process in this method. The sweep-

ing template, which is point symmetric image of the template (b), scans each of all

edge pixels in the binary edge image. During sweeping, the corresponding point in

the parameter space accumulates the vote from the template image.

(4) Detection of the relevant point: The location and the angle of rotation of the tem-

plate are detected from the point in the parameter space, where the maximum voting

value is obtained (Fig. 3(d)).

2.5 Fast Algorithm of GHT

The above tasks provide the proper information to adapt the template to the binary edge

image, though, computational time for these tasks, especially for voting in the three-

dimensional parameter space, is not negligible. To reduce this cost, we introduce the

following restriction for the parameter space.

When a human face displays symmetric corresponding to the vertical axis, in other

words the face is straight in image; the vertical position q

of the template (mirror

image) is exactly same as that of the original binary edge image. If both the reference

and edge images were rotated with the same angle to the opposite direction each other,

the change of q

between the template and the original image is eliminated. This means

that the dimensionalities of the parameter space are restricted to two, q

and θ. Fig. 3

and Fig. 4 illustrates the basic concepts of this method.

Computational time for GHT is signiﬁcantly reduced by this fast algorithm. In our

pilot study, the time for one GHT operation is reduced from 10[s] to 0.06[s].

124

Fig.5. Result of the midline detection.

3 Experiments

To verify the effectiveness of the proposed method, we apply the proposed method to

the images from FERET database. Some examples of detected midline are shown in

Fig. 5. The white line in each picture is the detected midline. The face midline over

many different scales and rotation has detected correctly.

Next, we quantify the performance of the proposed method by evaluation experi-

ment with 2409 frontal face images from the fa and fb probes in FERET database. For

this test, we compare the detected midline with the reference midline obtained from

ground-truth eye locations. As used in [5], two measurements, angle error ∆θ and dis-

tance error s, are used to evaluate the performance of midline detection. The angle

error ∆θ is the difference between detected and reference midlines. The distance error

s is the distance between theses two midlines on the interocular line segment. Fig. 6

illustrates these measures.

Fig. 7 shows the angle error and distance error of the detected midlines for the 2409

images in FERET. 92.74% of the detected midlines are within 5 degrees angle error;

this means that the rotations of face in 92.74% of input images are correctly estimated

by the proposed method. And 75.80% detected distance error are within 10 pixels; this

means that the positions of midline in 75.80% of input images are detected correctly.

These results suggest that the performance of our method is superior than that in [5].

This result suggests that the proposed method provides acceptable performance for

the midline extraction. The computational time of the proposed method for the 2409

facial images is 144.9[s] by a 2.66 GHz Intel Core2 CPU. The frame rate is 16.6

[frames/s].

125

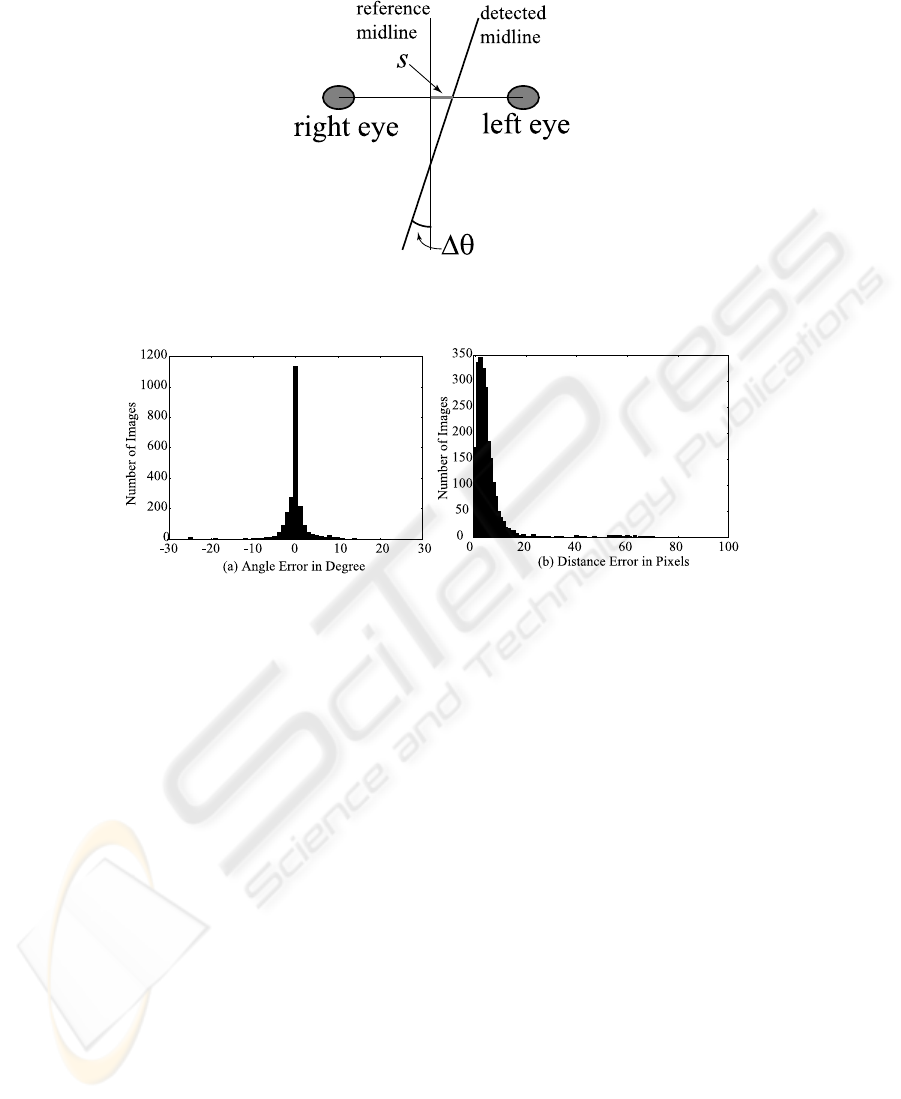
Fig.6. Angle error and distance error for evaluation.

Fig.7. Evaluation results.

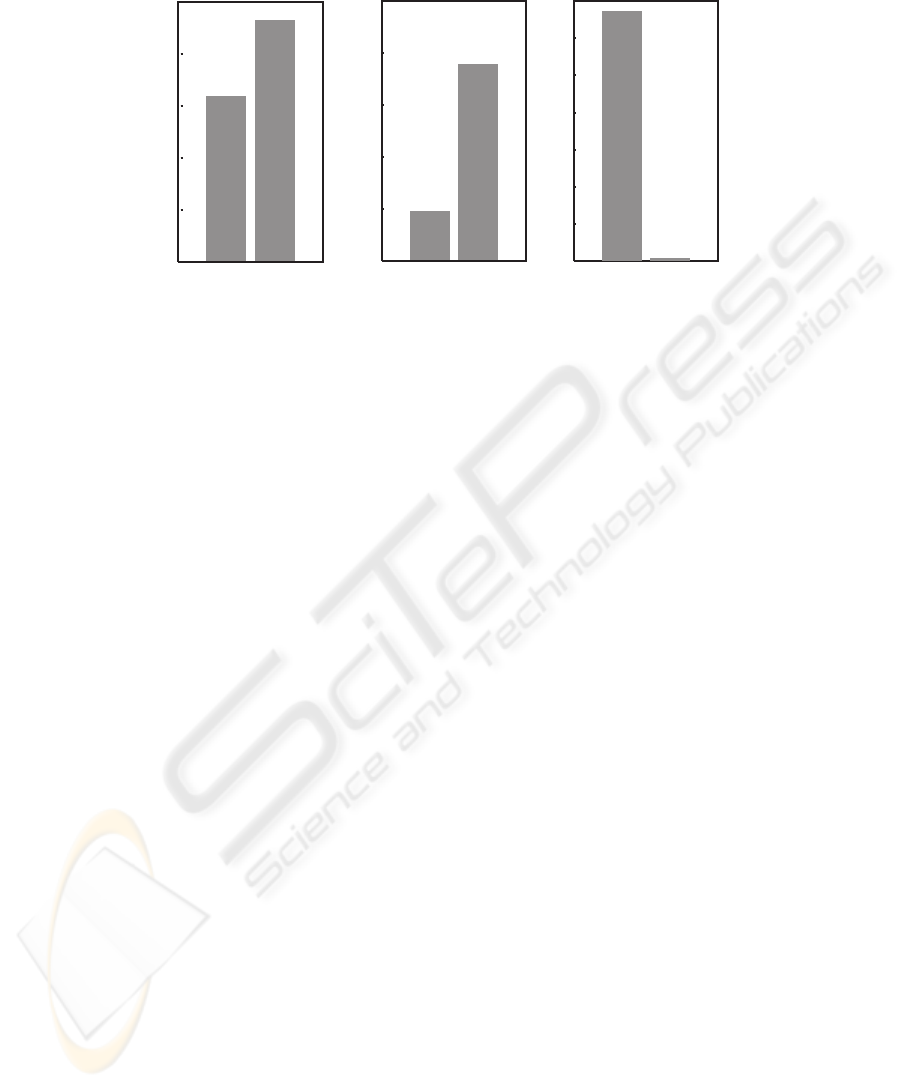
To demonstrate the advantage of our proposed method, we compare the proposed

method and the conventional one, which has been proposed in [5], for the angle and

the distance errors. Fig. 8 (a) and (b) illustrate the comparison of these errors. (a) and

(b) illustrate the number of images where the angle and the distance errors are less than

5 degrees and 10 pixels respectively; in other words, the midline is detected correctly.

These results indicate that the accuracy of midline detection is signiﬁcantly improved

by the proposed method. We also compare these methods for the computational time.

Fig. 8 (c) indicates that the computational time is reduced from 6.7[s] to 0.08[s] for one

input image.

4 Impact of Midline Detection on Facial Feature Extraction

The impact of the proposed method for the facial feature extraction (FFE) is consider-

ably signiﬁcant. Here, we discuss the advantage of the detected midline in FFE.

The use of a midline as a guide for feature extraction reduces the computational

time required for FFE. In FFE, an algorithm must estimate many parameters, which

126

100

proposed

conventional

proposed

conventional

proposed

conventional

% of input image

92.74

63.72

100

% of input image

75.80

19.43

[s]

0.08

6.7

(a) angle error

within 5 degrees

(b) distance error

within 5 degrees

for one input image

Fig.8. Performance comparison between the proposed and the conventional methods.

describe the face, i.e. scale, rotation and position. Midlines which are estimated properly

eliminate these estimation tasks for rotation and reduces the range of position variety.

Fig. 9 shows examples where the detected midlines are used as guide for eye detec-

tion. In this ﬁgure, all eyes are extracted sufﬁciently employing midlines. The proposed

method followed by a simple template matching is employed for the extraction of eyes.

Since we have obtained the rotation angle and the position of the midline before the

template matching, the rotation and parallel shift are corrected preliminary; it makes the

matching method simpler. The comparison of computational time between the methods

with and without the midline detection provides that midline detection reduces the total

computational time from 280 to 1 for the FERET database.

5 Conclusions

In this paper, we propose a detection methodology for the face midline from an image.

Our method based on the GHT is fast, easy to implement and has good performance.

Using detected midlines as a guide for facial feature extraction reduces the computa-

tional cost.

Our future work consists of (1) further improvement of the performance, (2) com-

paring the performance of this method with other methodologies and (3) development

of proper application of the detected midline.

Acknowledgements

Portions of the research in this paper use the FERET database of facial images collected

under the FERET program, sponsored by the DOD Counterdrug Technology Develop-

ment Program Ofﬁce.

127

Fig.9. Results of the facial feature extraction where the midlines are employed as guide for

restriction to the vertical scan-line number of one.

References

1. M.-H. Yang, D. J. Kriegman, and N. Ahuja.: Detecting faces in images: A survey. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence, Vol. 24, No. 1 (2002) 34–58

2. W.Zhao, R.Chellappa, P. Phillips, and A.Rosenfeld.: Face recognition: A literature survey.

ACM Computing Surveys, Vol. 35, No. 4 (2003) 399–458

3. L.-F. Chen, H.-Y. M. Liao, J.-C. Lin, and C.-C. Han.: Why recognition in a statistics-based

face recognition system should be based on the pure face portion: a probabilistic decision-

based proof. Pattern Recognition, Vol. 34, No. 7 (2001) 1393–1403

4. P.J. Phillips, H. Moon, S.A. Rizvi, P. J. Rauss.: The FERET Evaluation Methodology for

Face Recognition Algorithms, IEEE Trans. Pattern Analysis and Machine Intelligence, Vol. 22

(2000) 1090–1104

5. X. Chen, P. J. Flynn, K.W. Bowyer: Fully Automated Facial Symmetry Axis Detection in

Frontal Color Images, 4-th IEEE Workshop on Automatic Identiﬁcation Advanced Technolo-

gies, (2005) 106–111

6. D.H.Ballard.: Generalizing the Hough Transform to Detect Arbitrary Shapes, Pattern Recog-

nition, Vol. 13, No. 2 (1981) 111–122

7. E.R.Davis.: A New Framework for Analysing the Properties of the Generalized Hough Trans-

form, Pattern Recognition Letters, Vol. 6 (1987) 1–7

8. O. Jesorsky, K.J. Kirchberg, and R.W. Frischholz.: Robust Face Detection Using the Hausdorff

Distance, Proc Int’l Conf. Audio- and Video-Based Biometric Person Authentication (2001)

90–95

9. M. Hamouz, J. Kittler, J.-K.Kamarainen, P.Paalanen, H. K

alvi

anen, and J.Mates.: Feature-

Based Afﬁne-Invariant Localization of Faces, IEEE trans. On Pattern Analysis an Machine

Intelligence, Vol. 27, No. 9 (2005) 1490–1495

128