The Role of Intensional and Extensional Interpretation

in Semantic Representations – The Intensional and

Preextensional Layers in MultiNet

Hermann Helbig and Ingo Glöckner

University at Hagen, Intelligent Information and Communication Systems, Germany

Abstract. Although it is well known that the full meaning of a concept includes

an intensional and an extensional aspect, the latter is neglected in almost all prac-

tically used knowledge representations and semantic formalisms, which consider

only the interrelationships between concepts but not their referential meaning. In

logically oriented representations with the usual model-theoretic interpretation,

the extensions of predicates or symbols of the language in general belong to a

metalevel (the model level) clearly distinguished from the logical language. In

this paper, we show in what way the extensional aspect is important (in addition

to the intensional aspect) to account for the full meaning of natural language ex-

pressions. The necessity of dealing with both types of meaning is illustrated by

means of semantic phenomena like factual and intensional negation, intensional

quantiﬁcation and cardinalities, or by the meaning of prepositions describing set

relationships, and others. We will utilize the framework of Multilayered Extended

Semantic Networks (MultiNet) to discuss these issues. The MultiNet formalism

is successfully used in various NLP applications. Its explicit modeling of inten-

sional and preextensional layers offers an explanation of the interplay of inten-

sion and extension of conceptual entities in the overall process of constituting the

meaning representations of natural language expressions.

1 Introduction

At the latest since Carnap, it is well known that the full meaning of a concept is con-

stituted by two aspects, its intension and its extension [1]. The ﬁrst part comprises the

embedding of a concept in the world of concepts as a whole, i.e. the totality of all re-

lations to other concepts. The second part establishes the referential meaning of the

concept, i.e. its counterpart in the real or in a possible world. The intension of the con-

cept Napoleon I, for instance, comprises the relations to the concepts France, emperor,

etc., while its extension is a concrete historical person. The concept emperor again is

related to government, autocracy, etc., while its extension is the set of all emperors of

this world. The aim of this paper is to show the necessity to deal with both aspects in a

knowledge representation and to discuss to what degree this can really be done.

Of course, it is impossible to cope with the full extensions of concepts on a com-

puter, since some concepts have an inﬁnite extension (e.g. successor), some have a

fuzzy extension (e.g. hill, large), and some (like extension) arguably cannot be assigned

Helbig H. and Glöckner I. (2007).

The Role of Intensional and Extensional Interpretation in Semantic Representations – The Intensional and Preextensional Layers in MultiNet.

In Proceedings of the 4th International Workshop on Natural Language Processing and Cognitive Science, pages 92-105

DOI: 10.5220/0002415900920105

 SciTePress

an extension at all. These observations suggest that one should rather incorporate par-

tially described extensions in a KRS

, which represent only typical members or subsets

of the extension of the concept, or only the cardinalities of the corresponding sets. Thus,

we speak of a “preextensional” instead of an “extensional” interpretation. It is postu-

lated that the extensional meaning of a concept has to be modeled in the representational

formalism itself (not outside of it as in logic-oriented KRS with a model-theoretic se-

mantics). The role of intension and extension in the semantic interpretation of linguistic

expressions and even in coreference resolution, is illustrated by the following example:

“(A group of (four men)

[CARD=4]

))

[CARD=1]

found (many gems)

. Six of (them

)

[CARD>6]

had been stolen.”

The example shows the following: Semantically, there is one group of men, not several

groups (as indicated by [CARD=1]), consisting of four men (indicated by [CARD=4]),

who discovered a rather underspeciﬁed set of gems. Nobody would ﬁgure out during

understanding of the ﬁrst sentence how many gems there are (or any other details on the

extension of the concept described by many gems). But, when reading the second sen-

tence, it becomes clear from the partitive construction six of them that the pronoun them

cannot refer to the group of men (since there are only four) but must rather be linked to

the meaning of the phrase many gems, indicated by the index i. Moreover, the preposi-

tion of in the phrase four of them establishes a set inclusion between the extensions of

the conceptual entities denoted by many gems and the stolen objects. It becomes also

clear that the set underlying the intensional meaning of the quantiﬁcationally under-

speciﬁed phrase many gems must have a cardinality greater than 6. All this has to be

modeled in a full meaning representation (see Sect. 2.1); the semantic representation of

an analogous example is shown in Figure 4.

There are few proposals to deal with this extensional dimension besides the inten-

sional aspect in a KRS, one early example is [2]. Elements of the extensional meaning

of concepts are also present in KL-ONE [3] and its successors, i.e. in several kinds of

Description Logics [4]. Here, we meet them in form of the cardinalities of roles. The

aspect of extensionality which traditionally raised most interest is that of characterizing

the real-world existence or facticity of entities mentioned in a discourse. Apart from

the vast literature on presuppositions, this topic has also been addressed in modal logics

[5] and in the context of knowledge representation [6–9].

In the paper, we discuss these issues from the perspective of Multilayered Extended

Semantic Networks (MultiNet), a KRS designed with a clear distinction of an inten-

sional layer and a preextensional layer in mind. The formalism, extensively docu-

mented in [10], is successfully used in large NLP applications, ranging from question

answering over natural language interfaces to electronic teaching (see Sect. 8). After

introducing the core concepts of MultiNet, we turn to the main topic, discussing sev-

eral phenomena of linguistic relevance whose treatment in a KRS calls for a model-

ing on a (pre)extensional level. We address the distinction of intensional quantiﬁcation

vs. preextensional cardinality, the discernment of intensional and preextensional nega-

tion, treatment of existential presuppositions and of implicative or factive verbs, the

modeling of counterfactuals, and the modeling of set relationships implicit in partitive

constructions and quantiﬁcation involving coordinations.

Knowledge Representation System(s)

2 Multilayered Extended Semantic Networks

2.1 The Main Characteristics

In designing a KRS, one should ﬁrst specify a set of criteria to be satisﬁed by the en-

visioned knowledge representation. In our context, the most important of these criteria

are: 1) cognitive adequacy – which to the very least means that the semantic represen-

tation should be concept-centered in the sense that every conceptual entity has a unique

representative; 2) homogeneity – the descriptive means should be suitable for deﬁning

the semantics of lexemes, the semantics of sentences or texts, and the axiomatic appa-

ratus and inference rules of the KRS as well; and 3) stratiﬁcation – it must be possible

to represent the different semantic aspects (like intensional vs. extensional aspects, or

immanent vs. situational aspects of meaning) in different layers of the KRS.

Like other semantic network formalisms, MultiNet represents conceptual entities

by nodes, while relations between concepts are represented as arcs between these nodes

(see Figure 4). However, MultiNet has several additional features:

1. The nodes of the SN are classiﬁed according to a predeﬁned conceptual ontology,

i.e. by a sort assignment.

2. The nodes have a rich inner structure, i.e. the relevant classiﬁcatory dimensions of

conceptual entities are expressed by values of ‘layer attributes’ of each node.

3. The formalism commits to a ﬁxed set of relations in order to provide a stable basis

for axiomatization and a platform for long-term projects like lexicon development.

4. The distinction of an intensional layer and a preextensional layer has already been

mentioned. Each layer comes with its own relations and functions and its own layer

attributes which reﬁne the description of a node at the considered level.

5. We discern categorical knowledge about a concept (e.g. for the concept car: “A car

has a motor”), prototypical knowledge about the concept which only holds by de-

fault (“A car typically has an airbag”) and ﬁnally so-called situational knowledge,

i.e. contingent knowledge about a concept which is irrelevant with respect to the

concept’s core meaning. For example, the introduction of a speciﬁc car in the sen-

tence “Paul bought a car” is situational with respect to the generic concept car and

has no effect on the meaning of car in general.

6. Axiomatic rules (meaning postulates) are employed for interrelating the meanings

of natural language expressions described in the lexicon. They also deﬁne the basic

relations and functions, which can be viewed as nodes at a metalevel.

For a complete documentation of the expressional means of MultiNet see [10].

2.2 Sorts and Features of Concepts

In MultiNet, every node is assigned a sort from a ﬁxed sort hierarchy whose upper part

is shown in Figure 1. The primary purpose of these sorts is that of deﬁning the signatures

(i.e. the domains and value restrictions) of the relations and functions provided by the

formalism. The restrictions imposed by the sorts on the use of relations and functions

or on the valency frames of verbs, nouns, and adjectives are automatically enforced by

the workbenches for the knowledge engineer [11] and for the computer lexicographer

Fig. 1. The Upper Part of the Hierarchy of MultiNet Sorts .

[12], which use MultiNet for representing knowledge and describing lexical semantics.

The sorts are crucial for the formal deﬁnition of the representational means, but also

an important source of information for disambiguation in the semantic interpretation

of linguistic constructs (e.g. prepositional phrases). However, the sorts alone are too

coarse to specify arbitrary selectional restrictions. For that one needs additional seman-

tic features (e.g. being animated or being an artifact) also offered by MultiNet [12].

2.3 Relations and Functions of MultiNet

The formal devices for interlinking the conceptual nodes of a semantic network are

relations and functions. MultiNet provides a ﬁxed set of about 140 semantic relations

and functions which can roughly be classiﬁed into two main groups.

Firstly, there are relations and functions of the intensional level. They are used to

describe the inner structure of conceptual objects and situations as well as their rela-

tionships to other entities. Typical descriptions of objects involve the characterization

of their material structure (by the part-whole-relationship PARS), of their material ori-

gin (described by the ORIGM relation), or of their properties (using the PROP rela-

tion). Situational concepts like events or states, on the other hand, are typically deﬁned

by specifying the participants involved in the situation and the semantic roles which

characterize the relationship between a situation and its participants. Typical examples

are deep case relations like AGT (agent), EXP (experiencer), or OBJ (neutral object).

Additionally, situations are characterized by their spatio-temporal embedding (e.g. lo-

cation LOC or temporal speciﬁcation TEMP). See Table 1 for a brief description of the

relations on the intensional level referenced in this paper.

Second, there are also relations and functions of the preextensional level (see Table

2). They offer the descriptive means needed for modeling sets and other extensional

Table 1. Typical relations of the intensional layer. The notation ¨o requires an entity of sort o with

[ETYPE>0] (i.e. a plurality) while o or si require generic concepts with [GENER=ge].

Relation Signature Short Characteristics

AFF si × [o ∪ si] Affected object

AGT si × co Agent

ANTE [si∪t]×[si ∪t] Temporal successorship

ASSOC ent × ent Association

ATTCH o × o Attachment of objects to objects

AVRT dy × o Aversion/Turning away

CAUS si × si Causality relation

COND si × si Conditional relation

EXP si × o Experiencer

HSIT si × si Composition of situations

LOC co × l Location of an object

MCONT si × [si ∪ o] Mental or informational content

MODL si × md Modal restriction

OBJ si × [o ∪ si] Neutral object

ORIGM co × co Relation of material origin

ORNT si × o Orientation towards something

PARS co × co Part-whole relation for concrete objects

PRED ¨o × o Speciﬁcation of a plurality

POSS o × o Possession

PROP o × p Relation between object and property

SUB o ×

o Conceptual subordination (for objects)

SUBS si × si Conceptual subordination (for situations)

SUBST [o×o]∪[si×si] Substitution/Replacement

TEMP si × [si ∪ t] Relation of temporal containment

representatives. Some rationale for introducing these constructs has already been given

in the introduction and the remainder of the paper will focus on these constructions.

Relations and functions are characterized by implicational axioms familiar from

ﬁrst-order predicate logic. We discern two types of axioms: 1) B-axioms which interre-

late natural language concepts; and 2) R-axioms which connect relations and functions

of the formalism without reference to any lexicalized concept. The connection between

the concepts kill and die is a typical case of a B-axiom:

(sv

SUBS kill) ∧ (sv

AFF o) → ∃sv

[(sv

SUBS die) ∧ (sv

AFF o)]

On the other hand, the relationship between causality and temporal order can be ex-

pressed by an R-axiom (s

CAUS s

) → ¬(s

ANTE s

). For an overview of the dif-

ferent types of axioms used in MultiNet see [13].

2.4 Stratiﬁcation of the Networks

The MultiNet formalism was designed such that qualitatively different aspects of mean-

ing will not be pressed into one ﬂat structure. To this end, the nodes and arcs of MultiNet

are embedded in a multidimensional space of so-called layer attributes. The layer speci-

ﬁcations for arcs are deﬁned by a K-TYPE attribute which assigns one of the knowledge

Table 2. Relations of preextensional layer. p(e)

denotes extensions of entities with [ETYPE=n].

Relation Signature Short Characteristics

*DIFF p(e)

×p(e)

→ p(e)

Set difference (of extensions)

DPND p(e) × p(e) Dependency (of extensions)

ELMT p(e)

× p(e)

n+1

Membership (of extensions)

EXT ent × p(e) Extension

SUBM p(e)

× p(e)

Subsumption (inclusion of extensions)

*UNION p(e)

×p(e)

→ p(e)

Set-theoretic union (of extensions)

types mentioned in point 5, Section 2.1 to each argument of the edge. For nodes, the

layer speciﬁcation comprises a whole set of so-called layer attributes (see Figure 2).

The following layer attributes describe a conceptual entity at the intensional level:

• GENER: The degree of generality indicates whether a conceptual entity is generic

(value: ge) or speciﬁc (value: sp). Example: “A lion [GENER=ge] is dangerous.”

vs. “(This lion) [GENER=sp] is dangerous.”

• QUANT: The intensional quantiﬁcation represents the quantitative aspect of a con-

ceptual entity, i.e. whether it is a singleton (value: one) or a multitude (values: two,

several, many, all etc). Within the set of values characterizing multitudes, we dis-

cern between fuzzy quantiﬁers like several, many, most with value [QUANT=fquant]

and non-fuzzy quantiﬁers like two, three, all with value [QUANT=nfquant]. Exam-

ple: “(Two dogs) [QUANT=nfquant, CARD=2] barked.”

A bundle of four additional layer features is concerned with the extensional aspect:

• ETYPE: This attribute characterizes the type of extensionality of an entity with

values: nil – no extension (e.g. intension), 0 – individual that is not a set (e.g.

Napoleon I ), 1 – entity with a set of elements from type [ETYPE=0] as extension

(e.g. hmany emperorsi, hthe dynastyi), 2 – entity with a set of elements from type

[ETYPE=1] as extension (e.g. hmany dynastiesi), etc.

• FACT: The facticity attribute, to be discussed in greater detail in Section 5, discerns

actually existing objects and situations [FACT=real] from non-existing objects or

situations [FACT=nonreal] and hypothetically assumed objects or situations which

are labeled [FACT=hypo]. Example: “(The girl) [FACT=real] dreamed that (she

was crying) [FACT=hypo].”

• REFER: This attribute speciﬁes the determination of reference, i.e. whether there

is a determined object of reference (value: det) or not (value: indet). The REFER

attribute is especially important for guiding coreference resolution in a discourse

processing or ‘assimilation’ stage which constructs an integral representation of a

whole text from the representations of individual sentences [14].

Example: “(The boy) [REFER=det] bought (a toy) [REFER=indet].”

• CARD: We have already met this cardinality attribute in the introduction. As op-

posed to the intensional quantiﬁcation expressed by QUANT, the CARD attribute

speciﬁes the actual cardinality of the extension of a node.

• VARIA: The variability indicates whether an object is conceptually varying (value:

var) – i.e. it is a ‘parameterized object’ – or if it is a ﬁxed constant (value: con). Ex-

ample: “(The teacher) [VARIA=con] looked at (every homework) [VARIA=var].”

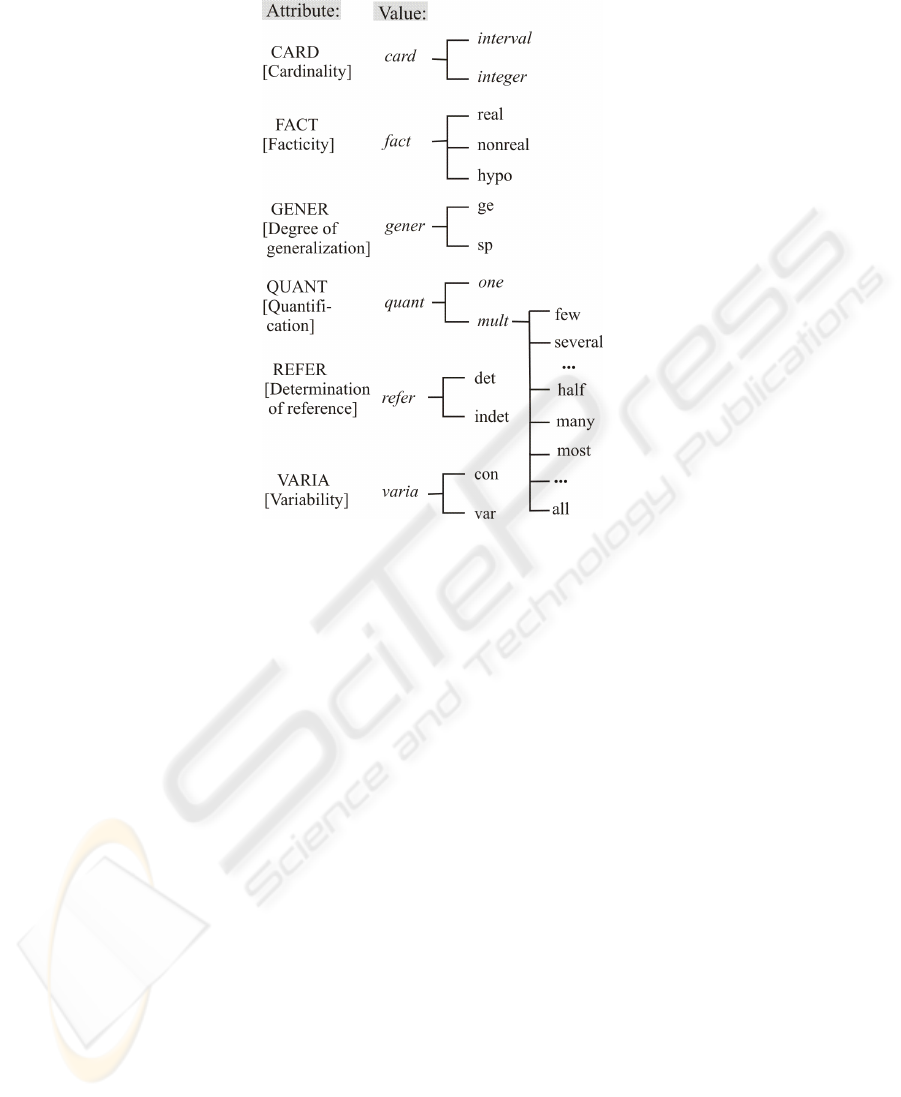
Fig. 2. The multidimensional space of layer attributes.

The idea of layers is motivated by an analogy to the mathematics of an n-dimensional

space. If one ﬁxes a value along one of the axes of an n-dimensional coordinate system,

one gets a (n − 1)-dimensional hyperplane. In the same way, if one is ﬁxing one value

of a layer attribute (let us assume [GENER=ge] or [FACT=hypo]), then one gets a

special layer or stratum (in this case the layer of all generic concepts or the layer of

all hypothetical entities, respectively). The interplay of these layer attributes becomes

visible in the representations of the following two sentences (see Figure 3):

(E1) “All students own bicycles.” (E2) “Every student owns a bicycle.”

In Figure 3, the ﬁrst statement is represented by the POSS arc labeled with (1) and

the second by the POSS arc labeled with (2). As shown in the ﬁgure, the extension of

node n

(representing the concept hevery studenti) is a varying individual p

within the

set p

of all students. The abbreviations hall i and heveryi stand for a whole bundle of

layer attributes and their values shown in Table 3. [ETYPE=+k] in this table means that

the extension type of a concept characterized with every/all is incremented by k com-

pared to the ETYPE of the basic concept found in the lexicon. The counterpart p

at the

preextensional level of node n

at the intensional level (a varying, parameterized, and

individual bicycle) is connected by the dependency relation DPND with the extensional

representative p

of n

. This, together with the layer information of n

, gives a special

reading to sentence (E2) saying that every single student owns exactly one bicycle de-

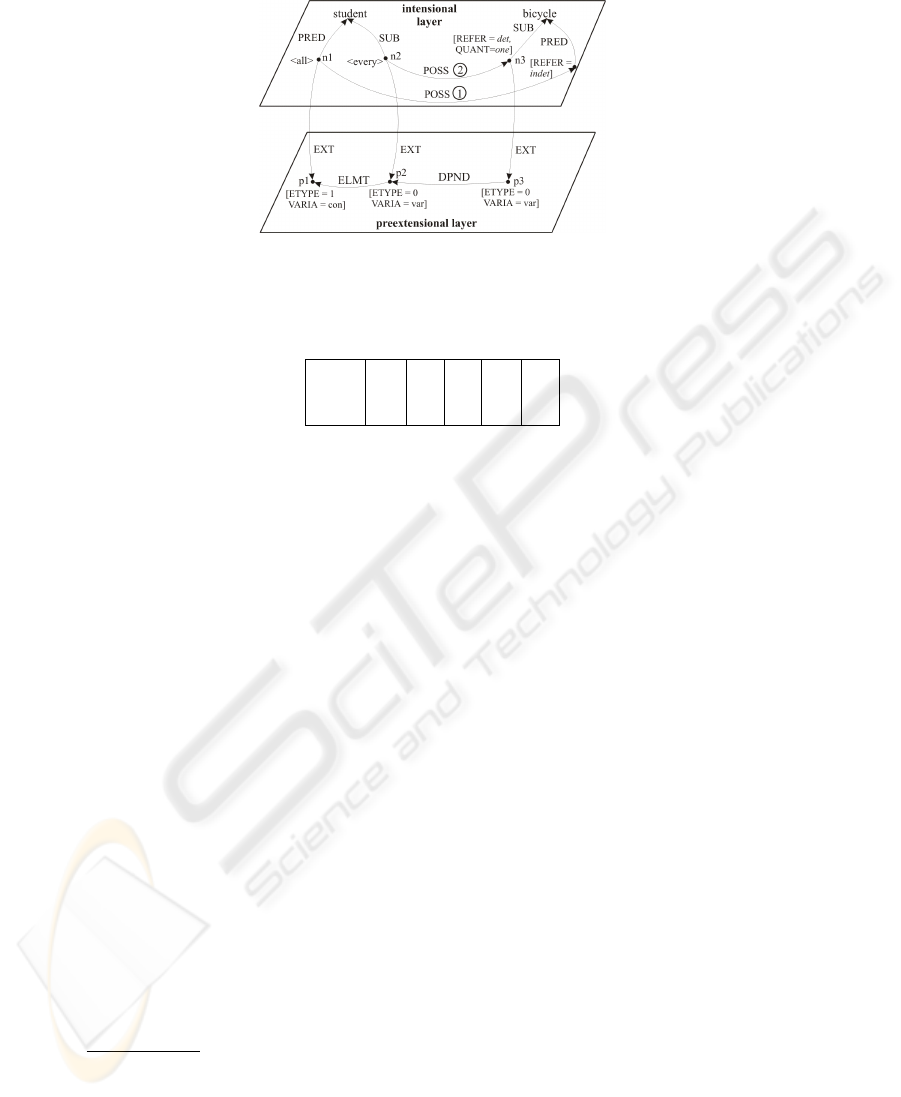
Fig. 3. Sample network with intensional and preextensional layers.

Table 3. Detail from the description of quantiﬁcators by means of layer attributes.

QUANT CARD VARIA REFER ETYPE

hall i all card con det +1

heveryi one 1 var det +0

pending on this student. Note that according to Table 3, n

has a non-varying collection

with determined reference as its extension, while n

and n

have varying extensions

with determined and indetermined references, respectively.

3 Intensional Quantiﬁcation and Preextensional Cardinality

The interplay of the intensional and extensional aspects of meaning becomes visible in

the linguistic phenomenon of intensional quantiﬁcation (carried by quantiﬁcators

“several”, “most”) and their extensional counterparts, the cardinalities of sets.

For the semantic representation of expressions containing these quantiﬁcators the

combination between the intensional and preextensional layer is needed (see motivating

example in introduction). Here we consider a similar case which demonstrates how the

example sentences are analyzed on the intensional and preextensional levels:

(S1) “Peter sent his mother many letters.” (Node sv

)

(S2) “Fife of them were lost.” (Arc sv

)

The MultiNet represented in Figure 4 reveals that sentence (S1) is indeed represented

on the intensional level only. The partitive construction in the second sentence, however,

requires a shift to the preextensional level. The representation of (S2) on the right-hand

side of the ﬁgure asserts that there is a conceptual node on the intensional level which

represents a plurality of lost letters. The extension of this node has cardinality 5. Since

the partitive “ﬁve of them” rather than “all of them” was used, we know that a proper

subset relationship holds between the set of lost letters and the letters Peter had sent to

his mother. We conclude that the set of sent letters has indeed more than 5 elements,

which conforms to the intuitive expectations.

To distinguish these constructs from the existential quantiﬁer ∃ and the universal quantiﬁer ∀

in logics, we deliberately coined the term “quantiﬁcator”.

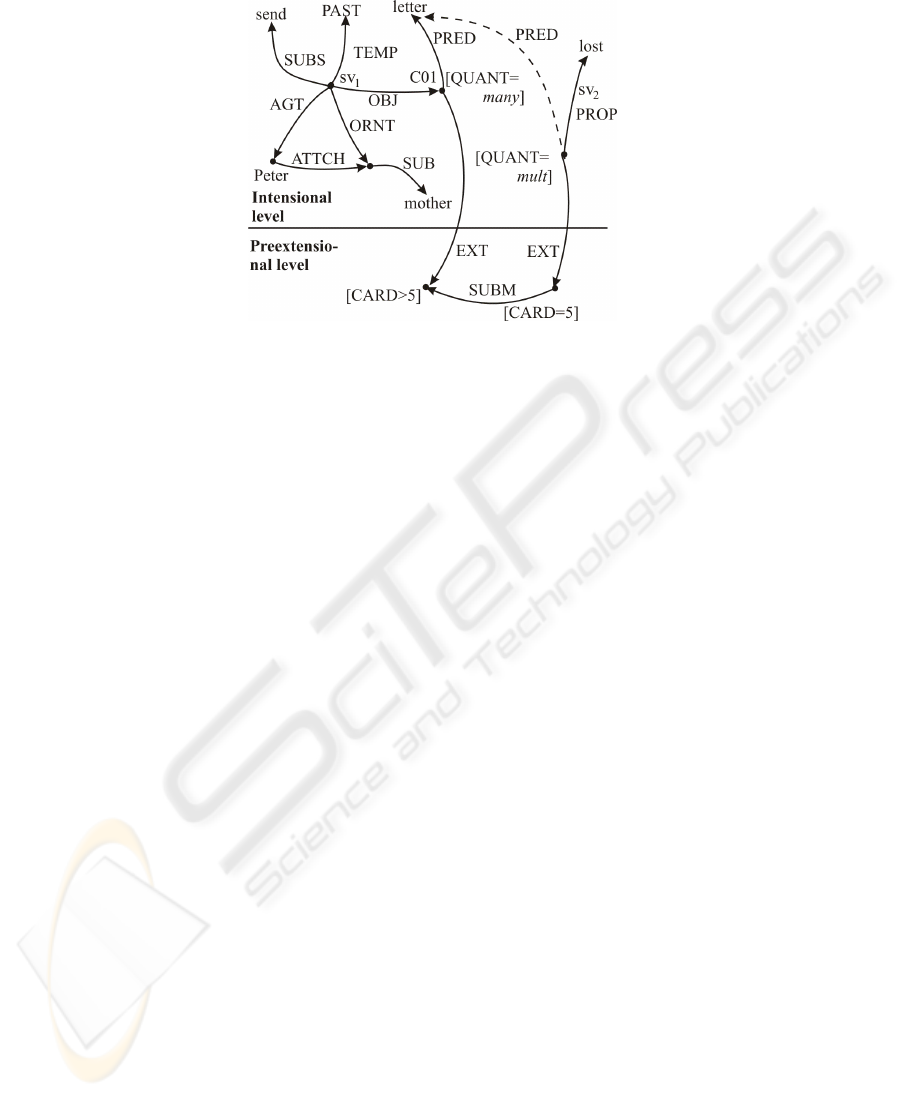
Fig. 4. Intensional quantiﬁcators vs. cardinalities on the preextensional level.

4 Different Types of Negation

The proper modeling of negation in a KRS is a difﬁcult task, since the usual negation

of ﬁrst-order logic does not cover all aspects of linguistic negation. Let us consider the

following example:

(N1) “The concert was not unpleasant.”

If we assume a constant c for the concrete concert and a unary predicate PLEASANT

for the meaning of the adjective “pleasant”, the typical way of expressing the meaning

of the above proposition in FOL would be: ¬¬PLEASANT(c), which is equivalent to

PLEASANT(c). However, PLEASANT(c) is clearly not the meaning of (N1), which

demonstrates that the law of double negation does not hold for this kind of negated

gradable properties. Notice that a degree-based modeling along the lines of [15] might

solve this problem on the theoretical side but only at the price of a very complicated

representation which is hardly suited for knowledge processing.

MultiNet offers two types of negation to deal with negated sentences. An intensional

negation of a state of affairs sv is expressed by a modal restriction (sv MODL *NON)

which corresponds to the negation contained in the sentence itself. But there is also

the preextensional negation of sv expressed by the layer attribute [FACT(sv)=nonreal]

saying that sv does not hold in reality. To see the rationale for discerning these two

kinds of negation, consider the problem of interpreting subordinated sentences intro-

duced by the conjunction “instead of ” in the case that the subordinated sentence again

involves negation. An example is “Instead of taking nothing from the table, the guest ate

everything up” which contains an intensional negation within the subordinated clause

by the negator “nothing”. This negation expressed by (sv

MODL *NON) in Figure 5

is the basis for answering a question aiming at the expectations of the dialogue partners

(“What did you expect?” – “That he took nothing!”) However the conjunction “instead

of ” introduces a second negation as a presupposition, which has to be represented by

[FACT=nonreal] with sv

, stating that the state of affairs which had been expected does

not hold in reality. If we mingled these two types of negation (intensional vs. preexten-

100

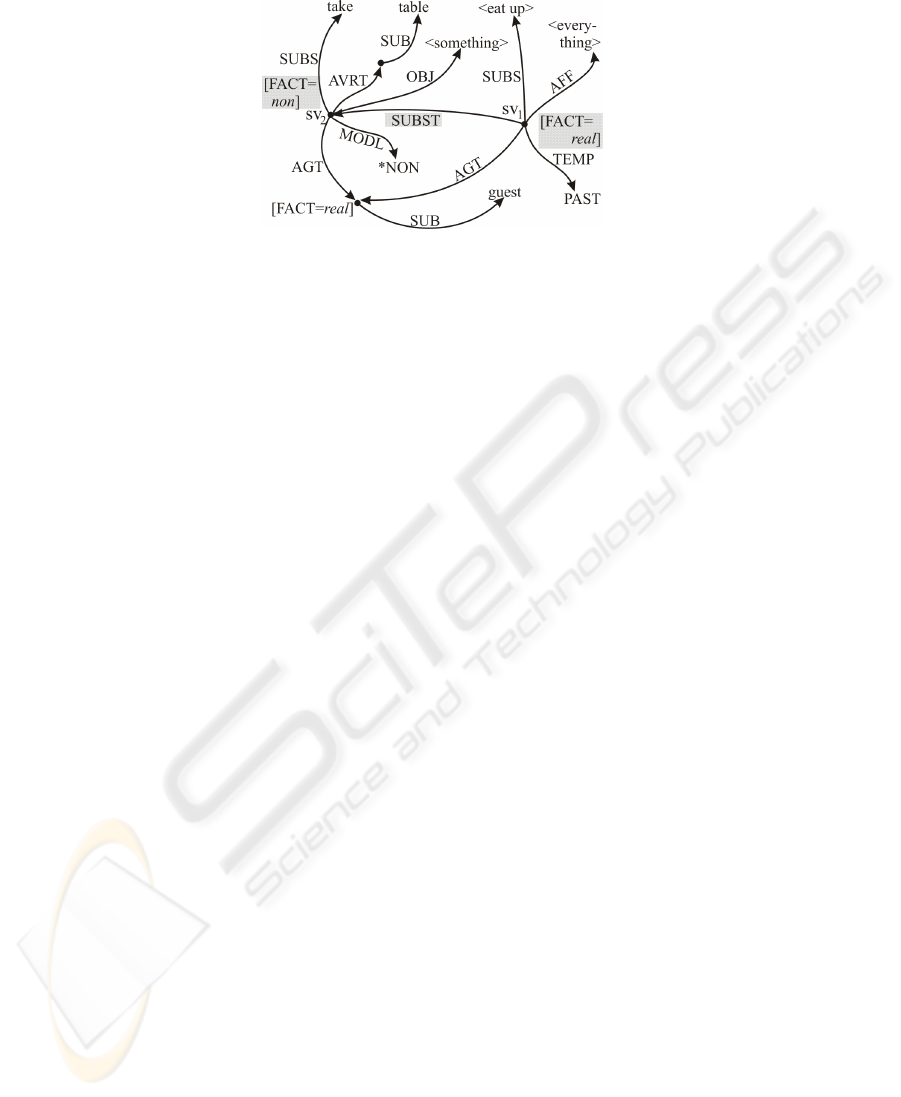
Fig. 5. The two types of negation in subordinated sentences.

sional) or even deleted both of them on the basis of a wrongly applied law of double

negation we could not answer the question asking for an expectation. However, the two

types of negation may obviously cancel out under certain circumstances. This would

be the case for questions with a purely factual character (“Did he take something from

the table?” – Answer: “Yes!”). In order to account for these effects, application of the

law of double negation (combining factual or preextensional negation with intensional

negation) should depend on the type of the question.

5 Existential Presuppositions and Counterfactuals

Another aspect of reference that must be captured by a KRS is concerned with the fac-

ticity of the entities of interest. In natural language we can discuss the existence or non-

existence of objects of a certain kind – like ghosts, aliens or black holes. It is also pos-

sible to talk about situations or events regardless of facticity. Consequently, [6, 7] em-

phasize the importance of modeling non-existing objects for knowledge representation.

In predicate logic, however, there is an inherent existence assumption for all individuals

(i.e. individual constants) because the model-theoretic semantics demands that all con-

stants denote in the universe. This is why we introduced the attribute FACT to express

the facticity of a considered entity. As opposed to certain dialects of modal predicate

logic which use an existence predicate to tell existing objects from non-existing ones

[5], we discern three possible cases, viz the real, nonreal and hypo as mentioned above.

The third value hypo is needed, for instance, to describe states of affairs in conditionals

or in opaque contexts. [8] argues that seven ways of existing should be distinguished,

which could easily be accomplished by extending the set of facticity values.

Table 4 shows some basic axioms related to facticity, which also express some of

the existential presuppositions made while uttering a factual statement. Axiom (a) states

that the agent or experiencer of a factual event/state must really exist. For example, Peter

can only know something if he is a real person. The same can also be said about LOC

and TEMP, i.e. a real situation takes place at a real location and has a temporal extent in

the real world. An exception to Axiom (a) is the MCONT role which expresses mental

content or modal embedding. Here, somebody’s belief in the existence of the Yeti is

classiﬁed hypo by axiom (b). However, as shown by (c), there are special cases (e.g.

knowing something) which license the conclusion that the second argument of MCONT

101

Table 4. Selected axioms related to facticity. Axioms marked by ∗ must be considered defaults.

(a) (x R x

) ∧ [FACT(x)=real] → [FACT(x

)=real]

where R ∈ {AFF, AGT, EXP, OBJ, . . . } (valid for most argument roles)

(b)

∗

(x MCONT x

) → [FACT(x

)=hypo]

) ∧ [FACT(s)=real] → [FACT(s

)=real]

(d) (x R x

) ∧ [FACT(x)=real] → [FACT(x

)=real]

where R ∈ {PARS, ELMT, HSIT} (for all meronymy relations)

(e) (s COND s

) → [FACT(s)=hypo] ∧ [FACT(s

)=hypo]

is factual as well. For that reason (b) was marked as default knowledge. Axiom (d) states

that a real aggregate can only be composed of real parts. Finally, Axiom (e) expresses

the observation that if-then-relationships involve hypothetical situations. Consider the

following example: “If John returns late, he will be tired.” In this case, there is obviously

no commitment as to the facticity of premise and conclusion, which are thus tagged

[FACT=hypo].

It should be pointed out that the FACT attribute allows us to model all types of

implicative verbs, factive verbs and counterfactive verbs as listed in the classiﬁcation of

[16]. We will pick two examples to demonstrate how to accomplish this.

The verb “forget to” is a so-called two-way implicative whose facticity pattern can

be described by the following two axioms:

(s SUBS hforget toi) ∧ (s MCONT m) ∧ [FACT(s)=real] → [FACT(m)=nonreal]

(s SUBS hforget toi) ∧ (s MCONT m) ∧ [FACT(s)=nonreal] → [FACT(m)=real] .

In other words, if Ed forgets to close the door, then Ed does not close the door; and if

Ed does not forget to close the door, then he actually closes the door.

Our second example is “forget that ”, a factive verb with a positive existential pre-

supposition. Here we only need one additional axiom to describe the facticity pattern:

(s SUBS hforget thati) ∧ (s OBJ m) ∧ [FACT(s)=nonreal] → [FACT(m)=real] .

Thus, if Ed does not forget that he closed the door, then Ed closed the door. Due to the

use of the OBJ role, the above axiom (a) already captures the opposite case, i.e. if Ed

forgets that he closed the door, we may conclude that Ed closed the door.

In practice, the entailments are expressed by axiom schemes for all verbs of the

considered type. In this way, all facticity patterns of [16] can be captured.

Counterfactuals are among the most prominent semantic phenomena where the

combination of intensional modality and preextensional facticity is needed to repre-

sent the full meaning. Figure 6 shows the proposed representation of the sentence: “If

the boy had come yesterday, he would have got the toy”. Our analysis of counterfactuals

introduces two pairs of situations which correspond to the upper and lower half of the

depicted MultiNet. There are two hypothetical situations ˜sv

and ˜sv

linked by a con-

ditional, expressing “If the boy came yesterday, he got the toy”. Moreover there is a pair

of negated factive situations with a causal relationship which roughly express “The boy

did not get the toy because he did not come yesterday.” These negated factive situations

and their causal link are implicit in the counterfactual statement.

102

Fig. 6. Representation of a counterfactual.

6 The Role of Extension Types in Semantic Representations

The extension type of concepts, introduced in Sect. 2.4 and represented by the layer

attribute ETYPE, is not only important for deﬁning the signatures of relations and

functions at the preextensional level (cf. Table 2). Combined with other expressional

means, it also explains the difference between quantiﬁed concepts as “all children”

with [ETYPE=1] and “every child” with [ETYPE=0] (cf. Figure 3). While expressions

of the ﬁrst type, when used in a sentence like “All children bought a gift”, allow for a

cumulative and a distributive reading (and, thus, need background knowledge for a fur-

ther interpretation), this is not the case for expressions with [ETYPE=0], as in “Every

child bought a gift”. The latter allows only for a distributive reading.

An effect seldom properly taken into account is the inﬂuence of the extension type

on the speciﬁcation of lexical meanings, especially in connection with the selectional

restrictions of verbs. Concepts underlying verbs like “die out” or verbal constructs like

“be at odds with each other” can only be used either in connection with concepts of

[ETYPE≥1] or possibly with generic concepts. Examples: “(The Miller clan)

[ETYPE=1]

died out.” – “(The Blue Whale)

[GENER=ge]

has almost died out.”

7 Partitive and Coordinating Quantiﬁcation

The last phenomenon to be discussed is the semantic interpretation of partitive and co-

ordinating quantiﬁers whose semantic representation requires the expressional means

of the preextensional layer. Partitive quantiﬁcations are typically expressed by prepo-

sitions like “beside/except”, “apart from”, “without”, and some uses of the preposition

“of ”. However, also coordinations building pluralities like “Some teachers and all stu-

dents” must refer to operations on sets which belong to the preextensional level. The

following example comprises typical effects in one sentence (N2):

“Many students and all teachers of the school except the director cleaned the room.”

Though such examples are routinely treated in the Theory of Generalized Quantiﬁers

[17], they are not visible in state-of-the art KRS. MultiNet, however, offers a corre-

sponding representation shown in Figure 7: To represent the meaning of sentence (N2)

and especially of the phrase “Many students and all teachers of the school except the

103

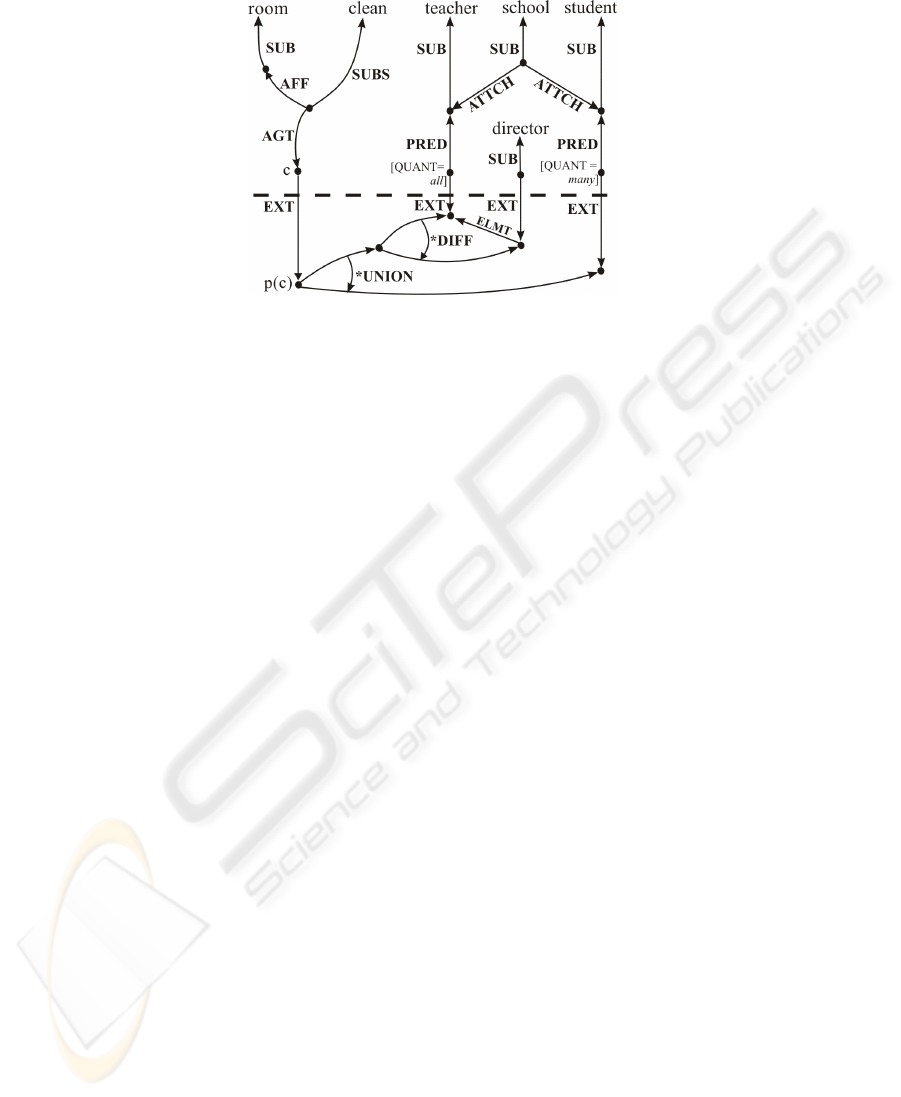
Fig. 7. The construction of pluralities by means of prepositions.

director ”, a concept c at the intensional level and its representative p(c) at the preexten-

sional level have to be created, which are related by (c EXT p(c)). For specifying p(c),

at ﬁrst a set difference is constructed using *DIFF to capture the meaning of “except”.

After that the union of the result with the set of many students has to be built using the

function *UNION to capture the effect of “and” on the coordinating quantiﬁcation.

8 Conclusion

We have argued that a comprehensive meaning representation for natural language ex-

pressions must combine the intensional and extensional aspects of semantic descrip-

tion. Since the full extension of a natural language concept is typically out of reach,

a preextensional layer was introduced which allows to deal with partially described

extensions or ‘preextensions’. Using Multilayered Extended Semantic Networks for se-

mantic representation, we discussed several linguistic phenomena whose interpretation

arguably involves the extensional aspect. We then explained how to handle theses cases

by combining the intensional and preextensional descriptive means of the framework.

Obviously there is specialized research into most of these issues (like handling par-

titive and coordinating quantiﬁcations or modeling facticity). However, none of these

approaches provides an integrated solution which has made its way into a working KRS.

The MultiNet approach, by contrast, has been used as a meaning representation formal-

ism in several projects (e.g. VirWiss [18]). It is also the semantic interlingua for repre-

senting user queries in natural language interfaces to internet information providers and

to local databases [19, 20]. Corresponding transformation modules exist which translate

MultiNet representations of questions into various target formats like Z39.50 and SQL.

The inference system of MultiNet and its axiom system are used in question answer-

ing (QA) systems [21, 22], in the natural language interfaces mentioned above, and in

the virtual electronic laboratory VILAB [23]. The use of MultiNet in the QA systems

InSicht and IRSAW is continually evaluated in the CLEF QA track (see [21, 22]) as

well as in the answer-validating system MAVE (AVE-track of CLEF [24]). In all CLEF

competitions from 2004 to 2006 these systems ranked among the best three for German.

104

References

1. Carnap, R.: Meaning and Necessity. Chicago University Press, Chicago (1947)

2. Janas, J.M., Schwind, C.B.: Extensional Semantic Networks. In Findler, N.V., ed.: Associa-

tive Networks. Academic Press (1979) 267–305

3. Brachman, R.J., Schmolze, J.G.: An overview of the KL-ONE knowledge representation

system. Cognitive Science 9 (1985) 171–216

4. Baader, F., Calvanese, D., McGuinness, D., Nardi, D., Patel-Schneider, P., eds.: The De-

scription Logics Handbook. Cambridge University Press, Cambridge (2004)

5. Lambert, K., ed.: Philosophical Applications of Free Logic. Oxford University Press (1991)

6. Hobbs, J.: Ontological promiscuity. In: Proc. 23rd Annual Meeting of the ACL. (1985)

7. Shapiro, S.C., Rapaport, W.J.: SNePS considered as a fully intensional propositional se-

mantic network. In Cercone, N., McCalla, G., eds.: The Knowledge Frontier: Essays in the

Representation of Knowledge. Springer, New York (1987) 262–315

8. Hirst, G.: Existence assumptions in knowledge representation. Artiﬁcial Intelligence 49

(1991) 199–242

9. Bobrow, D., Condoravdi, C., Crouch, R., de Paiva, V., Kaplan, R., Karttunen, L., King, T.,

Zaenen, A.: A basic logic for textual inference. In: Proceedings of the AAAI Workshop on

Inference for Textual Question Answering, Pittsburgh, PA (2005)

10. Helbig, H.: Knowledge Representation and the Semantics of Natural Language. Springer,

Berlin (2006)

11. Gnörlich, C.: Technologische Grundlagen der Wissensverwaltung für die automatische

Sprachverarbeitung. PhD thesis, FernUniversität Hagen, Hagen, Germany (2002)

12. Hartrumpf, S., Helbig, H., Osswald, R.: The semantically based computer lexicon HaGenLex

– Structure and technological environment. Traitement automatique des langues 44 (2003)

13. Helbig, H., Glöckner, I.: Reasoning over semantic networks - a typology of axioms for

natural language inference. In: Proc. MRCS-07, Hyderabad, India (2007) 30–34

14. Glöckner, I., Hartrumpf, S., Helbig, H.: Automatic knowledge acquisition by semantic anal-

ysis and assimilation of textual information. In: Proc. KONVENS 2006, Konstanz (2006)

15. Pulman, S.G.: Formal and computational semantics: a case study. In: Proc. 7th Int. Workshop

on Computational Semantics, Tilburg (2007) 181–196

16. Nairn, R., Condoravdi, C., Karttunen, L.: Computing relative polarity for textual inference.

In: Proceedings of ICoS-5 (Inference in Computational Semantics), Buxton, UK (2006)

17. Keenan, E., Moss, L.: Generalized quantiﬁers and expressive power of natural language. In

Benthem, J., Meulen, A., eds.: Generalized Quantiﬁers in Natural Language. Foris (1984)

18. Glöckner, I., Knoll, A.: Natural-language navigation in multimedia archives: An integrated

approach. In: Proc. 7th ACM Multimedia Conference (MM-99), Orlando, FL (1999)

19. Leveling, J., Helbig, H.: Das NLI-Z39.50 – Natürlichsprachliche Informationssuche zur

Verbesserung der Literaturrecherche. In: Proc. KONVENS 2006, Konstanz (2006) 97–100

20. Helbig, H., Gnörlich, C., Menke, D.: Realization of a user-friendly access to networked

information retrieval systems. Informatik-Bericht 196, FernUniversität Hagen (1996)

21. Hartrumpf, S.: Questio n answering using sentence parsing and semantic network matching.

In: Working Notes for the CLEF 2004 Workshop, Bath, England (2004) 385–392

22. Leveling, J.: A baseline for NLP in domain-speciﬁc information retrieval. In: Accessing

Multilingual Information Repositories (Proc. CLEF-05). LNCS-4022. Springer (2006)

23. Lütticke, R., Gnörlich, C., Helbig, H.: VILAB - a virtual electronic laboratory for applied

computer science. In: Proc. Conf. Networked Learning in a Global Environment. (2002)

24. Glöckner, I.: University of Hagen at QA@CLEF 2006: Answer validation exercise. In Nardi,

A., Peters, C., Vicedo, J.L., eds.: Working Notes for the CLEF 2006 Workshop. (2006)

105